唯一分解整环R上的多项式环R[x]

卢梦霞，凡美金，赵廷芳

(周口师范学院 数学与统计学院,河南 周口 466001)



唯一分解整环R上的多项式环R[x]

卢梦霞，凡美金，赵廷芳

(周口师范学院 数学与统计学院,河南 周口 466001)

主要从三个方面来讨论唯一分解整环R上的多项式环R[x].首先，讨论了唯一分解整环R和R[x]的内在联系；其次，讨论了Q[x]中的元素f(x)的可约性；最后，讨论了R[x]中的元素f(x)的根和f(x)表达式中系数的关系.

唯一分解整环；商域；本原多项式；单位

1　预备知识

设R是唯一分解整环，R[x]是R上的一个多项式环.

定义1[1]R[x]中的元素f(x)是一个本原多项式.假如f(x)的系数的最大公因式是单位.

引理1[1]如果R[x]的一个非零多项式f(x)在Q[x]里能分解成两个次数较低的多项式的乘积，则f(x)一定能在R[x]里分解成两个次数较低的多项式的乘积.

引理2[2]一个整环是唯一分解整环的充分必要条件是：

(1)R中任意序列a1,a2,…,an,…,

其中每一个ai+1都是ai的真因子(i=1,2,…)只能含有限项.

(2)R中每一个可约元都是素元.

2　主要结论

定理1[3]环R是唯一分解整环，当且仅当R[x]也是唯一分解整环.

证 必要性:见参考文献[4].

充分性:设f1(x),f2(x),…,fn(x),…,是一个真因子序列，如果元素个数是无限的话.

令gn(x)是fn(x)的一个本原多项式因子，于是存在dn∈R，使得

fn(x)=dngn(x)n=1,2,…

fn(x)=dngn(x)=qn+1(x)fn+1(x)=

由此可得

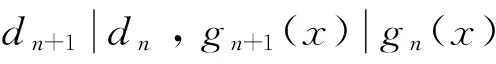
因R是唯一分解整环，可知存在正整数k，使得dn～dn+1.当n≥k时，于是由

∂(gk(x))>∂(gk+1(x))>…

此为不可能，故因子的序列只能是有限的.

设p(x)是可约多项式.

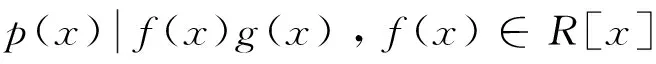
d(x)=q1(x)p(x)+

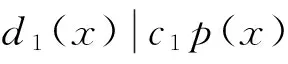
若d1(x)是R[x]的一个单位，则d1(x)是零次多项式d(x)∈R，进而知d(x)g(x)=q1(x)p(x)g(x)+q2(x)f(x)g(x)

定理2 设R是唯一分解整环，R[x]是环R上关于未定元x的多项式环,设f(x)∈R[x]，令f(x)=a2n+1x2n+1+…+a0，若有一个素数p使得

p3⫮a0,p⫮a2n+1

则f(x)在Q[x]里是不可约的，其中Q是R的一个商域.

证 若f(x)在Q[x]里可约，则f(x)可以分解成R[x]的两个次数较低的多项式的乘积，令

f(x)=(btxt+…+b0)(cmxm+…+c0)

(t,m<2n+1,t+m=2n+1).

总之，f(x)都不能有形如f(x)=(blxl+…+b0)(cmxm+…+c0)的分解式，即f(x)在Q上不可约.

[1]王高峡．唯一分解整环上的一元多项式环的因子分解[J]．湖北三峡学院学报，1999,21(5)：12-14．

[2]杨传箴，徐先珍，许心正．唯一分解整环上的多项式环[J]．黑龙江大学自然科学学报，1989(1)：10-12．

[3]卢梦霞，凡美金，赵廷芳．几种整环之间的探讨[J]．周口师范学院学报，2015,32(5):34-35．

[4]郭世乐．整环上的一元多项式环[J]．福建师范大学福清分校学报，2004(2)：3-4．

Polynomial ring R[x] of unique factorization domain R

LU Mengxia,FAN Meijin, ZHAO tingfang

(School of Mathematics and Statistics, Zhoukou Normal University, Zhoukou 466001,China )

The properties of the polynomial ring R[x] of the ring R have been described in detail in many textbooks and papers. This paper mainly discusses the polynomial ring R[x] of the unique factorization domain Rfrom three aspects. First, the paper discusses the inner link between unique factorization domain R and R[x].Secondly, the paper discusses the reducibility of element f(x) in Q[x].Finally, the paper discusses the relationship between the roots of element f(x)in Q[x] and the coefficients of f(x) expression.

unique factorization domain; quotient domain; primitive polynomial; unit

2016-04-04;

2016-05-01

周口师范学院教学改革项目(No.J201215)

卢梦霞(1975- )，女，河南太康人，副教授，硕士，主要从事概率及代数学的教学与研究.

O153.3

A

1671-9476(2016)05-055-02

10.13450/j.cnki.jzknu.2016.05.014