广义余扭曲余代数的性质

刘红江

(河南应用技术职业学院 基础教学部,河南 郑州 450042)



广义余扭曲余代数的性质

刘红江

(河南应用技术职业学院 基础教学部,河南 郑州 450042)

利用对偶的思想,由广义扭曲代数的性质给出了广义余扭曲余代数的一些相关性质.

余扭曲子;余代数映射;余模

1　预备知识

代数结构和余代数结构是Hopf代数研究的主要内容，而在此研究过程中经常用到对偶的思想方法,该方法可以由已知的代数结构及其性质得到余代数的相关结论.近年来，人们得到了许多代数结构和余代数结构的推广形式，并给出了它们的性质[1-3].文献[4]引入了扭曲子的概念, 利用它得到了一种新的代数结构,即广义扭曲代数,同时讨论了广义扭曲代数的性质.该代数结构是广义Smash积的推广形式. 利用对偶思想,文献[5]引入了余扭曲子的概念, 并利用余扭曲子得到了一种新的余代数结构-广义余扭曲余代数，从而推广了广义Smash余积的概念. 笔者将讨论广义余扭曲余代数的性质.

定理1[3]设C和D是余代数,线性映射W:C⊗D→D⊗C是余扭曲映射,则下列条件是等价的.

(1)CW⊗D是广义Smash余积.

(2)下面条件成立

(ID⊗εC)·W(c⊗d)=εC(c)d

(εD⊗IC)·W(c⊗d)=εD(d)c

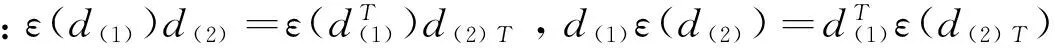
T12·T13·Δ2=Δ2·T:D⊗D→D⊗D⊗D,T23·T13·Δ1=Δ1·T:D⊗D→D⊗D⊗D,T23·T12=T12·T23:D⊗D⊗D→D⊗D⊗D,其中Δi,i=1,2,表示对第i个元素作用,则双线性映射T·Δ:D→D⊗D是定义在D上的另一个余结合余代数结构,余单位是εD,把它表示为DT,映射T叫做D的余扭曲子.

2　主要结果及其证明

定理3设S是余代数D的一个余扭曲子,U是余代数F的一个余扭曲子，如果V:D→F是余代数映射，使得(V⊗V)·S=U·(V⊗V),那么V:DS→FU是余代数映射.

证要证V:DS→FU是余代数映射,即证：

U·ΔF·V=(V⊗V)·S·ΔD,εF·V=εD

已知V:D→F是余代数映射,所以

ΔF·V=(V⊗V)·ΔD,εF·V=εD

又因为(V⊗V)·S=U·(V⊗V),所以

U·ΔF·V=U·(V⊗V)·ΔD=(V⊗V)·S·ΔD

定理得证.

该例就是定理3的一个特殊例子,其中D=B⊗A,F=B'⊗A',V=g⊗f,S(U)是从W(W')得到的余扭曲子.

定理4设(D,Δ,ε)是余代数,S:D⊗D→D⊗D是D的余扭曲子,则有下列结论

(1)设V是左D-余模,λ:V→D⊗V,λ(v)=v(-1)⊗v(0).假设Γ:D⊗V→D⊗V是已给定的线性映射,Γ(d⊗v)=dΓ⊗vΓ,d∈D,v∈V,使得：

ε(v(-1)Γ)v(0)Γ=ε(v(-1))v(0)

和

S12·Γ13·λ2=λ2·Γ:D⊗V→D⊗D⊗V

S12·Γ23·Γ13·Δ=Δ·Γ:D⊗V→D⊗D⊗VS12·Γ23=Γ23·S12:D⊗D⊗V→D⊗D⊗V

那么V成为左DS-余模,Γ·λ:V→D⊗V ,VΓ是V上的左DS-余模结构,Γ·λ(v)=v(-1)Γ⊗v(0)Γ.称映射Γ为V的相对于S的左余模余扭曲子.

(2)设V是右D-余模,ρ:V→V⊗D,ρ(v)=v(0)⊗v(1).假设Π:V⊗D→V⊗D是已给定的线性映射,Π(v⊗d)=vΠ⊗dΠ,d∈D,v∈V ,使得：

v(0)Πε(v(1)Π)=v(0)ε(v(1))

和

S23·Π12·Π13·Δ=Δ·Π:V⊗D→V⊗D⊗D,S23·Π13·ρ=ρ·Π:V⊗D→V⊗D⊗D,

Π12·S23=S23·Π12:V⊗D⊗D→V⊗D⊗D,那么V成为右DS-余模,Π·ρ:V→V⊗D ,V上的右DS-余模结构用VΠ来表示，Π·ρ(v)=v(0)Π⊗v(1)Π，称映射Π为V的相对于S的右余模余扭曲子.

(3)设V是D-双余模,Γ,Π是V的相对于S的左、右余模余扭曲子,VΓ是左DS-余模和VΠ是右DS-余模.假设下面条件满足：

Γ12·ρ=ρ·Γ:D⊗V→D⊗V⊗D,

Π23·λ=λ·Π:V⊗D→V⊗D⊗D,

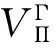
证(1)要证V是左DS-余模,只需证

ε(v(-1)Γ)v(0)Γ=v,

v(-1)Γ⊗(v(0)Γ)(-1)Γ'⊗(v(0)Γ)(0)Γ'=

(v(-1)Γ)1⊗(v(-1)Γ)2⊗v(0)Γ,

所以, (v(-1)Γ)1⊗(v(-1)Γ)2⊗v(0)Γ=

((v(-1)1)Γ)S⊗(v(-1)2)Γ'S⊗v(0)ΓΓ'=

((v(-1))Γ)S⊗(v0(-1))Γ'S⊗v0(0)ΓΓ'=

((v(-1))Γ)S⊗(v0(-1))SΓ'⊗v0(0)ΓΓ'=

v(-1)Γ⊗(v(0)Γ)(-1)Γ'⊗(v(0)Γ)(0)Γ'

而ε(v(-1)Γ)v(0)Γ=v显然是成立的.

(2)要证V是右DS-余模,需证

v(-1)Πε(v(0)Π)=v

(v(0)Π)(0)Π'⊗(v(0)Π)(1)Π'⊗v(1)Π=

v(0)Π⊗(v(1)Π)1⊗(v(1)Π)2

由V是右D-余模,可知

v(0)ε(v(1))=v,

v(0)(0)⊗v(0)(1)⊗v(1)=v(0)⊗v(1)1⊗v(1)2,

所以 v(0)Π⊗(v(1)Π)1⊗(v(1)Π)2=

v(0)ΠΠ'⊗((v(1)1)Π')S⊗(v(1)2)ΠS=

v(0)(0)ΠΠ'⊗((v(0)(1))Π')S⊗(v(1))ΠS=

v(0)(0)ΠΠ'⊗((v(0)(1))S)Π'⊗(v(1))ΠS=

(v(0)Π)(0)Π'⊗(v(0)Π)(1)Π'⊗v(1)Π

v(-1)Πε(v(0)Π)=v显然成立.

(3)由V是D-双余模可知

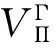
v(-1)Γ⊗(v(0)Γ)(0)Π⊗(v(0)Γ)(1)Π=

v(0)Π(-1)Γ⊗(v(0)Π)(0)Γ⊗v(1)Π

因为,v(-1)Γ⊗(v(0)Γ)(0)Π⊗(v(0)Γ)(1)Π=

v(-1)Γ⊗(v(0)(0))ΓΠ⊗(v(0)(1))ΓΠ=

v(0)(-1)Γ⊗(v(0)(0))ΓΠ⊗(v(1))ΓΠ=

v(0)(-1)Γ⊗(v(0)(0))ΠΓ⊗(v(1))ΠΓ=

v(0)Π(-1)Γ⊗(v(0)Π)(0)Γ⊗v(1)Π

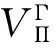
[1] ME Sweedler. Hopf algebras[M]. New York: W.A.Benjamin Inc, 1969.

[2] C Kassel. Quantum groups[M]. New York: Springer-Verlag, 2000.

[3] S Caenepeel, Bogdan lon, G Military, et al. The factorization problem and the smash biproduct of algebras and coalgebras[J]. Algebras and Representation Theory,2000, 3(1): 19-42.

[4] Javier L P, F Panaite, F V Oystaeyen. General twisting of algebras[J]. Advances in Mathematics, 2007, 212(1): 315-337.

[5] 焦争鸣,刘红江.广义扭曲双代数[J].河南师范大学学报(自然科学版), 2011, 39(2): 10-12,16.

The properties of generalized cotwisted coalgebras

LIU Hongjiang

(Henan Vocational College of Applied Technology, Basic Teaching Department,Zhengzhou 450042, China)

Using the ideas of duality and the properties of the generalized twisted algebras,we give some properties of the generalized cotwisted coalgebra.

cotwistor; coalgebra mapping; comodule

2016-03-25;

2016-05-15

刘红江(1982- ),男，河南郑州人,硕士，讲师, 研究方向: Hopf代数和量子群.

O153.3

A

1671-9476(2016)05-0053-02

10.13450/j.cnki.jzknu.2016.05.013