ARIMA模型在人口序列预测中的应用

顾翠伶,王　宁

(周口师范学院 数学与统计学院,河南 周口 466001)



ARIMA模型在人口序列预测中的应用

顾翠伶,王宁

(周口师范学院 数学与统计学院,河南 周口 466001)

对1990-2014年中国人口数据序列进行实证分析．利用1990-2013年的数据建立ARIMA(0,1,1)模型、ARIMA(1,1,1)模型、ARIMA(1,1,0)模型，以AIC准则为选择标准，得出ARIMA(0,1,1)模型为最优的模型．通过该模型对2014年的人口数进行预测，求得模型的预测精度很高．最后对1990-2014年的人口数建立ARIMA(0,1,1)模型，得到未来几年的人口预测值，结果表明中国人口将呈现持续增长的趋势．

ARIMA模型；Eviews；预测

中国是一个人口大国,但在经济上却是发展中国家.人口众多与社会资源的相对有限,形成了一对尖锐的矛盾，为了更好地协调和解决这一矛盾，对人口序列进行分析、预测有很重要的意义.同时人口预测研究是国家制定未来人口发展目标和生育政策等有关人口政策的基础,对国民经济计划的制定和社会战略目标的实现有重要的参考价值[1].人口时间序列预测是根据一个历史的序列观测值,找出符合人口变化规律的函数,根据这个函数将历史观测值作为输入值,预测出未来的人口值.本文对1990-2014年中国人口时间序列进行分析，建立ARIMA模型，对未来人口数进行分析，为相关政策的制定提供依据．

1　预备知识

1.1单位根检验

单位根检验是检验时间序列平稳性的一种方法，是1979年Dickey和Fuller提出的，简称ADF.原假设H0：该时间序列存在单位根，即序列非平稳.备择假设H1：该时间序列不存在单位根，即序列平稳.若ADF的检验值大于给出的单位根检验的临界值，那么接受假设H0，认为该时间序列存在单位根；反之，ADF的检验值小于临界值，接受假设H1，可认为该时间序列不存在单位根，是平稳序列.

1.2差分

对于非平稳的时间序列，可以进行差分运算处理，使其变成平稳的时间序列．一阶差分为Xt=Xt-Xt-1=(1-B)Xt，若差分处理后的时间序列仍是非平稳的，则需进行二次差分.则二阶差分为2Xt=[(Xt-Xt-1)-(Xt-1-Xt-2)]=(1-B)2Xt.差分运算的实质是以自回归方式提取序列中的确定性信息．

1.3ARIMA模型

ARIMA模型的实质就是差分与ARMA模型的组合，而ARMA模型是一种常用的精度很高的时序短期预测方法，只适用平稳序列，对于非平稳序列，就要通过适当阶数的差分将非平稳序列变成平稳，然后对差分后的平稳序列进行ARMA(p,q)模型拟合，即ARIMA模型.ARIMA模型的基本思想是将随时间推移而形成的数据序列视为一个随机序列，即除去个别的因偶然原因引起的观测值外，时间序列就是对随机过程进行观测所取得的一组离散观测.这组随机变量的单个序列值虽然具有不确定性，但对整个时间序列来说，它的变化却有一定的规律性，可以用相应的数学模型来近似描述.通过对该数学模型的分析研究，能够更清晰地认识时间序列的结论与特征，达到最小方差意义下的最优预测.

具有如下结构的模型称为求和自回归移动平均模型,简记为ARIMA(p,d,q)模型[2]

(1)

Φ(B)=1-φ1B1-φ2B2-…-φpBp为平稳可逆ARMA(p,q)模型的自回归系数多项式，

Θ(B)=1-θ1B1-θ2B2-…-θqBq为平稳可逆ARMA(p,q)模型的移动平滑系数多项式，

1.4ARIMA模型的建模过程

①当获得观察值序列之后，对时间序列进行平稳性检验，常用的方法为图示法及单位根检验法；

②若时间序列是非平稳的，则可以经过差分运算，将其转化为平稳时间序列；

③对差分后的序列建立ARMA(p,q)模型；

④对所建立的模型进行检验；

⑤利用通过检验的模型进行序列的预测．

2　建立ARIMA模型对中国人口序列进行预测

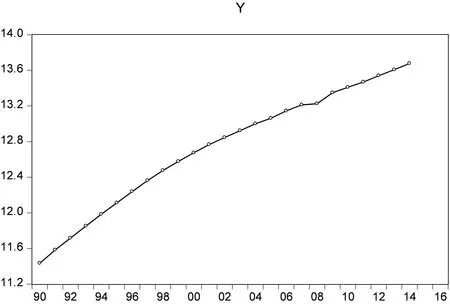
图2人口序列一阶差分时序图

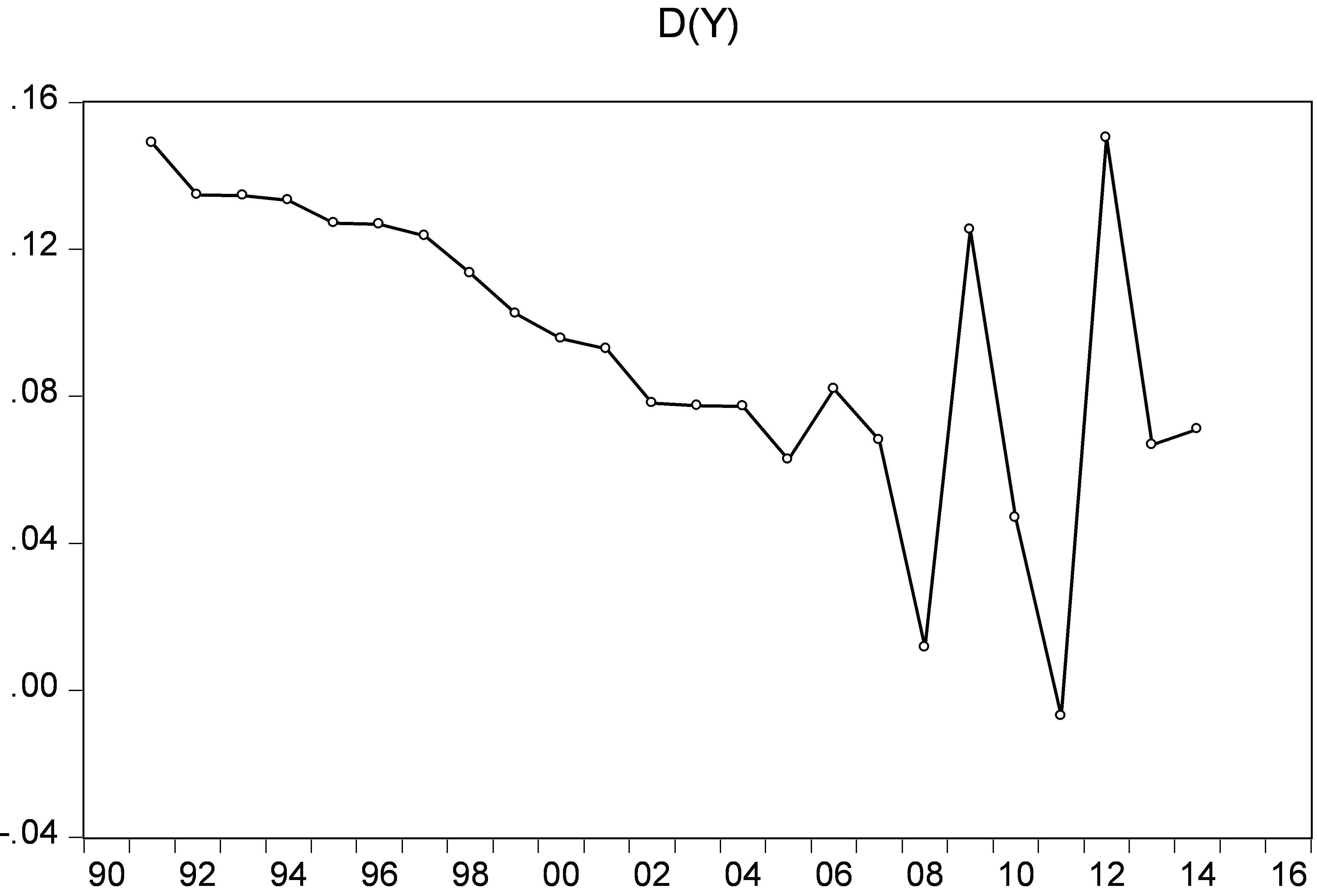
图2人口序列一阶差分时序图

表1　原始序列与一阶差分序列的单位根检验

图3给出了该一阶差分序列的自相关与偏自相关图，从图中可以看出，该序列为非白噪声序列．对平稳的非白噪声序列，可以建立ARIMA模型进行拟合，选择三种模型进行估计，估计的结果如表2所示．由图2知，ARIMA(0,1,1)模型的AIC值最小，因而ARIMA(0,1,1)模型在三个模型中拟合效果最好.对ARIMA(0,1,1)模型的残差进行分析，由图4及5可以看出：ARIMA(0,1,1)模型的残差序列为白噪声序列，该模型通过残差检验．

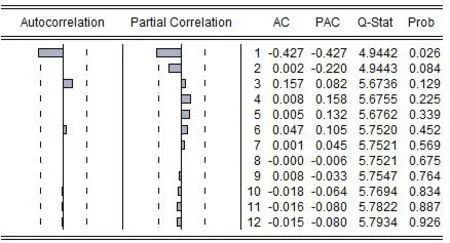
图3一阶差分序列的自相关与偏自相关图

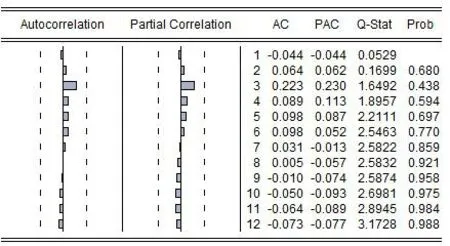
图4ARIMA(0,1,1)残差序列自相关与偏自相关图

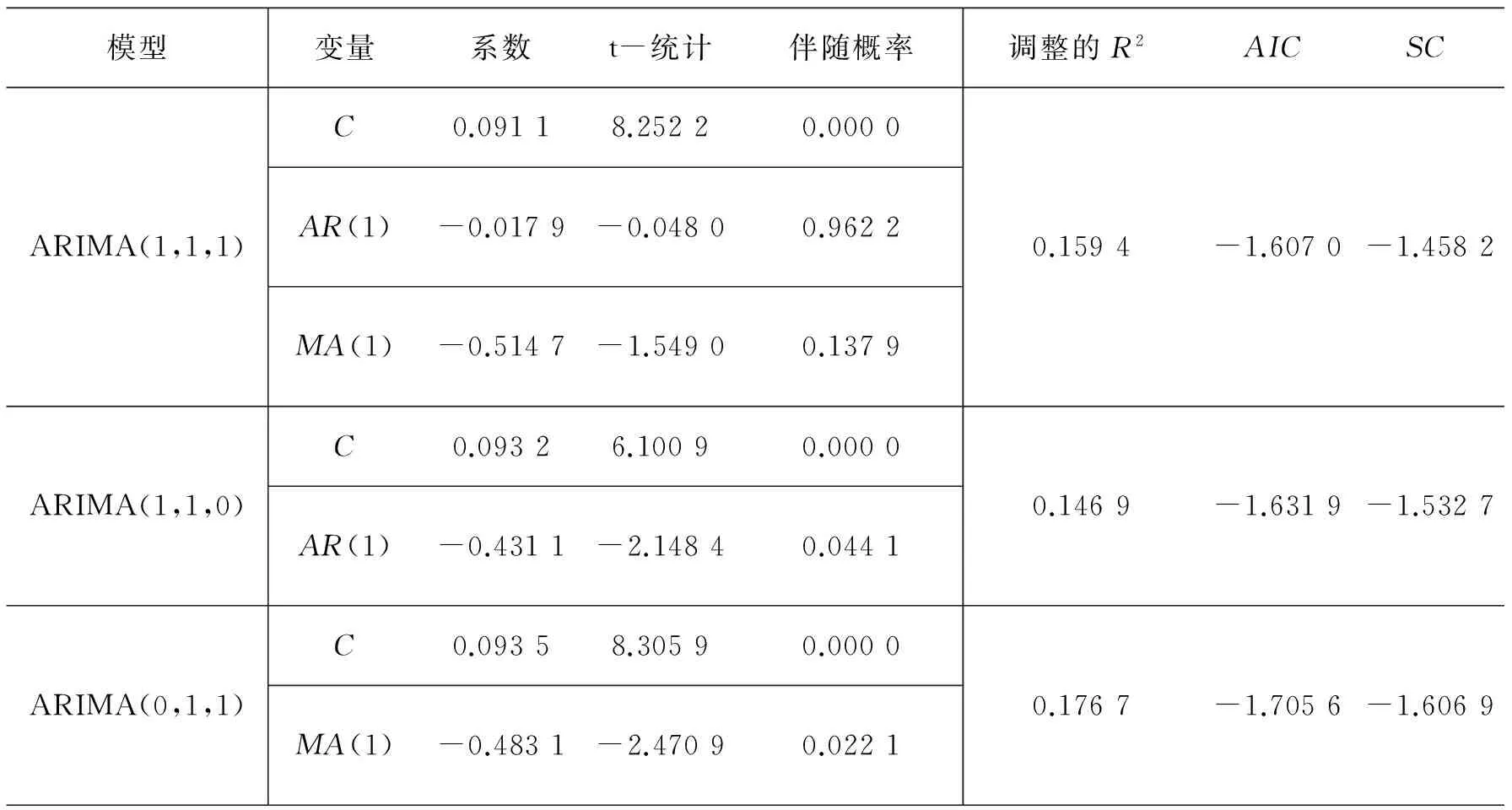
表2　三种ARIMA模型的估计结果及比较

表3　ARIMA(0,1,1)模型的预测值

3　总结

ARIMA模型使用差分的方式提取确定性信息，差分方法的优点是对确定性信息的提取比较充分，笔者对1990-2014年中国人口时间序列进行分析，建立ARIMA模型，对未来人口数进行分析，结论合理．

[1] 吴劲军.基于BP神经网络的人口预测模型研究[J].统计与决策,2004,171(3):4-5.

[2]王黎明,王连,杨楠.应用时间序列分析[M].上海：复旦大学出版社,2009.

ARIMA model application in prediction of population

GU Cuiling,WANG Ning

(Mathematics and Statistical Institute, Zhoukou Normal University, Zhoukou 466001,China)

Empirical analysis was employed on population data of China from 1990 to 2014.Firstly,ARIMA (0,1,1) model、ARIMA (1, 0) model and ARIMA (1,1,1) model were established by using the data from 1990-2013. the AIC criterion be used to select the optimal model. it is concluded that ARIMA (0,1,1) model for the best model. Through this model to forecast the population of 2014 and we obtained high prediction precision of the model. Finally, established the model of ARIMA (0,1,1) based on the population of 1990-2014 and forecast the number of the next few years. The results show that China's population will continue to grow.

ARIMA model; Eviews; forecast

2015-07-03;

2015-09-12

顾翠伶(1986- ),女,河南项城人，助教,硕士,主要研究方向:统计分析.

C924.2

A

1671-9476(2016)05-050-03

10.13450/j.cnki.jzknu.2016.05.012