混合效应模型线性估计的可容许性

高继梅，梁艳艳

(周口师范学院 数学与统计学院，河南 周口 466001)



混合效应模型线性估计的可容许性

高继梅，梁艳艳

(周口师范学院 数学与统计学院，河南 周口 466001)

以协方差矩阵和Kronecker乘积为基础，建立混合效应模型的线性可容许性的必要条件，简化固定效应和随机效应的估计.在平衡套分类模型场合简化线性估计的容许性问题，给出其固定和随机效应线性估计可容许的充要条件.

Kronecker乘积；混合效应模型；可容许

关于线性模型的可容许性问题，统计判决理论中已有很多经典结果，1976年，Olsen，Seely和Birkes利用局部最优估计来刻画可容许的线性无偏估计[1]，1982年LaMotte发展了他的思想方法, 提出了一个研究线性模型中线性估计可容许性的一般理论方法，但是对于具体的线性模型，用那些方法刻画具体的线性估计的可容许性也不是容易的[2].1988年，叶慈南针对具有两个方差分量的模型, 研究了方差分量的非负二次同时估计的可容许性，在一定的条件下给出了一个充分条件和一个必要条件,但是必要条件非常苛刻，关于可容许性估计的刻画很不理想[3].笔者在这一点做出了突破，在没有参数约束的情况下，给出了混合效应模型，特别是平衡交叉分类模型的可容许性条件，推广和发展了混合效应模型参数估计的容许性条件.

1　混合效应模型的预备知识

线性混合效应模型是最重要的一种常见回归模型，它的最一般形式为

y=Xβ+U1ξ1+U2ξ2+…+Ukξk+e

(1)

y为观测向量，X为已知设计阵，β为非随机的参数向量，称为固定效应，Ui为已知设计阵，ξi为随机向量，称为随机效应，ei为随机误差向量[4].一般假设

Y=Xβ+ZU+e

(2)

(3)

(4)

(5)

2　 混合效应模型的改进

由以上结果可知：

(6)

由上式可以得到LTY-KTXβ=LTY-θ

因此，可以把风险函数LTY看作模型(6)中KTXβ的估计，此时LTY看起来只含固定效应而不含随机效应了[7].

3　交叉分类模型的线性可容许性

引理1关于θ的一个线性估计LTY在模型(3)中是可容许的，当且仅当其相应的KTXβ的估计LTY在模型(6)中是可容许的.

在这里,考虑K—平衡交叉分类随机模型的线性可容许性，它们是模型(3)的特殊情况.通过研究得到模型(6)中KTXβ的可容许线性估计的明确公式，并且通过引理1，可以得到一个对于模型(3)的可容许线性估计.

令Yi1i2...ik+1，K—平衡交叉分类随机模型是一个具有下列结构的随机变量

Yi1i2...ik+1=β+u1i1+...+ukik+ei1i2...ik+1，

在这些假定下，将Yi1i2...ik+1按字典排序法排成一个n—维向量Y，这里n=n1,n2,...,nk+1.令X=In1⊗In2⊗...⊗Ink+1=In,Znk=In1⊗In2⊗...⊗Ik⊗1nk+1.这时，相对于模型(3)，此模型有[9]

(7)

⋮

⋮

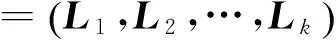
即有

ML0=s0XXTK

(8)

ML*-AQ=0

(9)

由式(8)得：

L0=s0M-1XXTK

(10)

由式(9)得：

(11)

又因为是Ei幂等正交阵，所以有

[1]A. Olsen, J. Seely, D. Birkes. Invariant quadratic unbiased estimation for two variance components[J]. Ann. Statist,1976,4:878-890.

[2]L. R. LaMotte. Admissibility in linear estimation[J]. Ann. Statist,1982,10: 245-255.

[3]叶慈南. 两个方差分量同时估计的可容许性[J]. 应用概率统计,1988,4(1):35-43.

[4]王松桂,史建红,吴密霞，等,线性模型引论[M].北京:科学出版社,2003: 256-267

[5]庄东辰,茆诗松. 混合系数线性模型的参数估计[J]. 应用概率统计,1996,11(1):81-87.

[6]薛蕊,郭大伟. 线性混合模型中参数估计的容许性[J]. 杭州师范大学学报(自然科学版),2010,9(1):26-29.

[7]段智力. 约束下线性混合模型参数估计的渐近解及其收敛性[J]. 数学的实践与认识,2012,42(4):186-194.

[8]陈长生,徐勇勇,王彤. 交叉设计资料的混合效应模型分析[J]. 中国卫生统计,2005,22(4):214-217.

[9]徐宏武. 幂等矩阵的性质及应用[J]. 宜春学院学报,2004,26(6):22-22.

The admissibility of the linear estimate in mixed-effect model

GAO Jimei,LIANG Yanyan

(Mathematics and Statistical Institute, Zhoukou Normal University, Zhoukou 466001, China)

Based on covariance matrix and Kronecker product, necessary admissibility of mixed-effect model is established, and estimations of fixed effect and random effect are simplified. Furthermore, permissibility of linear estimation is simplified in balance set model, and permissibility of its fixed effect and random effect is given.

Kronecker product; mixed-effect model; permissibility

2016-05-03;

2016-05-20

高继梅(1964- )，女，河南淮阳人，硕士，副教授，主要研究方向：概率统计及应用.

F830

A

1671-9476(2016)05-0021-05

10.13450/j.cnki.jzknu.2016.05.005