变时滞脉冲下时滞神经网络的稳定性

白丹莹

(重庆师范大学 数学学院，重庆 401331)



变时滞脉冲下时滞神经网络的稳定性

白丹莹

(重庆师范大学 数学学院，重庆 401331)

对时滞神经网络的全局稳定性进行研究，施加一个与系统状态有关的时滞脉冲控制，通过B-等价系统将对变时滞神经网络的稳定性研究等价为对相对应的定时滞神经网络稳定性的研究.

变时滞脉冲；时滞神经网络；全局指数稳定；B-等价系统

时滞神经网络是神经网络的一个重要组成部分，它的动力学问题引起了学术界的广泛关注.时滞脉冲系统有定时脉冲系统和变时滞脉冲系统.变时滞脉冲与系统的状态有关，因此相对于定时脉冲来说研究上有一定的困难.目前，定时脉冲系统已有大量的研究[1-3]，而变时滞脉冲系统的研究则相对较少[4-6].在现有的刊物中，大部分用比较系统的方法来研究变时滞脉冲系统的稳定性[5-6].文献[7]研究了具有可变脉冲时刻的脉冲微分方程的稳定性理论的比较原则.文献[8]运用脉冲微分方程的比较原理建立了极值的解决方案，得到了脉冲微分方程的稳定性结果.在文献[9]中，作者利用比较原理和上下解的概念对具有脉冲变量的微分方程进行研究并取得结果.在文献[10]中，作者用比较原则研究了具有脉冲微分方程的应用，即扩展非牛顿流体的稳定流动.

1　问题陈述和预备知识

(1)

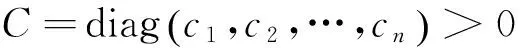
定义1[4]给定一个函数V，Rn→R+，若V在区域∑上，则满足

(2)V对x满足局部lipschitzian条件.

引理[7]设X，Y是具有适当维数的实矩阵，ε是正常数，则有

2XTYεXTX+ε-1YTY.

2　基本条件和B-等价系统

给出如下假设条件：

可以得到：

(2)

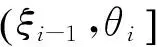
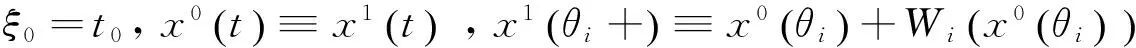
注意：系统(1)的B-等价系统是一个定时脉冲系统.系统(2)的稳定性表明变时脉冲系统(1)具有相同的稳定性.

3　变时滞脉冲系统的稳定性分析

定理1给定一个正定矩阵P，常数α>0，θ1>0，θ2>0,

那么系统(1)全局指数稳定.

当t≠ξk，

当t=ξk，

得证.

4　数值模拟

考虑如下脉冲系统：

(3)

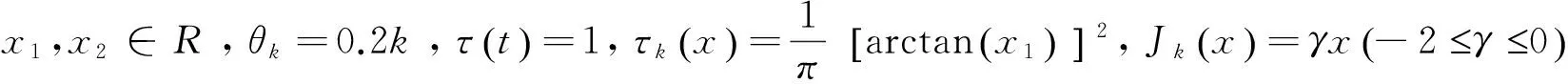
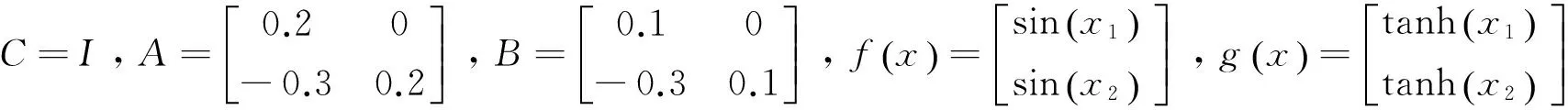
且有

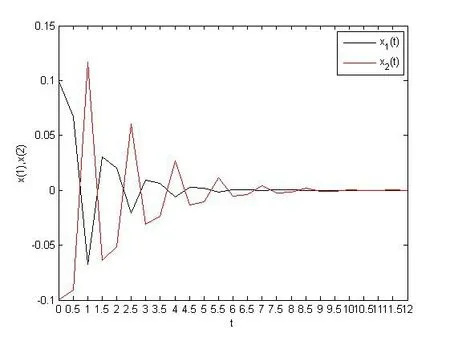
图1　系统的稳定曲线，x(0)=[0.1,-0.1]T.

5　结论

变时滞脉冲控制可以等价为相对应的固定时刻脉冲控制，则变时滞神经网络系统也可以等价为相对应的定时滞神经网络系统来研究.本文通过B-等价系统对带变时滞脉冲的时滞神经网络系统进行转化，通过研究相对的带定时脉冲的时滞神经网络系统的稳定性来确定变时滞神经网络系统的稳定性，且通过数值验证成立.

[1] Guan ZhiHong, Lam James, Chen Guanrong.On impulsive auto-associative neural Networks[J].Neural Networks,2000,13(1):63-69.

[2] Guan ZhiHong, Lam James, Chen Guanrong.On delayed impulsive Hopfield neural Networks[J].Neural Networks,1999,12(2):273-280.

[3]A.Arbi,C.Aouiti,F.Cherif,et al.Stability analysis of delayed HOPFIELD NEURAL NETWORKS with impulsive via inequality techniques[J].NEUROCOMPUTING,2015,158:281-294.

[4] T. Yang. Impulsive ControlTheory[M]. Springer-Verlag: berlin, 2001.

[5] V. Lakshmikantham, D. D. Bainov, P.S. Simeonov. Theory of impulsive differential Equations[M]. Singaproe:World Science,1989.

[6] V.Lakshmikantham,S.Kaul.Comparison principle for impulsive differential equations with variable times and Stability theory[J]. Nonlinear Anal. Theory Appl,1994，22(4): 499-503.

[7] Petersen I R. A stabilization algorithm for a class of uncertain linear systems[J]. Systems&Control Letters,1987,8(4):351-357.

[8] S. Leela Kaul, V. Lakshmikantham, S. Kaul. Extremal solutions, comparison principle and stability criteria for impulsive differential equations with variable times[J]. Nonlinear Anal,1994,22(10):1263-1270.

[9] M. Frigon,D.O’Regan.Impulsive differential equations with variable times[J].Nonlinear Anal.,1996,22(12):1913-1922.

[10] X. L. Fu, J. G. Qi, Y. S. Liu. General comparison principle with variable times differential equations with application[J]. Nonlinear Analysis,2000,42(8):1421-1429.

Stability of delayed neural networks with variable time impulsive control

BAI Danying

((College of Mathematics Sciences Chongqing Normal University,Chongqing 401331,China)

This paper addresses the problem of stability for delayed neural networks, applied a system state and the time delayed impulsive control. We shall show the variable time impulsive delayed neural networks can reduce to the case of fixed time impulses via B-equivalence method. Then we can by the study of the stability of the variable time impulsive delayed neural networks to change to the corresponding fixed time impulses delayed neural networks stability study.

variable time impulse; delayed neural network; global exponential stability; B-equivalence

2016-04-07;

2016-05-17

国家自然科学基金(No.61302180)

白丹莹(1995- )，女，河南邓州人，研究生，研究方向为脉冲控制与动力系统.

O29

A

1671-9476(2016)05-0016-05

10.13450/j.cnki.jzknu.2016.05.004