基于ELMD的样本熵及Boosting-SVM的滚动轴承故障诊断

何志坚 ， 周志雄

(1. 湖南大学 机械与运载工程学院，长沙　410082； 2. 湖南信息职业技术学院，长沙　410282)



基于ELMD的样本熵及Boosting-SVM的滚动轴承故障诊断

何志坚1，2， 周志雄1

(1. 湖南大学 机械与运载工程学院，长沙410082； 2. 湖南信息职业技术学院，长沙410282)

针对滚动轴承非平稳性的振动信号，提出了基于总体局域均值分解(Ensemble Local Mean Decomposition, ELMD)的样本熵及Boost-SVM的滚动轴承故障诊断法。首先，对振动信号进行ELMD分解，获得一系列乘积函数(Product Function, PF)；其次，根据分解特性提出基于K-L散度的自适应法选取主PF分量，计算主PF分量的样本熵并将其组合成特征向量；最后，将特征向量输入Boosting-SVM分类器进行训练与测试，从而识别滚动轴承的故障类型。实验结果表明，该方法能够有效的诊断出三种状态，且效果较局域均值分解法好。

滚动轴承；故障诊断；总体局域均值分解；样本熵

滚动轴承广泛应用于航天航空、冶金工业等重要设备领域，然而，由于工作条件恶劣导致轴承常常发生损坏[1-3]。因此，研究滚动轴承故障诊断对保证机械设备安全运行具有重要意义。

由于滚动轴承故障振动信号具有非平稳特性，因此有必要采用非平稳信号处理方法对其进行分析。SMITH等[4-6]提出了一种新的非平稳信号处理方法——局域均值分解(Local Mean Decomposition, LMD)，它可以将一个非平稳信号自适应的分解为若干调频调幅信号。LMD法自提出后在脑电、机械故障诊断等领域获得广泛应用，然而，与EMD(Empirial Mode Decomposition)法一样，LMD分解过程中也存在模态混叠现象，严重的模态混叠将导致时频分布混叠，进而产生物理意义不明确的PF(Product Function)分量，为此，提出利用白噪声具有频率分布均匀的特性来解决模态混叠问题，即总体局部均值分解法[7-8]。样本熵是衡量信号复杂度的一种新方法，由于抗噪能力强、处理数据长度要求不高等特点而被广泛应用于脑电、心电、机械故障诊断等领域，为此，文中引入样本熵表征滚动轴承的故障特征。

本文首先对振动信号进行总体局域均值分解，根据分解特性提出基于K-L散度的自适应法提取主PF分量，计算主PF分量的样本熵，取多组不同工作状态的样本熵组成特征向量输入Boosting-SVM分类器进行故障识别。实验结果表明，该方法对滚动轴承故障状态能够有效识别。

1　LMD及ELMD(Ensemble LMD)方法原理

1.1LMD基本原理

局域均值分解是将振动信号分解为若干由不同尺度的包络信号和纯调频信号乘积得到的PF分量，分解后PF分量可以写成如下形式：

PF1(t)=a1(t)s1(t)

(1)

式中：a1(t)为PF分量的包络信号;s1(t)为PF分量的纯调频信号。

对纯调频信号处理获得PF分量的瞬时频率：

(2)

将PF分量从原始信号中逐渐分离出来,最后得到残余分量uk(t)，原始信号X(t)可以写成k个PF分量和残余分量之和：

(3)

1.2ELMD方法原理

总体局部均值分解是一种改进的局部均值分解方法，该方法利用白噪声具有频率分布均匀的统计特性来解决模态混叠问题[9-10]。它将有限幅值的白噪声加入泄漏信号中形成混合信号进行多次LMD分解，且每次加入不同的白噪声，最后将多次分解得到的多个PF分量进行总体平均，其总体平均值作为最终的分解结果，由于白噪声的均值为零，所以取多次分解结果的平均值可以自动剔除加入的白噪声成分。基于以上原理，ELMD的具体步骤如下：

(1) 将白噪声加入振动信号中形成混合信号。

(2) 对混合信号进行LMD分解，获得多个PF分量。

(3) 重复步骤(1)和步骤(2)，但是每次都加入不同的白噪声信号。

(4) 将多次分解的多个PF分量进行总体平均，之后将平均值作为最终的分解结果。

1.3算法仿真及分析

冲击是机械故障振动信号中常见模式，因此，将冲击成分加入正弦信号形成混合信号，将此混合信号作为仿真信号进行分解(见图1)。

图1　仿真信号及组成成分Fig.1　The simulation signal

分别采用LMD及ELMD对仿真信号进行分解，用ELMD对仿真信号处理时，加入噪声幅值为信号标准差的0.01倍，总平均次数为100次，结果(见图2和图3)。

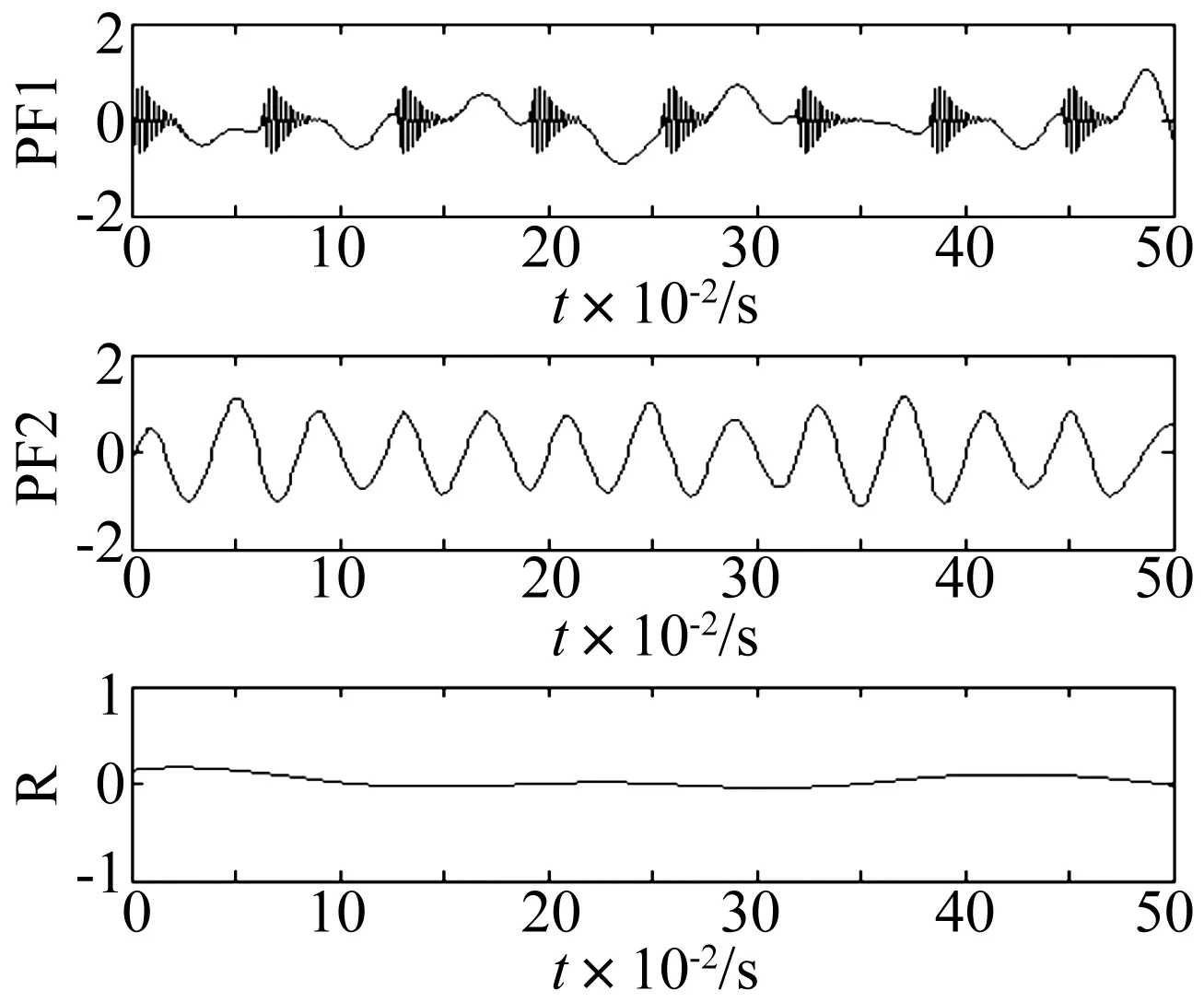
图2　仿真信号经LMD分解结果Fig.2　LMD decomposition result of simulation signal

图3　仿真信号ELMD分解结果Fig.3　ELMD results of simulated signal

由图2可知，仿真信号LMD分解过程中存在模态混叠现象，PF1分量和PF2分量中都有正弦成分，无法获得准确的PF分量；观察图3，仿真信号经ELMD分解后，前两个PF分量分别对应仿真信号中的冲击信号及正弦信号，隐藏在仿真信号的两个成分被较好的分解出来，由此可见，ELMD能够有效的消除LMD分解过程中存在的模态混叠现象。

2　提取故障特征

2.1K-L散度自适应法

对振动信号进行ELMD分解获得到多个PF分量，有些PF分量是与故障紧密相关的分量，而其他的PF分量则与故障无关或者是噪声干扰成分，因此有必要对PF分量进行处理，将包含故障主要特征的PF分量提取出来。研究表明K-L散度可用于衡量两个信号之间的相似度，散度值越小表明信号之间的相似度越高，反之，相似度越低[11-12]，为此提出K-L散度自适应算法提取主要PF分量，去除虚假分量。基于K-L散度的自适应算法步骤如下：

(1) 对于信号x=[x1,x2，…，xn]和信号y=[y1,y2，…，yn]，采用非参数估计法计算概率分布：

(4)

(5)

式中:x的概率分布为p(x)，同理对信号Y进行处理，求出概率分布为q(x)，h为给定的正数。

(2) 依据两信号的概率分布分别计算K-L距离。

(6)

按照以上公式计算信号X的K-L距离为δ(p,q)，同理信号Y的K-L距离为δ(q,p)。

(3) 计算两信号的K-L散度值

D(p,q)=δ(q,p)+δ(p,q)

(7)

D(p,q)为两信号X和Y的散度值。

(4) 计算阈值λ，将散度值小于λ的作为主PF分量。

λ=max(D(PFi,x))/ε,i=1,2,3,…

(8)

经过多次实验，式中ε取值为15，D(PFi,x)为分解的PF分量与原信号的K-L散度值。

2.2样本熵

样本熵是一种与近似熵类似但精度更好的度量信号复杂度的方法[13-14]。对于任意序列{x(i)|1≤i≤N}，其计算步骤如下：

(1) 给定模式维数，利用原序列形成m维矢量x(i)。

x(i)=(x(i),x(i+1),…,x(i+m-1))

i=1,2,…,N-m+1

(9)

(2) 定义矢量x(i)与x(j)之间的距离。

(10)

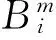
(11)

式中:i,j=1,2,…,N-m+1,i≠j，对所有的i进行平均值，得到Bm(r)。

(12)

(4) 对维数m进行加1，重复步骤(1)～步骤(3)，获得Bm+1(r)。

(5) 由以上理论可得此序列的样本熵为：

(13)

若N取有限值，那么此序列长度为N时的样本熵的估计值为：

(14)

3　Boosting-SVM分类器

Boosting-SVM分类器是在SVM的基础上，通过算法自动加权融合形成的一种新型强分类器，该分类器不仅具有在解决小样本方面的优越性，还适用于数据集多样化的情况[15]。滚动轴承发生故障是一个渐变的过程，提取的特征往往具有多样性，单一的通过特征值辨识故障存在一定的难度，因此，文中采用Boosting-SVM分类器对滚动轴承的故障进行识别，消除多样化的影响。对于n个带标签的样本{(x1,y1),(x2,y2),…,(xn,yn)}，xi为样本特征向量，yi(yi∈{+1,-1})为对应标签，w(i)为n个样本权重，初始样本权值为w(i)=1/n，迭代次数为m。其算法步骤为：

(1) 依据样本分布，利用SVM得到弱分类器

hj=p(x,y,w)

(15)

(2) 计算弱分类器hj的分类误差

(16)

(3) 根据分类误差调整样本的权重

aj=(1/2)ln[(1-Eerr)/Eerr]

(17)

(4) 依据权重大小，对样本分布进行调整

(18)

Zj是归一化系数，若此次得到的样本分布和上次相同，则退出，否则继续循环。

(5) 获得预测函数

(19)

弱分类器h=(h1,h2,…,hT)，权重a=(a1,a2,…,aT)。

Boosting-SVM分类器采用线性C-SVM分类器作为基本弱分类器，通过弱分类器对轴承的不同工作状态进行识别，根据分类误差调整样本权重，然后依据权重大小进行加权融合，最终实现强分类器。

4　实验分析

4.1实验情况简介

实验数据采用美国Case Western Reserve University的滚动轴承数据，将型号为SKF6205的深沟球轴承的驱动端轴承作为测试轴承，实验中由人工采用电火花机在轴承内、外圈加工制作形成轴承局部损伤，并将传感器安装在电动机输出支撑轴承上端机壳上进行测量。实验中轴承损点直径为0.017 8 cm，转速为1 797 r/min,采样频率为12 kHz,每个数据样本长度N为3 000点，实验采集装置见图4，采集的三种振动信号见图5。

图4　实验采集装置Fig.4　Apparatus & procedures

图5　传感器采集的三种振动信号Fig.5　Three collected signals by sensors

以外圈故障信号为例，由于篇幅所限，对采集的信号进行ELMD分解，结果见图6。

图6　外圈故障信号ELMD分解结果Fig.6　ELMD of outer fault signal

由图6可知，外圈故障信号经ELMD分解获得7个PF分量，不同的PF分量反映了信号中不同的特征成分。按照上文所述K-L散度自适应法计算PF分量与原信号的K-L散度值，结果见表1。

表1　 PF分量与原信号的K-L散度值

根据式(8)计算阈值λ，得出振动信号阈值依次为0.038 45，0.039 1，0.035 7。根据阈值选出主PF分量，正常信号的主PF分量为PF1、PF2和PF3；内圈故障信号的主PF分量为PF1、PF2、PF3；外圈故障信号的主PF分量为PF1、PF2、PF3。利用主PF分量重构原振动信号，分别计算原信号与重构信号的均方差和能量，结果见表2。

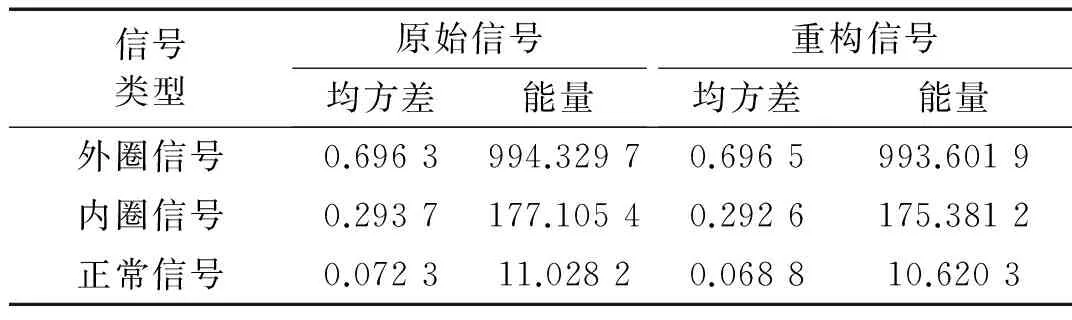
表2　原始信号及重构后信号的均方差及能量

由表2可知，对主要PF分量进行重构，计算重构前后信号的特征统计量，可以发现原始信号和重构信号的特征统计量相近，说明K-L散度自适应法能够有效的获得主要PF分量。

4.2计算主PF分量的样本熵

分别计算不同状态的主PF分量的样本熵，经过多次试验，m=1,r=0.2时不同状态的样本熵区分较明显。取多组不同工作状态的样本熵值进行平均，结果见表3。

表3　 三种类型信号前三个PF分量的样本熵

由表3可知，样本熵可以用来表示振动信号的复杂程度，熵值越大，其振动信号越复杂。正常状态的轴承振动信号振动平稳，复杂度低，因此熵值最小，由于内圈信号离传感器距离较远，采集的振动信号有噪声干扰，因此熵值较外圈故障信号大。为了对此，分别采用ELMD和LMD对信号进行分解，计算PF1分量的样本熵，其结果见图7。

图7　经LMD和ELMD分解的PF1样本熵Fig.7　The sample entropy of the PF1 component by ELMD and LMD

由图7可知，由于LMD分中存在模态混叠的问题，因此LMD分解过程中产生物理意义不明确的PF分量，导致振动信号经LMD分解后的样本熵分布不均匀，且区别不明显，ELMD方法克服了模态混叠的问题，分解后的PF1分量的样本熵区别较明显。为了进一步对滚动轴承故障进行识别，文中采用Boosting-SVM对其状态进行精确识别。

4.3故障识别

分别计算不同状态的样本熵值，取多组数据组成特征向量输入Boosting-SVM分类器进行训练与测试。为了对比，分别采用支持向量机、BP神经网络分类器，识别结果见图8。

由图8可知，随着训练组数的增加，识别率越来越高；本文提出的分类器能够有效的对不同工作状态进行识别，且识别率高于BP及SVM分类器。

5　结　论

滚动轴承发生故障时，针对复杂振动信号，本文提出一种基于ELMD、样本熵特征提取及改进SVM的复合故障诊断方法，并得出如下结论：

图8　三种分类器的不同识别率Fig.8　The classification accuracy of the three methods on different signals

(1) 采用ELMD方法对振动信号进行分解，能够有效的克服模态混叠现象，获取准确的PF分量；在此基础上通过分析PF分量与原信号之间的相似度提出基于K-L散度的自适应选择算法，去除虚假分量。

(2) 采用改进的SVM分类器对不同故障进行识别，结果表明该分类器能够有效的识别不同的工作状态,且识别率较SVM及BP高。

[1] LEI Y G, ZUO M J. Fault diagnosis of rotating machinery using an improved HHT based on EEMD and sensitive IMFs [J]. Measurement Science and Technology, 2009, 20(12):1-12.

[2] 隋文涛，张丹，WILSON Wang.基于EMD和MKD的滚动轴承故障诊断[J].振动与冲击，2015，34(9):55-59.

SUI Wentao, ZHANG Dan,WILSON Wang. Fault diagnosis of rolling element bearings based on EMD and MKD [J]. Journal of Vibration and Shock, 2015, 34(9):55-59.

[3] 冯毅，曹劲然，路宝春，等. 基于连续峭度优化的滚动轴承故障特征提取小波变换方法[J].振动与冲击，2015，34(14):27-32.

FENG Yi,CAO Jinran, LU Baochun, et al. Fault feature extraction method for rolling bearing based on wavelet transform optimized by continuous kurtosis [J]. Journal of Vibration and Shock, 2015, 34(14):27-32.

[4] SMITH J S. The local mean decomposition and its application to EEG perception data [J]. Journal of the Royal Society, 2005, 2(5):443-454.

[5] SUN J D, XIAO Q Y, WEN J T, et al. Natural gas pipeline small leakage feature extraction and recognition based on LMD envelope spectrum entropy and SVM [J]. Measurement, 2014, 55(9):434-443.

[6] FENG Z P, ZUO M J, QU J, et al. Joint amplitude and frequency demodulation analysis based on local mean decomposition for fault diagnosis of planetary gearboxes [J]. Mechanical Systems and Signal Processing,2013,40(1):56-75.

[7] SUN J D, XIAO Q Y, WEN J T, et al. Natural gas leak location with K-L divergence-based adaptive selection of ensemble local mean decomposition components and high-order ambiguity function [J]. Journal of Sound and Vibration, 2015, 347:232-245.

[8] LEI Y G, HE Z J, ZI Y Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery [J]. Mechanical Systems and Signal Processing, 2009, 23(4):1327-1338.

[9] 周智，张优云，朱永生，等．基于EEMD 和共振解调的滚动轴承自适应故障诊断[J]．振动与冲击，2013，32(2):76-80.

ZHOU Zhi, ZHANG Youyun, ZHU Yongsheng, et al.Adaptive fault diagnosis of rolling bearings based on EEMD and demodulated resonance [J]. Journal of Shock and Vibration, 2013, 32(2):76-80.

[10] WU Z H, HUANG N E. A study of the characteristics of white noise using the empirical mode decomposition method [J]. Proceedings of the Royal Society of London．Series A: Mathematical, Physical and Engineering Sciences, 2004(460):1597-1611.

[11] ZHANG F, LIU Y, CHEN C, et al. Fault diagnosis of rotating machinery based on kernel density estimation and Kullback-Leibler divergence [J]. Journal of Mechanical Science and Technology, 2014, 11(28):4441-4454.

[12] SHAPOVALOV M V, DUNBRACK R L. A smoothed backbone-dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions[J]. Structure, 2011, 19(6): 844-858.

[13] 苏文胜，王奉涛，朱泓，等. 基于小波包样本熵的滚动轴承故障特征提取[J]. 振动、测试与诊断，2011，31(2):162-166.

SU Wensheng, WANG Fengtao, ZHU Hong, et al. Feature extraction of rolling element bearing fault using wavelet packet sample entropy[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(2):162-166.

[14] RICHMAN J S, MOORMAN R J. Physiological time-series analysis using approximate entropy and sample entropy [J]. American Journal of & Physiol Heart & Circ Physiol, 2000, 278(6):2039-2049.

[15] WANG C W, YOU W H. Boosting-SVM: effective learning with reduced data dimension [J]. Applied Intelligence, 2013, 39(3):465-474.

Fault diagnosis of roller bearings based on ELMD sample entropy and Boosting-SVM

HE Zhijian1,2, ZHOU Zhixiong1

(1. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China;2. Hunan College of Information, Changsha 410082, China)

Aiming at the non stationary characteristics of a gear fault vibration signal, a recognition method was proposed based on the sample entropy of ELMD (ensemble local mean decomposition) and Boosting-SVM. The vibration signal was decomposed by ELMD, and a series of product functions (PFs) were obtained. According to the decomposition characteristics of ELMD, an adaptive method based on K-L divergence was proposed to select out the principal PFs. The sample entropies of principal PF components were calculated and combined into a feature vector, which was then input in a Boosting-SVM classifier to train and test for identifying the type of roller bearing faults. The experimental results show that the method can effectively diagnosis three kinds of working conditions and the effect is better than the local mean decomposition method.

roller bearing; fault diagnosis; ensemble local mean decomposition; sample entropy

国家科技重大专项资助项目(2012ZX04003041);国家自然科学基金资助项目(51475158)

2015-08-11修改稿收到日期：2015-09-23

何志坚 男，博士生，1974年生

周志雄 男，教授，博士生导师，1953年生

TP206

A DOI:10.13465/j.cnki.jvs.2016.14.031