一类Euler函数方程的解的上界

谢自珍，蒋卓玲，何海霞，黄美玲

(阿坝师范学院数学与财经系，四川 汶川 623000)



一类Euler函数方程的解的上界

谢自珍，蒋卓玲，何海霞，黄美玲

(阿坝师范学院数学与财经系，四川 汶川 623000)

设φ(n)为正整数n的Euler函数，讨论了Euler函数方程φ(x1…xn-1xn)=m(φ(x1)+…+φ(xn-1)+φ(xn))的求解问题，给出了该方程的所有正整数解的较为精确的上界.作为应用，对于一些给定的正整数m和n，求出了此时方程的全部正整数解.

Euler函数；函数方程；正整数解；解的上界

【引用格式】谢自珍，蒋卓玲，何海霞，等.一类Euler函数方程的解的上界[J].北华大学学报(自然科学版)，2016，17(5)：577-580.

1 引言及主要结论

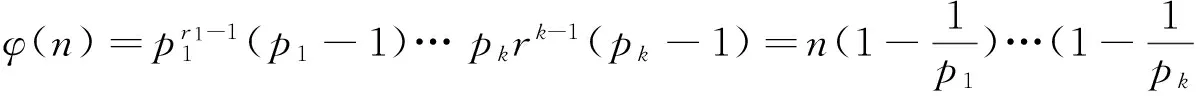
长期以来，Euler函数的性质一直是数论中引人关注的研究课题[1-2].对于Euler函数方程φ(x)=m以及φ(x)=φ(x+k)的解，PErdös，AMakowski，Schinzel，KFord等著名学者做过大量的研究[3-10].

文献[11]讨论了方程φ(ab)=k(φ(a)+φ(b))的解问题，给出了该方程整数解的一些结论；文献[12]讨论了方程φ(abc)=2(φ(a)+φ(b)+φ(c))，并求出了该方程的全部正整数解.随后，文献[13-16]均讨论了与Euler函数相关的类似方程的解，用初等数论的方法获得了这些函数方程的所有解.设 m和n是给定的正整数，文献[17]讨论了更一般的函数方程

φ(x1…xn-1xn)=m(φ(x1)+…+φ(xn-1)+φ(xn))

(1)

的求解问题，证明了其正整数解数的有限性.

本文进一步讨论方程(1)的解，根据Euler函数φ(n)的性质，在文献[17]的基础上，利用与之相似的方法，给出方程(1)的所有正整数解的更为精确上界，证明了：

定理1 当n≥3，m≥2时，方程(1)的所有正整数解(x1≤…≤xn-1≤xn)满足

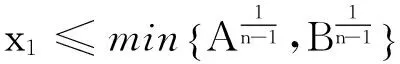
(2)

xn≤min{2.6m2n(n-1)ln(m2n(n-1))，9.5n(n-1)lnln(m2n(n-1))}，

(3)

其中A=3.3mnln(mn)，B=10mnlnln(mn).

根据上述定理，在方程(1)中，对任何给定的正整数m和n，利用式(2)，(3)，运用计算机的Maple软件，可迅速求出方程(1)的全部解.

2 引 理

引理1 对于n≥3的正整数n，有

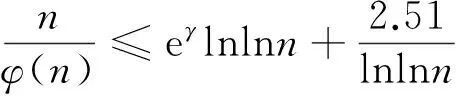
其中，e为自然对数的底，γ为Euler常数.

证明参见文献[18]的定理15.

引理2 对于正整数n≥4，有

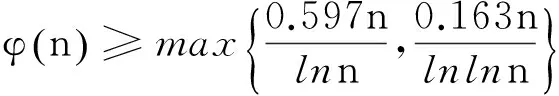
(4)

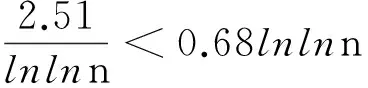
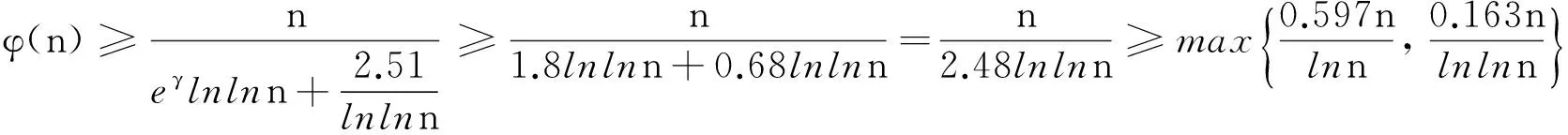
证毕.

3 定理证明

由于对称性，不妨设方程(1)的解(x1，…，xn-1，xn)满足

φ(x1)≤…≤φ(xn-1)≤φ(xn)，

(5)

由于φ(ab)≥φ(a)φ(b)(a，b∈*)，因此由式(5)可得

φ(x1…xn-1)φ(xn)≤φ(x1…xn-1xn)=m(φ(x1)+…+φ(xn-1)+φ(xn))≤mnφ(xn)，

(6)

于是由式(6)可得

φ(x1…xn-1)≤mn.

(7)

若x1…xn-1≤6，由于mn≥6，定理显然成立.现考虑x1…xn-1≥7 的情形.由引理2以及式(7)可得

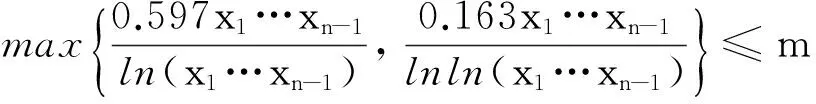
(8)

如果x1…xn-1>A=3.3mnln(mn)，则

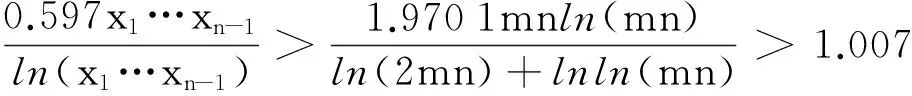
与式(8)矛盾，于是

x1…xn-1≤3.3mnln(mn)=A.

(9)

同理由式(8)可解得

x1…xn-1≤10mnlnln(mn)=B.

(10)

不妨设x1≤x2≤…≤xn-1，则由式(9)～(10)可得

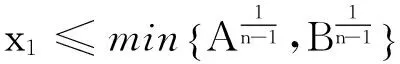
另一方面，设d=gcd(x1，…，xn-1，xn)，根据Euler函数的性质以及式(1)可知

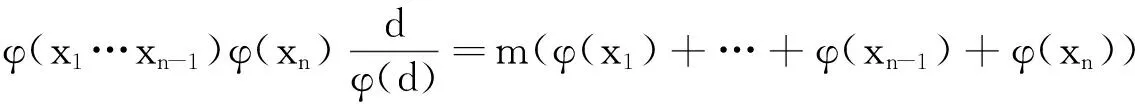
于是

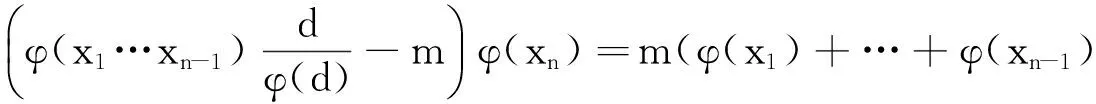
(11)

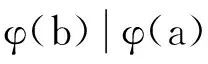
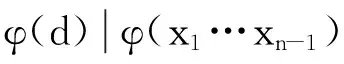
故从式(11)可知

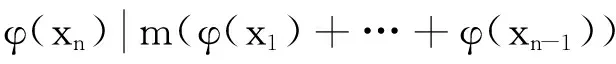
(12)

所以由式(5)和(12)可得

φ(xn)≤m(φ(x1)+…+φ(xn-1))≤m(n-1)φ(xn-1)≤m2n(n-1).

(13)

如果xn≤100，由于m≥2，n≥3，定理显然成立，因此下面考虑xn≥101 的情形.由引理2以及式(13)可得

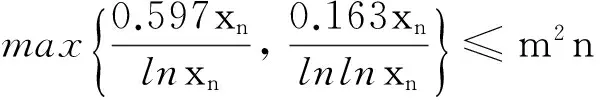
(14)

同理由式(14)可解得

xn≤2.6m2n(n-1)ln(m2n(n-1))，

以及

xn≤9.5m2n(n-1)lnln(m2n(n-1)).

证毕.

4 推论与猜想

在方程(1)中，如果m，n给定，则利用以上的定理可以给出方程的每一个解的较为精确的上界.利用Maple软件，可以迅速地求出方程(1)的全部正整数解.

推论1 方程φ(xyz)=7(φ(x)+φ(y)+φ(z))的所有正整数解(x，y，z)(x≤y≤z)为：(3，4，58)，(3，5，43)，(3，5，49)，(3，5，86)，(3，5，98)，(3，8，43)，(3，8，49)，(3，10，43)，(3，10，49)，(4，4，29)，(4，5，43)，(4，5，49)，(4，6，29)，(5，6，43)，(5，6，49).

证明：在定理1中取m=7，n=3可得，x≤14，y≤210，z≤5 832，在计算机上利用Maple软件搜索，则可得方程仅有以上正整数解.证毕.

推论2 方程φ(xyz)=10(φ(x)+φ(y)+φ(z))的所有正整数解(x，y，z)(x≤y≤z)为：(1，11，121)，(1，11，242)，(1，22，121)，(2，11，121)，(3，4，66)，(3，6，44)，(3，6，50)，(3，7，41)，(3，7，55)，(3，7，82)，(3，7，88)，(3，7，100)，(3，7，110)，(3，8，22)，(3，9，11)，(3，9，22)，(3，10，22)，(3，11，11)，(3，11，13)，(3，11，18)，(3，11，22)，(3，11，26)，(3，11，28)，(3，12，31)，(3，13，22)，(3，14，41)，(3，14，55)，(4，5，22)，(4，6，33)，(4，7，41)，(4，7，55)，(4，7，75)，(4，8，11)，(4，9，41)，(4，9，55)，(4，10，11)，(4，11，11)，(4，11，12)，(4，11，13)，(4，11，21)，(5，5，16)，(5，5，24)，(5，6，22)，(5，8，15)，(6，6，25)，(6，7，41)，(6，7，55)，(6，8，11)，(6，9，11)，(6，10，11)，(6，11，11)，(6，11，13).

证明：在定理1中取m=10，n=3可得，x≤18，y≤336，z≤14 103，在计算机上利用Maple软件搜索，可得方程此时仅有以上正整数解.证毕.

推论3 方程φ(xyzw)=3(φ(x)+φ(y)+φ(z)+φ(w))的所有正整数解(x，y，z，w)(x≤y≤z≤w)为：(1，1，4，26)，(1，1，4，28)，(1，1，4，36)，(1，1，4，42)，(1，1，5，19)，(1，1，5，27)，(1，1，5，38)，(1，1，5，54)，(1，1，6，12)，(1，1，6，26)，(1，1，6，28)，(1，1，7，7)，(1，1，7，14)，(1，1，7，15)，(1，1，7，16)，(1，1，7，20)，(1，1，7，24)，(1，1，7，30)，(1，1，8，19)，(1，1，8，27)，(1，1，9，12)，(1，1，9，16)，(1，1，9，20)，(1，1，10，19)，(1，1，10，27)，(1，1，12，19)，(1，1，14，15)，(1，2，3，12)，(1，2，3，26)，(1，2，3，28)，(1，2，4，13)，(1，2，4，21)，(1，2，5，19)，(1，2，5，27)，(1，2，6，13)，(1，2，7，7)，(1，2，7，15)，(2，2，3，13).

证明：在定理1中取m=3，n=4可得，x≤4，y≤9，z≤98，w≤1 314，在计算机上利用Maple软件搜索，则可得方程仅有以上正整数解.证毕.

推论4 方程φ(xyzwu)=6(φ(x)+φ(y)+φ(z)+φ(w)+φ(u))的所有正整数解(x，y，z，w，u)(x≤y≤z≤w≤u)为：(1，1，1，9，27)，(1，1，1，9，54)，(1，1，1，18，27)，(1，1，2，9，27)，(1，1，3，3，21)，(1，1，3，3，36)，(1，1，3，3，42)，(1，1，3，4，18)，(1，1，3，4，38)，(1，1，3，5，24)，(1，1，3，5，52)，(1，1，3，5，56)，(1，1，3，6，14)，(1，1，3，6，21)，(1，1，3，7，11)，(1，1，3，7，22)，(1，1，3，8，15)，(1，1，3，8，35)，(1，1，3，11，14)，(1，1，4，4，19)，(1，1，4，4，27)，(1，1，4，5，39)，(1，1，4，6，6)，(1，1，4，6，9)，(1，1，4，6，19)，(1，1，4，7，11)，(1，1，4，9，11)，(1，1，5，7，8)，(1，1，5，7，12)，(1，1，5，8，9)，(1，1，6，6，7)，(1，1，6，7，11)，(1，2，2，2，26)，(1，2，2，2，28)，(1，2，2，2，36)，(1，2，2，2，42)，(1，2，3，3，14)，(1，2，3，3，21)，(1，2，3，4，6)，(1，2，3，4，9)，(1，2，3，4，19)，(1，2，3，6，7)，(1，2，3，7，11)，(1，3，3，3，3)，(1，3，3，3，6)，(2，2，2，2，13)，(2，2，2，2，21)，(2，2，3，3，4)，(2，2，3，3，7)，(2，3，3，3，3).

证明：在定理1中取m=6，n=5可得，x≤4，y≤6，z≤18，w≤336，u≤12 316，在计算机上利用Maple软件搜索，则可得方程仅有以上正整数解.证毕.

由以上推论以及已有的计算结论可知，在方程(1)中，其正整数解的最大者很可能不会特别大，因此，进一步研究的问题是：

问题 在方程(1)中，其解的估计式max{x1，…，xn-1，xn}≤Cmn成立吗? 其中C为常数.

致谢：作者衷心感谢阿坝师范学院杨仕椿教授的悉心指导和热情帮助!

[1]GuyRK.Unsolvedproblemsinnumbertheory[M].NewYork：Springer-Verlag，2004：25-56.

[2] 华罗庚.数论导引[M].北京：科学出版社，1979：13-14.

[3]ErdösP.RemarksonnumbertheoryII：someproblemsontheσfunction[J].ActaArith，1959，5：171-177.

[4]MakowskiA，SchinzelMA.Onthefunctionsσ(n)andφ(n)[J].ColoqMath，1964，113：95-99.

[5]FordK.Thenumberofsolutionsofφ(x)=m[J].AnnalsofMath，1999，150：1-29.

[6]SchinzelA.Surequationφ(x +k)=φ(x)[J].ActaArith，1958(4)：181-184.

[7]RobertBaillie.Tableofφ(x)=φ(x+1)[J].MathComput，1976，30(133)：189-190.

[8]MakowshiAndrzej.Onsomeequationsinvolvingφ(n)andσ(n)[J].ArnerMath，1960，67：668-670.

[9]RosenKH.Elementarytheoryanditsapplications[M].AddisonWesley：PearsonEducationInc，2005：225.

[10] 姜友谊.关于Euler函数方程φ(x)=m的解[J].重庆工业管理学院学报，1998，12(5)：91-94.

[11]SunCuifang，ChengZhi.SomekindofequationsinvolvingEulerfunctionφ(n)[J].JMathStudy，2010，43(4)：364-369.

[12] 孙翠芳，程智.关于方程φ(abc)=2(φ(a)+φ(b)+φ(c))[J].数学的实践与认识，2012，42(23)：267-271.

[13] 张四保.不定方程 φ(xyz)=4(φ(x)+φ(y)+φ(z))的解[J].东北石油大学学报，2013，37(6)：113-118.

[14] 张四保.有关Euler函数φ(n)的方程的正整数解[J].数学的实践与认识，2014，44 (20)：302-305.

[15] 孙树东.一个与Euler函数φ(n)有关的方程的正整数解[J].北华大学学报(自然科学版)，2015，16(2)：161-164.

[16] 张四保，刘启宽.关于Euler函数一个方程的正整数解[J].东北师大学报(自然科学版)，2015，47(3)：49-54.

[17] 史保怀，潘晓玮.关于数论函数方程φ(x1…xn-1xn)=m(φ(x1)+…+φ(xn-1)+φ(xn))[J].数学的实践与认识，2014，44(24)：307-310.

[18]RosserJB，SchoenfeldL.Approximateformulasforsomefunctionsofprimenumbers[J].IllinoisJMath，1962，6：64-94.

【责任编辑：伍 林】

Upper Bounds of the Solutions of a Class of Euler’ Functional Equation

Xie Zizhen，Jiang Zhuoling，He Haixia，Huang Meiling

(Department of Mathematics and Finance，A’ba Teachers University，Wenchuan 623000，China)

Letφ(n) is Euler function of a positive integern.The nature of the Euler function is interesting research topics in number theory.On the basis of the literature，we discuss Euler functional equationφ(x1…xn-1xn)=m(φ(x1)+…+φ(xn-1)+φ(xn))，and the more accurate upper bounds of all positive integer solutions of the equation are given.As the application，we obtain all solutions of the equation for some given positive integersmandn.

Euler function；functional equation；positive integer solutions；upper bound of solutions

1009-4822(2016)05-0577-04

10.11713/j.issn.1009-4822.2016.05.004

2016-01-21

四川省教育厅自然科学研究项目(15ZA0337)；阿坝师范学院科研课题项目(JXYZ201506).

谢自珍(1992-)，女，助教，主要从事数论及其应用研究，E-mail：2498188662@qq.com.

O156.1

A