同心导体球壳间非均匀介质中的静电场
2016-10-15董宇欣董超铀
董宇欣,董超铀
(1. 延安大学 物理与电子信息学院,陕西 延安 716000;2. 延安职业技术学院 机电工程系,陕西 延安 716000)
同心导体球壳间非均匀介质中的静电场
董宇欣1,董超铀2
(1. 延安大学 物理与电子信息学院,陕西 延安716000;2. 延安职业技术学院 机电工程系,陕西 延安716000)
根据唯一性定理讨论同心导体球壳之间存在不均匀介质情况的静电场,给出静电场的表达式及电荷的分布.
介电常数;边界条件;唯一性定理
两同心导体球壳之间的静电场,在一些特殊情况,如球壳之间存在均匀电介质(以下电介质均指线性介质),两种不同的均匀的电介质,给出了精确的解[1,2].而对存在非均匀介质情况讨论得较少,本文根据静电场的唯一性定理讨论比文献[1,2]更一般情况的静电场.
1 球壳间存在非均匀介质时的静电场
如果同心导体球壳之间存在非均匀介质,在一般情况,很难求出静电场的精确表达式.但有些特殊情况,如当介质的介电常数可以写成
ε=εr(r)εθφ(θ,φ)

图1
其中εr(r)可以在整个球壳内连续变化,也可以在球壳内按同心球面为边界分块连续变化;εθφ(θ,φ)可以在整个球壳内连续变化,也可以在球壳内按以顶角为球心的立体角(如图1所示:以r方向沿导体球面上任意闭合曲线扫过的曲面所张的立体角)分块连续变化.若把球壳区域分成n个同心子区域Vri;再把球壳区域按以顶角为球心的立体角分成m个同心子区域Vθφj.则Vri与Vθφj的交集区域Vij的介电常数为
εij=εri(r)εθφj(θ,φ)
对于这种电介质分布可以找到满足边界条件和场方程(ρf=0)
n×(E2-E1)=0
(1)
n·(D2-D1)=σ
(2)
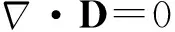
(3)
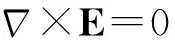
(4)
的解,根据唯一性定理可知此解为静电场唯一解.下面将讨论这种情况.
设导体球壳内充满介电常数为ε=εr(r)εθφ(θ,φ)的非均匀介质,内球壳外径为r0,外球壳内径为rn,分别带电Q和-Q,如果设E为有心场且与r有关,即
E=E(r)er
若介质按上述分块均匀,则各分区域侧面两侧的电场与边界面相切并有相同的数值,各分区域底面电场的切向分量为零,因此边界条件式(2)得到满足且由于Er=E(r),Eθ=Eφ=0,所以在介质中满足

则各分区域侧面D的法向为零,各分区域底分界面两侧的D连续,因此边界条件式(1)也得到满足.球对称的E在导体球面上处处与球面垂直,因而保证导体球面为等势面.待定常数A与总电荷Q满足(下式中S为球壳第i层同心子区域内任意同心球面,Sj为S在第j个立体角子区域的部分,所张立体角为Ωj)
所以
故
(5)
(6)
2 导体及电介质的电荷分布
由于D不具有球对称性,因此导体球面的自由电荷分布应与电介质的分布有关;而E具有球对称性,所以总电荷(自由电荷与极化电荷之和)的分布也具有球对称性,只是在径向的分布与电介质有关.下面讨论自由电荷、极化电荷和总电荷的分布.
2.1自由电荷分布
自由电荷仅在导体球面,所以内导体外球面、外导体内球面的自由电荷分布分别为:
(7)
(8)
由式(7)和式(8)可知导体球面上的自由电荷不是均匀分布,仅与电介质的介电常数中的εθφ(θ,φ)有关,随θ、φ的变化而变化.
2.2极化电荷分布
球壳内的极化电荷可分为电介质内的体电荷、电介质与电介质分界面的面电荷及电介质与导体分界面的面电荷,其体电荷和面电荷密度分别为:
体极化电荷
(9)
电介质与电介质分界面极化电荷面密度为
(10)
电介质与导体分界面极化电荷面密度(r=r0,rn分别为导体表面与同心子区域分界面,在导体内有P=0)为:
(11)
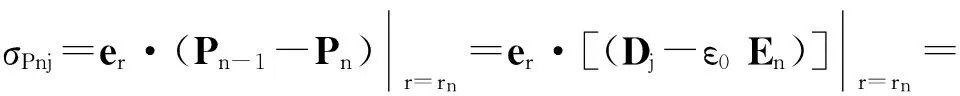
(12)
从式(9)可以看出各层电介质中的体极化电荷球对称分布,与各立体角子区域无关;从式(10)也可以看出各层电介质分界面的面极化电荷均匀分布,也与各立体角子区域无关;从式(11)和式(12)可以看出导体表面与同心子区域分界面上的面极化电荷不是均匀分布,但两分界面上自由电荷与极化电荷之和:
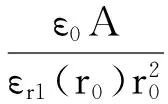
则为均匀分布,从而保证电场的球对称性.
3 球壳间存在分块均匀介质时的静电场
设同心导体球壳内球外径为r0,外球内径为rn,分别带电Q和-Q,导体球壳内按块均匀分布着介电常数不同的电介质,其中第i层,第j立体角子区域电介质的介电常数为εij,如果第i层子区域的电介质满足
ki为仅与i有关的常数,则
εij=kiε1j=εri(r)εθφj(θ,φ),(j=1,2,…,m)
即
εri(r)=ki,εθφj(θ,φ)=ε1j
所以A的分母积分为
把上式分别代入式(7)—式(12)可得到球壳内的电场、电荷表达式,这里只写出电场和电位移的表达式如下:
即在同一层同心球壳子区域中电场强度的表达式相同;在同一立体角子区域电位移的表达式相同.下面通过具体例子来讨论球壳间存在分块均匀介质时的静电场.设同心球壳各子区域中电介质的介电常数为
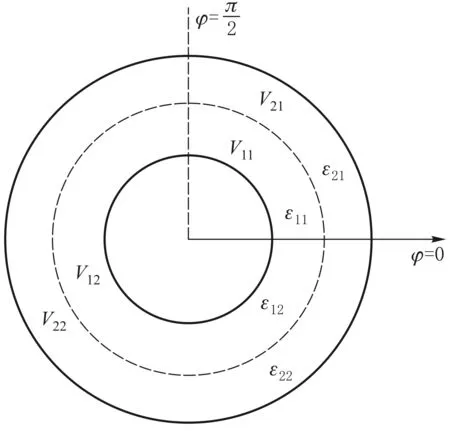
图2
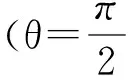
ε11=k1ε11=1ε0,ε21=k2ε11=3ε0,
ε12=k1ε12=1·2ε0,ε22=k2ε12=3·2ε0
则εr1=k1=1,εr2=k2=3;εθφ1=ε0,εθφ2=2ε0,所以A的分母积分为
故根据式(7)—式(12)可得到球壳内的电场表达式为:
极化体电荷密度为
导体球壳的面电荷密度为:
电介质与导体球壳分界面的极化电荷面密度为:
两介质分界面的极化电荷面密度为
电介质与导体球壳分界面的总电荷面密度为:
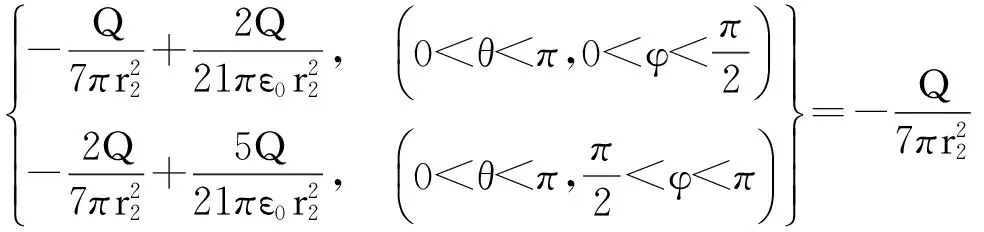
通过以上计算可知,σr0f和σr2f、σP0和σP2不是均匀分布,它们之和σr0、σr2仍然保持均匀分布,如前述分析从而保证E的球对称分布.
3 球壳间存在分块均匀介质时的电容
导体球壳间存在分块均匀介质时两球壳的电压为
所以导体球壳间存在分块均匀介质时体系电容的倒数满足
其中
Cij可看作子区域Vij的电容,Ci则为第i层同心球壳子区域Vi的电容.因此第i层同心球壳子区域Vi的电容为第i层各子区域Vij电容的并联,导体球壳体系的电容为各层同心球壳子区域Vi电容的串联.还可以证明第j同心立体角子区域Vj的电容为第j同心立体角各子区域Vij电容的串联,导体球壳体系的电容为各同心立体角子区域Vj电容的并联.
[1]赵凯华,陈熙谋.电磁学(上册)[M].北京:高等教育出版社,1978:161.
[2]郭硕鸿.电动力学 [M].北京:高等教育出版社,1979:64.
Electrostaticfieldbetweentwoconcentricconductivesphericalshells
DONGYu-xin1,DONGChao-you2
(1.SchoolofPhysicsandElectronicInformation,YananUniversity,Yan’an,Shaanxi716000,China;2.Yan’anInstituteofVocationandTechnology,Yan’an,Shaanxi716000,China)
Electrostaticfieldisdiscussedwhentherearenon-uniformdielectricsbetweentwoconcentricconductivesphericalshellsusinguniquenesstheorem.Expressionsofelectrostaticfieldanddistributionofelectricityaregiven.
dielectricconstant;boundarycondition;uniquenesstheorem
2015-02-27;
2015-08-09
董宇欣(1988—),女,陕西延安人,延安大学物理与电子信息学院教师,硕士,主要从事电磁理论的教学工作.
O441
A
1000- 0712(2016)01- 0020- 04
