周期驱动下保守椭圆摆系统的混沌运动
2016-10-15陈建宏吴学勇董向成
陈建宏,吴学勇,刘 昊,董向成
(兰州城市学院 培黎工程技术学院, 甘肃 兰州 730070)
周期驱动下保守椭圆摆系统的混沌运动
陈建宏,吴学勇,刘昊,董向成
(兰州城市学院 培黎工程技术学院, 甘肃 兰州730070)
运用广义拉格朗日方程,对周期驱动下的椭圆摆运动过程建立了模型方程.利用数值方法求解该方程,研究了该系统在周期驱动作用下不变环面的变形、破裂以及产生混沌运动的过程.并且,利用最大李雅普诺夫指数研究了驱动频率及质量参数对其混沌运动的影响.
周期驱动;椭圆摆;混沌运动
在大学物理教学中,往往会遇到如图1所示的一种简单模型.一个质量为m1、半径为R的半球形光滑凹槽放置在光滑水平面上,再将一质量为m2的质点置于凹槽内角位置θ处,质点由静止状态自由下滑. 可以证明,质点相对地面静止参考系的运动轨迹是椭圆线,故该系统是一种典型的椭圆摆系统[1,2].在大学物理相关内容中,该体系被假定为一个不受外力作用的理想系统.在本文中,我们将考虑来自外界的周期驱动对该系统运动行为的影响.众所周知,保守单摆系统在外力驱动下具有非常丰富的非线性运动行为[3,4].不难想象,当存在周期驱动F(t)时,不仅椭圆摆系统动力学更有实际意义,其行为也将更加丰富.
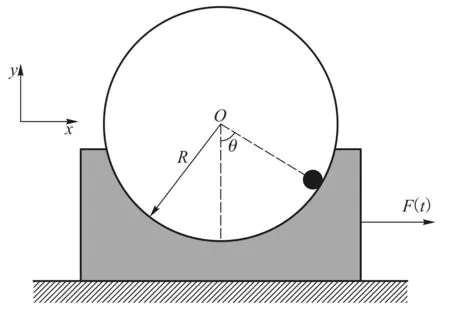
图1 基本模型
1 模型方程的建立
为了研究方便,我们将质点的运动约束在半径为R并且固连在凹槽上的圆环内.在图1中,以凹槽在运动初始时刻球心所在的O点为坐标原点.在地面参考系中建立坐标系.Ox轴沿水平方向,Oy轴沿竖直方向.在地面参考系中,令凹槽最低点在运动过程中的坐标为(x,-R),则质点在运动过程中的坐标为(x+Rsinθ,-Rcosθ).容易得到,椭圆摆体系的拉格朗日函数为[5]
(1)
式(1)中m1为凹槽的质量,m2为质点的质量.现向凹槽上施加一个沿着Ox轴方向的周期驱动力F(t)=F0cos(ωDt+π),再将式(1)及该驱动力代入广义拉格朗日方程[6],从而得到椭圆摆在周期外力驱动下的动力学方程
(2)
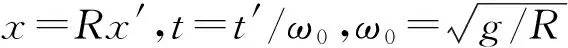
代入(2)式,略去撇号,经过化简得到无量纲方程
(3)
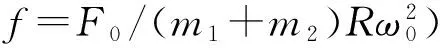
2 数值结果及分析
2.1不变环面的变形、破裂以及混沌运动
为了有效控制数值误差,本文采用四阶隐式格式的龙格-库塔方法数值求解方程(4),其中计算步长为0.01.首先,将无量纲的驱动频率固定为Ω=4,质点和凹槽的质量固定为m1=5和m2=1 (或μ≈0.19).图2和图3给出了以驱动周期为采样间隔,系统在不同驱动强度f下的庞加莱截面.方程(4)的初始条件为:θ(0)=5°、 35°、 65°、95°、125°,θ′(0)=0,x(0)=0,x′(0)=0.为便于区分,我们将不同初始条件对应的轨道在图2中分别标记为1—5.图2(a)和图2(b)是没有外界驱动时的情况.其中,图2(a)和无驱动时单摆[3,4]的运动规律类似,即在确定的能量下系统具有确定的相轨道,并且不同初始能量的相轨道彼此不相交.而图2(b)则反映出与图2(a)不同的特点:1)轨道1—5都相交于坐标原点;2)轨道5(对应θ(0)=125°)在x′(t)=0附近还存在两个对称的小圈.这表明:当质点具有较大初始角度时,凹槽的运动并不是单周期的.根据非线性动力学理论[7],我们将轨道1—5称为不变环面.图2(c)和图2(d)对应驱动强度f=0.2.从图2(c)可以看出,轨道1—5均发生了变形,变得左右不对称了,其中轨道5被扭曲得最为明显.在图2(d)中,除了轨道5中两个小圈变得不对称外,其他轨道均没有明显的变形.图3(a)和图3(b)对应驱动强度f=0.22.可看出,当驱动进一步增强时,轨道5出现了破裂.图3(c)和图3(d)对应驱动强度f=0.44.此时,轨道5已经完全破碎了,说明轨道5的运动进入了混沌运动.图3(c)类似于单摆系统的情形:即使轨道5发生破裂,但是破裂后的轨迹无法进入轨道1—4的所处的区域.但在图3(d)中:当轨道5破裂后,其破裂的轨迹完全进入了轨道1—4所处的区域.需要注意的是,这点与单摆是完全不同的.事实上,当驱动强度进一步增强时,图3(c)和图3(d)反映的规律依然存在.
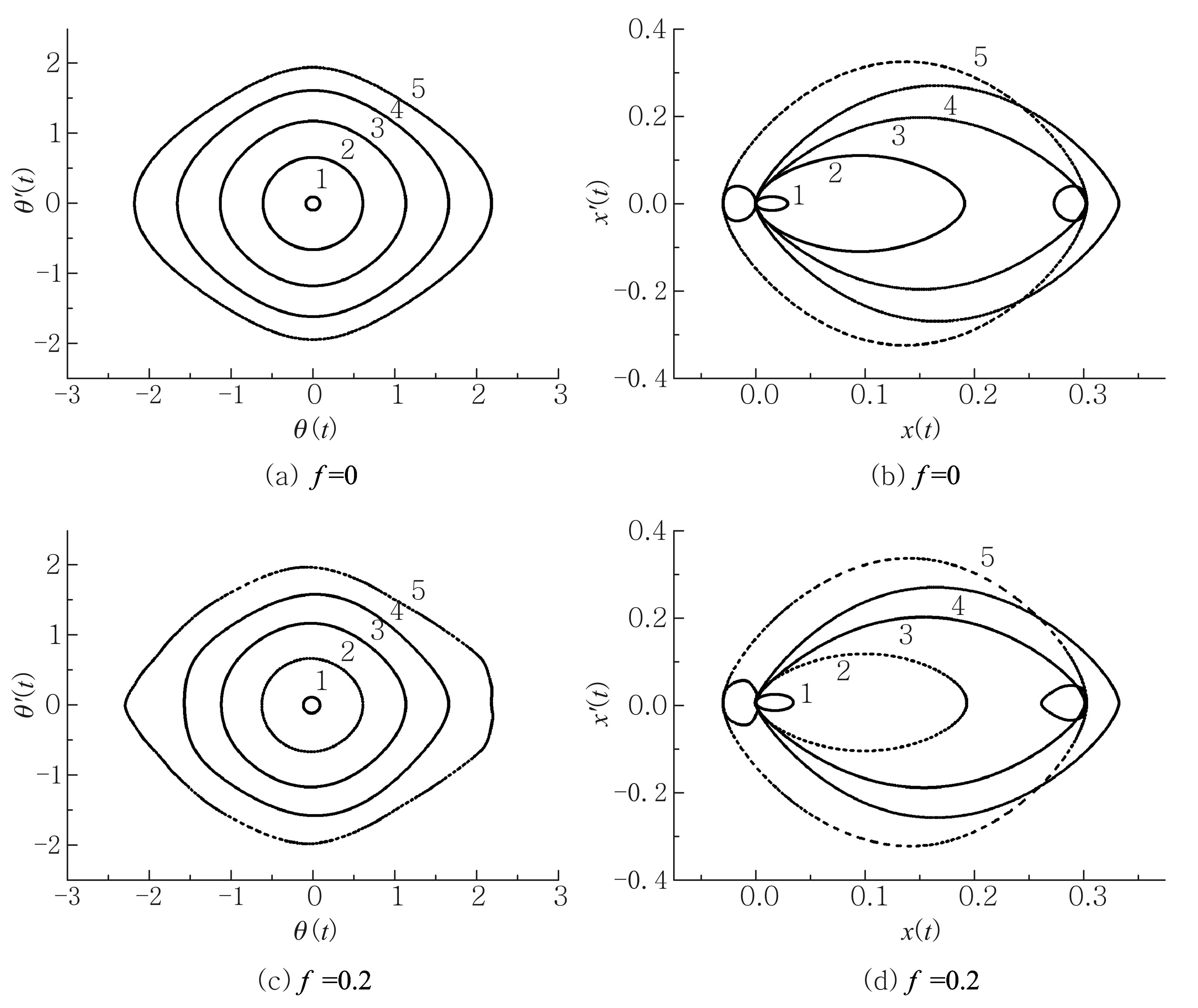
图2 不变环面及其在驱动下的变形
为了从整体上把握混沌现象出现与驱动强度的关系,本文绘出系统最大李雅普诺夫指数随驱动强度变化的图像.对于给定的驱动强度,采用以下公式计算最大李雅普诺夫指数λ[7]:
(4)
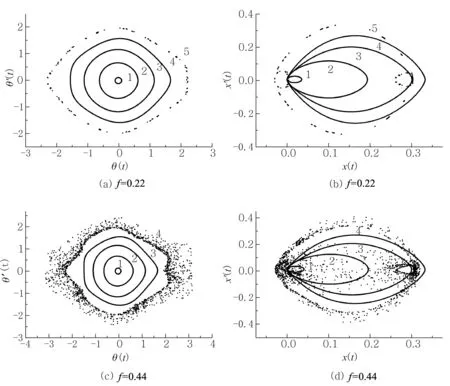
图3 不变环面的破裂和破碎
式(4)中d0为初始扰动值,d(t)为在t时刻相空间内轨道的分离值.在实际计算中,为了方便计算d(t),时间分割成了k个时段,τ为时间间隔,则有t=kτ.在本文计算中,时间长度t=4 000,则时间间隔τ=2,将最后200个数据取平均得到最大李雅普诺夫指数.图4是轨道5对应的最大李雅普诺指数λ与驱动强度f的关系.从图4可以看到,当驱动强度f<0.43时,最大李雅普诺夫指数λ≈0,此时系统的运动是准周期振荡;而当驱动强度f=0.43时,最大李雅普诺夫指数发生跃变.也就是说,当f>0.43时轨道5对应的运动突然进入了混沌状态.这与图3中庞加莱截面所反映规律的是一致的.
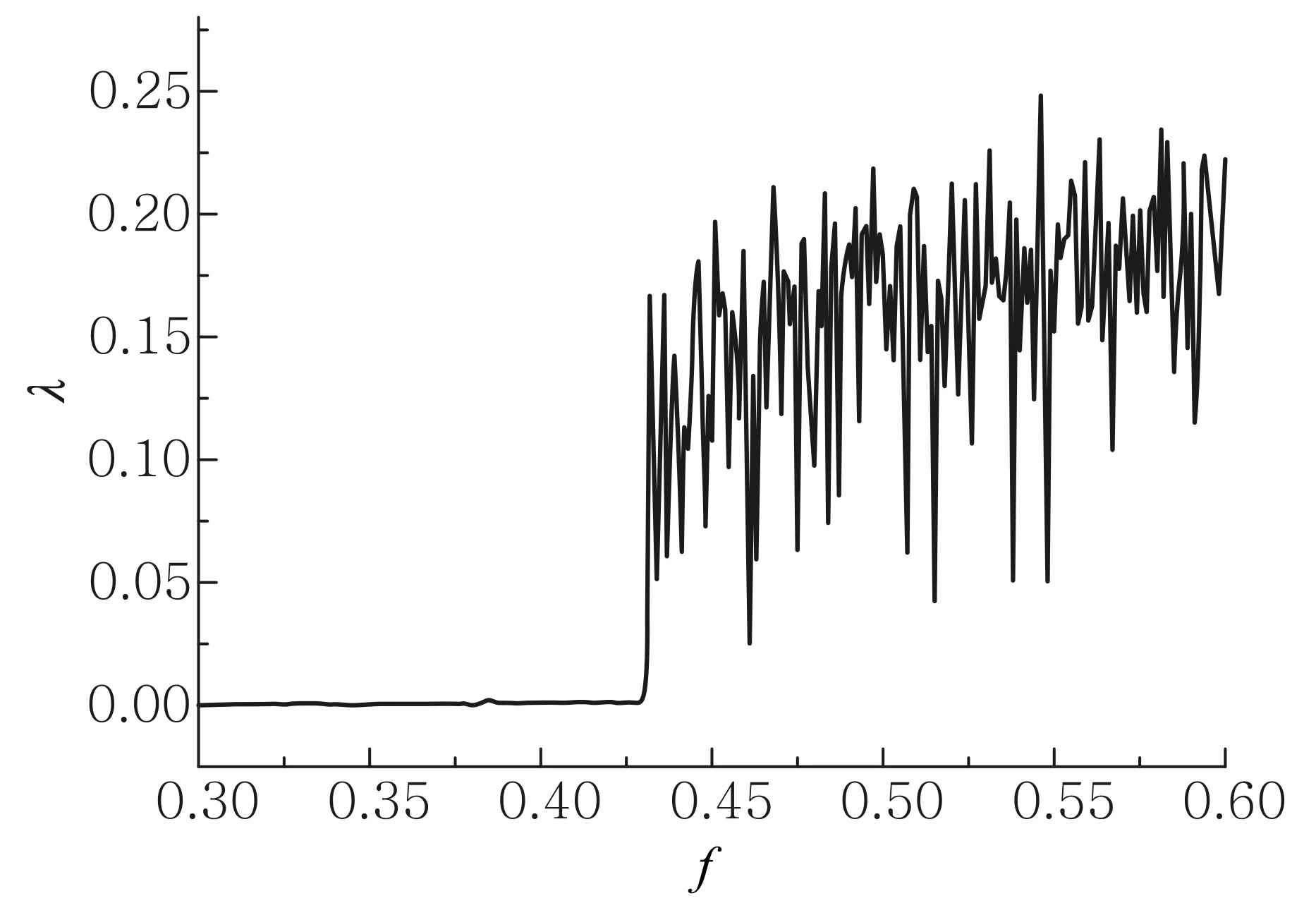
图4 μ=0.19,Ω=4,轨道5对应的λ-f关系
2.2驱动频率及质量参数对混沌运动的影响
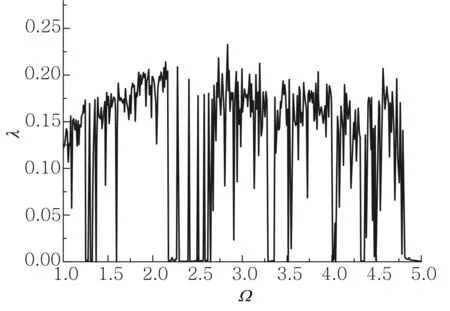
图5 μ=0.19,f=0.44,轨道5对应的λ-Ω关系
图5是当μ=0.19,f=0.44时系统的最大李雅普诺夫指数λ随驱动频率的变化关系.可以看出,在大部分情况下,系统的最大李雅普诺夫指数处于0.15左右,说明系统处于混沌运动状态;但少数情况下,最大李雅普诺夫指数会突然降到零左右,说明系统此时处于准周期状态.并且,最大李雅普诺夫指数为零时,驱动频率还有一定的宽度.如Ω=2.295~2.383这个频率区间,最大李雅普诺夫指数持续为零.最大李雅普诺夫指数持续为零的频率宽度也不一样,如在Ω=4.01时,李雅普诺夫指数会突然为零,然而当驱动频率稍有所增大(Ω=4.05)或者减小(Ω=4),李雅普诺夫指数会跃变到0.15左右,即轨道5又进入混沌运动.
我们还研究了系统的质量参数μ对系统混沌运动的影响.图6是Ω=4,f=0.44时,轨道5对应的最大李雅普诺夫指数λ与质量参数μ的关系.可以看出,当质量参数μ>0.18时,最大李雅普诺夫指数在0.15左右,系统将处于混沌状态.当质量参数μ<0.18,还存在一些李雅普诺夫指数持续为零区间.这说明当μ<0.18,系统质量参数对系统混沌运动具有明显的影响.此时,系统质量参数的改变将可能使系统从准周期状态进入混沌状态,或者从混沌状态进入准周期状态.
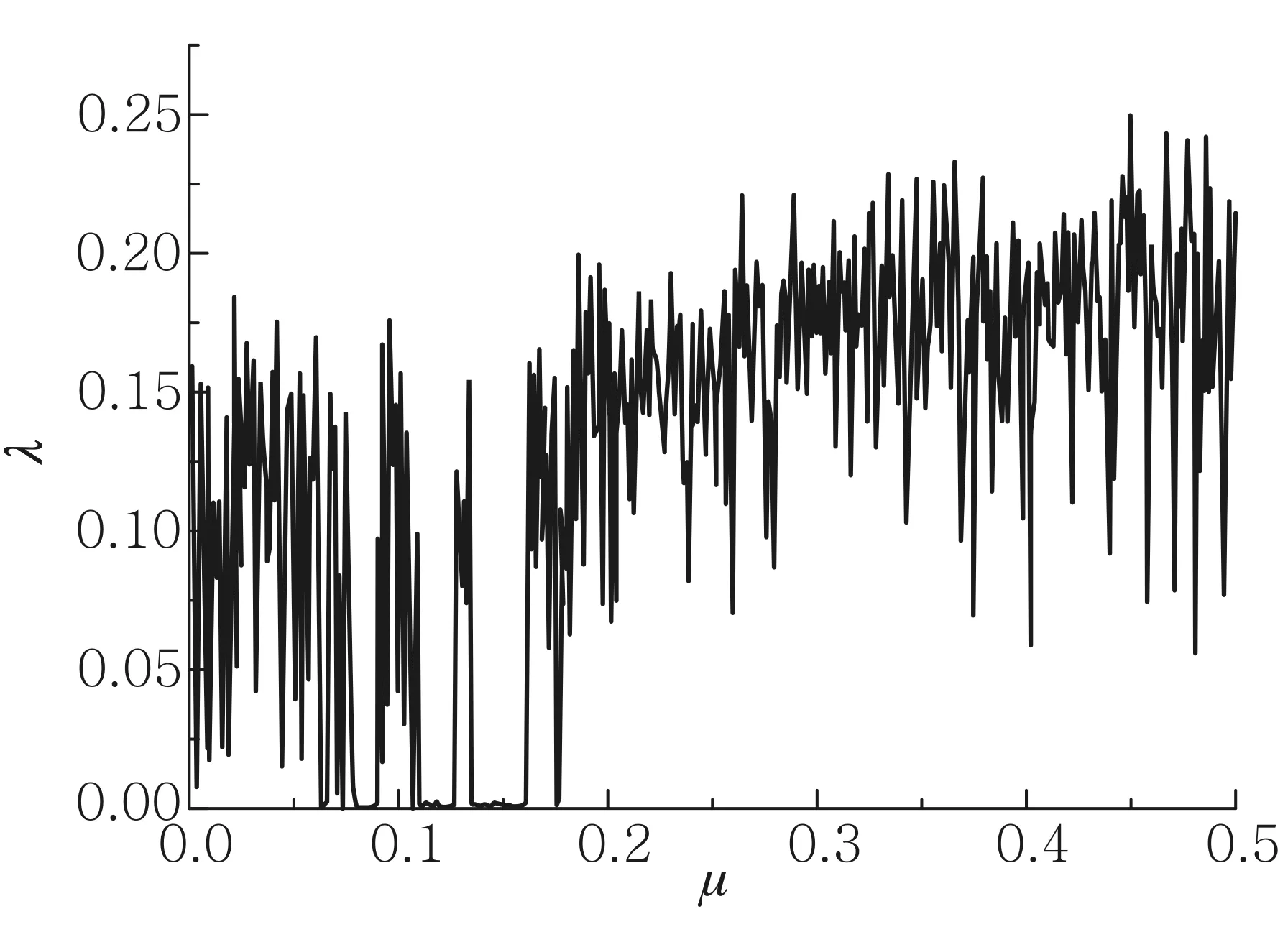
图6 Ω=4,f=0.44,轨道5对应的λ-μ关系
最后需要指出,图4~图6中的最大李雅普诺夫指数随参数波动都比较大.这主要因为其对参数依赖比较大.对此我们举例给出解释.当取f=0.4,μ=0.19,Ω=4,d0=0.001时,最大李雅普诺夫指数随k的变化关系图像如图7(a)所示,可以看出:最大李雅普诺夫指数随着k增大趋于一个定值.将最后200个数据取平均得到λ≈0.000 09.图7(b)则是上述参数下x-x′平面的相图.图7(a)和图7(b)的结果均表明: 此时系统处于准周期运动状态.如果其他参数不变,令f=0.5,最大李雅普诺夫指数随k的变化关系图像如图7(c)所示,可以看出:最大李雅普诺夫指数随着k增大并没有趋于一个定值.将最后200个数据取平均得到最大李雅普诺夫指数λ≈0.182 945.此时x-x′相图如图7(d)所示.图7(c)和图7(d)的结果均表明:此时系统处于混沌运动状态.根据以上两种不同情况,我们认为:通过最大李雅普诺夫指数的值,可以判断系统是处于准周期状态还是混沌运动状态,并且可以通过相图的结果得到验证.以上两例也同时表明,系统运动行为对参数依赖比较大.然而,在一些情况下如图7(c),最大李雅普诺夫指数不趋于一个定值,我们采用最后200个数据的平均的结果,这种处理办法肯定存在计算误差.
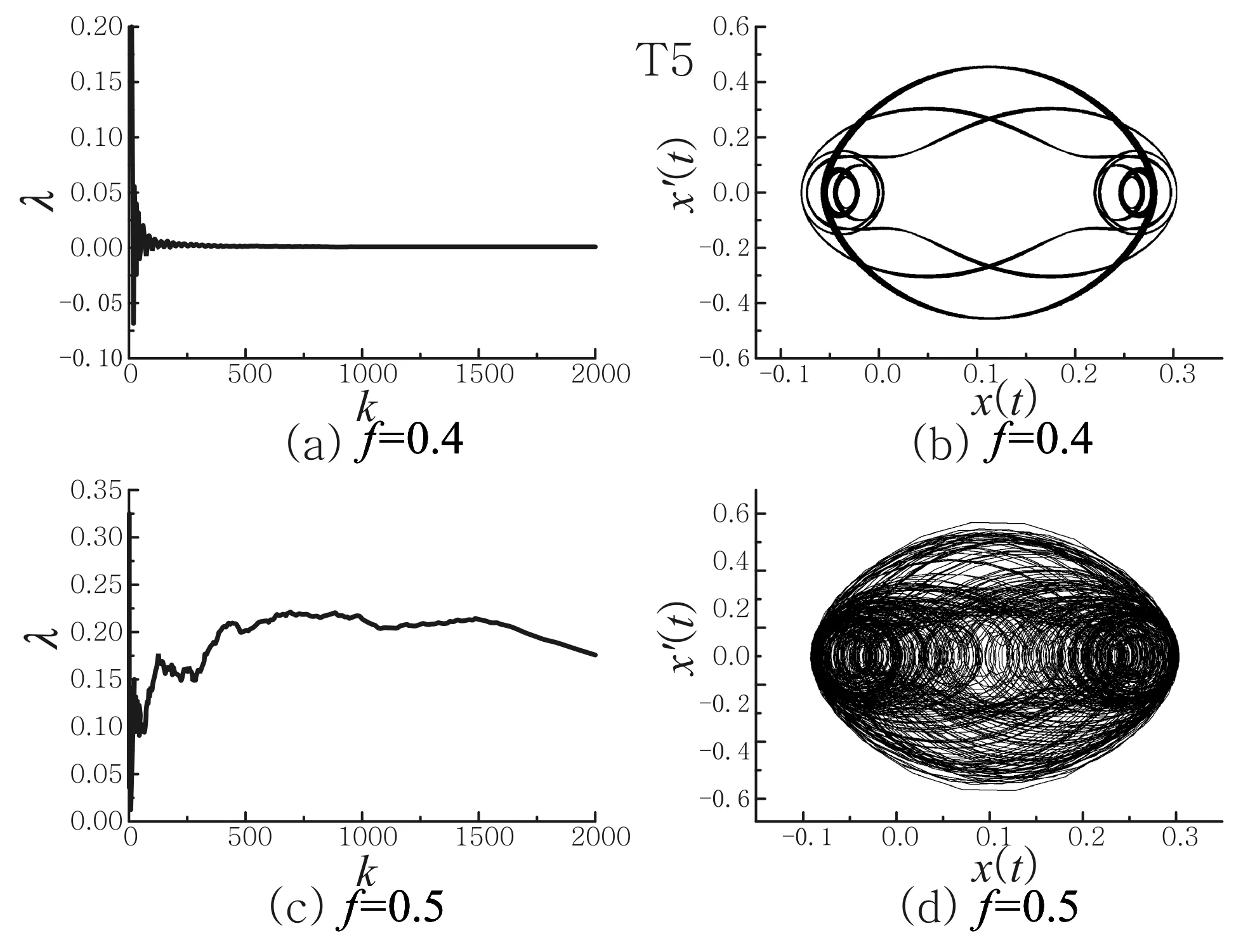
图7 λ-k关系图像及系统在平面相图.其中μ=0.19,Ω=4,d0=0.001
3 结论
本文的研究表明:椭圆摆系统在周期驱动下,具有极其复杂的非线性运动行为.这包括:1)当某一不变环面破碎时,摆角θ对应的相轨迹与其他未破碎的不变环面是不相交的,而凹槽位置x对应的相轨迹与其他不变环面则是相交的;2)驱动频率对系统的混沌运动具有明显的影响;3)在一定的取值范围内,质量参数对系统的混沌运动具有明显影响.需要强调,本文所考虑系统为保守系统,其运动行为中的混沌现象与外力的加入直接相关,即无驱动下没有混沌.然而,对于像洛伦兹系统、罗斯勒系统那样的耗散体系,即使在无驱动下系统依然有可能产生混沌运动[7].
[1]陈钢, 阮中中. 椭圆摆的一种实现方法[J].大学物理, 2006, 25(5): 18-20.
[2]李慧娟. 质点沿可自由移动的光滑凹槽的运动分析[J].大学物理,2007,26(7):18-19.
[3]李元杰.单摆的规则随机及混沌运动的研究[J].大学物理, 1998, 17(9): 6-8.
[4]符五久, 饶黄云. 单摆系统通向混沌的道路[J].大学物理,2008, 27(1): 5-10.
[5]陈建宏,魏秀芳,王志全. 可自由平动光滑凹槽中质点运动的数值分析[J].大学物理, 2015, 34(5): 11-14.
[6]郭应征,周志红. 理论力学[M]. 北京:清华大学出版社,2005.
[7]刘秉正, 彭建华. 非线性动力学[M]. 北京: 高等教育出版社,2004.
The chaotic behavior in a conservative elliptical pendulum system under periodic perturbation
CHEN Jian-hong, WU Xue-yong, LIU Hao, DONG Xiang-cheng
(School of Bailie Engineering and Technology, Lanzhou City University, Lanzhou, Gansu 730070, China)
The motion equations of an elliptical pendulum system under periodic perturbation are derived by using the generalized Lagrange equation. The equations are solved numerically to investigate the process of the deformation, distortion, split of the invariant torus and the chaos. Moreover, the influences of the perturbation frequency and the mass parameter on the chaotic behavior are discussed through analyzing the maximum Lyapunov exponent.
periodic perturbation; elliptical pendulum; chaotic behavior
2015-06-09;
2015-11-20基金项目:国家自然科学基金(11164012);兰州市科技计划项目(2012-2-105);兰州城市学院本科教育教学研究项目(2014-jy-01)资助.作者简介: 陈建宏(1982—),男,甘肃平凉人,博士,兰州城市学院培黎工程技术学院副教授,主要从事理论物理研究及计算物理教学工作.
O 415.5
A
1000- 0712(2016)04- 0007- 04
