光频率变换公式的跃迁辐射解释以及光子概念的实质
2016-10-15罗凌霄
罗 凌 霄
(大理大学 工程学院,云南 大理 671003)
光频率变换公式的跃迁辐射解释以及光子概念的实质
罗 凌 霄
(大理大学 工程学院,云南 大理671003)
把质能关系、质速关系、光子假说和跃迁辐射假说结合起来,导出了光频率变换公式,并且写出速度不很快的情况下自由粒子跃迁辐射的频率公式.最后对光子概念的实质作了简单介绍.
光的频率变换公式;跃迁辐射;光子概念;实质
狭义相对论按光的波动理论和洛伦兹变换,对光的频率变换公式作了唯象的解释[1,2].这里我们要给出光的频率变换公式的跃迁辐射解释.在推导中,我们将用到能量守恒定律、动量守恒定律、质能关系式、质速关系式、光子假说、跃迁辐射假说和相对论速度变换关系.
1 运动的自由粒子的跃迁辐射
如图1所示,在惯性系S中,有一个速度为v2的不受力的粒子(即自由粒子)沿x轴正向运动,其动质量为m2,能量为E2,静止能量为E02.这个粒子向低能态跃迁,向着与x轴方向(也就是粒子的初速度方向)成θ角的方向发出一粒频率为ν的光子.跃迁后粒子速度为v1,运动方向与x轴的夹角为β,动质量为m1,能量为E1,静止能量为E01.为方便起见,我们用E02和E01分别表示粒子跃迁前、后所处的能态.这里所说的粒子包括原子、分子、离子等等.
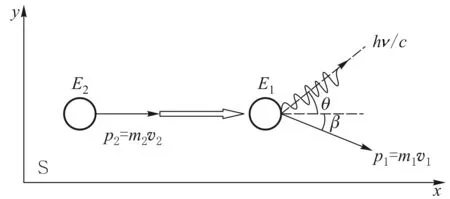
图1
根据能量守恒定律、动量守恒定律、光子假说和跃迁辐射假说,则有
E2=E1+hν
(1)
(2)
(3)
根据质能关系和质速关系,上述3个方程可以写成
(4)
(5)
(6)
由式(5)和式(6)分别得
(7)
(8)
式(7)加式(8),得
(9)
由式(4)得
(10)
式(10)减式(9),得
(11)
解式(11),得
(12)
为方便起见,把速度v2换成v,于是式(12)写成
(13)
这就是以速度v运动的自由粒子从高能态E02向低能态E01跃迁,发射出一粒光子,光子运动方向与初速度v成θ角时光的频率公式.
2 初速为零的自由粒子的跃迁辐射
如图2所示,设有另外一个参考系S′的坐标轴x′、y′分别与S系的x、y平行,并且S′系以速度v沿x轴运动,或者反过来说S系相对于S′系以(-v)的速度沿x轴负方向运动.那么对S′系来说,上一节所说的自由粒子在发生跃迁之前是静止的. 对S′系来说,自由粒子从高能态E02向低能态E01跃迁时,发射的光子的频率为ν′,光子运动方向与x′轴的夹角为θ′.
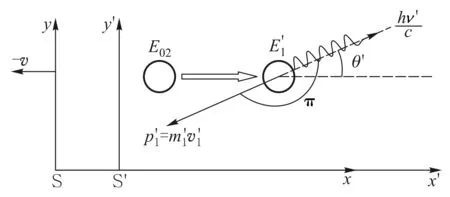
图2
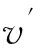
(14)
(15)
根据质能关系和质速关系,上述两个方程可以写成
(16)
(17)
式(17)两边平方,经过一系列过程,得
(18)
把它代入式(16),解得
(19)
这就是原先静止的粒子从高能态E02跃迁到低能态E01时发射的光子的频率公式,显然频率与角度θ′无关.
式(19)也可以从式(13)推出:令v→0,就可以得出式(19).由于式(13)中θ是发射的光子的运动方向与粒子初速度之间的夹角,所以我们不说令v=0就得出式(19).
3 光的频率变换公式
于是,式(13)可以表示为
(20)
为了使上式右端出现的角度是S′系中光子速度与x′轴的夹角θ′,我们要根据相对论速度变换公式, 来推导θ与θ′的关系.
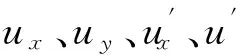
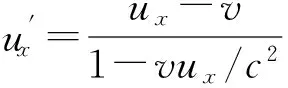
(21)
(22)
把ux=ccosθ和uy=csinθ代入其中,得
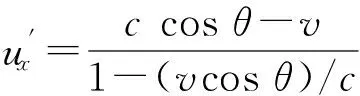
(23)
(24)
于是
(25)
(26)
根据式(25)可以推出
(27)
把它代入式(20),得
(28)
虽然我们是在假定自由粒子跃迁之前相对于S系以速度v运动,而相对于S′静止的情况下推出了式(28),但是它所表达的频率变换规律是普遍成立的.理由如下:对于上述的惯性系S和相对于它以恒定速度v运动的S′系,S′系中频率一定、传播方向一定的光相对于S系的频率应该是一定的,也就是说频率变换公式中的参量与光源的发光机理以及光源的运动情况无关.所以我们通过自由粒子跃迁发光和假定自由粒子在S′系中初速为零推得的频率变换公式就是一般情形的光的频率变换公式.
由于S系相对于S′的速度为(-v),根据物理规律的协变性,从式(28)直接得到
(29)
式(29)也可以从式(20)直接推出.式(29)还可以表示为
(30)
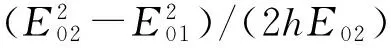
(31)
(32)
式(31)和(32)叫作光的多普勒公式,其中的ν0叫作静止的光源发出的光的频率.但是说光源静止并不确切,因为如上所述,一个原先静止的粒子发光后也要发生反冲运动.所以式(20)、(28) 、(29)和式(30)的表述更为清楚.特别是式(28)和式(29)两式更为优雅,它们将与两个参考系有关的量分别放在了等号两边.
需要说明的是,要根据θ确定θ′,那么式(26)也是需要的,并不多余.
4 自由粒子跃迁辐射的近似频率公式
对于原子、分子、离子之类的粒子,跃迁后粒子的相对论能量几乎不变,于是根据式(13)得
(33)
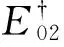
(34)
再考虑到通常粒子的速度远远小于真空光速,可以略去二次项v2/c2,于是
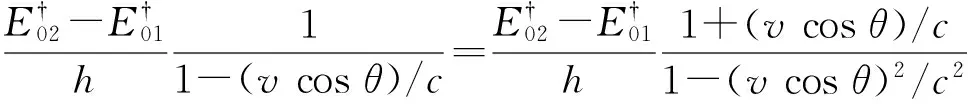
(35)
或者更粗糙地写成
(36)
这就是玻尔的跃迁辐射公式.玻尔本人把它叫做频率条件[3].玻尔似乎不情愿用光量子概念来解释他的频率条件,也许他对光量子概念疑虑很深.
5 光子概念的实质
上面我们利用了光子概念,但光子实际上不是粒子,而是场量子,运用光子概念只是为了方便.量子场论认为[4,5]:频率为ν、波矢量为k的平面简谐电磁波列的能量ε=(n+1/2)hν,动量p=(n+1/2)ћk,量子数n=0,1,2,….所以,当频率和波矢量固定时,电磁场能量的变化量只能是hν的整数倍,电磁场动量的变化量只能是ћk的整数倍.电磁场就是由大量的这样的平面简谐波列组成.当电磁场和粒子相互作用,导致n增加1时,我们习惯于说粒子沿k方向辐射了一粒频率为ν的光子;导致n减少1时,我们习惯于说粒子吸收了一粒沿k方向运动的频率为ν的光子.
一定的封闭空间区域内电磁场的能量就是各式各样被容许的平面简谐电磁波列能量的总和.当所有波列的量子数n全部取零的时候,总能量叫做零点能,为无穷大.其他情况下的总能量也是无穷大.通常所说的电磁能就是实际的能量减去零点能.零点能也就是通常所说的电场强度和磁场强度都为零的真空的能量.
一定的封闭空间区域内电磁场的动量就是各式各样被容许的平面简谐电磁波列的动量的矢量和,它可以等于零.
电磁场具有零点能已经被卡斯米尔效应证明[6,7].真空中两个不带电的平行金属板之间除了万有引力之外还存在别的吸引力,这是因为真空中充满量子数n=0的各种频率的平面简谐电磁波列,但是金属板之间垂直于板面的方向上传播的波形成驻波,只能容纳由板间距决定的频率取一特定系列分立值的波,和两金属板外侧的波相比频率有缺损,所以金属板外侧面受到零点电磁波的压力大于内侧面受到零点电磁波的压力,所以表现为两个金属板相互吸引.
[1]R.瑞斯尼科.相对论和早期量子论中的基本概念[M].上海:上海科学技术出版社,1978:77-83.
[2]中野董夫.相对论[M].北京:北京师范大学出版社,1989:82-87.
[3]曾谨言.量子力学(卷Ⅰ)[M].3版.北京:科学出版社,2000:14-19.
[4]曾谨言.量子力学(卷Ⅱ)[M].3版.北京:科学出版社,2000:643-647.
[5]曹昌祺.辐射和光场的量子统计理论[M].北京:科学出版社,2006:14-24.
[6]苏汝铿.量子力学[M].2版.北京:高等教育出版社,2002:288-291.
[7]倪光炯,陈苏卿.高等量子力学[M].2版.上海:复旦大学出版社,2004:193-197.
The transition radiation explanation about the frequency conversion formula of light and the essence of photon concept
LUO Ling-xiao
(Faculty Engineering, Dali University, Dali, Yunnan 671003, China)
Combining the mass energy relation, mass velocity relation, photon hypothesis and transition radiation hypothesis, the frequency conversion formula of light is deduced. The transition radiation frequency formula of a free particle is obtained in the case of the speed being not fast. Finally, a simple introduction about the essence of photon concept is given.
frequency conversion formula of light; transition radiation; photon concept;essence
2015-07-17;
2015-11-17
罗凌霄(1964—),男,白族,云南剑川人,大理大学工程学院教授,主要从事电磁场理论教学和研究工作.
O 462
A
1000- 0712(2016)04- 0011- 04
