城市电网负荷特性分析方法研究

孙　晓，曾浩宇，梁　维，杨丹青

（1. 湖南工业大学 机械工程学院，湖南 株洲 412007； 2. 湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

城市电网负荷特性分析方法研究

孙晓1，曾浩宇2，梁维2，杨丹青2

（1. 湖南工业大学 机械工程学院，湖南 株洲 412007； 2. 湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

针对累积式自回归-移动平均模型在现代城市降温负荷预测中准确性不高的问题，提出一种双因子累积式自回归-移动平均模型，并用两种模型进行预测。经对比后发现，新模型通过引入平均温度算子，有效提高了城市降温负荷预测的准确性，并对现代城市有较好的普适性。

电网；负荷分析；负荷预测；ARIMA模型

0　引言

城市电网负荷特性，是电力公司对城市电网发展趋势研究以及电网建设方案制定的重要参考依据［1］。近年来，工业发展模式从粗放型转变成资源节约型，高能耗工业增长缓慢甚至萎缩，城市居民生活用电比例明显增加，景观用电量持续增长，现代城市电网的负荷特性变得更加复杂。如何进行新形势下的城市电网负荷特性分析成为了行业难题。

在“十二五”期间，某市地区经济呈现较大持续增长势头，产业结构优化明显，居民的生活水平和生活质量显著提高，居民用电量持续增加。随着空调的普及，降温负荷呈现增大的趋势，这对日负荷曲线的影响增大。因此，对该市降温负荷的分析变得越来越重要［2］，也对降温负荷预测模型的准确性提出了更高的要求。

1　负荷特性分析

1.1年负荷特性分析

2011—2014年，该市的供电量、最大负荷以及增长率见表1，本文所用电力数据、图片均来源于该市国家电网公司。由表1可知，该市2012年与2011年相比，售电量基本持平，最大负荷增加6.51%；2013年相对2012年售电量与最大负荷增加明显，增长率分别为8.52%和11.62%；2014年相对2013年两项数据略有回落。

表1　2011—2014年城市年供电量及最大负荷Table 1　Annual urban power supply and its maximum load in years 2011—2014

该市国家电网公司2011—2014年的售电构成见表2。由表2可知，该市大工业售电量接近总售电量的60%，为典型的工业城市；居民用电量近年来持续增长。

省统计局公布的该市2011—2014年的年度经济数据见表3。由表3可知，GDP年增长约200亿元；第二产业对经济增长贡献率从70.8%降为62.7%；第三产业对经济增长贡献率从26.3%增加至34.0%。2014年比2013年的GDP增加了212.5亿元，但年用电量基本持平，第二产业对经济增长贡献率降低了3.7%，可见该城市的产业结构良好。产业结构一定程度上决定宏观经济水平，宏观经济水平一定程度上决定了年供电量［3］。可预见未来几年经济依旧能保持持续增长，售电量将会突破100 TW·h，年最大负荷将突破2 000 MW。

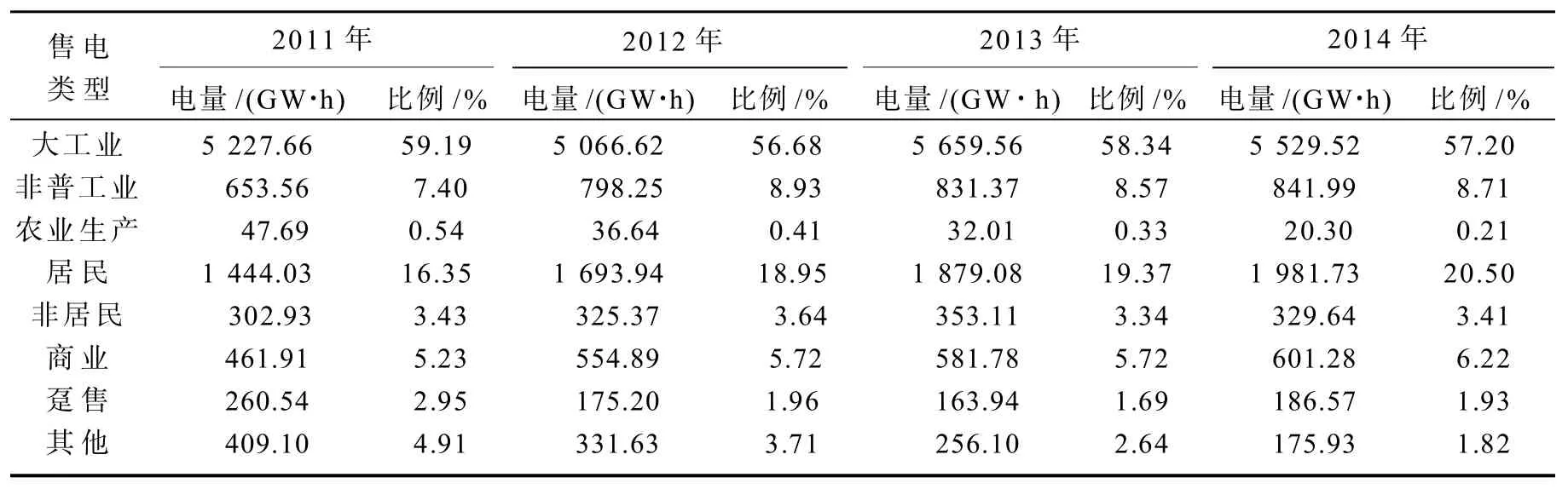
表2　2011—2014年的售电构成Table 2　Composition of power sales in years 2011—2014

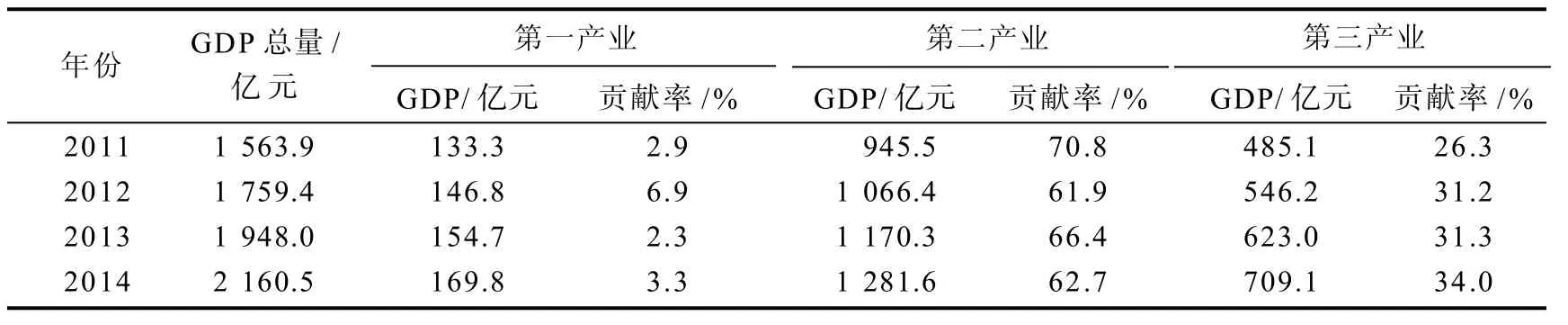
表3　2011—2014年的年度经济数据Table 3　Annual economic data in years 2011—2014

1.2月负荷特性分析

该市电网2011—2014年奇数月的月最大日负荷见表4。

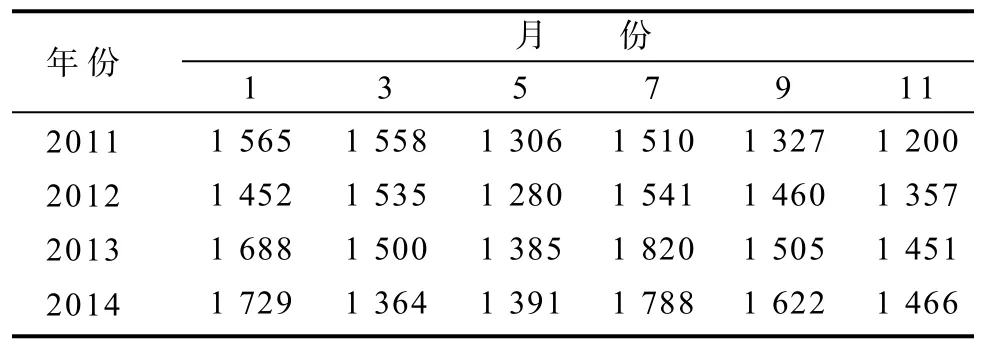
表4　2011—2014年奇数月的月最大日负荷Table 4　Maximum daily load of odd months in years 2011—2014　MW

由表4可知，通常1月、7月的最大日负荷高于其他月份，且增加量远大于其他月份；5月、11月的最大日负荷较小。因为随着居民生活水平的提高，居民越来越愿意在高温高湿或天气寒冷的月份使用空调［4］，使得这类月份的最大日负荷高于气温适宜的月份。

1.3日负荷特性分析

该市的典型日负荷曲线如图1所示。由图1可知，日负荷曲线较为平稳，但在8时、11时、15时、22时左右存在突变；曲线上存在较多毛刺。

工业城市的工业用电方式很大程度上影响着地区负荷曲线的走向［5］。该地区某大型冶炼集团2014年铅锌总产量 64.84 万t，实现营业收入 151.02 亿元，用电量常年占该地区用电量的30%左右，为该地区的工业用电大户，该集团典型日负荷曲线见图2。 该冶炼集团的负荷曲线类似矩形波，高、低用电量过渡时间短、差值大。

参考所在省份峰谷分时电价办法，8时至11时，15时至19时为高峰时段，19时至22时为尖峰时段。显然企业出于节约成本的考虑，避开高峰，尖峰时段的高电价，主动减产，选在电价低的时间段进行生产。工业企业的错峰用电，对地区负荷曲线起到了削峰填谷的作用。

该地区为铁路交通枢纽，铁路车次密集。高速铁路和普通铁路负荷具有负荷峰谷差值大，冲击时间短的特点。能量管理系统（element management system，EMS）显示，某日铁路总加负荷最大值为102.53 MW，最小值为2.95 MW，负荷率为0.41，当日铁路负荷总加曲线见图3。无规律的铁路负荷容易造成地区负荷总加值突然增大，日负荷曲线峰谷值增大，局部母线电能质量下降等问题，对地区电网造成不利影响。

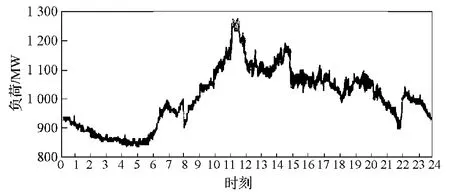
图1　地区典型日负荷曲线Fig. 1　A curve graph of a regional average daily power load

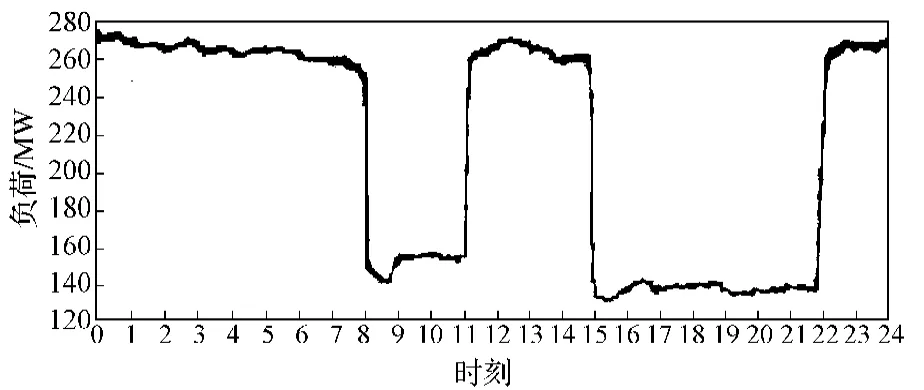
图2　冶炼集团典型日负荷曲线Fig. 2　A curve graph of the average daily power load of metallurgic groups

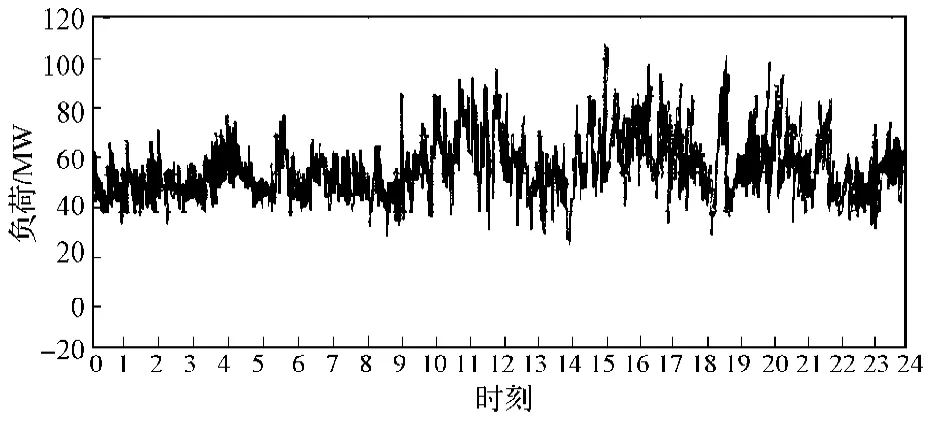
图3　某日铁路负荷总加曲线Fig. 3　A curve graph of the power load of a railway station on a single day

2　降温负荷特性分析

2.1降温负荷计算

因该市地处亚热带季风区，年平均气温为16～18℃，四季分明，有降温采暖需要。随着年售电量的持续增加，以及居民用电比率的提高，尤其是在降温需求高的夏季，降温负荷对日负荷曲线的影响更加明显，因此对降温负荷规律的研究以及预测变得日趋重要。

本文采用基准负荷比较法确定降温负荷曲线，测算过程如下［6］。

1）确定基准日：一般选取天气凉爽，降水量少的月份的某几个工作日，这样的月份几乎没有降温负荷。

2）确定高温日：一般选取一年中平均气温最高的月份为高温月份，在高温月份中选取连续几日温度都在高温范围内的日期作为高温日。

3）确定降温负荷：比较该月中高温日负荷曲线与基准日的负荷曲线，差值即为该日的降温负荷曲线。该月降温曲线的最大值为该年的最大降温的负荷值。

2015年月气温走势见图4。选择7月份作为高温月份，4月作为无采暖无降温的月份，该年中4月与7月的每日气温如图5所示。

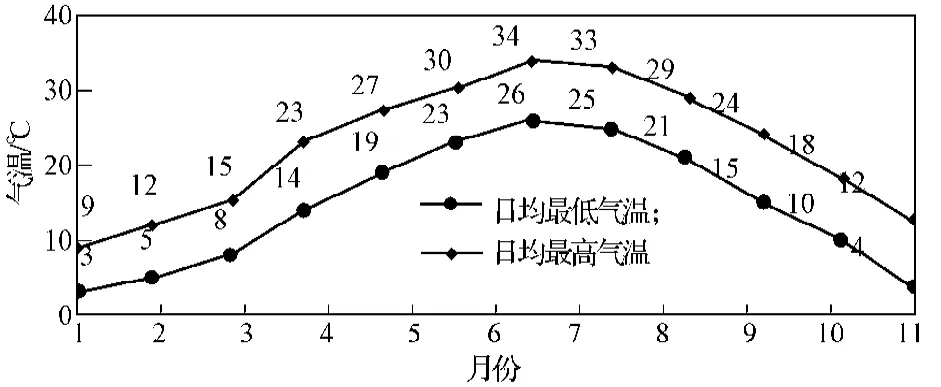
图4　全年气温走势图Fig. 4　Chart patterns for the yearly temperatures

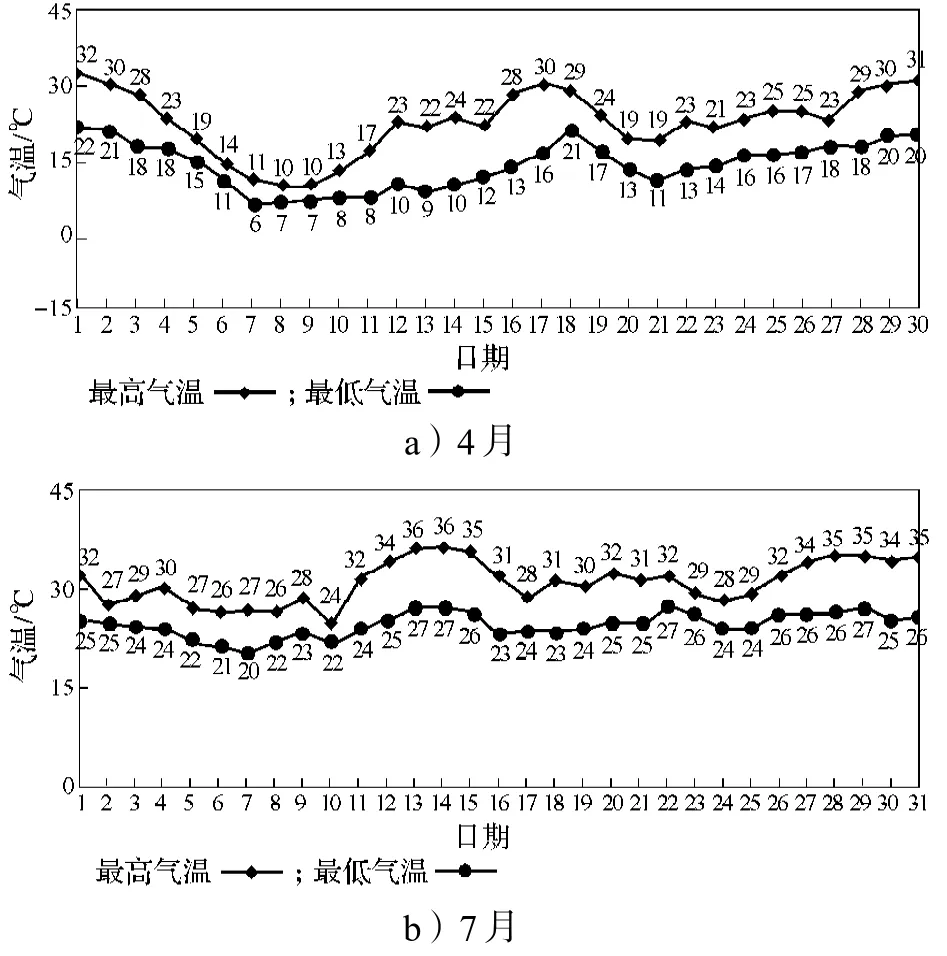
图5　月份日气温Fig. 5　Chart patterns for daily temperatures in April and July

参考月平均气温，选择4月9日，4月15日，4月22日为基准负荷日。本文将最低温不低于24 ℃，最高温不低于34 ℃的日期定为高温日，7月份高温日为：12、13、14、15、28、29、30、31日。考虑该市电网数据采集与监视控制 （supervisory control and data acquisition，SCADA）系统对负荷的记录水平，本文将能量管理系统（element management system，EMS）的历史日负荷数据导出后，按1分钟采样1次，1天选取1 440点进行计算。选取7月15日为高温负荷日，4月15日为基准日，日负荷曲线如图6所示。

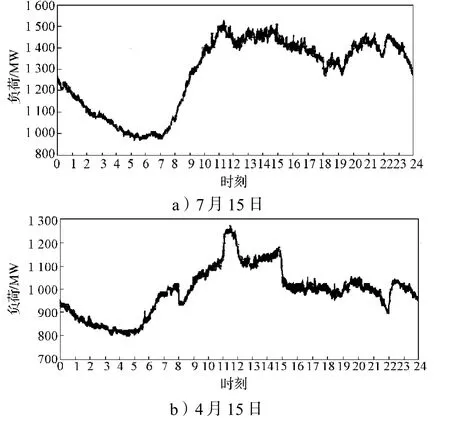
图6　日负荷曲线图Fig. 6　A curve graph of daily power load

对数据进行预处理时，采用一种基于椭圆图形的异常查找方式，同时引入偏最小二乘回归法对历史数据进行提取。从n个历史数据中提取出m个成分，定义为样本i对第h个成分th的贡献率，则

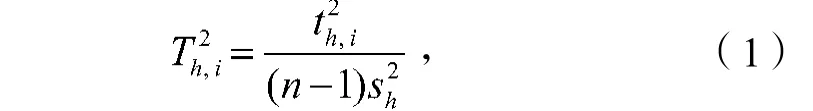
n为样本数。

计算出样本i对成分t1， t2， …， tm的累积贡献率，即

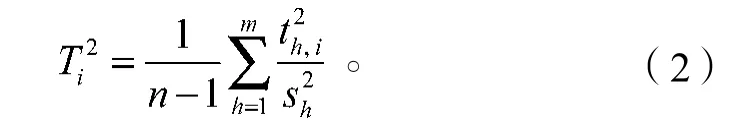
利用统计量

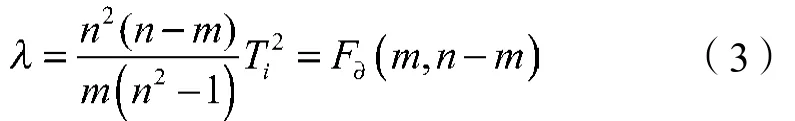
可评估样本对主成分的贡献率。

通常选取2个成分构建函数，判断样本i是否为异常数据，也就是m=2，判别条件为

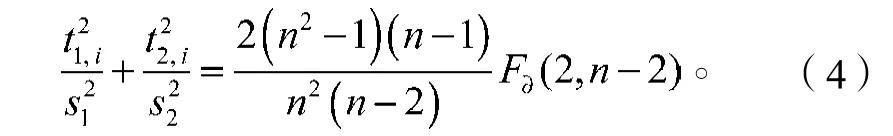
式（4）即为椭圆图形。如果样本点落在椭圆内且远离边界，则认为不是异常数据，落在椭圆外或者靠近边界，则为异常数据。对于异常数据采用三点平滑处理，即

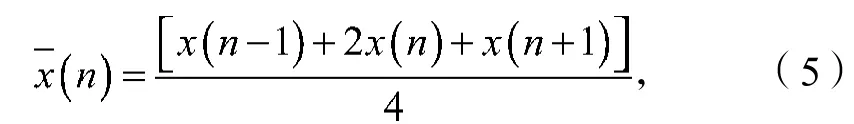
式中：x（n）为异常数据点的数值；

x（n-1）为异常数据点前一点的数值；

x（n+1）为异常数据点后一点的数值；

用MATLAB进行数据处理后，将两日负荷对应时间点的值相减，得出降温负荷曲线，如图7所示。曲线自上而下分别为7月15日负荷曲线、4月15日负荷曲线、降温负荷曲线。

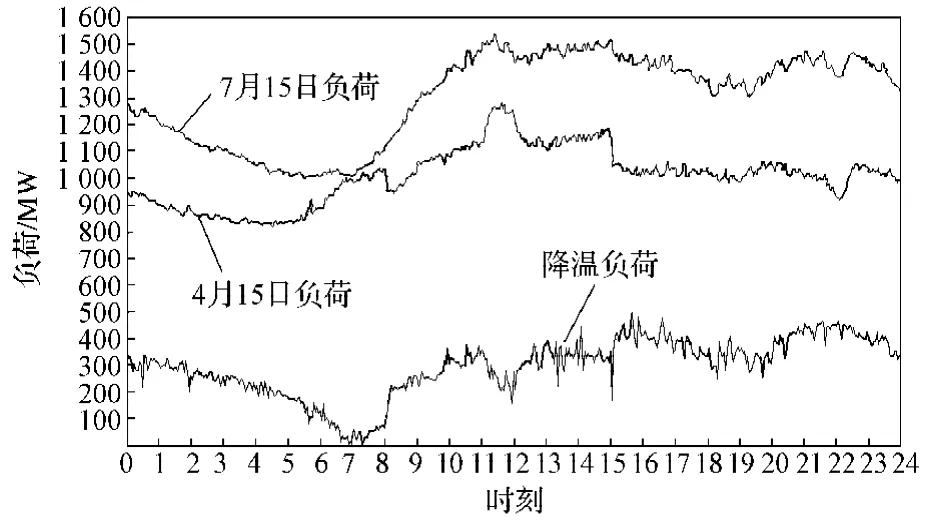
图7　降温负荷曲线Fig. 7　A curve graph of cooling loads

7月份各高温日相对基准日降温负荷最大值见表5，最大降温负荷为513 MW。

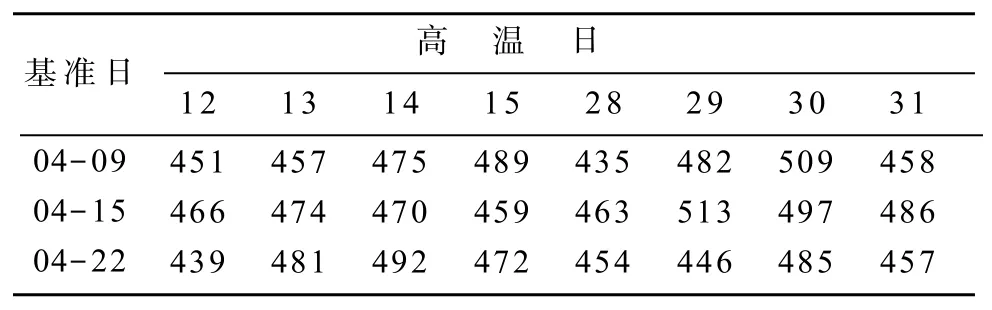
表5　最大降温负荷Table 5　Maximum cooling loads MW

以图7中降温负荷曲线为例，分析多日的降温负荷曲线可知， 8时至11时、15时至23时都存在较高的降温负荷，负荷最高峰出现在16时左右；20时至23时是居民降温负荷高峰时间段，20时至23时降温负荷约为最高降温负荷的85%～92%。这说明居民降温负荷是降温负荷的主要来源。23时至次日8时降温负荷呈下降趋势。参考当地居民生活工作作息时间，以及气温变化规律，23时至次日8时对降温需求不强烈，降温负荷随气温降低而减少。

2.2降温负荷预测

由2.1节的分析可知，降温负荷随时间呈周期性的变化。因此在进行降温负荷预测时，可基于随机序列平稳性的自回归-移动平均（auto-regressive moving average，ARMA）模型理论，假设时间序列是随机产生的，用时间序列的历史数据，进行参数估计后，建立ARMA模型［7］。但在受到如天气突变、设备事故、设备检修等突变因素的影响时，负荷时间序列会出现非平稳的随机过程。因此在ARMA模型基础上用差分计算，将非平稳过程转换为平稳过程，建立累积式自回归-移动平均（auto-regressive integrated moving average，ARIMA）模型，ARIMA模型可适用于非平稳随机时间序列。

ARMA模型结构为

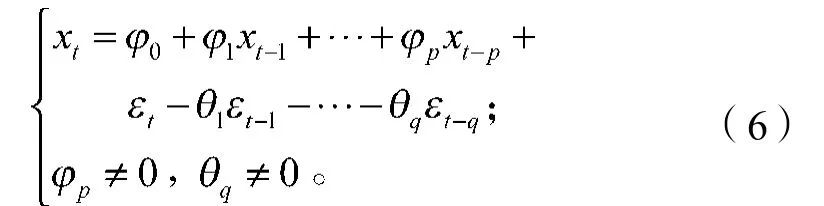
式中：xt为负荷现在值；

xt-1， xt-2， …， xt-p为负荷过去值；

引入延迟算子B，xt-1=Bxt，xt-2=B2xt，…，xt-p=Bpxt，则ARMA模型表示为

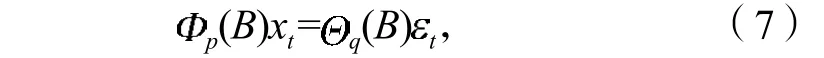
引入xt的一阶差分算子

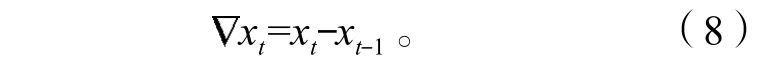
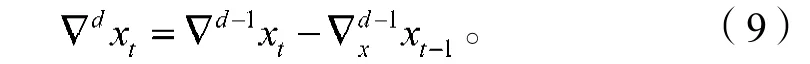
因此，ARIMA模型表示为

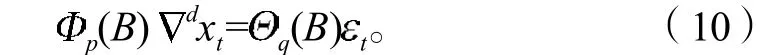
因该模型只考虑了时间序列的变化，对温度变化不敏感。因此，通过改进算法，建立双因子的ARIMA模型，以提高预测精度。

单日气温数据通常包括平均温度、最高温度和最低温度［8］。为分析单日气温数据对降温负荷的影响，建立1个三变量的回归方程

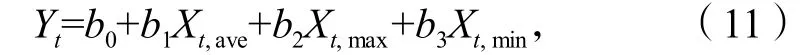
式中：Yt表示最大降温负荷；

t表示日期；

Xt，ave，Xt，max，Xt，min分别表示t日的平均温度、最高温度和最低温度；

b1，b2，b3分别表示平均温度、最高温度和最低温度的回归系数；

b0为常数。

利用MATLAB中的rstool函数，结合表5、图5中的数据进行多元回归拟合。取基准日为4月9日的最大降温负荷值95%的置信区间，通过计算得方程

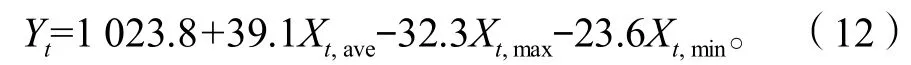
由式（12）可知，平均温度的回归系数的绝对值最大。引入基于平均温度的差分算子T来加强平稳化处理。平均温度的一阶差分算子为

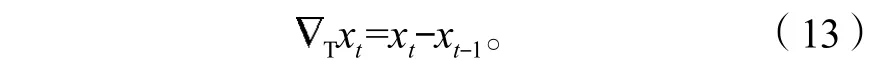
因此，得双因子ARIMA模型

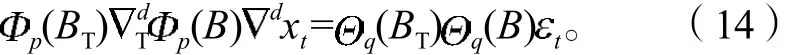
用2015年7月份数据分别拟合ARIMA模型、双因子ARIMA模型，并对8月12日降温负荷进行96个点的预测。采用2种方法预测，得降温负荷曲线如图8所示。由图可知，ARIMA模型在降温负荷拐点处的预测精度不高。用MATLAB软件对2条预测曲线相对实际降温负荷曲线的预测准确度的分析结果为：ARIMA模型预测准确度为92.5%，双因子ARIMA模型预测准确度为97.8%。由此可见，双因子ARIMA模型比ARIMA模型预测准确度更高，对温度影响的处理能力更强。因此双因子ARIMA模型在降温负荷预测方面具有更好的预测效果。

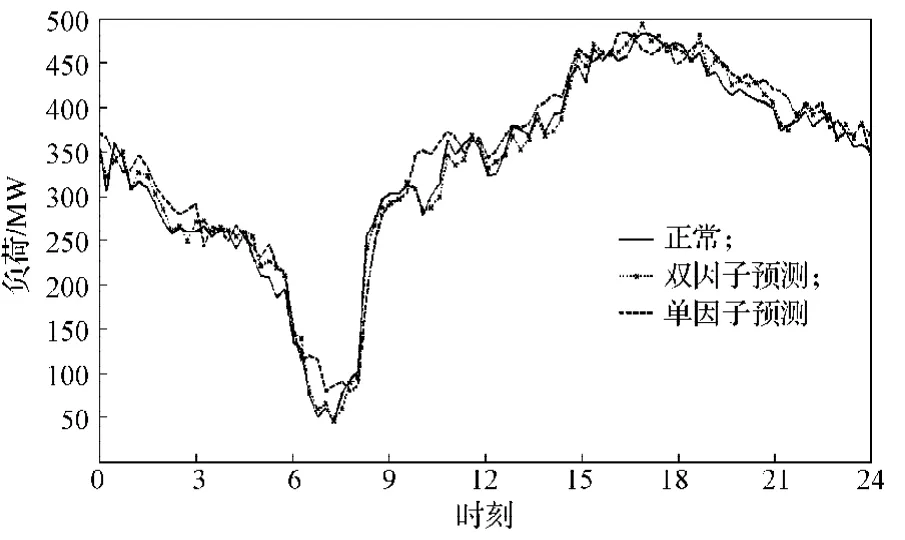
图8　降温负荷预测曲线Fig. 8　A forecasting curve graph of cooling loads

3　结语

本文结合多组数据对某市进行了年、月、日的负荷特性分析，并着重分析了该市的降温负荷。针对采用ARIMA模型预测时，对温度造成的降温负荷影响反应不准确的问题，建立了双因子ARIMA模型，并将2个模型的预测曲线与实际计算得出的降温曲线进行了比较。结果表明，双因子ARIMA模型的预测精度高于ARIMA模型，在降温负荷预测上具有更好的可用性。

［1］兰宇，谭剑中，李轩，等. 地区电网负荷特性研究［J］. 能源技术经济，2010，22（7）：30-35. LAN Yu，TAN Jianzhong，LI Xuan，et al. Study on Regional Power Load Characteristics［J］. Energy Technology and Economics，2010，22（7）：30-35.

［2］薛万磊，温权，单葆国. 降温负荷分析方法研究［J］. 能源技术经济，2011，23（11）：37-40. XUE Wanlei，WEN Quan，SHAN Baoguo. Study on the Analytical Method of Power Load for Cooling［J］. Energy Technology and Economics，2011，23（11）：37-40.

［3］楚成博，刘继东，张利，等. 山东电网夏季降温负荷特性及影响因素分析［J］. 电力需求侧管理. 2013，15（1）：20-24. CHU Chengbo，LIU Jidong，ZHANG Li，et al. Studies on Temperature Lowering Load Regional Characteristics of Shandong Power Network［J］. Power Demand Side Management，2013，15（1）：20-24.

［4］雷铮，张振高，周进，等. 天津电网空调负荷分析与研究［J］. 华北电力技术，2013（2）：12-15. LEI Zheng，ZHANG Zhengao，ZHOU Jin，et al. Analysis and Study on the Air-Conditioning Load of Tianjin Gird［J］. North China Electric Power，2013（2）：12-15.

［5］廖峰，徐聪颖，姚建刚，等. 常德地区负荷特性及其影响因素分析［J］. 电网技术，2012，36（7）：117-125. LIAO Feng，XU Congying，YAO Jiangang，et al. Load Characteristics of Changde Region and Analysis on Its Influencing Factors［J］. Power System Technology，2012，36（7）：117-125.

［6］何晓峰，黄媚，农植贵，等. 地区电网降温负荷与气温的敏感性分析［J］. 电力需求侧管理，2013，15（5）：17-22. HE Xiaofeng，HUANG Mei，NONG Zhigui，et al. Analysis of Cooling Load and Temperature Sensitivity on Regional Grid［J］. Power Demand Side Management，2013，15（5）：17-22.

［7］张素香，赵丙镇，王风雨，等. 海量数据下的电力负荷短期预测［J］. 中国电机工程学报，2015，35（1）：37-42. ZHANG Suxiang，ZHAO Bingzhen，WANG Fengyu，et al. Short-Term Power Load Forecasting Based on Big Data［J］. Proceedings of the CSEE，2015，35（1）：37-42.

［8］任志超，杜新伟，王海燕，等. 调温负荷的估算方法及影响因素研究［J］. 现代电力，2014，31（3）：80-85. REN Zhichao，DU Xinwei，WANG Haiyan，et al. Research on Estimation Method of Temperature Adjusting Load and Its Influence Factor［J］. Modern Electric Power，2014，31（3）：80-85.

（责任编辑：邓光辉）

On an Analytical Approach to Load Characteristics of Urban Power Grids

SUN Xiao1，ZENG Haoyu2，LIANG Wei2，YANG Danqing2
（1. School of Mechanical Engineering，Hunan University of Technology，Zhuzhou Hunan 412007， China；2. School of Electrical and Information Engineering，Hunan University of Technology，Zhuzhou Hunan 412007， China）

A dual-factor auto-regressive integrated moving average model （ARIMA model） has been established to tentatively improve the low accuracy of the ARIMA model in forecasting modern urban cooling loads， followed by a simultaneous predication testing by these two models. A final comparison between the two prediction results shows that the new model， by introducing an average temperature operator to the forecasting process， has effectively improved the urban cooling load forecasting accuracy with a universal applicability on its former basis of an ARIMA model.

power grid；load analysis；load forecasting；ARIMA model

TM714

A

1673-9833（2016）03-0043-06

10.3969/j.issn.1673-9833.2016.03.008

2016-01-05

孙晓（1972-），男，湖南株洲人，湖南工业大学教授，硕士生导师，主要从事机电控制与计算机应用技术方面的教学与研究，E-mail：sxbug@163.com