高层结构中框架柱截面优化设计

唐从青，蒋隆敏

（湖南工业大学 土木工程学院，湖南 株洲 412007）

高层结构中框架柱截面优化设计

唐从青，蒋隆敏

（湖南工业大学 土木工程学院，湖南 株洲 412007）

阐述了框筒结构优化设计基本理论，探讨了运用ANSYS软件进行框筒结构优化设计的有关方法。以某18层框筒结构办公楼为例，先进行柱截面优化设计，再对优化后的设计模型在地震波作用下进行抗震变形验算与分析。研究结果表明，优化设计后不仅可使柱子成本降低28.168%，而且框筒结构的弹性层间位移角仍然满足抗震性能要求。

柱截面；框筒结构；优化设计；地震波；弹性层间位移角

1　研究背景

房屋结构设计的主要设计理念是，在保障房屋实用、安全、经济、美观的前提下，达到空间的最优配置，实现资源的最佳利用［1］。而结构优化设计正是从许多可行设计中，以目标函数（设计指标）为基础，找出这个函数的极值（极小值或极大值），从而选出最优设计方案［2］。即根据建筑与结构规范或某些特定条件优化建筑结构设计，使某种指标（如质量、面积、体积、应力、费用等）达到最佳配置。从已有经验看，与传统设计相比，运用优化设计可以使工程造价降低5%～30%［3］。这种工程结构优化设计由“分析与校核”发展为“综合与优选”，从而有利于提高工程结构的经济效益。

框筒结构是将剪力墙布置而成的薄臂筒和密柱框架两者结合起来，取长补短，共同抵抗水平荷载的结构体系。钢筋混凝土框筒结构的剪力墙部分能明显增大结构抗侧刚度和抗扭刚度，而框架部分能给建筑提供灵活使用空间，并且两者结合能发挥协同作用。因此框筒结构已成为我国高层建筑的重要结构形式之一，并且在未来仍将有美好的发展前景。

国内关于框筒结构的研究主要是在加强层不同位置对框筒结构的影响， 核心筒墙体面积占核心筒平面面积的不同比值对框筒结构的影响，框筒楼板不同开洞率对框筒结构的影响等方面。国外关于框筒结构的研究主要是在钢筋混凝土框架核心筒结构的抗震性，结构的耐撞性，结构曲面优化，结构体系整体分析等方面。国内外对框筒结构分单元进行柱截面尺寸优化方面的研究较少。

在已有的钢筋混凝土超高层框-筒结构体系的优化［4］中，其结构优化所涉及的设计变量较多，所采用的优化法收敛速度较快、优化效果好，优化后的结构体系能有效节约投资成本。该结构体系的优化说明了进行框筒结构柱截面优化设计是可行的，同时也为框筒结构柱截面优化设计提供了参考依据。

对框筒结构分单元进行柱截面尺寸优化方面的研究较少，而框筒结构的框架柱造价占总造价的比例较大，高层结构柱截面尺寸进行分段缩小方面的结构设计较普遍且实用性强，因此对高层框筒结构柱截面优化设计具有重要的实际意义。

2　优化设计的数学模型

建立数学模型是将工程实际问题用数学表达式表示，包括选定设计变量和状态变量、选择目标函数、建立约束方程等内容［2］。

给定参数是指描述结构特性时某些给定的参数。在优化过程中，给定参数可以作为常数考虑，其值是固定的。如最大应力值、最小应力值、柱高、材料重度及弹性模量等，一般属于给定参数。

设计变量是指优化设计中待确定的某些参数［2］。一个结构的优化设计可以由某个量或若干个量来描述，这些量可以是结构的几何参数，如高度、间距和跨度等，也可以是结构构件的截面尺寸和材料的弹性模量等。

状态变量是指控制设计的因变量［5］。状态变量指的是应力、变形、频率等。运用ANSYS软件进行结构优化分析，一般的状态变量必须是ANSYS可以计算的数值。在特定条件下，任何参数都能定义为状态变量。

目标函数是设计指标达到最小化或最大化的函数［1］。结构的刚度、造价、重度、自振频率等目标函数代表结构优化设计的某个重要指标。以结构的刚度作为目标函数，最终的目的是寻求它的极大值；而以结构的造价、重度为目标函数，其目标就是求出它们的极小值；如果将自振频率作为目标函数，使结构的自振频率避开水平风荷载、地震荷载、吊车荷载等动力荷载下结构的固有频率，从而避免结构在动力荷载作用下发生共振而损坏。

约束条件是指优化设计寻求目标函数极值时的某些限制条件［2］。结构优化的数学模型是通过计算机计算而得到的设计参数，并且应符合以下2个条件：第一个是约束条件，如结构构件的截面应力不超过容许值；第二个是设计变量，如结构的截面尺寸、间距、跨度等，设计变量在优化后达到最小化或最大化。

本文以某18层框筒结构办公楼为例，运用有限元软件ANSYS进行结构柱截面优化设计。该结构布置具有对称性，结构受力也具有对称性，因此只取框筒结构左半部分进行优化分析。以左半部分每上下相邻3层作为1个单元，共6个结构单元，从而将每根柱子分成6段，取每段柱顶端为控制点，则每根柱子共6个控制点。设第i根柱子6个控制点处正方形柱截面边长分别为Hi1， Hi2， Hi3， Hi4， Hi5， Hi6，其中i表示柱子编号，i=1， 2， …， 9，具体编号如图1所示。使用PLANE 42元素对柱子做2D分析，取每根柱截面的最大和最小的轴向应力作为状态变量，其中最大轴向应力为SMAX，最小轴向应力为SMIN，SMAX、SMIN的取值分别为N0及-N0， N0的计算公式见式（1）。将柱子的总造价（SCOST）作为目标函数。优化后框筒结构每段柱截面均取等截面，每段柱的截面边长取优化后对应的控制点处柱截面边长的值，分别为hi1， hi2， hi3， hi4， hi5， hi6。在其余条件相同的情况下，以优化后柱截面尺寸重新建立框筒结构模型，并计算分析。

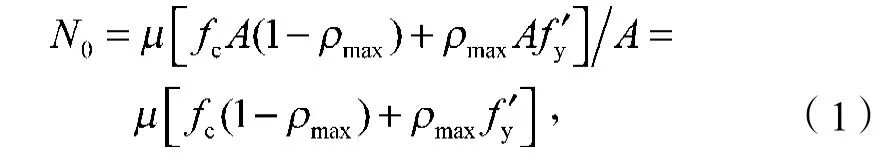
fc表示混凝土抗压强度设计值；

A表示柱截面面积；

综上所述，设计优化问题可表示成如下数学模型。

Minimize ：SCOST

Subject to ：

-N0≤ SMAX ≤N0，-N0≤ SMIN≤N0，

500 ≤ Hi1≤1 100， 500 ≤ Hi2≤1 100，

500 ≤ Hi3≤1 100， 500 ≤ Hi4≤1 100，

500 ≤ Hi5≤1 100， 500 ≤ Hi6≤1 100，

hi1=MAX （Hi0）， hi2=MAX （Hi1），

hi3=MAX （Hi2）， hi4=MAX （Hi3），

hi5=MAX （Hi4）， hi6=MAX （Hi5），

Hi0=1 100， i=1， 2， 3， 4， 5， 6， 7， 8， 9。

3　算例

某18层框筒结构办公楼，建筑物呈U形，总宽16 m，总长44 m，层高3 m，总高54 m。结构平面布置如图1所示，尺寸标注均为mm。根据房屋结构在地震作用下的实例算法［7］，运用ANSYS有限元分析软件进行建模，框架梁、柱单元采用Beam 188单元，剪力墙、楼板采用Shell 63单元，框筒结构的整体模型如图2所示。

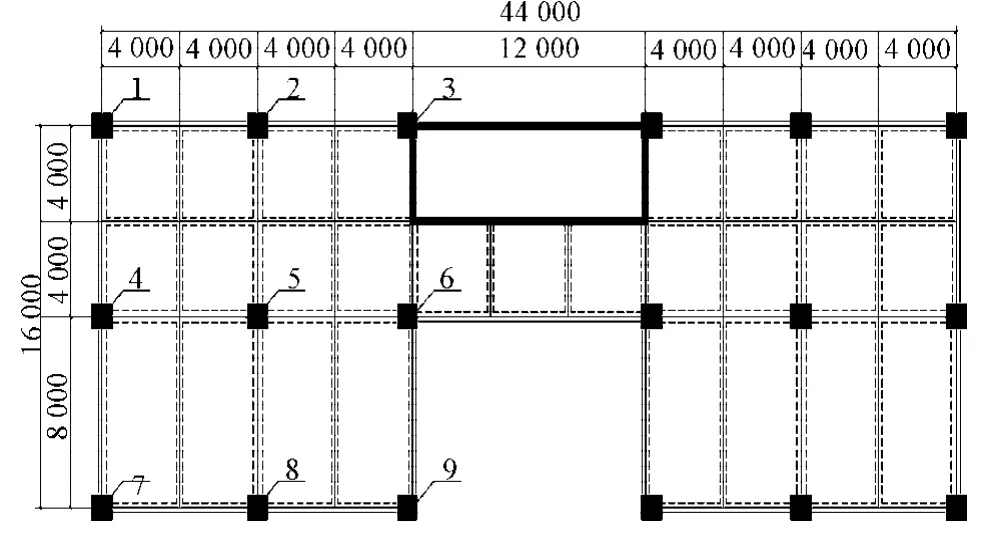
图1　结构平面布置图Fig. 1　Structure layout

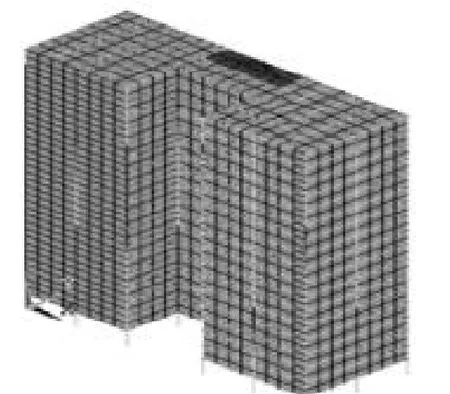
图2　框筒结构的整体模型Fig. 2　An integrated model for frame-tube structures

根据GB 50009—2012《建筑结构荷载规范》［8］对框筒结构模型施加荷载及约束，再根据框筒结构在地震作用下各层柱子的轴压比限值［9］，反算出框筒结构柱子的抗压强度允许值。优化分析时，以柱子的抗压强度允许值作为约束条件，以各段柱子的截面尺寸作为设计变量，以柱子总造价作为目标函数，以框筒结构弹性层间位移角限值作为优化后结构的校核条件，同时兼顾经济性、安全性和实用性。首先运用ANSYS软件对框筒结构的初始设计模型在地震作用下进行分析，根据约束条件和设计变量进行评估，然后对设计进行修正。再重复执行分析-评估-修正的循环过程，直到所有设计变量和目标函数都满足要求，从而得到最优设计方案。优化前后柱截面尺寸见表1，优化前后柱子造价见表2。

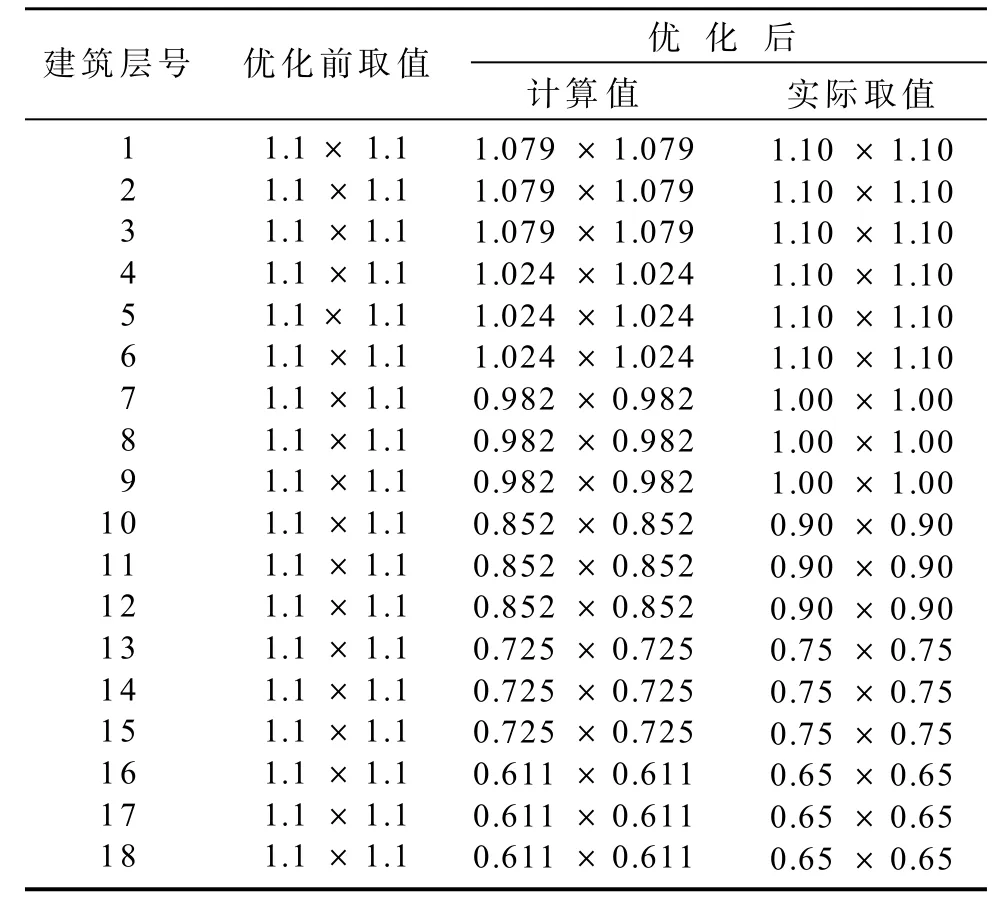
表1　优化前后柱截面尺寸对照表Table 1　Cross-reference of sizes between optimized and non-optimized column cross-sections m2

表2　优化前后柱子造价对照表Table 2　Cross-reference of the budgets between optimized and non-optimized concrete columns

由表2中的数据通过计算可知，经过框筒结构柱子截面尺寸的优化设计后，柱子总造价降低了28.168%。

4　抗震变形验算与分析

结构优化分析与设计不是以牺牲结构安全和抗震性能来求得经济效益，而是将结构理论和先进技术进行有机结合。根据设计要求和工程实践经验，以结构设计规范为限制条件，并以造价为目标，利用数学方法对设计进行调整与改进，从而找出满足预定要求的最佳设计方案。首先运用ANSYS中Array Parameters定义多遇地震波数据矩阵，分别输入x方向、y方向地震波，对原结构模型进行优化设计；再对优化设计后的结构模型进行抗震变形验算与分析，得出楼层不同方向层间最大位移与层高的比值（弹性层间位移角）。不同方向的地震波见图3，优化后楼层不同方向层间最大位移与层高的比值见图4。

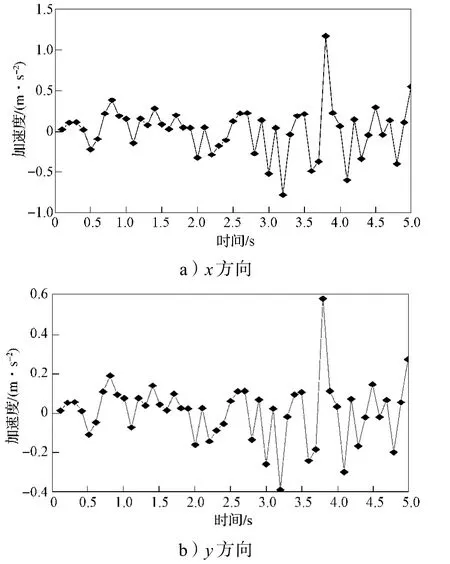
图3　不同方向的地震波Fig. 3　Seismic waveform registered in different directions

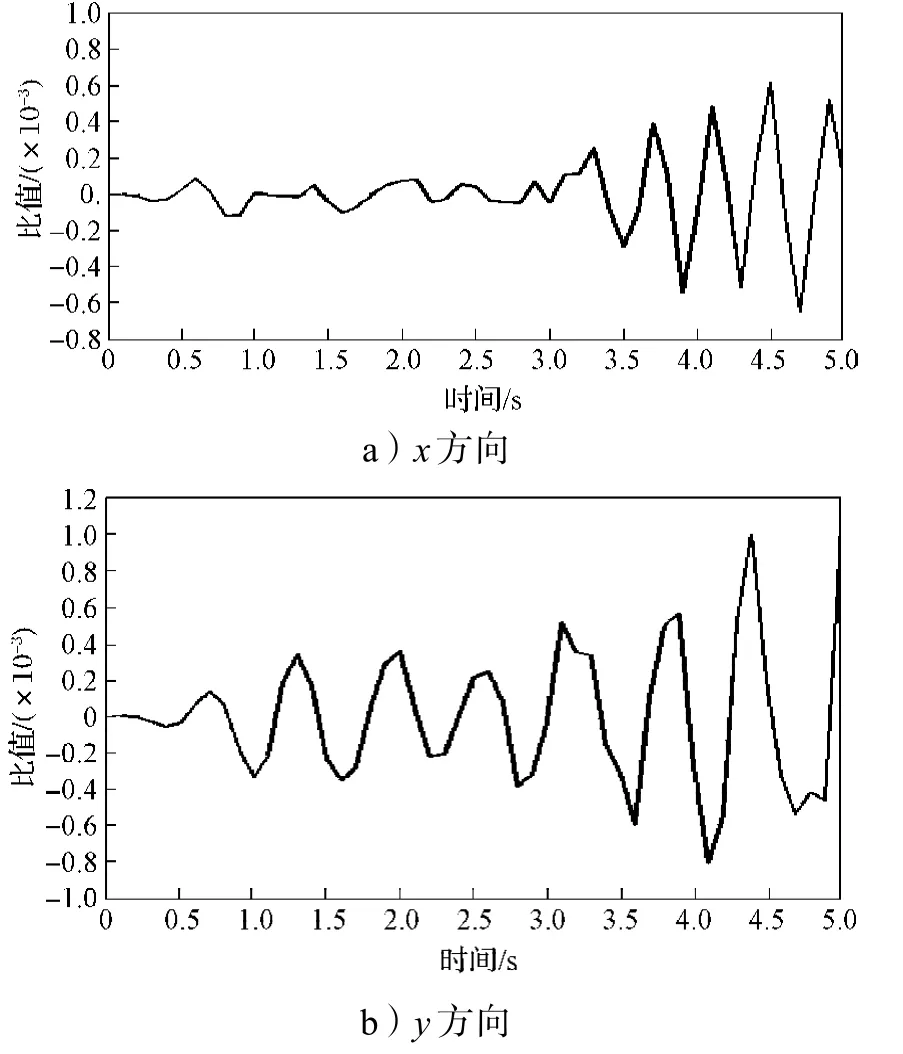
图4　优化后楼层不同方向层间最大位移与层高的比值Fig. 4　The ratio of the maximum inter-laminar displacement in different directions and the height of optimized high-rise structures

对图4进行分析，可以得出优化后的楼层层间最大位移与层高的比值的最大值为0.001 05，而框筒结构弹性层间位移角限值为1/800（0.001 25）。因0.001 05小于0.001 25，这满足框筒结构弹性层间位移角限值1/800的要求［10］。因此，对框筒结构柱子截面尺寸进行优化设计后，在多遇地震作用下，框筒结构不仅在抗震性能方面有保证，而且降低了造价，减轻了自重。

5　结论

本文对高层结构中框架柱截面的优化设计进行了研究，可得如下结论。

1）以地震作用下框筒结构柱子的轴压比限值为条件，反算出柱子的抗压强度允许值；以抗压强度允许值、柱子的截面尺寸、柱子总造价、弹性层间位移角限值作为计算参数，对柱截面进行优化。这样可使柱子成本降低28.168%，也说明了该优化设计方法的实用性。

2）本文的优化设计减小了柱截面尺寸并使多层模板尺寸相同，从而能满足流水施工的要求。这样不仅降低了房屋造价，减轻了结构自重，而且抗震变形验算结果符合规范要求，也说明了优化设计方法的可行性。

［1］王鹏. 建筑结构设计优化方法在房屋结构设计中的实际应用分析［J］. 中国建材科技，2014（4）：162-163. WANG Peng. Analysis of the Practical Application of Building Structure Design Optimization Method in Structural Design of Building［J］. China Building Materials Science & Technology，2014（4） ：162-163.

［2］高新艳. 框架结构优化设计与地震波瞬态分析［J］. 建材技术与应用，2011（11） ：11-13. GAO Xinyan. Frame Structure Optimization Design and Transient Analysis of Seismic Waves［J］. Research & Application of Building Materials，2011（11） ：11-13.

［3］张炳华，侯昶. 土建结构优化设计［M］. 上海：同济大学出版社，1998：1-2. ZHANG Binghua，HOU Chang. Optimum Structural Design［M］. Shanghai：Tongji University Press，1998：1-2.

［4］徐荣. 钢筋混凝土超高层框-筒结构体系的优化［D］.武汉：华中科技大学，2006. XU Rong. Optimum Design of Reinforced-Concrete Super High-Rise Frame-Tube Structure System［D］. Wuhan：Huazhong University of Science and Technology， 2006.

［5］蔡新，郭兴文，张旭明. 工程结构优化设计［M］. 北京：中国水利水电出版社，2003：3-6. CAI Xin，GUO Xingwen，ZHANG Xuming. Optimization Design of Engineering Structure［M］. Beijing：China Water Conservancy and Hydro-Power Press，2003：3-6.

［6］中国建筑科学研究院. 混凝土结构设计规范 ：GB 50010—2010［S］. 北京：中国建筑工业出版社，2010：123. China Academy of Building Research. Code for Design of Concrete Structures：GB 50010—2010 ［S］. Beijing：China Architecture & Building Industry Press，2010：123.

［7］王金龙. ANSYS 12.0土木工程应用实例解析［M］. 北京：机械工业出版社，2011：67-89. WANG Jinlong. ANSYS 12.0 Application Case Analysis of Civil Engineering［M］. Beijing：China Machine Press，2011：67-89.

［8］中国建筑科学研究院. 建筑结构荷载规范：GB 50009—2012［S］. 北京：中国建筑工业出版社，2012：14-22. China Academy of Building Research. Load Code for the Design of Building Structure：GB 50009—2012［S］. Beijing：China Architecture & Building Industry Press，2012：14-22.

［9］中国建筑科学研究院. 高层建筑混凝土结构技术规程：JGJ 3—2010［S］. 北京：中国建筑工业出版社，2010：66. China Academy of Building Research. Technical Specification for Concrete Structures of Tall Building：JGJ 3—2010［S］. Beijing ：China Architecture & Building Industry Press，2010：66.

［10］中国建筑科学研究院. 建筑抗震设计规范：GB 50011—2010［S］. 北京：中国建筑工业出版社，2010：44. China Academy of Building Research. Code for Seismic Design of Buildings：GB 50011—2010［S］. Beijing：China Architecture & Building Industry Press，2010：44.

（责任编辑：邓光辉）

An Optimized Design for the Column Cross-Section of Frameworks in High-Rise Structures

TANG Congqing，JIANG Longmin
（School of Civil Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

This paper expounds the basic theory of optimizing designs for frame-tube structures and explores methods of achieving this goal with the application of ANSYS software. With an 18-storeyed office building in the frame-tube structure as the research subject， the procedures begin with an optimized design for the column cross-section， followed by the computation and analysis of the elasto-plastic capability of optimized design models under the action of seismic waves. The findings show that the optimized design models for the column cross-section could reduce the cost of concrete columns by 28.168%. What's more， the elastic inter-laminar displacement angle of the frame-tube structure still comes up to the anti-seismic standard all the same.

column cross-section ；frame-tube structure ；optimized design ；seismic waves ；elastic inter-laminar displacement angle

TU375.3

A

1673-9833（2016）03-0008-04

10.3969/j.issn.1673-9833.2016.03.002

2016-02-28

国家自然科学基金资助项目（51058001）

唐从青（1989-），男，湖南怀化人，湖南工业大学硕士生，主要研究方向为新型材料在结构加固中的应用，E-mail：546709579@qq.com