时变线性系统的系统建模与虚拟仿真教学

杨宗长



时变线性系统的系统建模与虚拟仿真教学

杨宗长[1]

（湖南科技大学 信息与电气工程学院，湖南 湘潭 411201）

时变线性系统是信息处理相关课程教学的扩展内容，而其解往往不能写成解析解的形式，因而其数值解法是教学与科研中的一个基本问题．利用状态空间分析法，以实现对时变线性系统的系统建模，利用计算机虚拟仿真技术，可直观便捷地完成系统的虚拟仿真并得到其系统响应的数值解．在Matlab/Simulink图形交互式之虚拟仿真环境中，进行了时变线性系统的系统建模与虚拟仿真设计与实验．实验结果表明，其仿真建模过程直观明了，可操作性强，求解方法便捷可行．

计算机化教学；线性时变系统；虚拟仿真；Matlab/Simulink；数值求解

理想的线性时不变系统（Linear Time-invariant Systems，LTIS），是信号与系统课程教学内容中一个核心概念[1-5]．而现实世界以及工程实践中，时变线性系统或称线性时变系统（Linear Time-variant Systems， LTVS）亦更为常见．因而在科学研究和工程应用中，求解时变线性系统（LTVS）非常重要．同时在信号与系统课程教学中，引入时变线性系统（LTVS）的相关教学内容亦非常必要．而时变线性系统（LTVS）的解往往不能写成解析解的形式，因而数值求解法对于线性时变系统（LTVS）非常重要．随着计算机技术的快速发展和广泛应用，计算机仿真（Computer-based simulation，CBS）[6-8]为科学研究以及工程应用领域中众多问题的求解，提供了一种强有力的工具．利用状态空间分析法和计算机虚拟仿真技术，可以便捷直观地实现对时变线性系统建模及其系统响应之数值求解．

目前，由美国Mathworks公司发布的Matlab[9]成为了当今国际主流的科学计算与仿真软件之一．在其Simulink的虚拟仿真环境中，它提供了面向众多科学与工程领域的相关功能模块，可对目标系统进行有效准确的系统建模以及虚拟仿真，并得到其数值解．设给定某时变连续时间系统，在任意输入信号作用下，如何计算求解其系统响应是教学与科研中的一个基本问题．由于时变线性系统（LTVS）的解往往不能写成解析解的形式，因而用于求解线性时不变系统（LTIS）之时域经典和变换域之解析解方法，已不适用，且较繁琐．因而非常适合在Matlab/Simulink虚拟仿真计算环境中，利用状态空间分析法，首先实现对时变线性系统的系统建模，然后利用Simulink虚拟仿真模块，可直观便捷地完成系统的虚拟仿真并得到其系统响应的数值解．

1 时变线性系统的解

对于时变线性系统，设其状态空间表达式为

可知其满足普希茨（lipschitz）条件[10-11]，即

因而，时变线性系统的解存在且解唯一．

那么，由式（1）和式（3）可得

如此，即得到该时变线性系统之等价系统为

此时，由式（5）和式（6），可得

并可进一步得到

至此，可知时变系统之求解过程比较繁杂，且其解往往不能写成解析解的形式．因而在教学与工程应用中，数值求解法对于时变系统非常重要．随着信息技术的发展与应用，计算机仿真技术为时变系统的数值求解提供了一种高效便捷的途径．

2 时变线性系统之建模方法

（1）将微分方程左端只保留输出信号的最高阶导数项，即可得

（2）基于状态空间分析法，然后选择一组简单的状态变量，即

（3）由式（11）~（13），可得该微分方程对应的一阶微分方程组

（4）根据式（14），对于该时变线性系统，可得到其建模仿真实现框图（见图1）．

内蒙古伊利实业集团紧抓“一带一路”带来的历史机遇，筹划建立“全球智慧链”。“全球智慧链”通过整合全球的优质自然资源、全球标准、人才等，实现跨越全球的智慧共享与碰撞。目前，伊利已投资建设新西兰大洋洲乳业生产基地、设立伊利欧洲研发中心、主导实施中美食品智慧谷，并与新西兰林肯大学展开全产业链研发合作。

同时，对于式（14）所列的一阶微分方程组，可将其写成矩阵向量表述方式

此即为系统的状态空间表达式．同理，更一般地，对于类似高阶时变线性系统，亦用其状态空间表达式来描述，并得到其系统仿真实现框图（类似图1）．

3 时变线性系统之仿真设计与分析

Matlab提供了功能齐备的集成计算环境．在其图形交互式之模型输入的计算仿真环境Simulink中，它提供了面向众多科学与工程领域的相关功能模块，允许用户用框图的形式进行系统建模和虚拟仿真，以得到系统的数值解．

以变线性连续系统（式（16））为例，基于状态空间分析法之建模方法，利用Matlab/Simulink模块库中的相关功能模块：信号模块、积分模块、比例器（增益）模块、时钟模块、Matlab函数模块以及乘法器模块、加法器模块和示波器等，设计并搭建完成该系统的虚拟仿真模型，然后仿真运行以得到其系统响应的数值解．

使用Matlab/Simulink仿真环境选取合适相关功能模块，搭建完成其系统仿真模型（见图2）．

根据给定的时变线性系统及其初始条件，完成仿真模型的参数设置（见图3）．仿真运行，求解其系统响应之数值解，结果见图4．

在Simulink 中添加“输出（Output）”模块（见图2），可输出其系统响应的数值解到工作区或保存到文件，便于进一步应用或分析．更进一步，对于更一般的时变系统（注：时变线性系统属于时变系统的子类），也进行类似的建模仿真以及求解其系统响应．

例如：著名的 Van der Pol 方程是典型数理表达式中的基本方程，代表了一类极为典型的非线性问题[12-13]

Van der Pol 方程亦无法精确求得其解析解，故研究者们一直在努力地寻找或改进其近似解的求解方法，诸如扰动法，KBM法，多尺度法，谐波平衡法，以及将扰动法和谐波平衡法相结合之等效小参量法等．文献[12]给出其解的若干（）图示（见图5，注：图5中其因变量为，自变量用表示，而本文中其自变量表示为）．

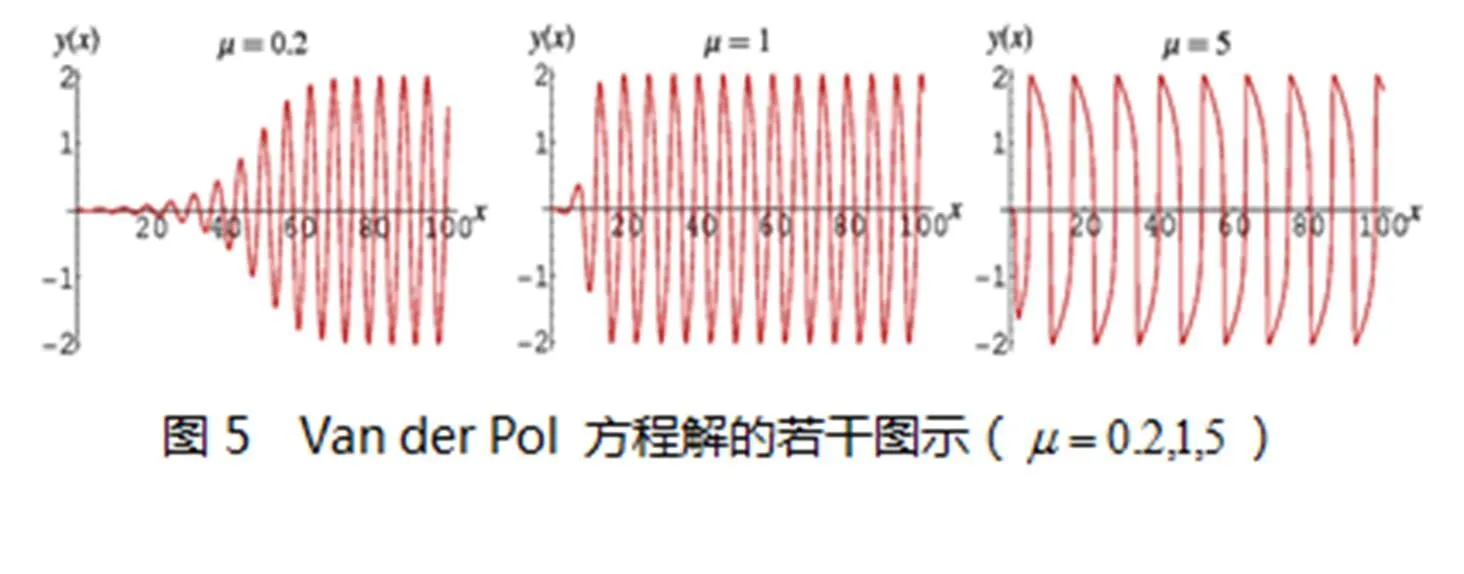
参照图5可知，虚拟仿真所得的系统响应之数值解结果（见图6~9）有效可行．同时，相比于其他方法诸如：扰动法，KBM法，多尺度法，谐波平衡法以及等效小参量法等，本文提出的基于计算机仿真技术的系统建模与虚拟仿真过程（见图6）直观明了，人机交互性更强，实现方法便捷直观．由此可见，在诸如Matlab/Simulink图形交互式仿真环境中，可以很便捷地构建完成时变系统的虚拟仿真模型，然后仿真运行以得到其系统响应的数值求解，并可对结果进行保存或供进一步分析．

4 结束语

在电子信息类专业基础课程信号与系统的教学过程中，相对于经典的线性时不变系统（LTIS），时变线性系统或称线性时变系统（LTVS），是课程教学的一个重要拓展内容．因为在现实世界以及工程实践中，时变线性系统更为常见．由于时变线性系统（LTVS）的解，往往不能写成解析解的形式，因而传统用于求解线性时不变系统（LTIS）之时域经典和变换域之解析解方法，对于时变线性系统（LTVS）而言，显然已不适用，且其求解过程比较繁杂．图形交互式的计算仿真环境如Matlab/Simulink的出现，为LTVS系统以及更一般的时变系统的仿真建模及其系统响应的数值求解提供了便捷直观的途径．

根据给定的时变系统以及初始条件和输入信号，基于状态空间分析法，以实现对时变线性系统的系统建模，然后利用计算机虚拟仿真技术，来完成系统的虚拟仿真以得到系统响应的数值解．同时，在诸如Matlab/Simulink科学计算与虚拟仿真环境中，可以很便捷直观地完成系统建模与虚拟仿真，并得到系统响应的数值解．由此可见，计算机仿真技术在时变系统分析中的必要性、辅助性以及便捷性．虚拟仿真实验及其系统响应的数值结果表明，基于计算机仿真技术的时变线性系统的系统建模与虚拟仿真过程直观明了，可操作性强，实现方法便捷有效，值得在教学与科研中进行推广和应用．

[1] 郑君里，应启珩，杨为理．信号与系统[M]．3版．北京：高等教育出版社，2011

[2] 陈后金．信号与系统[M]．北京：清华大学出版社，2003

[3] 管致中，夏恭恪，孟桥．信号与线性系统[M]．4版．北京：高等教育出版社，2004

[4] 曾禹村，张宝俊．信号与系统[M]．北京：北京理工大学出版社，2002

[5] Oppenheim A V．Signals and Systems中译本[M]．西安：西安交通大学出版社，2001

[6] Orion Zavalani．Computer-based simulation development of a design course project in electrical engineering[J]．Computer App-lications in Engineering Education，2015，23（4）：587-595

[7] VAHIDI B，ESMAEELI E．MATLAB-SIMULINK-based simulation for digital differential relay protection of power transformer for educational purpose[J]．Computer Applications in Engineering Education，2013，21（3）：475-483

[8] Recai Kilic，Fatma Yildirim Dalkiran．Utilizing SIMULINK in modeling and simulation of generalized chaotic systems with mul-

tiple nonlinear functions[J]．Cmputer Applications in Engineering Education，2010，18（4）：684-693

[9] 薛定宇．控制系统计算机辅助设计——MATLAB语言与应用[M]．2版．北京：清华大学出版社，2012

[10] Robert E，Skelton．Dynamics Systems Control：linear systems analysis and synthesis[M]．New Jersey：John Wiley Sons，1988

[11] Robert E，Skelton T，Iwasaki，et al．A Unified Algebraic Approach to Control Design[M]．Oxfordshire：Taylor & Francis，1997

[12] Weisstein，Eric W．Van der Pol Equation[EB/OL]．（1999-01-01）[2016-01-01]．http//mathworld.wolfram.com/vanderPol

Education.htlm

[13] 李献礼，谭晓玲，丘水生，等．Van der Pol 方程分析研究的新结果[J]．大学物理，2005，24（6）：16-19

Teaching study on simulation-based numerical solution for system response of the linear time-variant system

YANG Zong-chang

（School of Information and Electrical Engineering，Hunan University of Science and Technology，Xiangtan 411201，China）

It is usually difficult to obtain analytical solutions for the linear time-variant system（LTVS）which is an extended content in signal processing courses，and then numerical methods of the LTVS is one basic issue in science and teaching．Based on the state space analysis，modeling and virtual simulation for a LTVS as well as its numerical solution for system response can be achieved in one convenient and vivid way by employing the basic blocks in the Matlab-Simulink．The Simulink-based simulations show workability of the presented method.

CAI；LTVS；virtual simulation；Matlab/Simulink；numerical solution

G434

A

10.3969/j.issn.1007-9831.2016.04.018

2016-01-05

湖南省科技厅计划项目（2013GK3090，2015JC3111）；湖南省教育厅科研项目（11A036）

杨宗长（1972-），湖南怀化人，副教授，博士，主要从事信息处理与应用数学建模，通信与信息系统研究．E-mail：yzc233@163.com

1007-9831（2016）04-0065-06