基于脉冲调整的四桥臂逆变器死区补偿策略

周　娟　陈　映，2　唐慧英　魏　琛　吴　璇

(1.中国矿业大学信息与电气工程学院　徐州　221008 2.四川电力设计咨询有限责任公司　成都　610041)



基于脉冲调整的四桥臂逆变器死区补偿策略

周娟1陈映1，2唐慧英1魏琛1吴璇1

(1.中国矿业大学信息与电气工程学院徐州221008 2.四川电力设计咨询有限责任公司成都610041)

为防止桥臂直通加入死区时间会导致逆变器输出能力下降以及输出波形畸变，需要进行死区补偿。四桥臂逆变器开关状态多，电压矢量分布复杂，死区补偿实现困难。对死区效应及其产生机理进行分析，归纳各相电流极性与对应脉冲调整方案的关系，将基于脉冲调整的死区补偿策略应用于四桥臂逆变器。该补偿策略在同一电流极性下脉冲调整具有一致性，易于实现，仅需判断电流极性即可确定脉冲调整方案，达到校正基矢量作用时间的目的，补偿死区效应。分别在三相平衡及不平衡工况下对基于脉冲调整的四桥臂逆变器死区补偿策略进行仿真和实验分析，结果表明该补偿策略能提高逆变器输出能力，减小波形畸变程度，有效补偿了死区效应。

四桥臂逆变器三维空间矢量脉宽调制死区补偿脉冲调整

0　引言

与三相三桥臂逆变器相比，四桥臂结构的开关状态由8个增加到16个，其控制自由度大、输出电流纹波小、中线电流控制灵活，在不平衡系统中更具优势[1]，并在有源电力滤波器[1，2]以及分布式并网发电[3，4]等场合得到了广泛应用。

四桥臂逆变器常用调制方法包括三维空间矢量脉宽调制(Three Dimensional Space Vector Pulse Width Modulation，3D-SVPWM)和载波脉宽调制(Carrier Base Pulse Width Modulation，CBPWM)等。3D-SVPWM调制算法以其输出谐波畸变率小、易于数字化实现以及直流侧电压利用率高等优势在四桥臂逆变器中被广泛采用[5]。在3D-SVPWM基础上提出的简化算法直接利用三相参考电压矢量计算开关器件导通时刻[6]，较传统算法计算量减小，更加简单直观。

为避免同一桥臂的上下开关管同时导通，需要在3D-SVPWM调制过程中加入死区时间。死区时间的加入会降低输出电压对参考电压的等效程度，尤其在有源滤波器等对开关频率要求较高的应用场合中，逆变器受死区的影响会更大，所以对逆变器的死区效应补偿非常有必要。众多学者针对死区补偿进行了研究，所提出的方法可分为平均电压补偿法和脉冲调整补偿法两类。文献[7-10]将死区效应看作扰动电压，通过在参考电压上叠加补偿电压以抵消扰动引起的平均误差电压，从而实现死区补偿，这种方法易于实现，但补偿准确度不高。文献[11-16]提出基于脉冲调整的补偿方法，在不改变脉冲作用等效程度的情况下，通过改变单相触发脉冲，避免死区带来的不良影响，可对死区时间[11-13]、器件开关延时[14，15]、管压降[14，15]以及电路中寄生参数[16]带来的死区效应进行补偿，这种方法能够对死区效应进行较精确的补偿，但对控制器的要求更高。死区补偿通常依赖于电流极性判断，但电流过零时易引起极性误判，造成过零点附近无法完全补偿死区。文献[9，13]通过观测扰动电压矢量以避免直接检测电流方向，文献[10，15]对电流进行滤波以减小高频噪声和零电流钳位现象的影响。以上方法不同程度地解决了三桥臂逆变器的死区效应问题。

本文采用简化3D-SVPWM算法对四桥臂逆变器进行调制。针对四桥臂逆变器开关状态多、电压矢量分布复杂以及死区补偿实现困难的问题，通过分析死区对四桥臂逆变器基矢量作用时间的影响，归纳四桥臂逆变器各相电流极性与对应脉冲调整方案的关系，将基于脉冲调整的死区补偿策略应用于四桥臂逆变器。该策略根据四桥臂输出电流极性特点，对一相或两相桥臂的驱动信号实施调整，并根据电流极性判断开关器件应提前或延迟触发，以达到校正基矢量作用时间的目的，抑制死区效应。最后对基于脉冲调整的四桥臂逆变器死区补偿策略进行了仿真和实验分析。

1　四桥臂逆变器结构及简化算法

四桥臂逆变器的拓扑结构如图1所示，逆变器包括a、b、c、f四个桥臂，va、vb、vc、vf分别为各相输出电压，ia、ib、ic、if分别为各相输出电流，Vdc为直流侧电压。

图1　四桥臂逆变器拓扑结构Fig.1　Four-leg inverter topology

四桥臂逆变器中任一桥臂上管导通以p表示，下管导通以n表示，共16种开关状态，对应矢量在αβγ坐标系中的分布如图2所示。16个基矢量构成一个六棱柱，该六棱柱由6个三棱柱组成，每个三棱柱由4个四面体组成，共24个四面体。3D-SVPWM策略利用2个零矢量和3个非零矢量合成参考电压矢量[5]。

图2　基矢量在α β γ坐标系中的分布Fig.2　Base vectors in α β γ coordinate

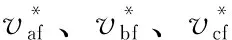
图3　简化3D-SVPWM算法流程图Fig.3　Flow chart of simplified 3D-SVPWM

2　死区效应分析

以四桥臂逆变器的一相桥臂为例分析死区时间对逆变器的影响，如图4所示，其中v为输出电压，i为输出电流。

图4　单相桥臂Fig.4　Single leg

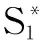
(1)

Te=Td+ton-toff

(2)

由图5可知，四桥臂逆变器调制过程中加入的死区时间会导致实际电压偏离参考值，降低实际输出电压与参考电压的等效程度，其偏差受电流极性影响。

图5　单相桥臂触发脉冲及输出电压Fig.5　Trigger pulse and output voltage of single leg

3　四桥臂逆变器死区补偿策略

将电压基矢量投影到αβ坐标系中，根据文献[17]，逆变器带阻性负载时，电流极性与基矢量投影之间的关系如图6所示，其中正负号由内至外分别表示a、b、c及第四桥臂的输出电流极性，“+”表示电流从桥臂流出，“-”表示电流流入桥臂，“x”表示电流极性可为正或负，扇区Ⅰ～Ⅵ对应图2所示α β γ坐标系中6个三棱柱在αβ平面中的投影。

图6　电流极性与基矢量投影的关系Fig.6　Relationship between current and voltage projection

若a、b、c三相电流极性为“+--”，则电流矢量在区域1或12内。

以电流矢量在区域1内为例：当逆变器所带负载为阻性时，电压矢量处在三棱柱Ⅰ内；当负载为阻感性时，由于电流矢量滞后电压矢量，可判断电压矢量位于三棱柱Ⅰ或三棱柱Ⅱ内，如图7所示。

以下讨论电压矢量位于三棱柱Ⅰ内的四面体T1中时所需的脉冲调整方案。

如果中线电流极性为“+”，则四面体T1对应电压基矢量的作用时间及其理想驱动信号如图8中虚线所示，根据图5可知，加入死区后，等效驱动信号如图8中实线所示。

图8　中线电流为“+”时T1中基矢量的作用时间Fig.8　Duty factors of T1 vectors when neutral current is “+”

由图8可见，加入死区时间后，V1、V3的作用时间不受影响，V2的作用时间缩短了2Te。为抑制死区效应，应补偿V2基矢量的作用时间，以保证输出电压等效程度。具体调整方案为：不改变b、c两相驱动信号，提前触发a相与第四桥臂上开关管，触发时刻调整如式(3)所示。

(3)

如果中线电流极性为“-”，加入死区时间后，V2、V3的作用时间不受影响，V1的作用时间缩短了2Te，如图9所示。为保证输出电压等效程度，相应调整方案为：不改变b、c两相驱动信号，提前触发a相与第四桥臂上开关管，触发时刻调整如式(4)所示。

(4)

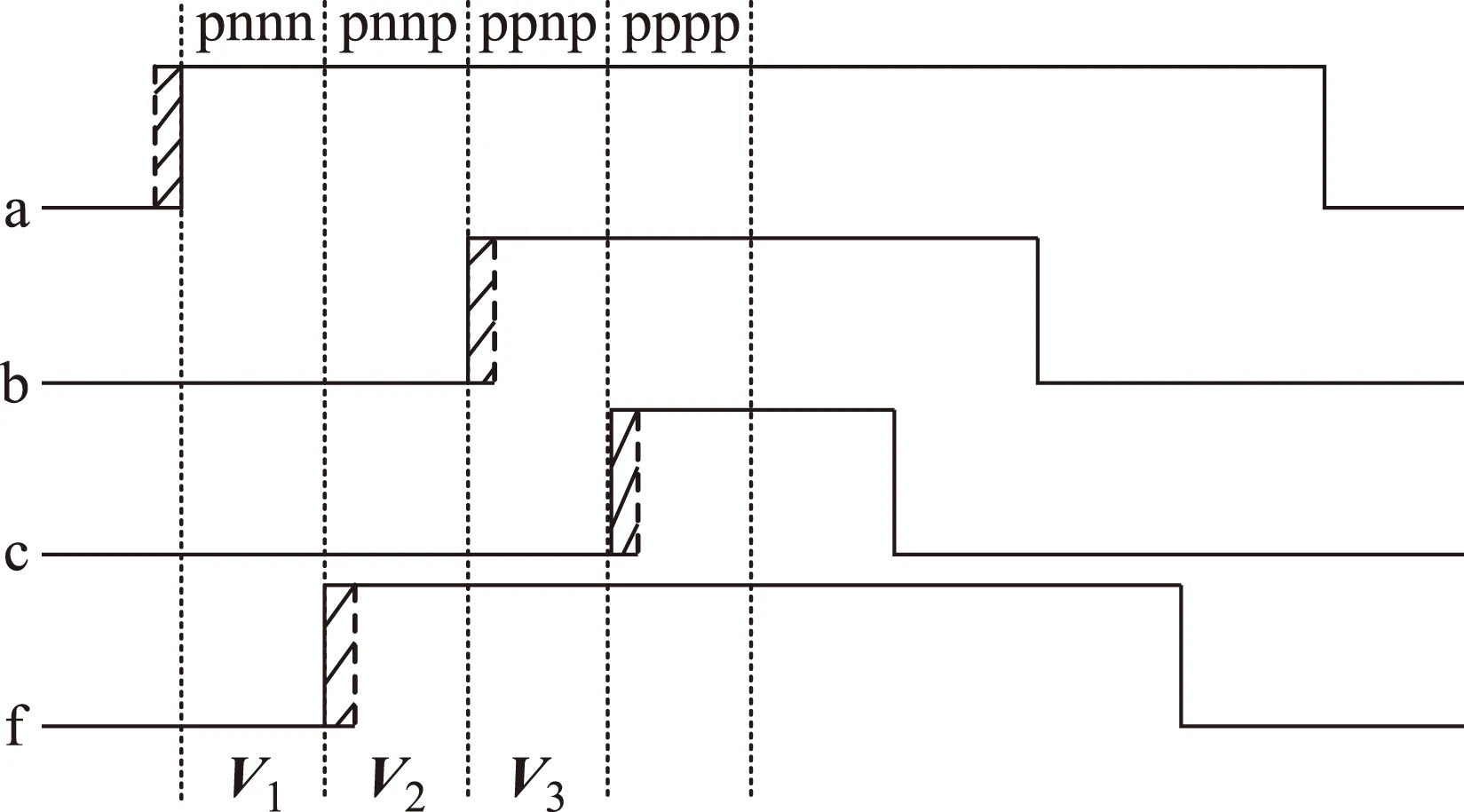
图9　中线电流为“-”时T1中基矢量的作用时间Fig.9　Duty factors of T1 vectors when neutral current is “-”

根据以上分析方法可得，当电压矢量处于四面体T2、T13、T14、三棱柱Ⅱ内或电流矢量处于图6中的区域12内时，所需脉冲调整方案均相同，可根据中线电流极性对a相和第四桥臂上开关管的触发时刻进行调整：中线电流极性为“+”时触发时刻调整如式(3)所示；中线电流极性为“-”时触发时刻调整如式(4)所示。

分析表1可总结出如下规则：

1)若一相电流极性异于其余三相，则对极性相异相的上桥臂触发时刻进行调整。极性相异相的电流极性为“+”时，该相触发时刻应提前Te；极性为“-”时，该相触发时刻应延迟Te。

2)若两相电流极性异于其余两相，则对中线和与中线同极性相的上桥臂触发时刻进行调整。中线和与中线同极性相的电流极性为“+”时，这两相的触发时刻应提前Te；电流极性为“-”时，相应触发时刻应延迟Te。

表1　脉冲调整后各桥臂上开关管的触发时刻Tab.1　Triggering time of ever leg’s upper switch after tuning pulse

以上规则表明在同一电流极性下脉冲调整方案具有一致性，只需判断电流极性即可确定四桥臂逆变器死区补偿脉冲调整方案，得到待调整驱动信号及其触发调整方式。此规则简化了死区补偿算法，使四桥臂逆变器的死区补偿易于实现。

4　仿真与实验分析

为验证基于脉冲调整的四桥臂逆变器死区补偿策略的有效性，下文进行了仿真和实验分析。

采用Maltab/Simulink仿真软件对基于脉冲调整的四桥臂逆变器死区补偿策略进行仿真分析，主电路为两电平四桥臂结构，带星形联结的阻感负载，三相参考电压如式(5)所示，系统参数如表2所示。

(5)

忽略器件的开通与关断延时，为了便于比较调制电压与参考电压的等效程度，利用截止频率为500 Hz的低通滤波器滤除输出相电压的高频成分，以得到交流侧等效电压波形。无死区时和死区补偿前后的a相电压频谱如图10所示，死区补偿前后a相电流波形与频谱如图11所示。

表2　仿真和实验时系统的主要参数Tab.2　Simulation and experiment’s parameters

图10　逆变器输出a相电压频谱Fig.10　Output voltage THD of phase a

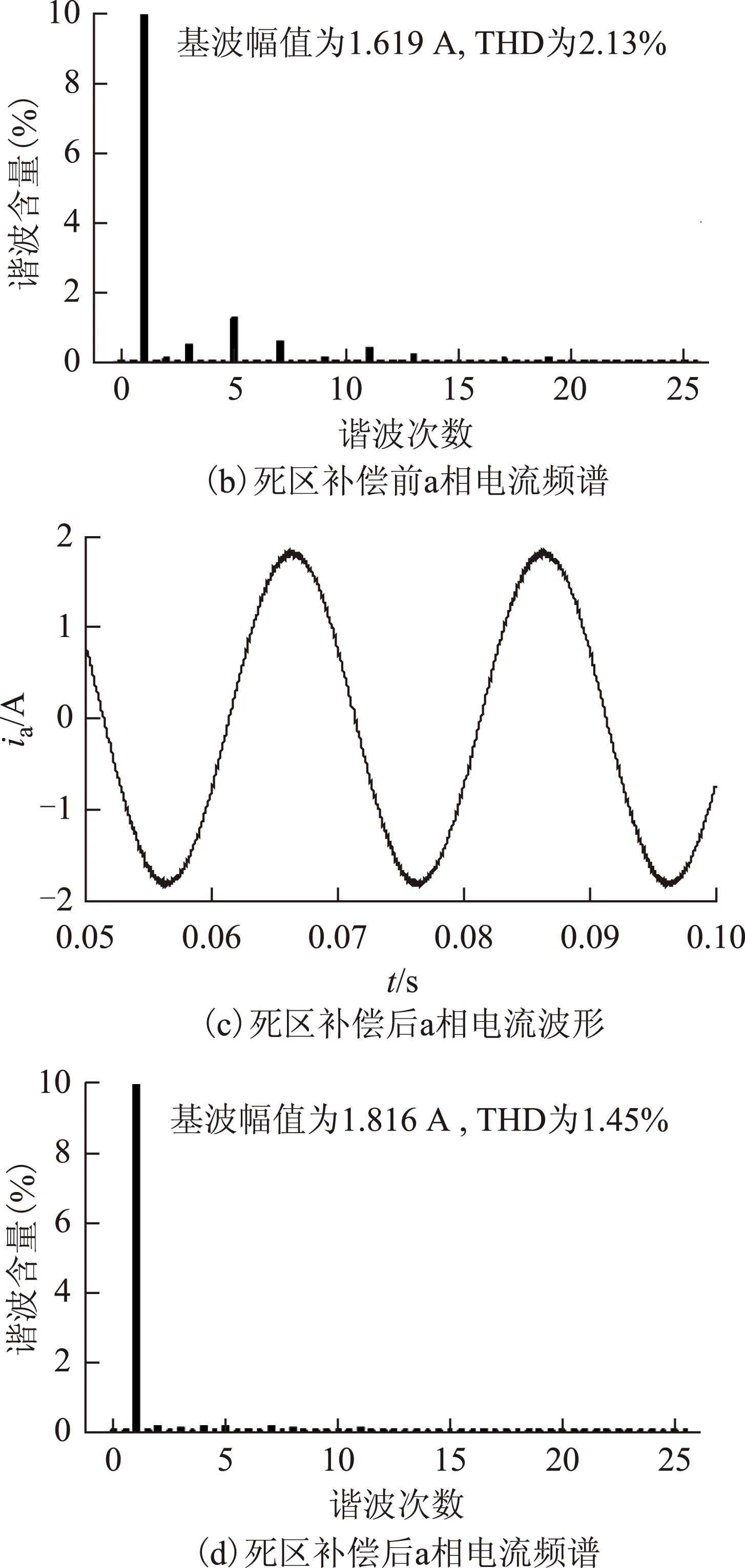
图11　逆变器输出a相电流波形与频谱Fig.11　Output current wave and THD of phase a

由图10和图11可知，加入死区时间后：逆变器输出能力下降，基波电压幅值由10 V降低到8.9 V，基波电流幅值为1.62 A；谐波畸变率上升，电压畸变率由1.11%上升为4.14%，电流畸变率为2.13%，其中部分奇次谐波由死区效应导致。采用脉冲调整法对该四桥臂逆变器死区补偿后：逆变器输出能力提高，基波电压幅值上升为参考值10 V，基波电流幅值上升为1.82 A；波形畸变程度减小，电压畸变率降低到1.37%，电流畸变率降低到1.45%。

同一电流极性下，电压矢量所在位置不同，为了验证不同功率因数下所给出的脉冲调整方案的正确性，调整表2中电感参数，使功率因数如表3中所示，其他参数不变，通过仿真，死区补偿前后a相电压幅值与畸变率如表3所示。

由表3可知，基于脉冲调整的四桥臂逆变器死区补偿策略在不同负载功率因数下均能较好地补偿死区

效应，提高桥臂输出能力，抑制死区造成的波形畸变。

表3　不同功率因数时的死区补偿效果Tab.3　Compensation effects in different power factors

若系统三相不平衡，设三相参考电压如式(6)所示，a相参考电压含5次谐波成分，5次谐波含量为20%，系统参数如表2所示。死区补偿前后三相电压波形与a相电压频谱如图12所示，a相电流波形与频谱如图13所示。

(6)

对比图12和图13可知，死区补偿后输出电压基波幅值更接近参考值10 V，a相基波电流幅值由1.63 A上升为1.83 A；补偿后波形等效程度升高，a相电压5次谐波含量由18.08%上升为19.26%，更接近参考值20%，输出电压中3次、7次谐波含量分别由1.91%、1.65%下降为0.29%、0.91%，输出电流中3次、7次谐波含量分别由0.54%、0.58%下降为0.16%、0.15%。

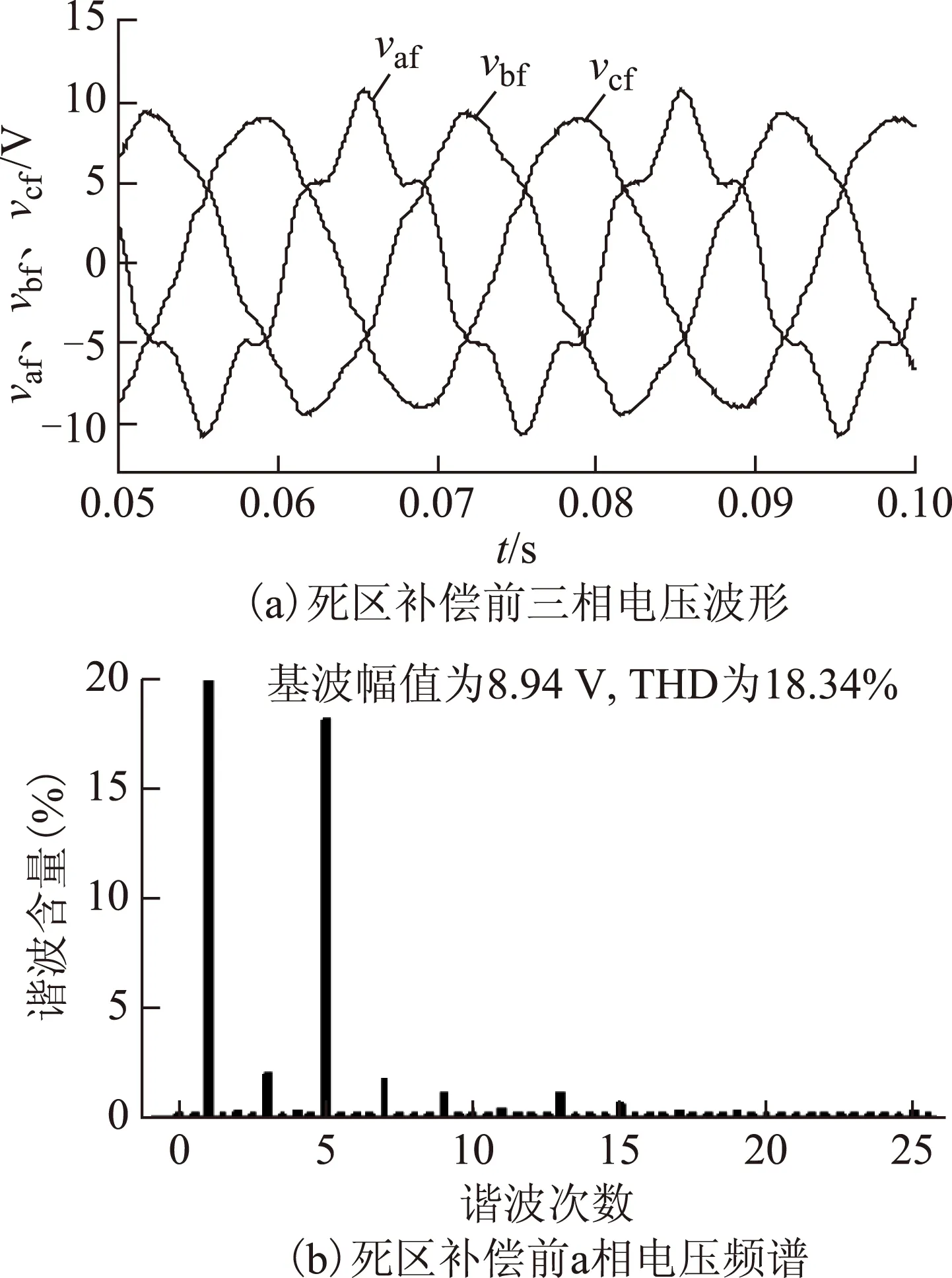
图12　三相不平衡时的电压波形与频谱Fig.12　Voltage wave and THD when loads are unbalanced

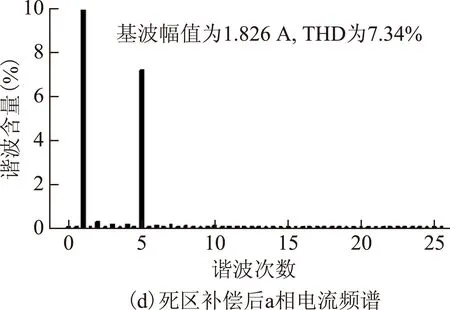
图13　叠加5次谐波后a相电流波形与频谱Fig.13　Current wave and THD of phase a when 5th harmonic is added

基于四桥臂变流器平台对该脉冲调整策略进行实验验证，开关器件采用BSM50GB120DLC型IGBT模块，控制器采用德州仪器公司的TMS320F2812型数字信号处理器，利用FLUKE435电能质量分析仪对a相输出电流进行谐波分析。实验参数与仿真参数一致，如式(5)和表2所示。死区补偿前后a相电流波形和频谱如图14所示。

图14　逆变器输出电流a相波形与频谱Fig.14　Output current wave and THD of phase a

由图14可见，死区补偿后逆变器输出能力提高，输出电流有效值由1.08 A上升为1.22 A；输出电流波形畸变程度减小，畸变率由2.1%降低到1.4%，与仿真效果一致。

对三相不平衡工况下四桥臂逆变器死区补偿策略的可行性进行实验验证，参考电压如式(6)所示，系统参数如表2所示。死区补偿前后a相电流波形与频谱如图15所示。

图15　叠加5次谐波后a相电流波形与频谱Fig.15　Current wave and THD of phase a when 5th harmonic is added

由图15可见，死区补偿后逆变器输出能力及波形等效程度均得到了提升，3次、7次电流谐波含量分别由1.3%、0.7%下降到0.7%、0.3%，与仿真效果一致。

以上仿真和实验结果表明，基于脉冲调整的四桥臂逆变器死区补偿策略在三相平衡及不平衡情况下均能提高四桥臂逆变器输出能力，抑制死区造成的波形畸变，提高输出波形对参考波形的等效程度，有效抑制了死区效应带来的不良效果，验证了基于脉冲调整的四桥臂逆变器死区补偿策略的可行性和有效性。

5　结论

本文分析了死区对四桥臂逆变器性能的影响，死区的加入导致逆变器输出能力下降、波形等效程度降低。针对四桥臂逆变器死区补偿实现困难的问题，将基于脉冲调整的死区补偿策略应用于四桥臂逆变器，该方法仅需判断电流极性即可确定待调整的驱动信号及其触发调整方式，在同一电流极性下脉冲调整具有一致性，易于实现。仿真结果表明在不同负载功率因数下该四桥臂变流器死区补偿策略均能有效补偿死区效应；仿真和实验结果表明所给出的方案在三相平衡及三相不平衡工况下均能提高逆变器输出能力、减小死区造成的波形畸变程度，验证了应用于四桥臂变流器的死区补偿方案的有效性和可行性。

[1]刘海波，毛承雄，陆继明，等.四桥臂三相四线制并联型APF-STATCOM[J].电力系统保护与控制，2010，38(16)：11-17.

Liu Haibo，Mao Chengxiong，Lu Jiming，et al.Three-phase four-wire shunt APF-STATCOM using a four-leg converter[J].Power System Protection and Control，2010，38(16)：11-17.

[2]张晓，李新宇，周睿.三相四桥臂并联型APF无差拍控制策略的研究[J].电力系统保护与控制，2011，39(20)：78-83.

Zhang Xiao，Li Xinyu，Zhou Rui.Study on a deadbeat control scheme for three-phase four-leg shunt active power filter[J].Power System Protection and Control，2011，39(20)：78-83.

[3]耿乙文，伍小杰，周德佳，等.基于改进型比例谐振控制器的三相四线制光伏发电和有源滤波器系统[J].电工技术学报，2013，28(8)：142-148.

Geng Yiwen，Wu Xiaojie，Zhou Dejia，et al.Research on three phase four wire PV-AF system based on improved proportional resonant controllers[J].Transactions of China Electrotechnical Society，2013，28(8)：142-148.

[4]周啸，金新民，唐芬，等.三相四桥臂微网变流器在离网不平衡负载下的控制策略及其实现[J].电力系统保护与控制，2013，41(19)：24-31.

Zhou Xiao，Jin Xinmin，Tang Fen，et al.Islanded-mode control and implementation of a three-phase four-leg based microgrid converter under unbalanced load conditions[J].Power System Protection and Control，2013，41(19)：24-31.

[5]周娟.四桥臂有源电力滤波器关键技术研究[D].徐州：中国矿业大学，2011.

[6]周娟，刘马隆，王晓莹，等.四桥臂变流器简化空间矢量调制策略[J].电力电子技术，2015，49(1)：1-5.

Zhou Juan，Liu Malong，Wang Xiaoying，et al.A simplified space vector pulse width modulation algorithm for four-leg converter[J].Power Electronics，2015，49(1)：1-5.

[7]Hwang Seon-Hwan，Kim Jang-Mok.Dead time compensation method for voltage-fed PWM inverter[J].IEEE Transactions on Energy Conversion，2010，25(1)：1-10.

[8]Kim Sam-Young，Lee Wootaik，Rho Min-Sik，et al.Effective dead-time compensation using a simple vectorial disturbance estimator in PMSM drives[J].IEEE Transactions on Industrial Electronics，2010，57(5)：1609-1614.

[9]何正义，季学武，瞿文龙.一种新颖的基于死区时间在线调整的SVPWM补偿算法[J].电工技术学报，2009，24(6)：42-47.

He Zhengyi，Ji Xuewu，Qu Wenlong.A novel SVPWM compensation strategy based on regulating dead time on-line[J].Transactions of China Electrotechnical Society，2009，24(6)：42-47.

[10]杨荣峰，陈伟，于泳，等.自适应滤波在电流矢量死区补偿方法中的应用[J].电工技术学报，2009，24(7)：65-69.

Yang Rongfeng，Chen Wei，Yu Yong，et al.Adaptive filter application in current vector dead time compensation[J].Transactions of China Electrotechnical Society，2009，24(7)：65-69.

[11]杨燕波，吴庆彪.逆变器脉宽调制中基于脉冲的死区补偿方法[J].电力电子技术，2009，43(3)：70-72.

Yang Yanbo，Wu Qingbiao.The dead-time compensator method for PWM voltage inverters based on the pulse[J].Power Electronics，2009，43(3)：70-72.

[12]Patel P J，Patel V，Tekwani P N.Pulse-based dead-time compensation method for selfbalancing space vector pulse width-modulated scheme used in a three-level inverter-fed induction motor drive[J].IET Power Electronics，2011，4(6)：624-631.

[13]周华伟，温旭辉，赵峰，等.一种新颖的电压源逆变器自适应死区补偿策略[J].中国电机工程学报，2011，31(24)：26-32.

Zhou Huawei，Wen Xuhui，Zhao Feng，et al.A novel adaptive dead-time compensation strategy for VSI[J].Proceedings of the CSEE，2011，31(24)：26-32.

[14]周京华，贾斌，章小卫，等.三电平逆变器死区补偿策略研究[J].电机与控制学报，2013，17(5)：69-74.Zhou Jinghua，Jia Bin，Zhang Xiaowei，et al.Research on dead-time compensation strategy of three-level inverter[J].Electric Machines and Control，2013，17(5)：69-74.

[15]张辑，彭彦卿，陈天翔.一种基于电流空间矢量的新型死区补偿策略[J].电工技术学报，2013，28(6)：127-132.Zhang Ji，Peng Yanqing，Chen Tianxiang.A novel dead time compensation strategy based on current space vector[J].Transactions of China Electrotechnical Society，2013，28(6)：127-132.

[16]Zhang Zhendong，Xu Longya.Dead-time compensation of inverters considering snubber and parasitic capacitance[J].IEEE Transactions on Power Electronics，2014，29(6)：3179-3187.

[17]胡庆波，吕征宇.一种新颖的基于空间矢量PWM的死区补偿方法[J].中国电机工程学报，2005，25(3)：13-17.

Hu Qingbo，Lü Zhengyu.A novel method for dead-time compensation based on SVPWM[J].Proceedings of the CSEE，2005，25(3)：13-17.

Dead-time Compensation Strategy for Four-leg Inverter Based on Pulse-tuning

Zhou Juan1Chen Ying1，2Tang Huiying1Wei Chen1Wu Xuan1

(1.School of Information and Electrical EngineeringChina University of Mining and Technology Xuzhou221008China 2.Sichuan Electric Power Design & Consulting Co.LtdChengdu610041China)

To avoid the short circuit of the bridge，the dead-time is often added，which causes the drop of the output capability and the distortion of the output waveforms，and needs to be compensated.The dead-time compensation of the four-leg inverter is hard to be implemented due to its multiple switch states and complex voltage vectors distribution.The forming mechanism of the dead-time effect is firstly analyzed.Then the relevance between the currents polarities and the corresponding compensation methods are generalized.Afterwards a dead-time compensation strategy based on pulse-tuning for four-leg inverters is obtained.This compensation strategy has consistency in specific currents polarities.So it is easy to be implemented.The compensation method is determined as long as the currents polarities are distinguished.The dead-time effect is compensated by correcting the duty factors of the base vectors.Simulation and experiment results prove that the proposed compensation strategy is effective in both balanced and unbalanced situation，can raise the output capability，and reduce the waveform distortion.

Four-leg inverter，3D-SVPWM，dead-time compensation，pulse-tuning

2015-01-27改稿日期2015-11-30

TM464

周娟女，1976年生，博士，教授，研究方向为电能质量控制、电力电子技术与应用。

E-mail：zhjcumt@126.com(通信作者)

陈映男，1991年生，硕士研究生，研究方向为电能质量控制技术。

E-mail：903495603@qq.com

国家自然科学基金资助项目(51407184)。