两逆变器并联IPT系统的环流消除方法研究

麦瑞坤　陆立文　李　勇

(磁浮技术与磁浮列车教育部重点实验室　成都　610031)



两逆变器并联IPT系统的环流消除方法研究

麦瑞坤陆立文李勇

(磁浮技术与磁浮列车教育部重点实验室成都610031)

采用一种基于相量调节的环流消除方法，用以解决高频逆变器并联时产生的环流问题。首先详细分析了LCCL型两逆变器并联感应电能传输(IPT)系统的拓扑结构以及环流产生的原因；其次，以一次绕组电流为参考，计算出支路的虚拟有功无功分量，并分析其与相量调节控制目标的对应关系，给出环流消除的控制策略；最后，以两个并联高频逆变器的IPT系统进行实验验证，实验结果表明，此IPT系统的直流电源最大输出总功率约为1.4 kW，系统整体效率(DC-DC)可达89.82%，且两个高频逆变器之间的环流得以有效控制，证明了该方法的有效性。

高频逆变器并联技术感应电能传输相量调节环流消除虚拟有功无功

0　引言

感应电能传输(Inductive Power Transfer，IPT)系统通常采用高频电力电子变换技术，将电能转换为磁能，再将磁能转换为电能，实现能量的无线传输[1-4]。应用IPT技术为轨道交通列车及电动汽车等移动设备供电，克服了传统的有线电能传输技术易积碳、产生接触火花以及插接操作繁琐等缺陷，有效提高了供电的品质、安全性和可靠性，具有较高的研究价值[5-9]。

应用IPT技术为轨道交通列车及电动汽车等大功率公共交通设备供电时，由于受到功率开关器件MOSFET和IGBT容量与成本限制，单个高频逆变器往往较难满足IPT系统大功率电能传输的需求[10-13]。目前主要采用多电平或并联技术来提高IPT系统中高频逆变器的整体容量。文献[14]将级联型多电平逆变器技术应用到大功率IPT系统，采用阶梯波移相合成的方法，在消除级联型多电平逆变器输出电压三次以及三次奇数倍谐波的同时，提高了IPT系统的整体容量，并阐明了功率调节的具体方法，但未详细说明闭环的控制过程。文献[15]将高频逆变器并联技术应用到大功率IPT系统，通过灵活配置逆变器的数量，来满足用电设备的功率等级需求，降低了IPT系统的设计周期以及开发成本，并提高了IPT系统的可靠性，但未具体分析各高频逆变器之间环流产生的原因以及环流消除的方法。

多个高频逆变器并联时，由于电子元器件的容差、连接电感电容值的差异以及输入直流电压的不同等因素，使得并联的高频逆变器之间存在差异[16]，从而导致环流的产生；该环流的存在会增加流过功率开关器件的电流，影响逆变器支路之间的功率均分，降低系统的整体性能。为了消除环流的影响，需要对多个逆变器并联的IPT系统进行环流消除控制，使得各高频逆变器支路的电流幅值和相位都相等，同时为了保证IPT系统运行安全以及功率输出的稳定，多采用恒定一次绕组电流的控制方案[17]。文献[16]提出了基于相量调节的环流消除方法，该方法能有效减小各并联高频逆变器支路电流的幅值误差和相位误差，并能有效保证总线电压的恒定，而IPT系统一般要求恒定一次绕组电流，且为了保证各高频逆变器支路输出电压电流的正弦度，各并联单元中加入了串联谐振和并联谐振电路，电感电容数量较多，成本较高。但该方法只是针对纯阻性负载情况进行了分析。文献[18]提出一种直接功率控制方案，可实现瞬时有功和无功功率计算，提高了瞬时功率计算准确度，但该方案只对工频情况下单个模块瞬时功率计算和控制进行了阐述，并未涉及到多个模块在高频情况下瞬时功率的计算。

本文采用一种基于两逆变器并联IPT系统的相量调节的环流消除方法，首先理论分析了两个LCCL型IPT系统中环流产生的原因，其次详细阐述了虚拟有功无功的计算过程，然后具体描述了环流消除的控制策略，最后以两个并联高频逆变器的IPT系统为实验对象，对比分析了加入环流消除控制算法前后的性能，实验结果表明，加入环流消除环节后，各支路之间的环流显著减小，达到了恒流控制与环流消除的目的。

1　IPT系统的参数设计及环流分析

1.1LCCL型单逆变器的IPT系统分析

LCCL型单逆变器的IPT系统拓扑如图1所示。图中，高频逆变器输入直流电压幅值为E；Q1～Q4为功率MOSFET器件，VD1～VD4为器件体二极管；高频逆变器的输出电压为u，输出电流为i；L、C构成谐振电路，且谐振频率为系统的工作频率ω；LP为一次绕组的等效电感；CP为一次绕组的谐振补偿电容；L、C、CP、LP构成LCCL谐振补偿拓扑；M为一、二次绕组的互感；LS为二次绕组的等效电感；CS为二次绕组谐振补偿电容；VDr1～VDr4为全桥整流二极管；Cr为负载电阻两端并联的滤波电容；RL为负载电阻。由图1中电流iP方向看过去的等效负载部分可等效为阻感性负载Ze=Re+jωLe，电容CS完全补偿二次绕组的等效电感LS时[19，20]

(1)

配置一次侧谐振补偿电容CP的值为

(2)

使得等效负载感性部分的电感值Le与电感L的值相等，构成LCLe谐振补偿，实现全桥逆变器的输出电压u与电流i同相，即软开关[21]。

图1　LCCL型单逆变器的IPT系统Fig.1　The IPT system with a LCCL-based single inverter

1.2两逆变器并联IPT系统参数设计及环流分析

LCCL型两逆变器并联的IPT系统如图2所示，等效负载部分等效为Re和Le；L1、C1构成逆变器一的谐振电路；L2、C2构成逆变器二的谐振电路；E1、E2分别为两逆变器输入的直流电压；u1、u2分别为两逆变器输出电压；i1、i2分别为两逆变器输出电流；i1P、i2P分别为两逆变器支路电流；LCCL型两逆变器并联的IPT系统的谐振补偿拓扑可用LCCL型单逆变器的IPT系统谐振补偿拓扑等效[22]，则电感电容值的设计规则为

(3)

图2　LCCL型两逆变器并联的IPT系统Fig.2　The IPT system with LCCL-based two parallel-connected inverters

LCCL型两逆变器并联的IPT系统等效电路如图3所示，忽略电感电容的电阻值；逆变器输出电压u1和u2分别经过L1C1和L2C2谐振电路滤波后，可用基波电压u1.1和u2.1等效表示逆变器输出电压；由式(3)即可求得L1、L2、Le和CP的值。

图3　LCCL型两逆变器并联的IPT系统等效电路Fig.3　The IPT equivalent circuit with LCCL-based dual parallel-connected inverters

再根据基尔霍夫电压电流定律，得到电路方程为

(4)

由式(4)可求得各逆变器支路电流为

I1P=

(5)

I2P=

(6)

以高频逆变器一的输出基波电压U1.1、谐振电感L1以及谐振电容C1为参考，由式(3)可得L1、C1谐振时ZL1+ZC1=0；假设逆变器二的输出基波电压U2.1、谐振电感L2以及谐振电容C2与逆变器一存在如下关系：ZL 2=kZLZL1，ZC 2=kZCZC1，U2.1=kuU1.1。实际中，开关器件、电感电容和直流电源之间存在一定的容差，可能导致谐振网络不谐振以及逆变器输出基波电压不相等的情况，具体可分为以下3种情况：

1)直流电源电压不相等：kZL=1、kZC=1、ku≠1，环流可表示为

(7)

2)谐振电感阻抗不相等：kZL≠1、kZC=1、ku=1，环流可表示为

(8)

3)谐振电容阻抗不相等：kZL=1、kZC≠1、ku=1，环流可表示为

(9)

由式(7)～式(9)可知，逆变器一和逆变器二的谐振电感、谐振电容或逆变器输入电压不相等都会引起两个逆变器支路之间的环流不为零。

(10)

由图4易看出，两个逆变器并联的IPT系统中，各支路输出电流矢量不相等时逆变器之间存在环流。

图4　相量调节消除环流的控制示意图Fig.4　The phasor control schematic diagram of eliminating the circulating current

2　逆变器支路虚拟有功和无功功率计算

为了保证IPT系统运行安全以及功率输出的稳定，多采用一次绕组恒流的控制方案[17]，本节以一次绕组电流值作为参考，对两个逆变器支路虚拟有功和无功功率的求解进行详细阐述。如图2所示，LCCL型两逆变器并联的IPT系统，以一次绕组电流iP为参考，则iP的相角为零，如图4所示。iP为正弦波，频率为系统工作频率ω，幅值为IPm，则

iP=IPmsin(ωt)

(11)

各逆变器支路电流为正弦波ikP，幅值为IkPm，相角为φk，其中k=1，2，则

ikP=IkPmsin(ωt+φk)=ikPasin(ωt)+ikPrcos(ωt)

(12)

式中

(13)

各逆变器虚拟有功功率和无功功率定义为

(14)

控制器对一次绕组电流iP锁相后给出与系统工作频率ω相同的参考信号为

(15)

式中，φr为相对于一次绕组电流iP的初始相位差。

将各逆变器支路电流ikP和一次绕组电流iP分别乘以式(15)中的参考信号，简化可得

(16)

(17)

由式(16)和式(17)可得，ikPsin、ikPcos、iPsin和iPcos中分别含有二倍系统工作频率的分量和直流分量，将式(16)和式(17)经过低通滤波后，可得直流分量为

(18)

由式(18)得到一次绕组电流iP的幅值为

(19)

由式(14)和式(18)可得各逆变器支路虚拟有功和无功功率为

(20)

3　基于相量调节的环流消除方法

3.1相量调节与虚拟有功和无功功率的关系分析

由式(5)和式(6)可得，系统中的器件选定时，各阻抗值就确定，各逆变器支路电流只与逆变器输出基波电压相关；通过控制逆变器输出电压脉宽和移相角来改变逆变器输出基波电压的幅值和移相角，进而可控制逆变器支路电流ikP的幅值IkPm和相角φk，其中k=1，2。如图4所示，两个高频逆变器并联的IPT系统中，逆变器的支路电流i1P和i2P、幅值和相角都不相等。为了减小逆变器的环流Δi，需要对各高频逆变器支路电流进行幅值和相角双环控制，使得两个逆变器的支路电流相等，且满足与一次绕组电流iP的关系为i1P=i2P=iP/2，即幅值和相角都相等：I1Pm=I2Pm=IPm/2，φ1=φ2=0；进而得到各逆变器支路电流的控制目标为

(21)

将式(21)代入到式(14)，得到虚拟有功和无功功率的控制目标为

(22)

3.2环流消除的控制方法

由式(22)和图4可看出，通过反馈各逆变器支路虚拟有功和无功功率的大小，再加以相量控制，最终可达到减小环流Δi和恒定一次绕组电流幅值IPm的目的，具体控制过程如图5所示。

图5　基于相量调节环流消除的控制框图Fig.5　The phasor control strategy schematic of eliminating the circulating current

图5中，Ka(s)为虚拟有功均分控制器，Kr(s)为虚拟无功最小化控制器，Ki(s)为一次绕组电流控制器，IPm_ref为一次绕组电流幅值设定值，(P1+P2)/2为虚拟有功参考值，虚拟无功参考值为零。输入任意一个逆变器的支路电流ikP和一次绕组电流iP到控制器后，求解出虚拟有功Pk、无功Qk以及一次绕组幅值IPm，k=1，2；Ka(s)、 Kr(s)和Ki(s)均为PI控制器模块，控制器模块输出脉宽值和移相角传送给脉冲产生器，脉冲产生器产生逆变器的控制脉冲，控制脉冲控制第k个逆变器输出电压为uk，再经过LkCk谐振电路，得到反馈电流ikP；最终，控制器可控制输出一次绕组电流为设定电流值IPm_ref，各逆变器的支路电流ikP相等，环流Δi为零。

4　实验验证

为验证以上分析的正确性，本节采用表1所示的系统参数，按照图2搭建了LCCL型两逆变器并联IPT系统，为了改善支路电流波形的质量，在逆变器一电流支路串联一个LfCf串联谐振滤波电路，且谐振频率为ω，实验装置如图6所示。控制系统以TMS320F28335作为控制核心，功率开关器件为IRF640N。式(16)和式(17)经过的低通滤波器为巴特沃斯(Butterworth)二阶滤波器，滤波器的采样频率为160 kHz，截止频率为100 Hz。本次实验过程中，使用功率分析仪测量IPT系统的直流电源最大输出总功率约为1.4 kW，每个逆变器输入功率约为700 W，整个系统的效率达到89.82%，其中功率分析仪型号为Hioki 3390。

表1　IPT系统参数Tab.1　The configuration of the IPT system

图6　实验装置图Fig.6　The experimentation setting

由1.2节对环流的分析可得，输入高频逆变器的直流电压E不相等，谐振电感L1和L2不相等，或谐振电容C1和C2不相等，均会导致各高频逆变器的支路电流不相等。图7为输入直流电压E相等(E1=E2=80 V)、谐振电容C1和C2相等、谐振电感L1和L2不相等(L2=0.94L1)时，一次绕组电流iP幅值设定为IPm=12 A，高频逆变器的支路电流i1P、i2P和环流Δi的实验结果。可看出电流i1P和i2P的幅值和相角都不相等，环流Δi较大，其中两倍环流的峰峰值约为2.5 A。

图7　E1=E2、C2=C1、L2=0.94L1时， i1P、i2P和环流Δi实验波形Fig.7　The waveform of i1P,i2P and the circulating current Δi when E1=E2，C2=C1，L2=0.94L1

图8为输入直流电压E不相等(E1=0.94E2=80 V)、谐振电感L1和L2相等(L2=L1=130.5 μH)、谐振电容C1和C2相等时，一次绕组电流iP幅值IPm=12 A，高频逆变器的支路电流i1P和i2P及环流Δi的实验结果。可看出电流i1P和i2P的幅值和相角都不相等，环流Δi较大，其中两倍环流的峰峰值约为2 A。

图8　E1=0.94E2、C2=C1、L2=L1时， i1P、i2P和环流Δi实验波形Fig.8　The waveform of i1P,i2P and the circulating current Δi when E1=0.94E2，C2=C1，L2=L1

图9为输入直流电压E相等(E1=E2=80 V)、谐振电感L1和L2相等(L2=L1=130.5 μH)、谐振电容C1和C2不相等(C2=0.94C1=503.19 nF)时，一次绕组电流iP幅值IPm=12 A，高频逆变器的支路电流i1P和i2P及环流Δi的实验结果。可看出电流i1P和i2P的幅值和相角都不相等，环流Δi较大，其中两倍环流的峰峰值约为4 A。

图9　E1=E2、C2=0.94C1、L2=L1时， i1P、i2P和环流Δi实验波形Fig.9　The waveform of i1P,i2P and the circulating current Δi when E1=E2，C2=0.94C1，L2=L1

由图7～图9的实验结果可看出，LCCL型两逆变器并联的IPT系统，不加任何控制时，输入高频逆变器的直流电压E不相等，谐振电感L1和L2不相等，或谐振电容C1和C2不相等，都会导致逆变器支路电流i1P和i2P的幅值和相角不相等，环流Δi较大。采用上文分析的各逆变器支路虚拟有功无功的计算方法，计算出各逆变器支路虚拟有功和无功功率以及一次绕组电流幅值，再根据基于相量调节环流消除的控制方法(如图5所示)，即可达到各逆变器支路电流i1P和i2P的幅值和相角都相等，减小两个逆变器之间的环流Δi，均分各高频逆变器输出功率的目的。

由图10～图12的实验结果可看出，输入高频逆变器的直流电压E不相等，谐振电感L1和L2不相等，或谐振电容C1和C2不相等，在加入基于相量调节环流消除的控制方法后，两倍环流的峰峰值都小于1 A，控制器能有效减小两个逆变器之间的环流Δi；一次绕组电流幅值IPm等于设定电流幅值IPm_ref，IPm=IPm_ref=12 A；各逆变器支路电流i1P和i2P的幅值和相角都相等，且电流幅值I1Pm=I2Pm=6 A，相角φ1=φ2=0。

图10　E1=E2、C2=C1、L2=0.94L1时， 相量控制后i1P、i2P和环流Δi实验波形Fig.10　The waveform of i1P,i2P and the circulating current Δi with phasor control when E1=E2，C2=C1，L2=0.94L1

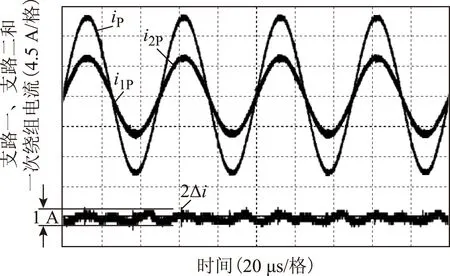
图11　E1=0.94E2，C2=C1，L2=L1时， 相量控制后i1P、i2P和环流Δi实验波形Fig.11　The waveform of i1P,i2P and the circulating current Δi with phasor control when E1=0.94E2，C2=C1，L2=L1

图12　E1=E2，C2=0.94C1，L2=L1时， 相量控制后i1P、i2P和环流Δi实验波形Fig.12　The waveform of i1P,i2P and the circulating current Δi with phasor control when E1=E2，C2=0.94C1，L2=L1

5　结论

在同等容量的开关器件下，本文采用高频逆变器并联的方式，相比于单个高频逆变器，提高了IPT系统的整体容量；为了消除并联高频逆变器时产生的环流，采用计算各并联逆变器支路虚拟有功和无功分量代替直接测量各并联逆变器支路电流幅值和相位的方法，提高了反馈量的准确度；最后，以两个并联高频逆变器的IPT系统进行实验验证，实验结果证明了该环流消除方法的有效性，各并联逆变器的支路电流和输出功率都相等，系统整体效率(DC-DC)可达89.82%。

致谢：感谢西南交通大学硕士研究生创新实验实践项目(YC201503105) 提供资金资助。

[1]孙跃，王智慧，戴欣，等.非接触电能传输系统的频率稳定性研究[J].电工技术学报，2005，20(11)：56-59.

Sun Yue，Wang Zhihui，Dai Xin，et al.Study of frequency stability of contactless power transmission system[J].Transactions of China Electrotechnical Society，2005，20(11)：56-59.

[2]苏玉刚，唐春森，孙跃，等.非接触供电系统多负载自适应技术[J].电工技术学报，2009，24(1)：153-157.

Su Yugang，Tang Chunsen，Sun Yue，et al.Load adaptive technology of contactless power transfer system[J].Transactions of China Electrotechnical Society，2009，24(1)：153-157.

[3]何正友，李勇，麦瑞坤，等.考虑阻感性负载IPT系统的动态补偿技术[J].西南交通大学学报，2014，49(4)：569-575.

He Zhengyou，Li Yong，Mai Ruikun，et al.Dynamic compensation strategy of inductive power transfer system with inductive-resistive load[J].Journal of Southwest Jiaotong University，2014，49(4)：569-575.

[4]李阳，杨庆新，闫卓，等.无线电能有效传输距离及其影响因素分析[J].电工技术学报，2013，28(1)：106-112.

Li Yang，Yang Qingxin，Yan Zhuo，et al.Analysis on effective range of wireless power transfer and its impact factors[J].Transactions of China Electrotechnical Society，2013，28(1)：106-112.

[5]赵争鸣，张艺明，陈凯楠.磁耦合谐振式无线电能传输技术新进展[J].中国电机工程学报，2014，33(3)：1-13.

Zhao Zhengming，Zhang Yiming，Chen Kainan.New progress of magnetically-coupled resonant wireless power transfer technology[J].Proceedings of the CSEE，2014，33(3)：1-13.

[6]范兴明，莫小勇，张鑫.磁耦合谐振无线电能传输的研究现状及应用[J].电工技术学报，2013，28(12)：75-82.

Fan Xingming，Mo Xiaoyong，Zhang Xin.Research status and application of wireless power transfer via coupled magnetic resonances[J].Transactions of China Electrotechnical Society，2013，28(12)：75-82.

[7]黄学良，谭林林，陈中，等.无线电能传输技术研究与应用综述[J].电工技术学报，2013，28(10)：1-11.

Huang Xueliang，Tan Linlin，Chen Zhong，et al.Review and research progress on wireless power transfer technology[J].Transactions of China Electrotechnical Society，2013，28(10)：1-11.

[8]麦瑞坤，陆立文，李勇，等.一种采用最小电压与最大电流跟踪的IPT系统动态调谐方法[J].电工技术学报，2015，30(19)：32-38.

Mai Ruikun，Lu Liwen，Li Yong，et al.Dynamic resonant compensation approach based on minimum voltage and maximum current tracking for IPT system[J].Transactions of China Electrotechnical Society，2015，30(19)：32-38.

[9]李勇，麦瑞坤，马林森，等.一种双初级线圈并绕的感应电能传输系统及其功率分配方法[J].中国电机工程学报，2014，35(17)：4454-4460.

Li Yong，Mai Ruikun，Ma Linsen，et al.Dual parallel wound primary coils based IPT systems and its power allocation technique[J].Proceedings of the CSEE，2014，35(17)：4454-4460.

[10]Chopra S，Bauer P.Driving range extension of EV with on-road contactless power transfer—a case study[J].IEEE Transactions on Industrial Electronics，2013，60(1)：329-338.

[11]Huh Jin，Lee Sungwoo，Park Changbyung，et al.high performance inductive power transfer system with narrow rail width for on-line electric vehicles[C]//2010 IEEE Energy Conversion Congress and Exposition，Atlanta，GA，2010：647-651.

[12]Covic G A，Boys J T.Modern trends in inductive power transfer for transportation applications[J].IEEE Journal of Emerging and Selected Topics in Power Electronics，2013，1(1)：28-41.

[13]张献，杨庆新，崔玉龙，等.大功率无线电能传输系统能量发射线圈设计、优化与验证[J].电工技术学报，2013，28(10)：12-18.

Zhang Xian，Yang Qingxin，Cui Yulong，et al.Design optimization and verification on the power transmitting coil in the high-power wireless power transmission system[J].Transactions of China Electrotechnical Society，2013，28(10)：12-18.

[14]李勇，麦瑞坤，陆立文，等.一种采用级联型多电平技术的IPT系统谐波消除与功率调节方法[J].中国电机工程学报，2015，35(20)：5278-5285.Li Yong，Mai Ruikun，Lu Liwen，et al.A harmonic elimination and power regulation approach of a cascaded multilevel technology in IPT systems[J].Proceedings of the CSEE，2015，35(20)：5278-5285.

[15]Hao Hao，Covic G，Kissin M，et al.A parallel topology for inductive power transfer power supplies[J].IEEE Applied Power Electronics Conference & Exposition，2011，29(3)：2027-2034.

[16]Ye Zhongming，Jain P K，Sen P C.Circulating current minimization in high-frequency AC power distribution architecture with multiple inverter modules operated in parallel[J].IEEE Transactions on Industrial Electronics，2007，54(5)：2673-2687.

[17]Boys J T，Covic G A，Green A W.Stability and control of inductively coupled power transfer systems[J].IEE Proceedings-Electric Power Applications，2000，147(1)：37-43.

[18]马俊鹏，宋文胜，冯晓云.单相三电平脉冲整流器无锁相环直接功率控制[J].中国电机工程学报，2015，35(7)：1723-1731.

Ma Junpeng，Song Wensheng，Feng Xiaoyun.Direct power control of single-phase three-level rectifiers without phase locked loop[J].Proceedings of the CSEE，2015，35(7)：1723-1731.

[19]Hu Aiguo Patrick.Selected resonant converters for IPT power supplies[D].Auckland：University of Auckland，2001.

[20]蔡华，史黎明，李耀华.感应耦合电能传输系统输出功率调节方法[J].电工技术学报，2014，29(1)：215-220.

Cai Hua，Shi Liming，Li Yaohua.Output power adjustment in inductively coupled power transfer system[J].Transactions of China Electrotechnical Society，2014，29(1)：215-220.

[21]Dieckerhoff S，Ruan M J，De Doncker R W.Design of an IGBT-based LCL-resonant inverter for high-frequency induction heating[C]//Conference Record of the 1999 IEEE Industry Applications Conference，Phoenix，AZ，1999，3：2039-2045.

[22]Schonknecht A，De Doncker R W.Novel topology for parallel connection of soft switching，high power，high frequency inverters[C]//Conference Record of the 2001 IEEE Industry Applications Conference，Chicago，IL，USA，2001，3：1447-1482.

Circulating Current Elimination of Parallel Dual-inverter for IPT Systems

Mai RuikunLu LiwenLi Yong

(Key Laboratory of Magnetic Suspension Technology and Maglev VehicleMinistry of Education Chengdu610031China)

A phasor control method is employed in this paper to eliminate the circulating current caused by the parallel connected high frequency inverters.The topology of the parallel dual-inverter LCCL-based inductive power transfer (IPT) system and the cause of circulating current are analyzed in detail.Secondly, the virtual active/reactive power based on the current of the primary coil are calculated without using the phase-locked loop, the relationship between the goal of the phasor control and the virtual active/reactive power is analyzed, and then the circulating current eliminating approach is provided.The performance of the proposed approach is evaluated by the experimentation of two parallel connected high frequency inverters with 1.4 kW maximum transmission power and overall 89.82% DC-DC transmission efficiency.The experimental results demonstrate that the circulating current between the parallel connected inverters is dramatically reduced by the proposed algorithm.

Parallel high-frequency inverters technology，inductive power transfer，phasor control，circulating current eliminating，virtual active/reactive power

2015-05-25改稿日期2015-11-25

TM464

麦瑞坤男，1980年生，副教授，博士生导师，研究方向无线电能传输技术及其控制。

E-mail：82009003@qq.com(通信作者)

陆立文男，1990年生，硕士研究生，研究方向为大功率无线电能传输技术及其控制。

E-mail：953390550@qq.com

国家自然科学青年基金(51507147)、铁路总公司科技研究开发计划课题(2014J013-B)和中央高校基本科研业务费专项资金(2682015CX021)资助项目。