一种基于与非锥簇架构FPGA输入交叉互连设计优化方法

2016-10-14黄志洪杨立群江政泓杨海钢

电子与信息学报 2016年9期

黄志洪李威杨立群江政泓魏星林郁杨海钢

黄志洪①②李威①杨立群①②江政泓①②魏星①②林郁①杨海钢*①

①(中国科学院电子学研究所北京 100190)②(中国科学院大学北京 100190)

该文针对与非锥(And-Inverter Cone, AIC)簇架构FPGA开发中面临的簇面积过大的瓶颈问题，对其输入交叉互连设计优化进行深入研究，在评估优化流程层次，首次创新性提出装箱网表统计法对AIC簇输入和反馈资源占用情况进行分析，为设计及优化输入交叉互连结构提供指导，以更高效获得优化参数。针对输入交叉互连模块，在结构参数设计层次，首次提出将引脚输入和输出反馈连通率分离独立设计，并通过大量的实验，获得最优连通率组合。在电路设计实现层次，有效利用AIC逻辑锥电路结构特点，首次提出双相输入交叉互连电路实现。相比于已有的AIC簇结构，通过该文提出的优化方法所得的AIC簇自身面积可减小21.21%，面积制约问题得到了明显改善。在实现MCNC和VTR应用电路集时，与Altera公司的FPGA芯片Stratix IV(LUT架构)相比，采用具有该文所设计的输入交叉互连结构的AIC架构FPGA，平均面积延时积分别减小了48.49%和26.29%；与传统AIC架构FPGA相比，平均面积延时积分别减小了28.48%和28.37%，显著提升了FPGA的整体性能。

与非锥(AIC); AIC簇；装箱网表统计法；连通率；分类独立设计；双相输入交叉互连

1 引言

FPGA(Field-Programmable Gate Arrays)自1984年诞生以来，发展至今已成为数字电路系统的核心器件。FPGA灵活的可编程能力使得其能够实现各种逻辑功能，满足不同领域用户的功能需求，其开发周期短，容易升级的特点更适用于技术不断革新的市场应用。当前主流的商用FPGA器件基本都采用孤岛型结构[3]，逻辑功能普遍通过查找表(Look up Table, LUT)结构[4]实现，位输入的查找表能够实现种功能。查找表结构逻辑单元强大的可编程能力推动了FPGA的快速发展和广泛应用，然而其高度灵活性也带来了面积和性能的开销，且其本身的可扩展性约束也随着工艺节点的不断进步逐渐凸显，如何改进LUT结构进一步提升FPGA性能一直是学术界和工业界的研究焦点。

2012年，文献[8,9]提出了一种基于与非锥结构的新型FPGA逻辑单元。其核心思想是利用综合工具如abc[10]中的Boolean SAT技术方案[11]，使得电路在映射成为有向无环图AIG(And-Inverter Graph)时能够在不同深度上找到大量可复用的子图，而AIC架构FPGA能够提供可复用的逻辑单元，从而最大程度地提高逻辑资源利用率。

2014年第22届FPGA国际会议上，文献[12]首次尝试通过标准CMOS工艺实现基于AIC架构的FPGA电路设计，通过实验仿真获得性能参数，并提供结构参数和模型输入VTR[13]架构评估工具，以获得待评估电路集中不同电路的面积、时延性能，并得出结论：LUT和AIC结构在不同应用电路上各有优劣，基于AIC架构的FPGA在平均时延性能上更优，但面积相对较大。文献[12]中输入交叉互连模块(input crossbar)占到了整个逻辑簇面积的62.77%，而真正的功能逻辑和时序电路模块仅占到AIC簇面积的10.3%，庞大的输入交叉互连模块直接导致AIC架构逻辑簇面积过大的缺陷。

本文首次采用统计方法对映射装箱后的应用电路网表资源利用率进行计算分析，利用分析结果指导输入交叉互连结构设计，并提出将AIC簇的输入引脚和输出反馈连通率分离独立设计，在电路实现层次，提出一种双相输出交叉矩阵，以优化AIC FPGA的实现性能。通过集成了改进的面向AIC结构映射工具[14]的完整高效FPGA架构评估流程，经过大量的仿真、优化和实验，获得一种优化的适用于AIC簇架构FPGA的输入交叉互连结构。

2 AIC逻辑簇及输入交叉互连模块

AIC基本单元的结构如图1中BAE(Basic AIC Element)所示，多级AIC逻辑锥由多层次的基本单元BAE组成，其中，第1级采用改进型可编程AIC单元(Enhanced AIC Element, EAE)即在各输入端加入正反信号选择模块，使第1级AIC即能实现,,,,,,,8种逻辑功能。

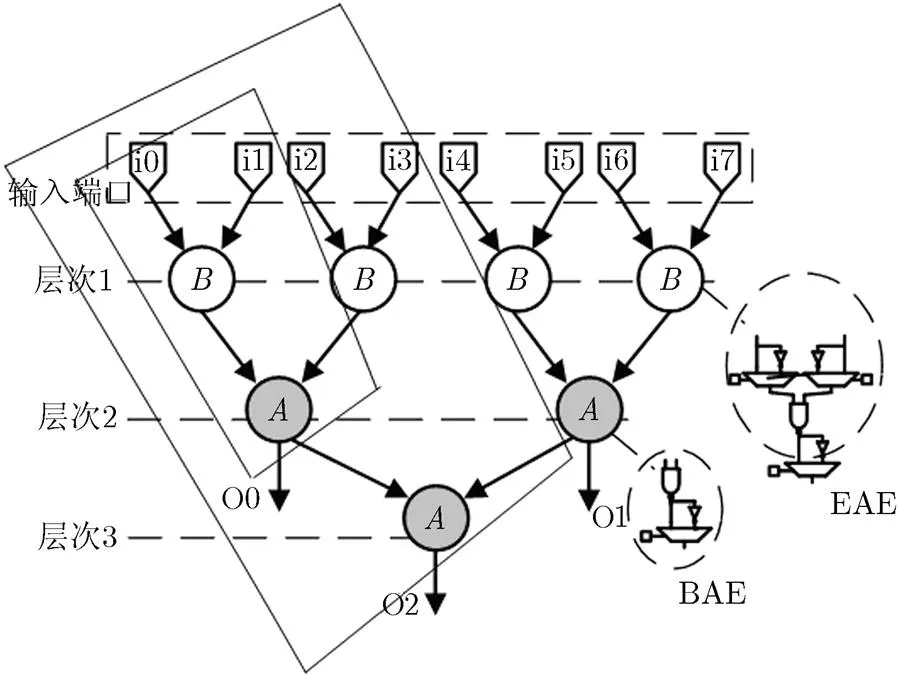
图1 AIC逻辑单元及AIC逻辑锥

根据德摩根律[15]，任何函数功能通过逻辑运算都能够通过运算转换成与非单元的组合表达式。因而可将任意的函数映射到AIC组合结构上。

AIC逻辑锥区分于传统查找表结构的一个重要特点是其在各级中间层次可具有多个输出，因而能够最大程度上复用资源实现映射生成的重复子图单元，从而在提高资源利用率的同时提升性能。

AIC逻辑簇是由一个或者多个AIC锥通过局部互连组成的可编程逻辑模块，与基于LUT结构的LAB模块相对应。在文献[12]中为了实现与主流商用FPGA进行比对，采用了全定制设计方法，在Cadence的Virtuso设计平台上，通过40 nm标准CMOS工艺实现了Altera公司Stratix-IV的逻辑功能簇[16]作为对比的参照基准，性能与实际芯片数据相近。

该AIC逻辑簇由3个层次为6的AIC逻辑锥(AIC6)组成，每个AIC6有64个输入端，由第2级开始输出，称为AIC6_2。通道提供了64个输入引脚，经过输入交叉互连模块选择后，为3个AIC6_2提供192个输入。每个AIC6_2共31个输出，通过中间交叉互连模块选择后，可选择是否连接到寄存器DFF实现时序或者直接提供组合逻辑输出，再经过输出交叉互连模块将数目减少到20并最终输出到全局互连通道资源。

文献[12]中的AIC逻辑簇与传统LUT结构逻辑簇相比，在平均延时性能上有一定优势，但电路实现平均面积较差。深入分析该AIC簇结构，由于AIC簇拥有多输入多输出的结构特点，使得其能较快处理多输入信号，而且多层次中间节点输出的存在使得其能够复用逻辑运算模块的中间结果，从而提高逻辑运算密度和利用率。但丰富的局部布线资源也意味着资源的冗余和面积、延时代价。统计结果可得，文献[12]中局部互连资源(input/middle/ output crossbar)占整个AIC簇结构中面积的79.89%，延时占AIC簇总延时43.3%至70.7%。

由于映射工具受限等因素，如原映射工具在映射阶段没有合理考虑不同单元的映射代价，且仅支持AIC每个层次都需输出，直接导致输出数目的倍增，限制制约了AIC簇设计的灵活性。针对这些问题，我们基于开源的abc软件对新的工艺映射工具进行了开发[14]，引入了映射单元库，建立映射代价函数，在映射阶段即考虑不同映射结果的代价，并在大量的候选映射划分中，选择最优的映射方案，同时实现AIC逻辑簇的输入、输出层次、输出个数独立可调节，使得结构设计能有更大的自由空间，选择更为合理的方式。

通过限制AIC6从第3级开始输出,并简称该与非锥为AIC6_3，其输出数目即可降为15，原AIC逻辑簇中的中间输出交叉互连和输出交叉互连即可移除，AIC逻辑簇结构改进部分为图2阴影部分所示。

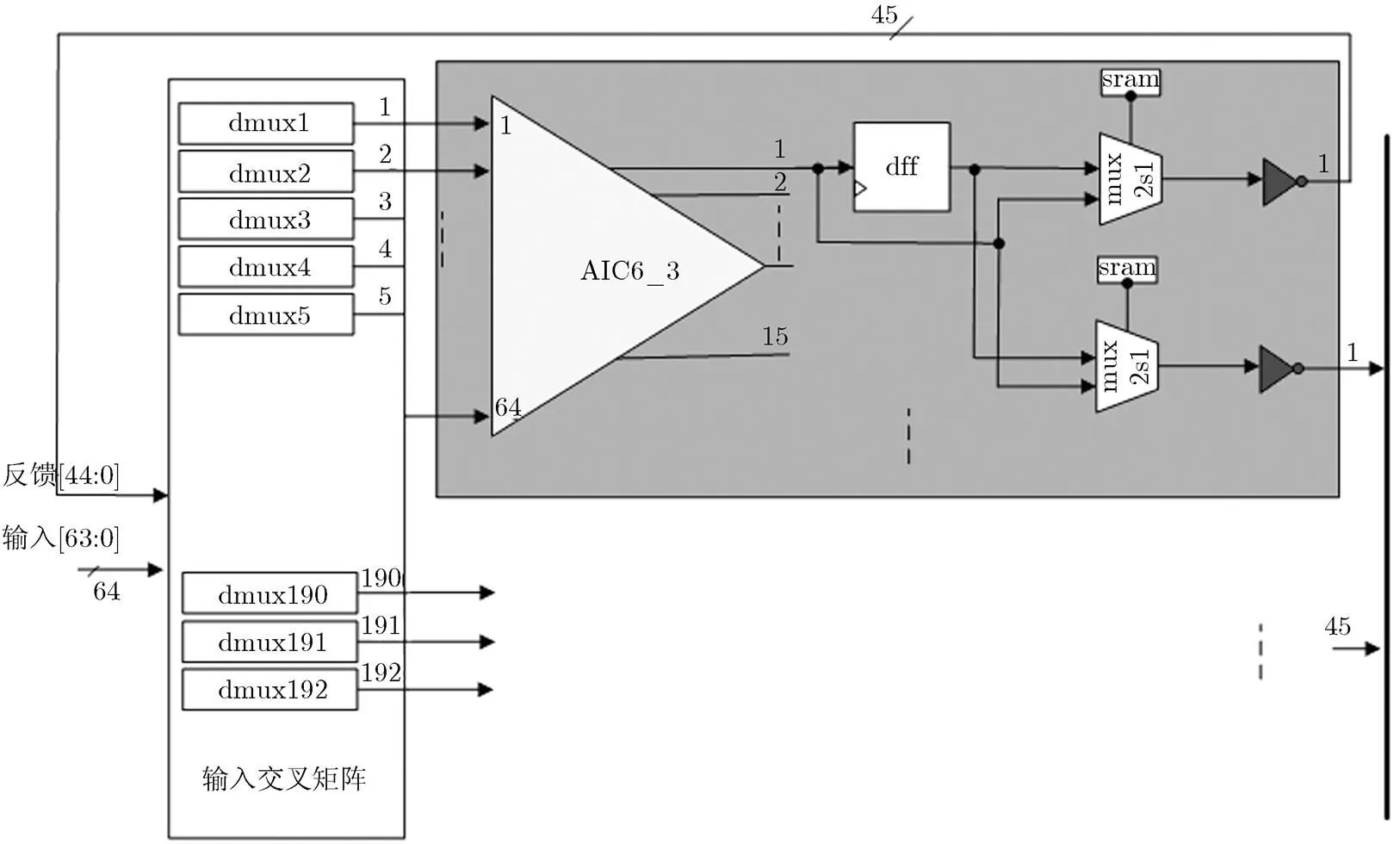
图2 限制AIC6的输出级数为3的AIC簇及输入交叉互连

限制AIC6输出级数后可以移除中间和输出交叉互连模块，但输入交叉互连模块仍然必须保留，以保障为AIC逻辑功能块提供丰富的输入资源。而此时，输入交叉互连模块占用整个AIC簇面积的比例则更加凸显，高达73.89%，延时则占整个AIC簇逻辑的24.14%~50.2%。因此如何合理改进输入交叉互连模块，设计高效的互连关系，采用优化的电路实现方式，成为了AIC逻辑簇整体性能得到进一步提高的关键。

3 AIC簇输入交叉互连模块结构设计

3.1 AIC簇互连结构参数评估流程

本文对AIC簇输入交叉互连模块结构参数评估采用的CAD流程如图3所示。所建立的完整流程包括：通过设定预设结构参数，电路设计、仿真验证、管子参数优化，获得映射单元面积和时延库，以提供工艺映射过程建立合理代价函数，获得电路基本结构参数以提供装箱及后续步骤，建立延时和面积模型以提供布局布线过程，对应用电路的实现面积和时延信息进行评估，以确定最优的结构参数。

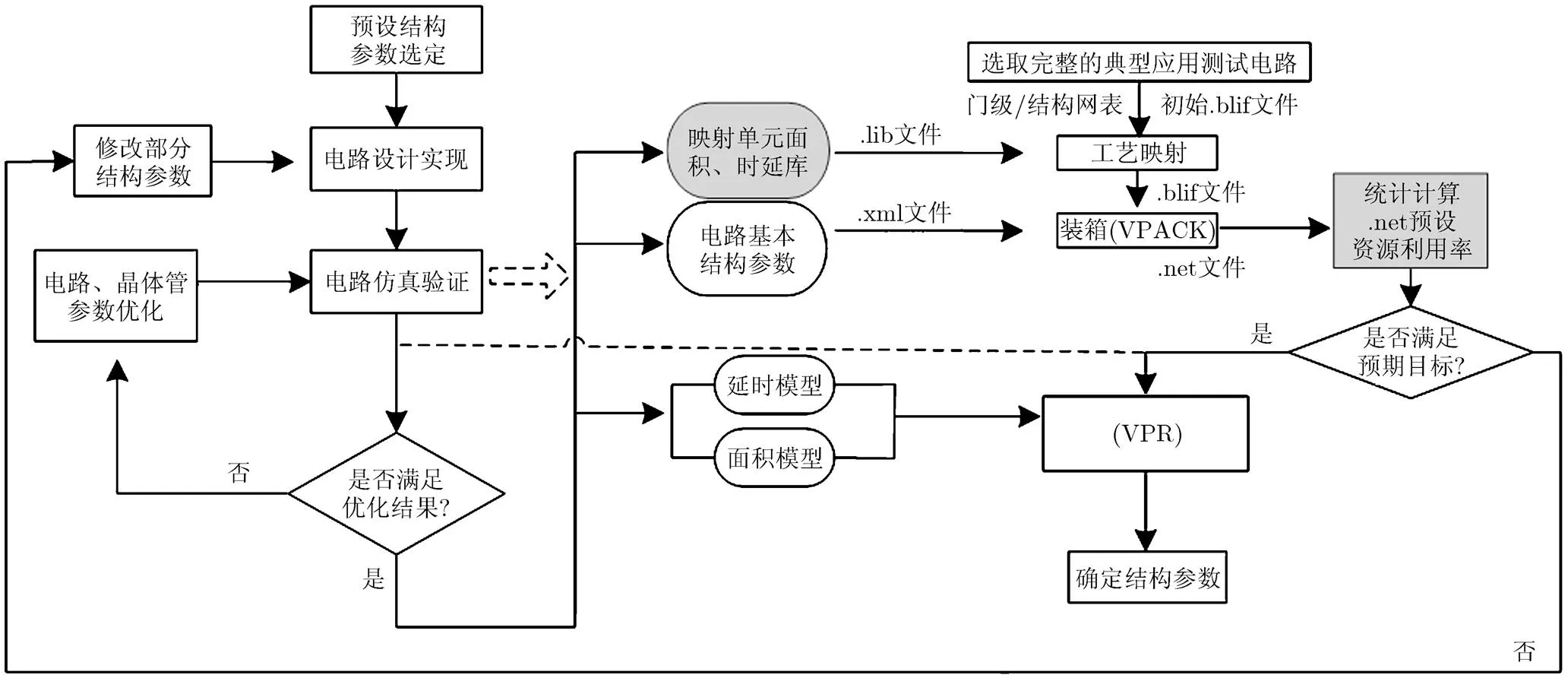
图3 AIC簇输入交叉互连结构评估CAD流程

本文采用学术界公认的经典20个最大的MCNC电路[17]和VTR中的大部分电路[18]，除去个别规模过大非常耗时的电路，作为典型应用测试电路集，进行架构参数评估。与通用的VTR7.0流程[13]相比，工艺映射过程集成了所开发的针对AIC结构的改进型映射工具，而且在采用VPR进行布局布线过程前，开发统计工具，统计计算网表预设资源利用率，并返回指导修改结构参数，以加速确定优化的结构参数。

流程采用全定制设计，采用40 nm 标准CMOS工艺以保持与stratix-IV以及文献[12]中一致，设计平台为Cadence公司的Virtuso开发套件，仿真验证、管子优化过程采用spectre工具进行，参数处理也采用和文献[12]中相同的方式，以确保数据和实际芯片相近，且具有可比性。

3.2输入交叉互连模块结构参数及连通率分类独立设计

深入分析输入交叉互连模块，设定其输入端引脚个数为，输出反馈个数为，输出个数为，输入交叉互连模块输入到每个输出的连通率为。在图2中的阴影部分逻辑功能确定的情况下，为了使每个AIC6能够有充分的输入逻辑资源，需保持输入端引脚个数为64，同样为了实现每个AIC6输入端来源的独立性，输出个数需为192，而输出反馈的个数也固定为45。合理设计输入交叉互连模块的连通率成为了优化设计的关键。

文献[12]中设定的连通率为50%，本文为了更精细地对输入交叉互连模块的连接关系进行设计，将输入引脚到每个输出端的连通率定义为，输出反馈到每个输出端的连通率定义为。本文首次提出将AIC逻辑簇输入交叉互连模块的输入和反馈连通率独立分离设计，从而避免了文献[12]中存在的二者必须保持相同比例的设计约束，实现对和的独立设计和组合，以获取更为高效的输入交叉互连关系。

3.3 装箱网表统计法

由于不同结构参数组合的设计空间非常大，而且对输入交叉互连模块而言，不同连通率对应着不同的电路实现，而每种电路需经过设计实现、仿真验证、管子参数优化，才能提供相关的结构参数进行后续的CAD评估流程。这一过程将多次循环往复，直至找到最优的设计方案，因此将耗费大量的运算资源和时间。

为了能够更高效迅速确定优化的结构参数范围，本文针对AIC簇输入交叉互连结构的优化设计，提出一种装箱网表统计法，即先设定合理的较为宽裕互连资源参数，通过电路设计仿真，获得相关信息，提供综合映射装箱后，对.net网表进行资源统计分析，以确定提供的资源的利用率，根据所得信息返回对原设定的结构参数进行修改，再循环重复上述流程，以加快确定最优化结构参数。虽然无法通过统计结果直接确定最优化的结构参数数值，但可以更合理和准确地指导参数的选择。

文献[12]中的AIC簇的输入交叉互连为50%时，面积和延时都过大。本文预设和均为50%，根据图3实验流程，完成电路设计及仿真优化，提供所需信息文件，将应用电路集进行映射、装箱，得到.net格式网表文件，通过网表资源统计工具计算分析可得，在占用的AIC簇中，应用电路集平均每个AIC簇占用了46.67个引脚输入，4.78个输出反馈，VTR应用电路集平均每个AIC簇占用了22.27个引脚输入，4.90个输出反馈。整个测试电路集平均每个AIC簇占用了34.47个引脚输入，4.84个输出反馈，即引脚输入约占总引脚输入的53.84%，反馈个数约占总输出反馈的10.76%。对比预定结构所提供的和，可以发现的选定在一定的合理区间，而则有着较大的资源冗余。故返回指导预定结构参数进行对应修改。

3.4 结构参数实验结果

由于输入交叉互连模块电路本身设计对称性，以及驱动和负载一致性的要求，使得连通率的选定有一定的限制，因此无法设定任意的连通率值。本文采用的实验方法如下：先固定结构参数中的为50%，对的最优值进行实验，拟定的选值为50%, 33%, 25%, 12.5%, 6.25%, 0%，按照图3所示的流程，在选用不同取值后，进行电路的设计和仿真，但跳过晶体管尺寸的优化循环，留待最优参数结构组合确定后，再进一步进行晶体管参数优化，以高效完成CAD结构评估。

通过完整的CAD评估流程和大量实验，可得MCNC和VTR应用电路集在基于不同反馈连通率值的输入交叉互连模块的AIC架构FPGA上实现关键路径延时和面积，与Stratix-IV和文献[12]中AIC结构相比，测试电路集平均面积、延时、面积延时积归一化比例如图4所示。

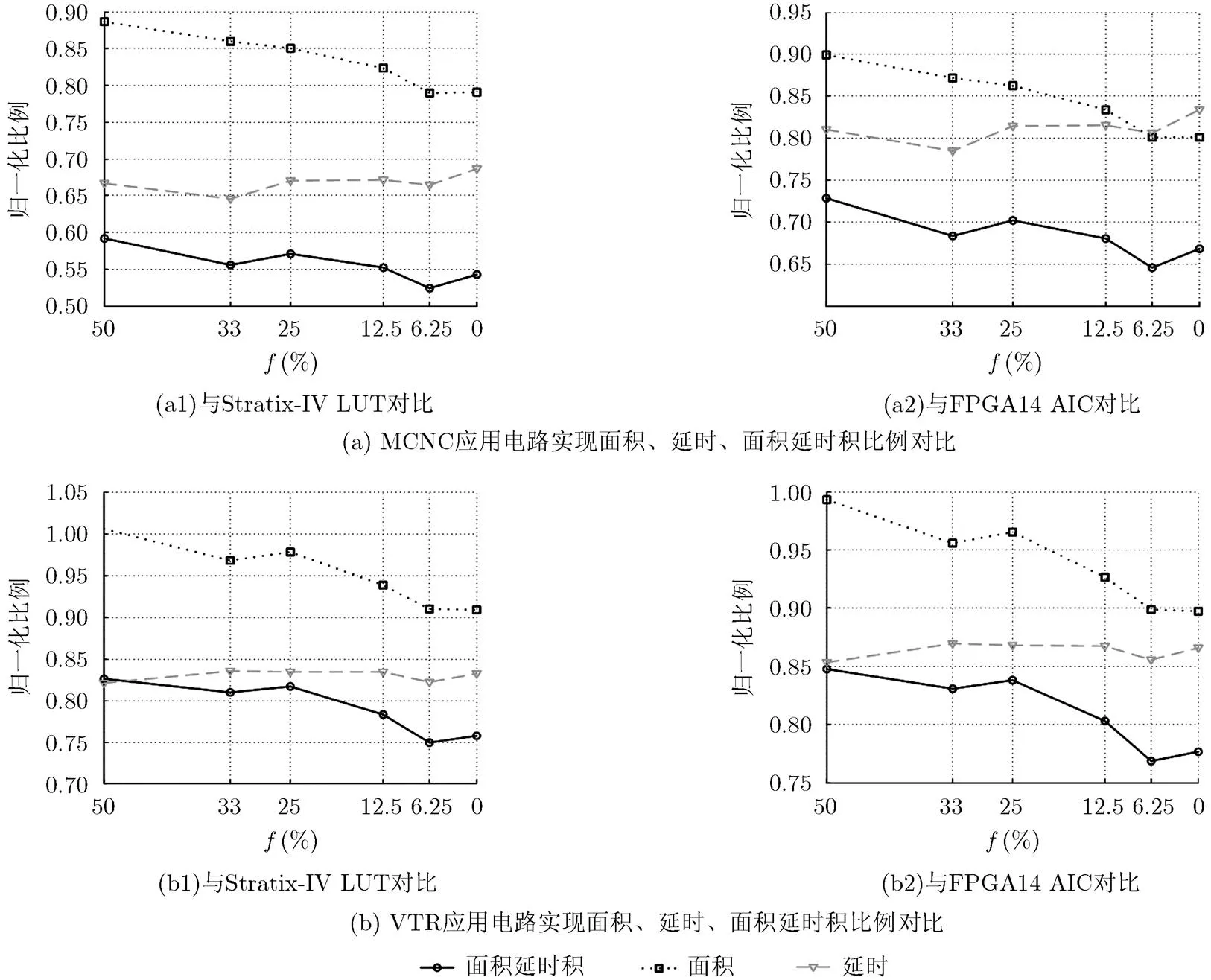
图4 面积、延时、面积延时积随f变化图

分析图4可得，当为6.25%时，无论是MCNC还是VTR应用电路集，其实现的电路面积延时积都达到最优，两组测试电路集有着相同的结论。

故本文选定6.25%作为的预设值，对的取值进一步进行实验评估。类似地，拟定的选值为56%, 53%, 50%, 47%, 44%, 41%, 38%, 34%, 31%作为结构参数测试点，通过完整的CAD评估流程和大量实验，可得MCNC和VTR应用电路集在基于不同输入引脚连通率值的输入交叉互连模块的AIC架构FPGA上实现关键路径延时和面积，与Stratix-IV和文献[12]中AIC结构相比，测试电路集平均面积、延时、面积延时积归一化比例如图5所示。

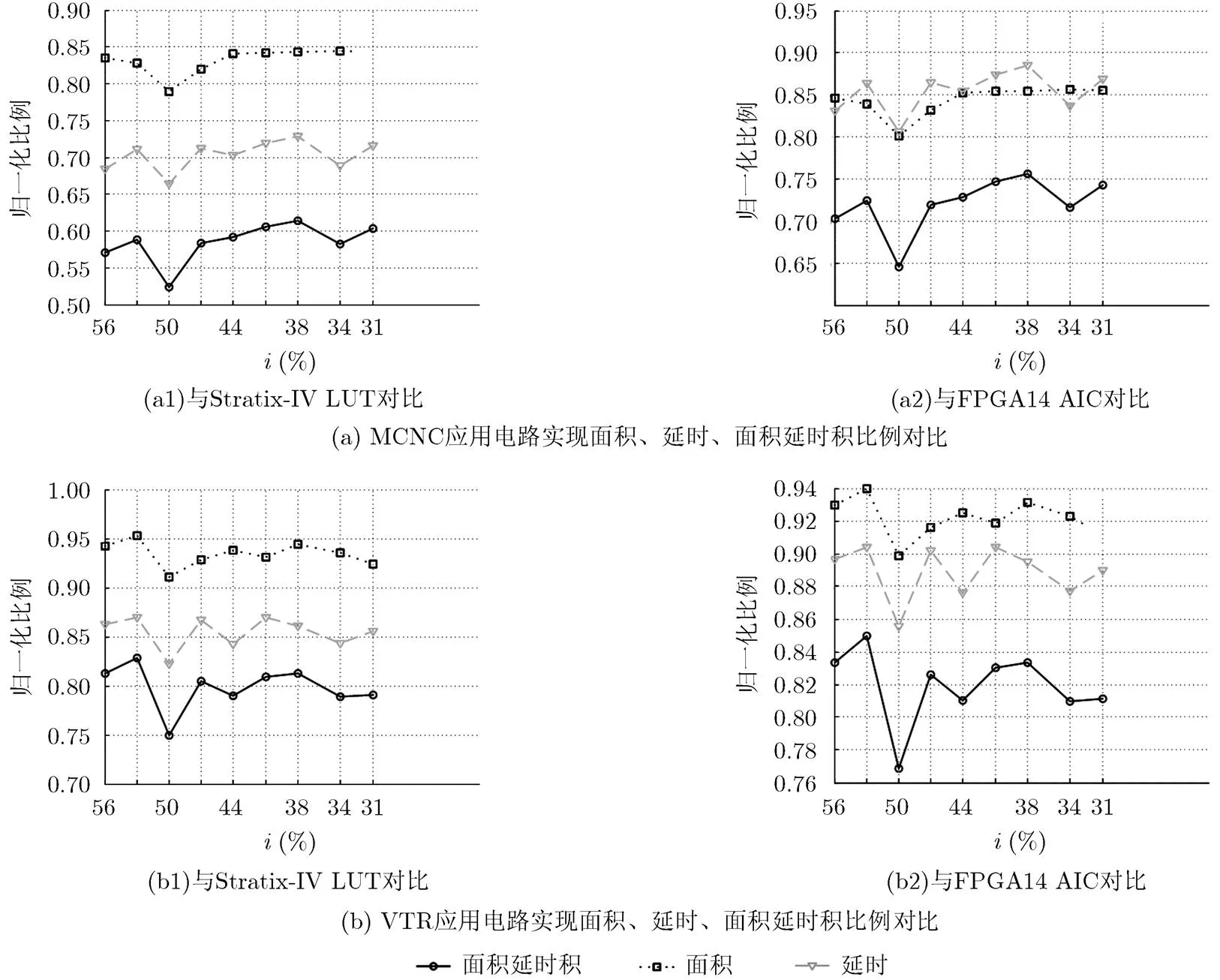
图5 面积、延时、面积延时积随i变化图

分析图5可得，当为50%时，无论是MCNC还是VTR应用电路集，其实现的电路面积延时积都达到最优，两组测试电路集同样有着相同的结论。

因此，我们可以得出结论，在当前拟定的设计架构下，当AIC簇输入交叉互连模块的输入引脚连通率取50%，反馈连通率取6.25%时，FPGA有着最优的面积延时积性能。这一结论也进一步证实了装箱网表资源统计结论方向的正确性。

按照图3所示流程，进一步采用优化的参数结构，对电路设计实现进行晶体管级优化，修改面积和时延参数，再次进行装箱，VPR等步骤，统计分析以得到在该设计最优化结构下的电路关键路径延时和面积。

和文献[12]中的AIC簇结构相比，采用该输入交叉互连模块，AIC簇本身的电路延时减小了21.24%，电路实现面积减少了20.28%，输入交叉互连模块实现面积较大的突出问题得到了明显改善。

相比于Stratix-IV的LUT结构，该AIC簇结构实现MCNC和VTR应用电路集在平均面积延时积上分别提升了48.12%和25.86%；相比于文献[12]中原有的AIC结构，则分别提升了27.97%和27.95%。

3.5 双相输入交叉互连电路实现

在文献[12]中，各级交叉矩阵的电路实现方式均采用二级阵列多路选择器电路实现，与主流的Altera公司的Stratix系列产品相似[19]。

深入分析图1中的AIC簇架构，可以发现，每个AIC6的输入端均需经过一个反相器实现反向，以便通过编程选择输入的极性。综合考虑交叉矩阵和EAE电路结构，针对输入交叉互连模块，本文提出双相输入交叉互连电路实现方式，为每个AIC逻辑锥同时提供正向和反向的输入，其每个多路选择器的电路实现方式如图6所示。

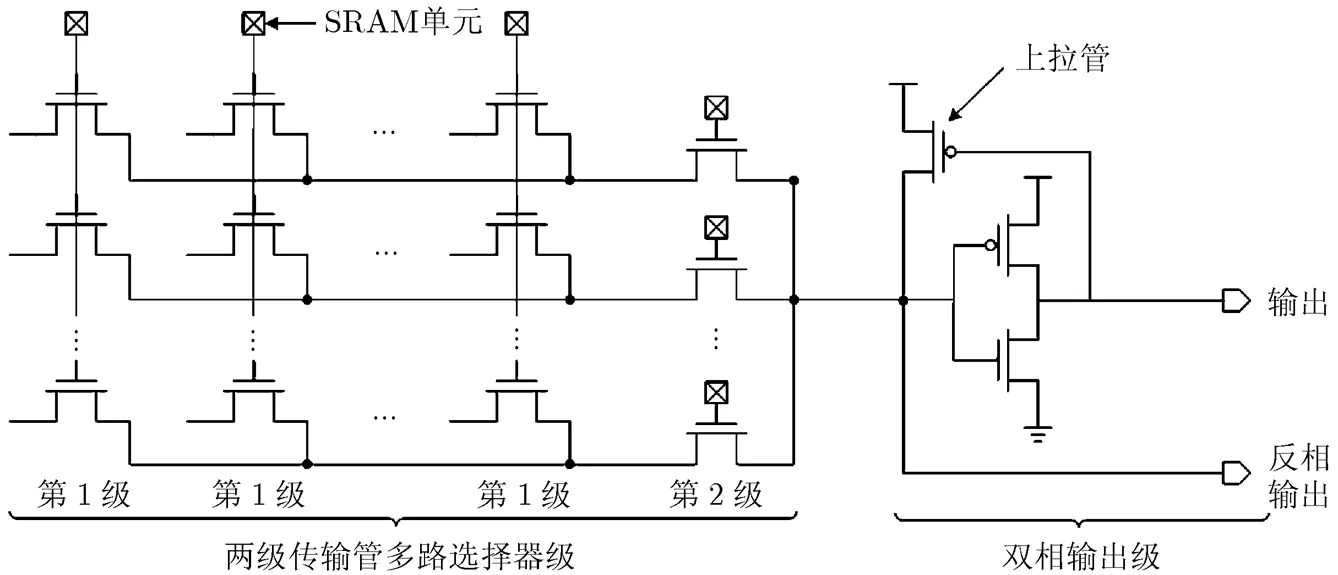
图6 双相输入交叉互连多路选择器电路

通过管子优化设计，Spectre仿真验证，其正向路径延时性能同原设计相当。反向延时路径虽然相比原设计电路减少了两级反相器，但由于该电路采用传输管结构实现，中间电平压降效应影响了信号的上升时间，其最终延时也同原设计相近。然而采用了双相输入交叉模块，可以将AIC逻辑锥第1层输入端的反向器移除，达到了进一步减小整个AIC簇实现面积的目的。

采用双相输入交叉互连实现的AIC簇在本身实现面积上进一步减小了4.8%，整个AIC簇面积相比于文献[12]中的AIC簇减少了21.21%。

通过CAD评估流程，可得最终在MCNC和VTR应用电路集实现面积和关键路径延时比对如表1所示。

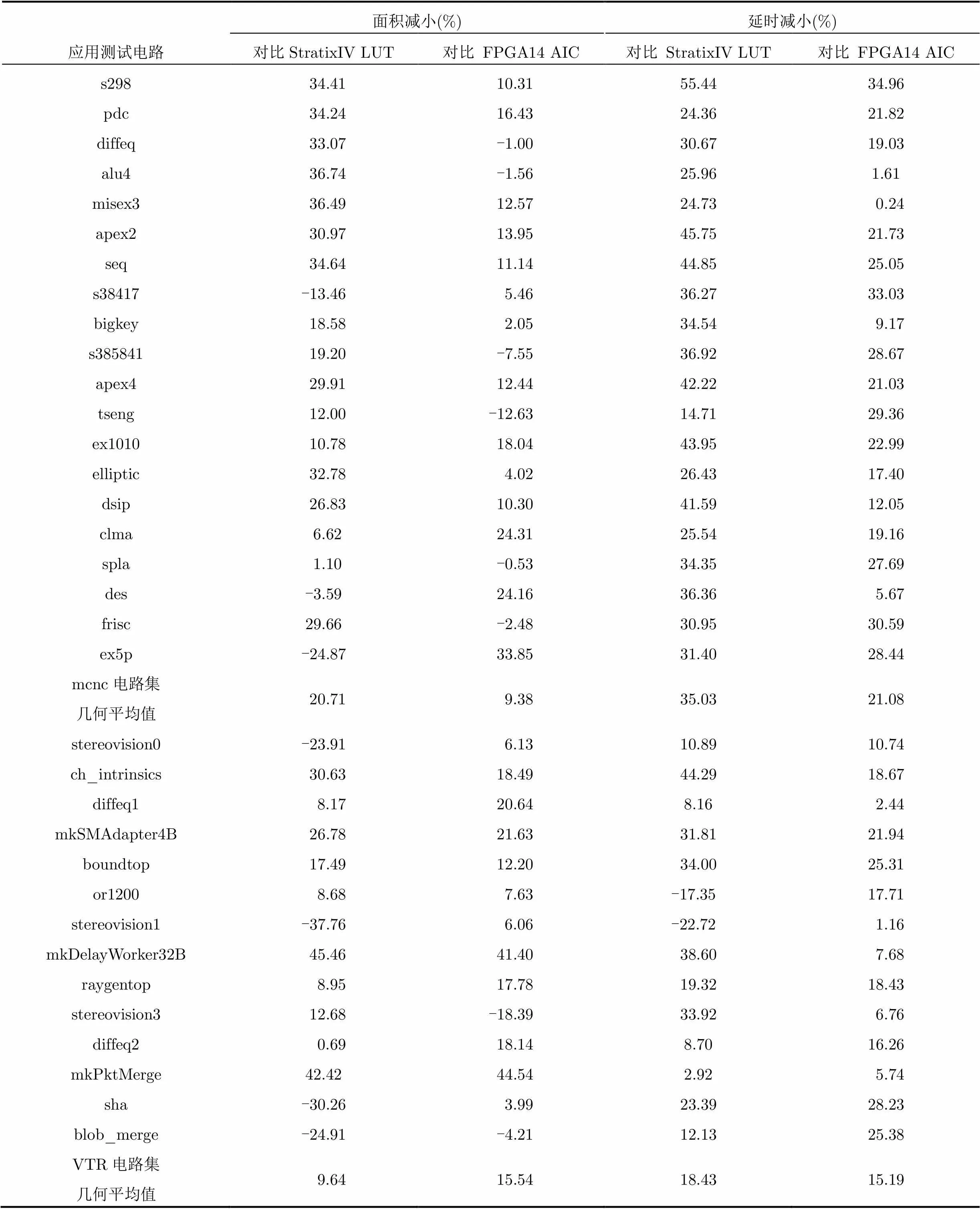
表1采用双相输入交叉互连电路实现的AIC簇结构面积和延时减小比例

与Stratix-IV结构相比，采用本文所提出的双相输出交叉互连电路实现的AIC簇结构在MCNC和VTR应用电路集平均面积延时积分别减小了48.49%和26.29%；与文献[12]中AIC结构相比，平均面积延时积分别减小了28.48%和28.37%。

4 结论

本文针对AIC架构FPGA开发中出现的实现面积过大的问题，深入分析其症结根源，对输入交叉互连结构的设计优化进行探索。本文建立了适用于AIC架构输入交叉互连模块结构参数评估的高效优化CAD流程，创新性提出装箱网表统计法对资源占用情况进行分析，并利用所得结果对输入交叉互连结构参数的优化提供指导，以更高效获取优化参数。在结构参数设计层面，首次提出将引脚输入和输出反馈连通率分离独立设计的思想，并通过大量的实验，获得最优化结构参数组合。在电路实现层次，结合AIC逻辑锥结构特点，首次提出双相输入交叉互连电路实现方式，进一步缩小了AIC簇的面积，相比于文献[12]中的AIC簇结构，本文所提出的优化AIC簇本身实现面积可减小21.21%，从而在有效解决了AIC架构FPGA的面积困扰问题，也使得AIC架构FPGA展现出了其潜在的优势和广阔的进一步优化空间。

经过大量的电路仿真、优化、实验，通过完整CAD流程得到优化结果。与Stratix-IV结构相比，采用本文所提出的输入交叉互连结构的AIC架构FPGA，在MCNC和VTR应用电路集平均面积延时积分别减小了48.49%和26.29%；与文献[12]中AIC结构相比，平均面积延时积分别减小了28.48%和28.37%，显著提升了FPGA芯片的整体性能。

[1] CHINNEY D and KEUTZER K. Closing the Gap Between ASIC and Custom: Tools and Techniques for High-performance ASIC Design[M]. Netherland, Kluwer Academic Publishers, 2002: 157-158.doi: 10.1007/b105287.

[2] FRITZ Mayer-Lindenberg. Design and application of a scalable embedded systems’ architecture with an FPGA based operating infrastructure[C]. 9th Euromacro Conference on Digital System Design, Croatia, 2006: 189-196. doi: 10.1109/DSD.2006.39.

[3] BROWN S D, FRANCIS R, ROSE J,. Field Programmable Gate Arrays[M]. Netherland, Kluwer Academic Publishers, 1992: 127-133. doi:10.1007/978-1- 4615-3572-0.

[4] BETZ V, ROSE J, and MARQUARDT A. Architecture and CAD for Deep-Submicron FPGAs[M]. Netherlands, Kluwer Academic Publishers, 1999: 15-20. doi:10.1007/978-1-4615- 5145-4.

[5] HUTTON M, SCHLEICHER J, LEWIS D,Improving FPGA performance and area using an adaptive logic module [C]. IEEE International Conference on Field Programmable Logic and Applications (FPL), Belgium, 2004: 135-144. doi:10.1007/978-3-540-30117-2_16.

[6] AHMED E and ROSE J. The effect of LUT and cluster size on deep-submicron FPGA performance and density[J].(), 2004, 12(3): 288-298. doi: 10.1109/FPGA.2000.38.

[7] JIANG Z, LIN Y, YANG L,. Exploring architecture parameters for dual-output LUT based FPGAs[C]. IEEE International Conference on Field Programmable Logic and Applications (FPL), Munich, 2014: 436-441. doi: 10.1109/ FPL.2014.6927470.

[8] PARANDEH-AFSHAR H, BENBIHI H, NOVO D,. Rethinking FPGAs: elude the flexibility excess of LUTs with and-inverter cones[C]. Proceedings of the ACM/SIGDA International Symposium on Field Programmable Gate Arrays, Monterey, 2012: 119-128. doi:10.1145/2145694. 2145715.

[9] PARANDEH-AFSHAR H, ZGHEIB G, NOVO D,. Shadow and-inverter cones[C]. IEEE International Conference on Field Programmable Logic and Applications (FPL), Porto, 2013: 1-4. doi: 10.1109/FPL.2013.6645566.

[10] BRAYTON R and MISHCHENKO A. ABC: An academic industrial-strength verification tool[C]. Computer Aided Verification, Edinburgh, 2010: 24-40. doi: 10.1007/978-3- 642-14295-6_5.

[11] MISHCHENKO A, CHATTERJEE S, and BRAYTON R. DAG-aware AIG rewriting: A fresh look at combinational logic synthesis[C]. Proceedings of the 43rd Design Automation Conference, San Francisco, 2006: 532-536. doi: 10.1145/1146909.1147048.

[12] ZGHEIB G, YANG L, HUANG Z,. Revisiting and-inverter cones[C]. Proceedings of the 2014 ACM/SIGDA international symposium on Field-Programmable Gate Arrays. ACM, Monterey, 2014: 45-54. doi: 10.1145/2554688. 2554791.

[13] LUU J, GOEDERS J, WAINBERG M,. VTR 7.0: next generation architecture and CAD system for FPGAs[J].(), 2014, 7(2): 6:1-6:30. doi: 10.1145/ 2617593.

[14] 江政泓, 林郁, 黄志洪, 等. 面向AIC结构的FPGA映射工具[J].电子与信息学报, 2015, 37(7): 1769-1773. doi: 10. 11999/JEIT141403.

JIANG Z, LIN Y, HUANG Z,. Mapper for AIC-based FPGAs[J]&, 2015, 37(7): 1769-1773. doi: 10.11999/JEIT141403.

[15] 埃伯哈德, 蔡德勒等, 编. 李文林, 等译.《数学指南—实用数学手册[M]. 北京:科学出版社, 2012: 875.

[16] Altera Corporation. Stratix IV Device Handbook, Vols.1 and 2. [OL]. https://www.altera.com/content/dam/altera-www/ global/en_US/pdfs/literature/hb/strastr-iv/stratix4_handbook.pdf, 2012.

[17] YANG S. Logic synthesis and optimization benchmarks, User Guide, version 3.0[OL]. http://ddd.fit.cvut.cz/prj/ Benchmarks/LGSynth91.pdf, 1991.

[18] MURRAY K E, WHITTY S, LIU S,. Titan: Enabling large and complex benchmarks in academic CAD[C]. Proceedings of the 23rd International Conference on Field-Programmable Logic and Applications, Porto, Portugal, 2013: 1-8. doi:10.1109/FPL.2013.6645503.

[19] LEWIS D, AHMED E, BAECKLER G,. The stratix II logic and routing architecture[C]. Proceedings of the 2005 ACM/SIGDA 13th ACM International Symposium on Field- Programmable Gate Arrays, Monterey, 2005: 14-20. doi: 10. 1145/1046192.1046195.

An Input Crossbar Optimisation Method for And-inverter ConeBased FPGA

HUANG Zhihong①②LI Wei①YANG Liqun①②JIANG Zhenghong①②WEI Xing①②LIN Yu①YANGHaigang①

①(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)②(University of Chinese Academy of Sciences, Beijing 100190, China)

In order to break through the bottleneck of the huge cluster area in AIC (And-Inverter Cone) architecture based FPGA, the research on the optimisation of the input crossbar architecture is carried on. A post-pack netlist statistics method is creatively proposed to analyze the utilization of AIC cluster inputs and feedbacks and to guide the input crossbar design. And on the architecture parameter design level, it is firstly proposed to separately design the connective probability of the AIC cluster inputs and feedbacks. Through substantial experiments, optimum connective probability combination is derived. From the circuit implement view, dual-phases multiplexer input crossbar is presented according to the characteristics of AIC. The area of the AIC cluster, optimized through the proposed approach, achieves 21.21% smaller than the original one, the huge area problem is markedly ameliorated. When implementing the MCNC and VTR benchmarks, compared to Stratix IV, LUT based FPGA from Altera, the area-delay product of the AIC FPGA after optimisation is reduced by 48.49% and 26.29%, respectively. Compared to the original AIC-based FPGA architecture, the area-delay product is reduced by 28.48% and 28.37%, respectively.

And-Inverter Cone (AIC); AIC cluster; Post-pack netlist statistics; Connective probability; Separately design; Dual-phases multiplexer input crossbar

TN402

1009-5896(2016)09-2397-08

10.11999/JEIT151216

2015-11-25；

2016-04-27；

2016-04-14

国家自然科学基金(61271149)

The National Natural Science Foundation of China (61271149)

杨海钢 yanghg@mail.ie.ac.cn

黄志洪：男，1984年生，博士生，助理研究员，研究方向为可编程逻辑结构设计、嵌入式存储器通道结构.

李威：女，1983 年生，助理研究员，研究方向为可编程芯片结构设计.