计算共形几何简介
2016-10-14顾险峰
顾险峰, 雷 娜
(1.纽约州立大学石溪分校计算机系, 纽约11794; 2.大连理工大学软件学院, 辽宁大连116620)
计算共形几何简介
顾险峰1, 雷娜2
(1.纽约州立大学石溪分校计算机系, 纽约11794;2.大连理工大学软件学院, 辽宁大连116620)
计算共形几何是数学与计算机科学的交叉领域.本文介绍了计算共形几何中理论基础,计算方法及其在工程领域中的应用等.基本理论概念包括共形映射,单值化定理,共形模,拟共形映射,模空间等.基本计算方法包括调和映照方法,基于黎曼面理论的全纯微分方法,基于几何分析的曲面Ricci流方法.基本应用涵盖了医学图像,机械制造,数字媒体和虚拟/增强现实等领域.
共形几何; 黎曼面; 单值化; 调和映照; 全纯微分; 曲面Ricci流
1 引 言
几何是自然的语言,大自然亘古不变的伟大乐章是由几何谱写而成.对于深邃奥妙的几何真理的不懈追求是人类社会永恒的主旋律之一.几何理论和方法为人类提供了认识自然、改造自然的强有力的工具.依随人类对于几何真理的持续探索,基础理论的提炼和深化,人类认识到她的巨大审美价值,越来越多的人认识和体会到几何内在的优美和深刻.依随几何计算手段的建立和发展,人类认识到她的巨大实用价值,几何方法已经被广泛应用到社会实践的各个方面,极大地推动了生产力的发展.本文简单介绍共形几何的理论和方法在医疗和工程中的应用,使读者得以领略共形几何的简洁优美,和她解决实际问题的威力.
计算共形几何是一个交叉学科,根植于纯数学领域,例如黎曼面理论,复分析,微分几何,代数拓扑,偏微分方程等.计算共形几何已经被应用于计算机科学中的诸多领域,包括计算机图形学,计算机视觉,几何建模,医学图像和计算几何等.
历史上,计算共形几何也被广泛应用于工程领域[1],例如在电磁学,声学振动膜,弹性力学,热传导与流体力学等.这些应用绝大多数基于平面区域之间的共形变换.近来,随着三维扫描技术的发展,计算能力的提升,以及数学理论的进一步发展,人们已经把计算共形几何理论和算法从平面区域推广到了具有任意拓扑的度量曲面.
2 直观概览
所谓共形几何就是研究保角变换下不变量的一门学问,她为研究曲面间的变换和映射提供了理想的理论工具,而曲面比较和匹配在诸多工程和医疗领域中具有根本的重要性.图1显示了人脸曲面的保角映射的实例.左幅三维人脸曲面由三维扫描仪获取,右幅是保角映射的二维平面像.从图中可以看出,保角映射局部上是相似变换,虽然整体上具有很大的畸变,局部上是保持形状不变的.因此,保角变换又被称为是保形变换,或共形变换.

图1 人脸曲面的保角映射
图2显示了保角变换(共形变换)的几何特性.我们在二维圆盘中铺上不同的图案(称为纹理),由图1中的共形映射拉回到三维人脸曲面上,得到人脸曲面上不同的纹理贴图.如果纹理为黑白相间的棋盘格,如左幅图所示,棋盘格的四个角在人脸上依然是直角,这显示了共形映射保持角度不变.如果纹理为由许多彼此相切的微小圆形构成的模式,微圆在人脸上的像依然是微圆,这显示了共形映射保持无穷小圆不变.保角性和保圆性都是共形映射的本质特性.作为对比,图3显示了一个非共形映射的实例.同样的人脸,经由一般的微分同胚映到二维圆盘.圆盘上的微圆域被拉回成人脸上的椭圆域.人脸的几何特征没有被映射所保持,局部几何发生了很大的畸变.

图2 共形映射的保角和保圆特性
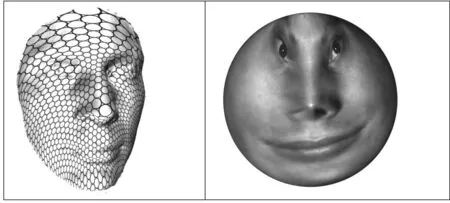
图3 非共形映射既不保圆,又不保形
人脸曲面到平面圆盘的共形映射并不唯一,两个共形映射之间相差一个莫比乌斯变换.单位圆盘到自身的所有共形映射都是莫比乌斯变换,所有的莫比乌斯变换构成一个三维的李群.图4展示了另一共形变换的实例,一张女孩的脸被共形地映到平面单位圆盘,不同的映射之间相差莫比乌斯变换.

图4 莫比乌斯变换
固定一个拓扑曲面,我们考察曲面上所有可能的黎曼度量.如果两个黎曼度量彼此相差一个标量函数,则这两个度量彼此共形等价.每个黎曼度量的共形等价类被称为是曲面的一个共形结构.拓扑曲面上所有的共形结构构成所谓的模空间.带有共形结构的曲面被称为是黎曼面.一个共形结构的全系不变量被称为是黎曼面的共形模.
人脸曲面是单联通的曲面,拓扑非常简单.对于一般曲面,其拓扑由是否可定向,环柄数目(亏格),边界数目所决定.单值化定理断言:所有带有黎曼度量的可定向曲面都可以共形地变换到三种标准空间中的一种:球面,欧氏平面和二维双曲空间.如图5所示,第一列为亏格为0的女孩雕塑表面,共形地映到球面上;第二列是亏格为1的小猫雕塑,它被周期性地共形地映到欧氏平面上.任意两个周期之间相差一个平移.第三列是高亏格的曲面,我们姑且称之为扭曲的双耳花瓶,它被周期性地共形地映到双曲平面上,任意两个周期之间相差一个莫比乌斯变换.莫比乌斯变换保持双曲长度不变,亦被称为双曲刚体变换.单值化定理在曲面几何理论中占据中心地位.

图5 封闭曲面单值化定理
带边界曲面的单值化定理如图6所示,曲面被共形映到标准空间去掉一些圆盘.大千世界,各种曲面千变万化,难以尽诉,但是万变不离其中.这一理论对于工程实践意义重大,这意味着所有三维几何处理的问题都可以转换为三种标准空间中的二维问题,这一转换极大地简化了问题的难度,增加了效率.
一般的微分同胚将无穷小圆映成无穷小椭圆,椭圆的偏心率(长短轴之比)和方向定义了Beltrami系数.基本上,映射和其Beltrami系数彼此相互决定.Beltrami系数的模有界的映射被称为是拟共形映射.拟共形映射给出了曲面间微分同胚的理论基础.

图6 带边界曲面单值化定理
3 计算方法
计算共形几何的计算方法丰富多彩,涉及到的数学分支非常广泛.我们以图5的单值化定理为例,来解释基本的计算方法.
调和映照曲面间的映射所诱导的弹性形变能量被表示成调和能量,使调和能量达到最优的映射被称为是调和映照.对于亏格为0的封闭曲面,调和映射必为共形映射.我们从一个微分同胚出发,运用非线性热流方法,逐步改变映射,使得调和能量逐渐减小,直至达到调和映照.
Hodge分解共形映射的导数是全纯微分,由一对彼此共轭的实调和微分形式构成.Hodge定理断言:流形的每一个de Rham上同调类中有且仅有一个调和微分形式.因此我们计算曲面的上同调群,然后用椭圆型偏微分方程求解调和微分形式,再由调和形式构成全纯微分,通过积分得到共形映射.图5中,亏格为1的曲面的单值化就是由此算出的.
Ricci流Ricci 曲率流由Hamilton发明,用来证明庞加莱猜测.Ricci流的基本思想是将黎曼度量变形,其变形程度正比于当前的Ricci曲率,使得Ricci曲率依随时间演化,其演化规律满足反应-扩散方程,最后曲率处处成为常数.图5中,高亏格曲面的单值化就是由离散曲率流的方法计算出来.目前,不存在其他可以替代的方法.
4 基本任务
下面的计算问题,是计算共形几何中的基本任务.这些问题本质上是相关的:
(i) 共形结构给定一个带有黎曼度量的曲面,计算其内蕴共形结构的各种表示.一种方法是计算阿贝尔微分群,另一种方法是计算标准黎曼度量.
(ii) 共形模完整的共形不变量被称为黎曼面的共形模. 对于给定的黎曼面,计算其共形模.
(iii) 标准黎曼度量拓扑曲面上的所有黎曼度量可以根据共形等价来进行分类.一个基本的定义是单值化定理,每个黎曼度量都共形于一个由常值高斯曲率诱导的黎曼度量.计算单值化度量是计算共形几何中的根本重要问题.
(iv) 共形映射计算给定两个共形等价的曲面之间的共形映射.这可以被归结为计算每个曲面到标准空间上的共形映射,例如球面,平面或者双曲空间上的圆域.
(v) 拟共形映射黎曼面之间的绝大多数微分同胚都不是共形的.它们将无穷小圆映为无穷小椭圆.如果椭圆的长短轴之比有一致的界,那么这个微分同胚被称为拟共形映射. 黎曼面上的拟共形映射的微分由Beltrami系数表示.根据Beltrami系数可以恢复拟共形映射(可相差一个共形映射).如何从Beltrami微分计算拟共形映射是一个基本问题,并有着广泛应用.
5 实际应用
我们在非常广泛的工程和医学领域中展示了计算共形几何的价值,主要原因如下:
(i) 标准域所有的度量曲面都可以被共形地映射为三种标准域之一:球面,平面或双曲圆盘.因此我们可以把三维几何处理问题转化为二维问题. 这极大地简化了算法设计和工程计算.例如某些偏微分方程的解在标准域上有封闭形式,比如单位圆盘上的泊松公式.
(ii) 根据曲率设计度量每种共形结构都有着带有常曲率的标准黎曼度量.这种度量在几何处理问题中具有重要的作用.例如,在双曲度量下,非平凡的闭圈的每个同伦类中具有唯一的闭测地线.进一步,对于给定的曲率,我们可以设计度量,这在几何建模中起到至关重要的作用.
(iii) 一般的几何结构构造其它几何结构,往往要借助共形几何的方法,例如仿射结构,射影结构等等.这些结构在很多工程领域中起到了根本作用.
(iv)构造微分同胚共形映射和拟共形映射可被用于构造曲面间的微分同胚.曲面配准和比较是计算机视觉和医学图像领域的最本质问题.
(v)等温坐标共形结构可被看作是一种特殊的图册,使得所有的局部坐标都是等温坐标.在这种坐标之下,黎曼度量具有最简单的形式.因此,所有的微分算子,例如Laplace-Beltrami算子,在这种坐标下可以被很好地表示.这有助于简化偏微分方程.等温坐标保持局部形状,如图7所示,这在可视化和纹理映射中非常重要.

(a) 圆盘填充(b) 棋盘格 图7 等温坐标
5.1医学图像中的应用
依随核磁共振技术(MRI)和CT断层扫描技术的发展,医学图像被日益广泛地应用于医疗实践之中.例如,利用核磁共振技术,病患的大脑灰质皮层可以被迅速获取下来.通过对灰质皮层曲面形状的分析,医生可以诊断病人脑神经系统存在的隐患,对于病情发展加以监控.这一手段被广泛应用于有关老年痴呆症,帕金森氏综合症等疾病的诊断.人类大脑皮层的形状非常复杂,不同的人之间大脑皮层曲面几何非常不同,即便是同一个人,不同时期的大脑皮层的形状也不相同.如何建立不同大脑皮层曲面间的映射,对不同皮层曲面加以比较,是一个非常具有挑战性的问题.共形几何提供了一种优雅而有效的解决方法.
如图8所示,人的大脑皮层是亏格为零的拓扑球面,可以被共形地映到单位球面上.这样,我们为大脑皮层上的每一点赋予唯一的球面坐标,从而实现精确地定位.另一方面,不同大脑皮层之间的映射可以由球面之间的自同构映射建立.相比于复杂曲面间的映射,球面到自身的映射非常容易建立.

图8 共形脑图 [4]
人的大脑皮层上的沟回具有非常重要的神经生理学的意义.如图9所示,重要的沟回用黄色曲线勾勒出来.中间的沟回在人的胚胎期形成,负责人的基本情感.在建立大脑皮层间的映射时,这些重要沟回需要对齐.我们沿着这些沟回将曲面切开,再共形地将曲面映到平面带圆形孔洞的圆盘.在建立圆盘间映射的时候,我们刻意将圆形孔洞对齐,这样就保证了原来大脑皮层曲面间映射将重要的沟回对齐.
直肠癌是人类的第四号杀手.直肠癌是由直肠息肉经过不断的摩擦而发生癌变转换而来.如果在早期,通过肠镜检查,及时发现直肠息肉,并对较大的息肉进行剪除,直肠癌可以避免.因此,肠镜检查对于中老年人群而言非常重要.但是,传统的肠镜检查需要对病人进行麻醉处理,病人需要承担一定风险,对医生的手工操作具有很高要求,费时费力,对病患具有一定的侵犯性.

图10 基于共形几何的虚拟肠镜[5]
病患的直肠曲面可以由CT断层扫描技术获取,如图10所示.直肠壁曲面有许多皱褶,直肠息肉有可能隐藏在这些皱褶中.传统肠镜方法无法检查皱褶中的息肉,因此具有一定的误诊漏诊率.一个自然的想法在于展平所有直肠曲面的皱褶,从而揭示所有隐藏其中的息肉和潜在病灶.我们利用共形几何的方法,将直肠曲面周期性地映到平面,每一个周期是个长方形.所有直肠曲面的几何信息一目了然.这种虚拟肠镜的方法,病人不需要做麻醉,和病人无肢体接触,不具有侵犯性.无复杂手工操作,简便易行,提高了诊断准确率和效率.目前,这种虚拟肠镜技术已经广泛应用于北美临床诊断实践之中.
5.2机械制造工业中的应用
汽车,轮船,飞机,火车,几乎所有的机械设备都由数控机床加工制造.曲面几何在制造工业中的数字表示形式是所谓的样条曲面.样条曲面由分片有理多项式组成.通常情况下,样条曲面需要二阶光滑可导.比如大家都希望轿车的车体光可鉴人, 并且车体表面的反射图像也是光滑连续的.在几何上,这意味着车壳表面应当曲率连续.数控机床以样条曲面为输入,计算刀具运行的轨迹,力度,速度等等,将金属毛坯加工成光滑的曲面.
设计师利用石膏雕塑出所设计的款式,三维扫描仪可将现实中的曲面数字化,输出稠密的点云.应用三维Delaunay三角剖分的算法,点云可以被转化为多面体曲面.将多面体曲面转换成光滑样条曲面是饶有兴味的问题.传统样条曲面的构造方法是基于仿射几何不变量的.对于拓扑简单的曲面,我们可以只用一个整体的参数域来覆盖全部曲面,并在参数域上构造样条.

图11 曲面的共形参数化
如图11所示,我们将米开朗基罗的大卫王的头像雕塑曲面共形地映射到平面,从而得到曲面的共形参数.图12展示了由这种方法得到的样条曲面.我们在几何复杂的区域,如眼睛,前额处的头发,增加了控制点的密度;在相对平滑的区域,如面颊,前额,控制点相对稀疏.这样,我们能够利用有限的控制点达到对曲面形状最好的刻画.

图12 米开朗基罗的大卫头像的样条曲面[6]
对于曲面具有复杂拓扑的情形,构造全局光滑的样条曲面等价于构造原曲面的仿射结构.根据示性类理论,由于拓扑障碍,全局仿射结构很多时候并不存在.样条曲面上不可避免存在奇异点.在奇异点,曲率不连续,曲面的反射图像在奇异点有可能间断.所以,实际生产中,我们应当尽量减少奇异点的个数,并且将奇异点尽量隐藏在不为人注意的地方.因此出于工程需要,奇异点的位置一般由用户指定.构造曲面带有指定奇异点的仿射结构是相对复杂的问题.我们的解决方案是构造一个特殊的黎曼度量,使得所有的曲率集中在奇异点上面.这个特殊的度量自然地引发一个仿射结构.图13显示了一个样条曲面的实例,其上的奇异点由用户指定.

图13 带有指定奇异点的样条曲面
5.3无线网络方面的应用
无线传感器网络是一个近些年来迅猛发展的方向,它能够协同地实时监测、感知和采集网络覆盖区域中各种环境或监测对象的信息,并对其进行处理,处理后的信息通过无线方式发送给观察者.无线传感器网络由称为“微尘”的微型计算机构成.这些微型计算机通常可以通过自我重组形成网络,彼此通信,并交换有关现实世界的信息.
每个微尘只有有限的计算和存储能力,和有限的电池能量储备,特别是所有的微尘只有局部的信息,只能和直接的邻居通讯.网络中通常没有一个掌握全局信息的中枢机构.消息的传递一般由简单的路由协议实现.如图14所示,左图的网络中每一个节点都是一个微尘,若两个节点之间存在一条边,则它们可以直接通讯.网络中的每一个节点具有唯一的坐标,坐标可以由GPS设备得到的真实坐标,也可以是虚拟坐标.网络中信息的传递多由所谓“贪婪”算法实现.假设网络中一个节点得到了一个消息,这个信息包括其目的地节点的坐标,那么当前网络节点将此信息传递给它的一个邻居,使得邻居到目标节点的距离小于当前节点到目标节点的距离.通常情况下,每一次信息传递都使得当前节点到目标节点的距离减小,如果信息能够顺利传递,最终它会抵达目标节点.

图14 基于几何方法的无线传感器网络路由设计[7]
“贪婪”算法简单实用,但是具有致命的缺陷.如图14(a)所示,假设网络中有一些障碍物,例如水塘,建筑物等,这些障碍物会在网络中产生孔洞,如果孔洞不是凸形状,“贪婪”算法会失败.比如信息传到了某个非凸孔洞边缘的角点,非常有可能角点到目标节点的距离小于其任意邻居到目标节点的距离,从而“贪婪”算法无法将信息进一步传递.利用共形几何的方法,我们将原始网络变形,从而所有的边界都成为圆形,如图14(b)所示.那么,可以证明“贪婪”算法在新的网络中保证会成功.换言之,通过改换网络的黎曼度量,我们可以提高网络的性能和效率.
“贪婪”算法所得到的信息传递路径都是网络中链接起点和终点的最短路径.如图14(b)所示,大量的最短路径会贴着网络的孔洞边缘,因此处于网络孔洞边缘的节点的负担会很繁重,电力消耗会比其它节点更快.我们利用几何中的“覆盖空间”的概念来均衡节点的负担.如图14(c)所示,我们将网络关于它所有的内边界“反演”,这样会增加孔洞的数目,缩小孔洞的总面积.我们可以再次将整个网络关于它新的内边界反演,从而进一步缩小所有孔洞的总面积.这样所得到的网络可以多重覆盖原始的网络,即新的网络是旧网络的“覆盖空间”.信息传递在覆盖空间中由贪婪算法完成.这样,所有节点的负载基本均衡.
5.4电影动漫,数字游戏中的应用
纹理贴图在数字游戏中,所有的三维物体的表示都可以分为两部分:几何和纹理.几何表征了物体的形状,由三维空间中的三角网格(离散曲面)表示;纹理表征了物体的材料,质地,颜色,和光学特性,由二维图像表示.将二维纹理图像贴在三维离散曲面的过程被称为“纹理贴图”.纹理贴图需要将三维曲面映射到平面上.如图15所示,在左图中,三维曲面被共形地映射到平面上,在右图中,纹理图像被这映射“拉回”到三维曲面上面.这样,我们看到大理石雕塑的大卫王的头像.

图15 纹理贴图

图16 计算机模仿艺术家的素描图[8]
非真实感渲染很多时候,人们需用计算机模仿艺术家作画.如图16所示,特殊的计算机渲染算法可以产生铅笔素描的艺术效果.艺术家在素描写生过程中,运笔的走向基本上是沿着明暗色调变化最剧烈的方向,和变化最缓慢的方向.这两个方向彼此垂直,被称为曲面的主曲率方向.在几何上,计算机算法等价于如何在曲面上设计光滑矢量场,同时,矢量场的走向尽量与曲面的主曲率方向场保持一致.根据拓扑障碍理论,一般曲面上不存在处处非零的光滑矢量场,矢量场的零点被称为是奇异点.首先,我们可以构造一个新的黎曼度量,使得所有的曲率集中在零点上,换言之,我们生成零点之外的平直度量.在平直空间生成矢量场相对容易许多.然后我们计算曲面的主曲率方向场,通过几何手段融合一些零点.最后根据光照条件计算曲面的明暗色调,在渲染过程中,矢量的密度正比于色调强度.
表情捕捉在今天的CG电影(计算机生成电影), 表情的建模和生成是最具挑战性的问题之一.人类对于表情极其敏感.根据心理认知理论,人类用于识别表情的大脑区域不同于识别一般形状的区域.因此,对于微妙表情的建模和模拟非常困难.人类所有可能的肢体动作构成一个有限维空间,因为人类只有有限个关节,每个关节只有有限个自由度.但是人类所有可能的表情构成了无穷维空间.因此,表情生成具有根本的难度.
近些年来兴起的表情捕捉技术为表情的建模和生成带来了根本性的突破.基于光波干涉原理的高速三维相机可以实时获取表情的动态变化.如图17所示,目前的技术可以达到每秒上百帧的速度,每帧具有上百万采样点;但是,所有得到的扫描曲面都是相互独立的,曲面之间的映射关系需要被建立起来.我们将每帧曲面共形映射到平面上,在平面像上计算特征点,利用优化方法寻找平面圆盘间的映射,如图18所示.平面像之间的映射建立了三维人脸曲面间的映射.我们用统一的网格基于所得的映射贴到所有的人脸曲面上,如图19所示,这样我们可以追踪人脸上每一点变化的轨迹,从而达到表情自动跟踪的目的.

图17 三维动态相机可以实时捕捉人脸表情的动态变化

图18 动态人脸曲面被共形映射到平面圆盘[9]
图20显示了“虚拟明星”的概念.明星的面部几何和纹理,以及各种动态表情被扫描下来,保存在数据库中.导演根据剧情需要,选择合适的表情,视角,嘴型,以及场景,用计算机合成CG电影.这样,真正的明星不需要出演电影,只需要提供各种标准的表情.或者,真人演员的表情被提取出来,转移到卡通人物脸上,从而用表情捕捉技术取代目前的表情建模和合成,提高表情的逼真度和复杂性.

图19 表情自动跟踪[10]

图20 虚拟明星:明星的面部几何和纹理、动态表情被记录下来,保存在数据库中,导演根据剧情需要选择合适的表情,合成CG电影
5.5虚拟/增强现实中的应用
在虚拟现实和增强现实的应用中,如何将光滑曲面离散化是一个基本问题.在离散化的过程中,我们希望能够保证离散曲面足够好地逼近光滑曲面,例如拓扑一致,位置接近,测地距离收敛,曲率测度收敛.我们提出了一种高效而严谨的方法实现离散化,同时保证曲率测度收敛.通过单值化,我们将曲面共形映到标准空间,然后在标准空间上采样,使得采样密度和曲率成正比,计算Delaunay三角剖分,再拉回到原来曲面.图21显示了这样的一个算例.

图21 曲面采样离散化[11]
另一方面,虚拟现实和增强现实的应用中,需要对几何数据进行压缩,力图保持几何质量的同时增大压缩比.利用单值化定理,我们将曲面映到标准空间,那么面积变化率函数加上平均曲率就可以完全复制原来曲面.图22显示了一个离散曲面简化压缩的实例.

图22 离散曲面简化
6 总结展望
从以上的实例可以看到,共形几何不但具有深邃和谐的美学价值,更具有无可比拟的实用价值.几何知识的广泛传播和深入应用,日益促进了生产力的发展,根本地改变了人类社会的日常生活.我们期待几何的进一步发展将为人类带来更多革命性的变革.
同时,作为一个新兴学科,计算共形几何依然有大量尚未解决的问题,面临许多挑战.这些基本的公开问题,需要用更加深刻的理解以及更加精致和准确的算法去解决.下面这些问题在理论和应用上都有非常重要的意义:
(i) Teichmüller映射给定两个度量曲面和它们之间的映射同伦类,计算唯一的具有最小Beltrami系数模的拟共形映射,即所谓的Teichmüller映射.
(ii) Abel Differential计算不同类型的Abel微分群,尤其是全纯二次微分群.
(iii) 逼近理论尽管已经有了计算共形不变量的算法,但是逼近理论的结果还没有充分的发展. 对于平面区域间的共形映射,不同离散方法的收敛性已经被建立. 而对于曲面间的共形映射,收敛性分析仍然是公开问题.
(iv) 精确性和稳定性双曲几何计算对数值误差非常敏感.提高计算的精确度很具有挑战性.计算几何中的精确算法有望攻克这个难题.
我们希望更多的有志年轻人投身到这一领域之中,在理论和工程领域中大展身手,为科学和实践的发展做出历史性的贡献.
[1]Gu X and Yau S-T. Computational Conformal Geometry [M]. Cambridge: International Press and Higher Education Press, 2007.
[2]Luo F, Gu X and Dai J. Variational Principles for Discrete Surfaces [M]. Cambridge: International Press and Higher Education Press, 2007.
[3]Zeng W, Gu X. Ricci Flow for Shape Analysis and Surface Registration -Theories, Algorithms and Applications [M]. New York: Springer, 2013.
[4]Gu X, Wang Y, Chan T F, Thompson P M and Yau S-T. Genus Zero Surface Conformal Mapping and Its Application to Brain Surface Mapping [J]. IEEE Transaction on Medical Imaging (TMI), 2004, 23(8): 949-958.
[5]Zeng W, Marino J, Gurijala K, Gu X and Kaufman A. Supine and Prone Colon Registration Using Quasi-Conformal Mapping[J]. IEEE Transactions on Visualization and Computer Graphics (IEEE TVCG), 2010, 16(6): 1348-1357.
[6]Gu X, He Y, and Qin H. Manifold Splines[J]. Graphical Models, 2006, 68(3):237-254.
[7]Sarkar R, Yin X, Gao J, and Gu X. Greedy Routing with Guaranteed Delivery Using Ricci Flows[C]. Proc. of the 8th International Symposium on Information Processing in Sensor Networks (IPSN’09), 2009:121-132.
[8]Lai Y, Jin M, Xie X, He Y, Palacios J, Zhang E, Hu S and Gu X. Metric-Driven RoSy Fields Design[J]. IEEE Transaction on Visualization and Computer Graphics (TVCG), 2010, 15(3): 95-108.
[9]Zeng W, Samaras D and Gu X. Ricci Flow for 3D Shape Analysis[J]. IEEE Transaction of Pattern Analysis and Machine Intelligence (PAMI), 2010, 32(4): 662-677.
[10]Zeng X, Wang C-H, Gu X. Higher-order Graph Principles towards Nonrigid Surface Registration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), 2015, 1:1-14.
[11]Li H, Zeng W, Morvan J-M, Chen L, Gu X. Surface Meshing with Curvature Convergence[J]. IEEE Transaction on Visualization and Computer Graphics (TVCG), 2014, 20(6):919-93.
Introduction to Computational Conformal Geometry
GUXian-feng1,LEINa2
(1.Computer Science Department,State University of New York at Stony Brook,Stony Brook NY 11794, USA;2. School of Software, Dalian University of Technology, Dalian Liaoning 116620, China)
Computational Conformal Geometry is an interdisciplinary field between pure mathematics and computer science. This work introduces the fundamental theories, computational algorithms and applications in engineering fields of computational conformal geometry. Basic theoretic concepts include conformal mapping, uniformization, conformal module, quasi-conformal mapping, and moduli space and so on. Major computational algorithms include harmonic mapping, holomorphic differential methods based on Riemann surface theory, surface Ricci curvature flow in geometric analysis. Conformal geometry can be applied in many fields, such as medical imaging, mechanical manufacture, digital media and virtual/augmented reality and so on.
conformal geometry; Riemann surface; uniformization; harmonic map; holomorphic differential; surface Ricci flow
2016-05-10;[修改日期]2016-06-13
国家自然科学基金(11271156)
顾险峰(1970-),男,博士,终身教授,从事计算几何研究.Email:gu@cs.stonybrook.edu
雷娜(1977-),女,博士,教授,从事计算几何研究. Email:nalei@outlook.com
O186
B
1672-1454(2016)03-0001-13
