前馈变量对预测控制可行域的影响分析
2016-10-14张佳罗雄麟许锋许鋆
张佳,罗雄麟,许锋,许鋆
前馈变量对预测控制可行域的影响分析
张佳,罗雄麟,许锋,许鋆
(中国石油大学自动化系,北京 102249)
实际生产过程中,预测控制因其解耦性能和强鲁棒性得以广泛使用。在预测控制的研究中大都忽略控制过程中的干扰作用。对于控制过程中存在的可测且变化规律已知的干扰作用,干扰对输出的影响具有一定的可预见性,可通过在预测控制器中引入前馈的方法加以利用。前馈变量的引入会对系统的控制效果产生影响,如果不先对其影响进行分析而直接求解优化,最终结果不能反映预测控制的实际效果。本文从可行域的角度出发,通过几何表现形式,直观分析前馈变量的引入造成的可行域变化;进一步使用了凸空间的思想,通过求解可行域的顶点集合来确定可行域的大小,进而得出前馈变量对系统可行域的影响效果,通过仿真验证了本文方法的有效性。
过程控制;预测控制;前馈;可行域
引 言
模型预测控制作为一种在工业过程中广泛应用的优化控制算法,由于其约束处理能力、解耦性和强鲁棒性在复杂工业系统中展现了良好的控制性能[1]。近年来对于模型预测控制的研究取得了巨大的发展。
前馈在预测控制中起着非常重要的作用[2]。对于前馈在预测控制中作用的研究,目前应用最广泛的是通过加入干扰观测器来抑制扰动的作用[3-4],此种方法因干扰模型与实际的模型不符,控制效果不能满足要求[5]。其他对干扰的处理是通过辨识或者物理建模获得干扰的模型,采用前馈的方法抑制扰动的作用[6]。
王永宾等[7]通过研究干扰量与输出误差之间的关系,提出一种基于灰预测理论的抗扰动模型预测控制方法。李奇安等[8]把系统的可测干扰作为系统的输入,其中间变量作为系统的多输出变量,提出了多前馈-反馈广义预测控制算法。赵慧荣等[9]基于前馈的方法抑制扰动的作用改善系统的控制效果。包健等[10]提出了一种前馈广义预测控制算法,克服了可测扰动对系统的影响。岳俊红等[11]基于预估补偿思想,提出了改进的可测扰动前馈补偿预测函数控制算法。
以上方法在改进扰动对系统控制效果的影响方面起到了很大的作用。但是这类算法的前提是假设扰动项的存在不会影响系统的可行性,或者是基于系统仍有可行域的前提下的。由于扰动的复杂性和随机性,若不先对扰动对系统造成的影响效果进行判断,给出的优化算法并不能反映系统的实际情况。所以应先对扰动对系统的影响进行分析,再通过改进控制算法,优化系统的控制效果。
对于不可测扰动,因其变化规律未知,无法预测其对系统的影响。但是对于变化规律已知扰动,由于它对输出的影响有一定的可预见性,可以通过分析扰动的模型,预测扰动对系统的影响。干扰对预测控制的影响研究中,张强等[12]曾提出了预测控制前馈-反馈可达性基准,对加入干扰后的系统控制性能进行监控,但此种方法并不直观。何德峰等[13]、史冬琳等[14]研究了有界扰动对系统控制效果的影响。Tran等[15]提出了可匹配前馈控制的广义预测控制算法。
对于变化规律已知的扰动,其变换范围有界,扰动的引入势必对系统的可行域带来影响,通过计算推导系统可行域的变化,可以直观地看出扰动对系统的影响。
本文将从可行域的角度出发,采用映射的思想,通过计算扰动带来的系统可行域的变化,分析扰动对预测控制效果的影响。
1 具有可测扰动控制过程的描述
1.1 不考虑扰动的MIMO系统的状态空间模型
模型预测控制的系统状态空间模型如下
对输出的步预测为


其中,

约束优化的约束条件为

由式(2),约束条件可写为
1.2 考虑扰动的MIMO系统的状态空间模型
考虑存在已知但不可控干扰的对象,若预测控制采用机理建模得到如下线性时不变离散状态空间模型
对输出的步预测为


其中,



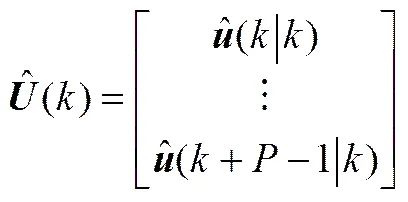
约束优化的约束条件

可写为

根据式(5),约束空间可写为
2 前馈变量影响下系统可行域变化的分析
2.1 预测控制系统可行域的判断
针对预测控制存在输入输出约束条件,分别定义输出约束空间为,输入约束空间为。在实施预测控制过程中,满足,使得的区间为系统的可行域[16]。
根据以上定义,系统是否有可行域问题转化为以下约束空间是否非空问题
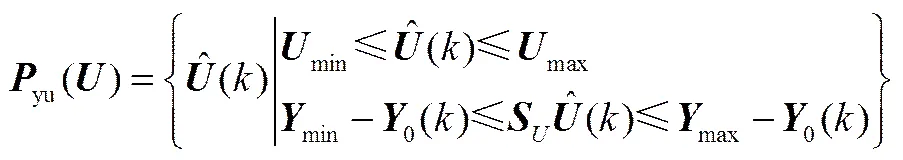
对比式(3)和式(6)可以看出,前馈变量的引入,使得输出约束空间进行了的平移。平移将使得映射空间的大小发生变化,其变化几何表现形式如图1所示。图1(a)为无前馈影响下的预测控制可行域大小,图1(b)为有前馈影响下的可行域的变化,变化部分即为式(3)和式(6)变化的造成初始约束空间的平移。

图1 前馈对预测控制可行域的影响
由此可以看出,由于前馈的影响,系统约束的映射区间进行的平移对系统可行域带来的影响是非常显著的,若平移的方向未知,则前馈导致系统可行域大小变化也是未知的。
若由于前馈的影响,系统的可行域变大了,那么在未考虑扰动影响时采用的优化算法则略显保守;若可行域变小了,则算法过于激进。所以在优化系统前,应先对前馈变量对系统可行域的影响进行分析。
2.2 前馈变量对预测控制可行域影响大小的判断
记



下面给出两个引理,并通过它们求出约束映射空间的顶点。
引理1[17]凸多面体非空的充分必要条件是和,可以分解为

引理2[18]设凸多面体,其中为矩阵,,的秩为,为的极点的充分必要条件是和可以作下列分解


根据以上方法,在控制系统有可行域的情况下,求得凸约束空间的所有顶点坐标,其顶点组合即为的可行域。对于有干扰的预测控制系统,可分别分析有无前馈变量情况下可行域的差异,得出前馈变量对可行域的影响。加入前馈变量后若可行域过小或无可行域的控制系统,可通过放宽系统约束[19-20],使得系统可控或控制效果更优。
3 仿真实例
以经典的Shell石油公司重油分馏塔为例,采用基于过程输入输出数据的辨识方法,获得系统的模型参数[21-23]。考虑中段循环回流负荷为前馈变量。使用上文中前馈变量对预测控制可行域的影响分析,对比是否考虑系统扰动情况下,系统的仿真结果。
选取模型的3个操作变量、3个被控变量、1个扰动变量,各变量含义见表1。模型传递函数矩阵为

其中,传递函数中各变量已经过量纲1化处理,时间常数单位为min,根据香农采样定律[24]采样时间选取为4 min。假设系统初始输出为零。使用Matlab仿真。


表1 Shell模型变量
系统被控目标为

(1)不将系统的扰动考虑进系统模型情况下,对系统进行仿真。结果如图2所示,对应可行域几何示意图如图3所示。

图2 不考虑扰动情况下系统仿真结果

图3 无扰动情况下预测控制的可行域几何示意图
塔顶循环回流负荷是存在且已知的,其对系统控制效果必然产生影响,并且影响是可以预知的。以上仿真结果并不能反映系统真实的控制效果。
(2)将系统的扰动加入到系统模型中,考虑扰动对控制效果的影响。因扰动的存在,使用本文中的方法进行分析,得到约束映射空间为空,系统无可行域。其可行域几何示意图如图4所示。

图4 考虑扰动后系统无可行域的几何示意图
扰动对系统的影响是隐性的,若不对扰动进行观测控制,系统的可行域变化情况未知,其控制效果也不是最优的。
对系统约束进行调整,放宽被控变量的上下限,使得输入输出约束空间有交集,映射空间不为空。将被控变量约束调整为

对系统进行仿真,仿真结果及可行域几何示意图如图5、图6所示。可以看出,前馈变量对系统可行域的影响是十分明显的,变量的引入可导致系统无法找到可行解,以致系统无法运行。不考虑前馈变量下给出的系统输入输出约束过紧,投入到实际过程中系统无法运行。

图6 调整约束后系统可行域几何示意图
4 结 论
本文基于可行域的思想,通过几何表现形式直观地给出了前馈对预测控制效果的影响。在预测系统控制优化过程中,若扰动是规律已知的,则应优先对前馈变量的引入造成的系统可行域变化进行分析,在得出系统的实际控制效果后再对系统进行优化,可令优化结果更准确,更符合实际。
References
[1] 席裕庚, 李德伟, 林姝. 模型预测控制——现状与挑战 [J]. 自动化学报, 2013, 39 (3): 222-236.
XI Y G, LI D W, LIN S. Model predictive control—status and challenges [J]. Acta Automatica Sinica, 2013, 39 (3): 222-236.
[2] CARRASCO D S, GOODWIN G C. Feedforward model predictive control [J]. Annual Reviews in Control, 2011, 35 (2): 199-206.
[3] VALENCIA-PALOMO G, ROSSITER J A, LÓPEZ-ESTRADA F R. Improving the feed-forward compensator in predictive control for setpoint tracking [J]. ISA Transactions, 2014, 53 (3): 755-766.
[4] NÚÑEZ-REYES A, NORMEY-RICO J E, BORDONS C,. A Smith predictive based MPC in a solar air conditioning plant [J]. Journal of Process Control, 2005, 15 (1): 1-10.
[5] ROSSITER J A. Model-based predictive control: a practical approach [J]. Mechanical Engineering, 2003, 10: 68-68.
[6] TOMIZUKA M. Model based prediction, preview and robust controls in motion control systems [J]. International Workshop on Advanced Motion Control, 1996, 1: 1-6.
[7] 王永宾, 许军, 周奇勋. PMSM调速系统新型抗扰动模型预测控制策略 [J]. 科学技术与工程, 2014, 14 (36): 61-66.
WANG Y B, XU J, ZHOU Q X. The improved anti-interference model predictive control strategy for PMSM speed control system [J]. Science Technology and Engineering, 2014, 14 (36): 61-66.
[8] 李奇安, 李平, 于海斌, 等. 串联系统的多前馈-反馈广义预测控制 [J]. 控制与决策, 2002, 17 (4): 402-406.
LI Q A, LI P, YU H B,. Multiple feed-forward and feedback generalized predictive control for cascade system [J]. Control and Decision, 2002, 17 (2): 402-406.
[9] 赵慧荣, 沈炯, 沈德明, 等. 主汽温多模型扰动抑制预测控制方法 [J]. 中国电机工程学报, 2014, 34 (32): 5763-5770.
ZHAO H R, SHEN J, SHEN D M,. Multiple model disturbance rejection predictive control of main steam temperature [J]. Proceedings of the CSEE, 2014, 34 (32): 5763-5770.
[10] 包健, 曾文华. 一种前馈广义预测控制算法的研究及其仿真 [J]. 计算机测量与控制, 2000, 8 (3): 44-46.
BAO J, ZENG W H. Research and simulation for a feed forward generalized predictive control algorithm [J]. Computer Measurement and Control, 2000, 8 (3): 44-46.
[11] 岳俊红, 刘吉臻, 刘向杰, 等. 具有可测扰动典型过程的预测函数控制 [J]. 系统仿真学报, 2007, 19 (16): 3752-3755.
YUE J H, LIU J Z, LIU X J,. Predictive functional control for typical process with measurable disturbance [J]. Journal of System Simulation, 2007, 19 (16): 3752-3755.
[12] 张强, 赵艳, 高曼莉. 可测干扰过程的预测控制性能监控 [J]. 河北科技大学学报, 2010, 31 (4): 352-354.
ZHANG Q, ZHAO Y, GAO M L. Performance monitoring of predictive control process with measured disturbance [J]. Journal of Hebei University of Science and Technology, 2010, 31 (4): 352-354.
[13] 何德峰, 季海波, 郑涛. 持续有界扰动下的非线性∞鲁棒预测控制 [J]. 自动化学报, 2008, 34 (2): 215-219.
HE D F, JI H B, ZHENG T. Nonlinear∞robust predictive control with bounded persistent disturbance [J]. Acta Automatica Sinica, 2008, 34 (2): 215-219.
[14] 史冬琳, 毛志忠. 基于仿射控制输入的输入状态稳定非线性预测控制 [J]. 控制理论与应用, 2010, 27 (10): 1388-1392.
SHI D L, MAO Z Z. Input-to-state stabilizing nonlinear model-predictive-control based on affine control input [J]. Control Theory and Applications, 2010, 27 (10): 1388-1392.
[15] TRAN Q N, ÖZKAN L, BACKX A. Generalized predictive control tuning by controller matching [J]. Journal of Process Control, 2015, 25: 1-18.
[16] 周晓龙. 多变量系统状态约束预测控制及相关研究 [D]. 北京: 中国石油大学, 2013.
ZHOU X L. Model predictive control with state constraints and related problems [D]. Beijing: China University of Petroleum, 2013.
[17] 戴连奎, 李晓东. 稳态约束优化控制可行性分析的新方法 [J]. 控制理论与应用, 1998, 15 (6): 925-928.
DAI L K, LI X D. A new method for feasibility analysis of optimal control of steady state constraints [J]. Control Theory and Application, 1998, 15 (6): 925-928.
[18] 陈宝林. 最优化理论与方法 [M]. 北京: 清华大学出版社, 1989.
CHEN B L. Optimization Theory and Slgorithm [M]. Beijing: Tsinghua University Press, 1989.
[19] 张惜岭. 多变量控制约束映射与约束预测控制相关问题研究 [D]. 北京: 中国石油大学, 2011.
ZHANG X L. Multivariable control constraint mapping and related problems of constrained model predictive control [D]. Beijing: China University of Petroleum, 2011.
[20] 杨柳, 袁景淇. 压水堆蒸汽发生器水位的前馈模型预测控制 [J]. 控制工程, 2008, 15 (3): 250-252.
YANG L, YUAN J Q. Model predictive controller with feed forward compensation for steam generator in PWR [J]. Control Engineering of China, 2008, 15 (3): 250-252.
[21] 丁锋. 系统辨识新论 [M]. 北京: 科学出版社, 2013.
DING F. A New System Identification [M]. Beijing: Science Press, 2013.
[22] 丁锋. 系统辨识: 辨识方法性能分析 [M]. 北京: 科学出版社, 2014.
DING F. System Identification: Performance Analysis of Identification Methods [M]. Beijing: Science Press, 2014.
[23] 丁锋. 系统辨识(6): 多新息辨识理论与方法 [J]. 南京信息工程大学学报: 自然科学版, 2012, 4 (1): 1-28.
DING F. System identification (part F): Multi-innovation identification theory and methods [J]. Journal of Nanjing University of Information Science and Technology, 2012, 4 (1): 1-28.
[24] 赵明生, 李爱梅. 预测控制参数的选取原则和计算方法 [J]. 计算技术与自动化, 2005, 24 (4): 88-90.
ZHAO M S, LI A M. Choose principia and calculate method of model predictive control parameters [J]. Computing Technology and Automation, 2005, 24 (4): 88-90.
Influence of feed forward variables on feasible region of model predictive control
ZHANG Jia, LUO Xionglin, XU Feng, XU Jun
(Department of Automation, China University of Petroleum, Beijing 102249, China)
The model predictive control is widely used in real process because of its decoupling and strong robustness. In the past studies, the effects of disturbances on model predictive control were mostly ignored. For the measurable disturbances whose dynamic rules are known, the influence of measurable disturbances on controlled variables can be predicted, and thus the measurable disturbances can be used as feed forward variables in model predictive control. The introduction of feed forward variables will affect the control performance of the system. The result solving directly under no analysis cannot reflect the actual effect of model predictive control. From the viewpoint of feasible region, this paper studies the feasible region changes caused by feed forward variables through the geometric forms. The convex space method is used to determine the size of the feasible region by solving the feasible region of the vertex set and obtain the effects of feed forward variables on the feasible region. The simulations verify the validity of the method in this paper.
process control; model predictive control; feed forward; feasible region
supported by the National Basic Research Program of China (2012CB720500).
date: 2016-01-08.
Prof. LUO Xionglin, luoxl@cup.edu.cn
TP 273
A
0438—1157(2016)09—3776—08
10.11949/j.issn.0438-1157.20160036
国家重点基础研究发展计划项目(2012CB720500)。
2016-01-08收到初稿,2016-06-02收到修改稿。
联系人:罗雄麟。第一作者:张佳(1988—),男,硕士研究生。
