多尺度熵在棒束通道气液两相流压差信号分析中的应用
2016-10-14周云龙尹洪梅丁会晓
周云龙,尹洪梅,丁会晓
多尺度熵在棒束通道气液两相流压差信号分析中的应用
周云龙,尹洪梅,丁会晓
(东北电力大学能源与动力工程学院,吉林省 吉林市 132012)
棒束通道气液两相流的压差信号是非线性的,多尺度熵法在分析非线性信号方面效果较好。运用多尺度熵对压差信号进行分析,在7×7棒束通道的气液两相流实验台上采集压差信号,针对 104种流动条件4种流型的压差时间序列分析其多尺度熵特征。研究发现:小尺度(前8个)下的多尺度熵率可以准确区分棒束通道4种流型;大尺度下的样本熵变化趋势可以揭示4种流型的动力学特性。
气液两相流;多尺度;样本熵;流型识别;棒束通道;算法
引 言
棒束通道气液两相流动在各种工业设备中广泛存在,尤其在核能领域的压水堆、沸水堆冷却剂丧失事故和余热排出系统丧失事故中较为常见[1]。两相流流型对管道设备传热和流动有着极其重要的影响。目前学者们对气液两相流动的流型及动力学特性研究主要集中在水平管、矩形小通道、蛇形通道等[2-4],对棒束通道两相流流型的识别方法和动力学特性揭示的研究还较少。棒束通道几何结构特殊,不能直接应用普通通道结论。因此对棒束通道两相流动的研究是两相流研究的热点和重点。
压力波动信号包含大量的流动信息[5],两相流动过程具有强烈的非线性特性,因此用非线性分析法研究压差波动信号得到了广泛应用[6-11]。
熵在表征系统非线性特性发面取得了较好的成果[12-13],度量了系统的复杂性和不规则性。自1991年近似熵[14]提出后,已广泛应用于各领域。Richman等[15]提出了样本熵,克服了近似熵对数据长度敏感的问题;庄建军等[16]用样本熵分析生理信号,表明样本熵在分析复杂信号能力上优于近似熵,但存在单一尺度不能完全揭示信号复杂性的问题。Costa等[17]改进了样本熵并提出了多尺度熵理论,在心率变异性分析中,发现多尺度熵可以解决单尺度样本熵不能区分不同病症的问题。郑桂波等[18]将多尺度熵应用于垂直上升管的电导波动信号中,发现小尺度下样本熵的变化速率能很好地区分3种典型流型。Zhou等[19]对3×3沸腾状态下棒束通道的压差信号进行多尺度熵分析,发现前多尺度熵可以区分4种流型,并能揭示流型动力学信息。7×7棒束通道4种气液两相流流型的流动特性有很大区别,根据以往的特征提取结合人工神经网络的方法,识别效果常依赖网络参数的选择;而单尺度熵在4种流型识别上存在特征交叉现象,造成流型辨识困难,本文根据4种流型的流动特点采用多尺度熵分析法对其非线性压差信号进行分析,并与已有文献的/分层分析进行对比,以期为流型定量识别提供新思路。
1 多尺度熵算法
多尺度熵是在样本熵[15]基础上,描述时间序列在不同时间尺度上的无规则程度。多尺度熵(MSE)具体算法如下[20]。
(1)给定一维离散时间序列{(),=1,2,…,},对时间序列进行粗-断点(coarse-graining)变换,得到新的时间序列
(2)将得到的长度为=/的时间序列,按顺序组成一组维矢量。
(3)计算()与()之间的对应元素中差值最大的距离[()-()],并对每一个值进行计算。
(4)给定阈值,对于每一个统计()与()间的对应元素差值最大的距离小于的个数,计算此个数占距离总数m的比值,即
(5)对所有点求均值,记作,m(),即
(6)增加维数至1,重复步骤(2)~步骤(5),得到,m+1()。
(7)计算样本熵
(8)计算粗粒化后每个尺度对应的时间序列的样本熵值,即为多尺度熵
多尺度熵并不等同于粗粒化后分别计算样本熵。取2,容限取原始时间序列的标准差(SD)的0.1~0.25倍,正因如此多尺度熵能够在多尺度上反映系统复杂性。
2 多尺度熵方法评价
本文选取Logistic、Henon、正弦、正弦+噪声、Lorenz 及Lorenz+噪声6种典型信号验证多尺度熵理论应用的广泛性[21]。
① 正弦信号3sin(),采样间隔为 π/500。
② 正弦+噪声
3sin()1
其中,1是高斯白噪声序列,是随机成分占的比例,取= 0.2。
③ Lorenz 方程
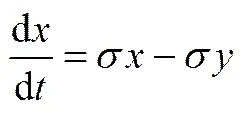

其中,=10,=28,=38,初始条件=10,=1,=0,采用四阶Runge-Kutta方法迭代,取变量为仿真序列。
④ Lorenz+噪声,在③中所得变量+30 dB噪声。
⑤ Logistic映射
其中,=3.9,初始条件为0=0.4,取变量为仿真序列。
⑥ Henon映射

y+1=bx(8)
其中,=1.4,=0.3,0=0,0=0。
各典型信号多尺度熵变化情况如图1所示,与文献[18]验证吻合:白噪声样本熵呈下降趋势;正弦信号加噪前后样本熵变化一致,前9个尺度缓慢增加,第10个尺度之后基本保持在较低熵值不变,说明其序列具有周期性;Lorenz序列加噪前后样本熵变化一致,熵值先增加后降低,第12个尺度后熵值出现振荡,说明Lorenz序列复杂度较高;Henon和Logistic序列的变化趋势相似,仅从单尺度样本熵无法区分两个序列,而从第3到第6个尺度上可以看出两个序列样本熵值差异明显,这表明多尺度熵比单一尺度样本熵具有优越性;Henon、Logistic和Lorenz 3个混沌时间序列,多尺度熵变化上的差异表明多尺度熵可以研究混沌时间序列的确定性;白噪声和正弦信号,多尺度熵变化趋势的不同表明多尺度样本熵可以有效区分不同时间序列的复杂性;而且从Lorenz序列和正弦信号加噪前后多尺度样本熵基本保持一致可以看出,多尺度样本熵法具有很好的抗噪能力。
图2为白噪声在不同序列长度下的样本熵,不同长度序列的样本熵变化趋势相近差异很小,说明多尺度熵法对数据长度不敏感,有很好的鲁棒性。
3 压差信号获取
实验是在棒束通道气液两相流实验台上完成的,具体流程见文献[22]。实验段为7×7的垂直棒束实验段,实验段外壳采用厚为10 mm的透明有机玻璃板,围成横截面为150 mm×150 mm的正方形通道。实验段总长为1120 mm,分别在距离入口处200、290、480、670、860、950 mm处设置6个测压点,整个实验段透明光滑可视。实验流程及实验段结构如图3、图4所示。实验以空气和水作为工质,二者混合后进入实验段,通过差压变送器和数据采集仪采集压差信号,用高速摄影仪拍摄流型。压力信号采集选择压力传感器为Rosemount 3051S 电容式压力传感器,测量精度0.075%,响应时间为100 毫秒/次。压差信号采集选择Rosemount 3051S 电容式差压变送器,其测量精度为0.05%,响应时间为100 毫秒/次。数据采集选择IDTS–4516U 型16 通道采集仪。采用瑞士公司研发的高速摄像系统,其最大分辨率为 1536×1024,最大帧频达到10000 帧/秒。实验中压差动态数据的采集频率为1000 Hz,数据采集20 s,选取流动稳定后的6 s内数据作为采样点。实验共采集了104种流动条件,得到了泡状流、泡状-搅混流、搅混流、环状流4种流型,由于实验条件所限得到的主要流型是泡状流和搅混流,图5是实验采集的4种压差信号。
4 结果分析
对4种压差信号进行多尺度熵分析,维数取2,取原始时间序列的标准差的0.12倍,考虑运算速度和信号完整性,序列长度取6000。
4.1 流型识别
w=0.502 m3·h-1和w=6 m3·h-1时4种流型压差信号的多尺度熵如图6、图7所示,由图可以看出前8个尺度的多尺度熵值呈线性增长且不同流型的熵值增长程度不同。将前8个尺度熵的增长率用最小二乘法进行线性拟合得到其斜率,定义为多尺度熵率。依据不同流型的多尺度熵率不同来识别流型。
图8显示了104种流动条件下的多尺度熵率分布情况:泡状流为0.1~0.16;泡状-搅混流为0.08~0.1;搅混流为0.05~0.08;环状流在0.08以下。104种流动条件中,整体识别率达到97.11%,只有3个泡状-搅混流不在划分区域,因为泡状-搅混流属于过渡流型,特征不明显不易区分。对于主要流型泡状流和搅混流识别率可以达到100%。
4.2 动力学特性分析
从图6w=0.502 m3·h-1和图7w=6 m3·h-1时的多尺度熵可以看出4种流型在前8个尺度上的熵值变化趋势相似,随着尺度增加熵值变化差异增加。总体来看熵值大小:泡状流>泡状-搅混流>搅混流>环状流。说明泡状流的信号最复杂,搅混流的信号次之,泡状-搅混流信号位于泡状流和搅混流之间,环状流的信号相对复杂度最低。
从各个尺度细节上可以发现:前8个尺度上熵的增长速率存在明显差异,泡状流的增长速率最快,其次是泡状-搅混流、搅混流、环状流;从第9个尺度以后,泡状流增长平缓,随着尺度增加表现为随机变化,最终趋于平稳;泡状-搅混流作为过渡流型变化趋势位于泡状流和搅混流之间,随着尺度增加熵值增加趋近泡状流;搅混流从第9个尺度后增长平稳,偶有降低趋势并伴有小幅振荡;环状流的熵值最低,且增长相对平缓,在13个尺度后熵值趋于稳定,没有出现明显的振荡和降低现象。不同流型的多尺度熵的变化特征可以反映不同流型流动特性。
(1)泡状流 气泡的运动非常复杂,在棒束通道内的主体是液相,离散的小气泡在液相中随机分布,大多数气泡在子通道内随液相向上运动,极少量气泡会在相邻通道内漂移,此时气泡直径较小,基本都在2~6 mm之间,气泡分布比较离散,未充满子通道。此信号类似随机信号,故其熵值最高。
(2)泡状-搅混流 小气泡不断向相邻通道移动聚集,气泡增大到一定尺寸变形为椭圆形或长条形,但由于子通道较狭窄,棒束对聚合气泡的扰动及分割十分强烈,使得没有出现与圆管通道中相同的弹状流,而是直接过渡到搅混流,熵值小于泡状流。
(3)搅混流 气泡在棒束内发生聚合和扭曲,扰动变得十分剧烈,聚合气泡横跨1~2个子通道,状态十分不稳定,很快发生破裂。气泡破裂后产生很多不规则气泡,掺杂分布在液相中,气泡的直径大于起初的气泡,但还未充满整个通道。这种流型的一个显著的特征是振荡,随着向上运动的大气泡的拖拽,使液体产生交替的上下运动,且在较广的工况范围内存在时间较长。当搅混流流型出现时,气相和液相在棒束通道内受到强烈的扰动,对构成通道的棒束和套管内壁形成强烈的冲刷。振荡的随机流动现象没有泡状流明显,所以其熵值比泡状流低。
(4)环状流气相所占体积比例越来越大,已远大于液相体积。通道内的块状液流被击碎,气泡团聚并沿棒束形成连续的气柱,液相在子通道内以液膜的形式向上流动,气柱内以液滴的形式夹带大量的液体在两相交界面形成锯齿状交界面。由于液相体积减少,通道内流体受重力影响减小,上下振荡幅度慢慢减小。此信号具有一定周期性,所以其熵值比较低且相对平稳。
4.3 方法比较
小波分析结合(rescaled range analysis,重标极差分析法)分形分析[23-25]表明压差信号具有分形特性并揭示了气液两相流动的动力学特性:将多尺度熵分析方法与其进行对比,采用7小波对压差信号进行6层分解,图9是4种流型在各尺度下的分析结果,细节信号1呈一个明显线性关系,近似信号6和细节信号26不同于细节信号1,具有一个突变点、两个明显线性关系;1尺度(1)下的细节信号具有单分形特性,2<0.5具有反持久性;2~6尺度(26)下的细节信号和7(6)尺度下的近似信号具有双分形特性,1>0.5具有正持久性,2<0.5具有反持久性。
各尺度下的Hurst指数分布如图10所示,除了细节尺度1(1)外各尺度上较大Hurst指数均接近1,代表气液两相流的宏观稳定性;在4、5尺度较小Hurst指数中,泡状流最小,搅混流和环状流接近0.5;其他尺度上Hurst无明显类似变化规律。综上,小波分析结合/分形分析可以揭示各尺度上流型的动力学特性,但是不能有效地对流型进行分类。
5 结 论
(1)运用多尺度熵对压差信号进行分析,依据多尺度熵率可以对流型进行分类,对泡状流、泡状-搅混流、搅混流、环状流的整体辨识率达到97.11%,对主要流型泡状流和搅混流的识别率达到100%。
(2)不同流型的多尺度熵在各尺度上的变化趋势差异较大,所以多尺度熵分析法能够从细节尺度上揭示气液两相流动动力学特性,可以作为非线性分析的有力工具。
(3)将多尺度熵分析与另一种混沌时间序列分析方法/分析法进行对比,发现多尺度熵分析方法在流型辨识方面更具有优越性。
(4)多尺度熵分析法不仅能够从宏观上作为流型识别的指示器,而且能够从微观上揭示棒束通道的气液两相流的动力学特性。
符 号 说 明

MSE——多尺度熵 R——极差 S——标准差 x(i)——压差波动信号 下角标 g——气相 w——液相
References
[1] CHEN S W, LIU Y, HIBIKI T,. Experimental study of air-water two-phase flow in an 8× 8 rod bundle under pool condition for one-dimensional drift-flux analysis[J]. International Journal of Heat and Fluid Flow, 2012, 33(1): 168-181.
[2] 李洪伟, 周云龙, 宋倩, 等. 水平气液两相流流型图像信息递归特征分析[J]. 化工学报, 2010, 61(6): 1431-1436.
LI H W, ZHOU Y L, SONG Q,. Recursive feature of gas-liquid two-phase flow pattern based on information entropy series of flow image[J]. CIESC Journal, 2010, 61(6): 1431-1436.
[3] 周云龙, 王红波. 矩形小通道内气液两相流垂直向上流动特性[J]. 化工学报, 2011, 62(5): 1226-1232.
ZHOU Y L, WANG H B. Flow characteristics of gas-liquid two-phase flow in small vertical rectangular channel[J]. CIESC Journal, 2011, 62(5): 1226-1232.
[4] 周云龙, 孙振国. 蛇形微通道气液两相流动特性[J]. 化工学报, 2015, 66 (11): 4350-4358.
ZHOU Y L, SUN Z G. Gas-liquid flow characteristics in serpentine microchannels[J]. CIESC Journal, 2015, 66(11): 4350-4358.
[5] 白博峰, 郭烈锦, 陈学俊. 空气-水两相流压差波动研究[J]. 中国电机工程学报, 2002, 22(3): 22-26.
BAI B F, GUO L J, CHEN X J. Fluctuating differential pressure for air-water two-phase flow[J]. Proceedings of the CSEE, 2002, 22(3): 22-26.
[6] 李洪伟, 周云龙, 杨悦, 等. 氮气-水两相流流型平滑 Wigner 三谱切片时频特征[J]. 化工学报, 2013, 64(10): 3571-3580.
LI H W, ZHOU Y L, YANG Y,. Time-frequency characteristics of smoothed Wigner tri-spectrum slices of nitrogen-water two-phase flow patterns[J]. CIESC Journal, 2013, 64(10): 3571-3580.
[7] 樊春玲, 金宁德, 陈秀霆, 等. 两相流流动结构多尺度复杂熵因果关系平面特征[J]. 化工学报, 2015, 66(4): 1301-1309.
FAN C L, JIN N D, CHEN X T,. Two-phase flow structure in multi-scale complexity entropy causality plane[J]. CIESC Journal, 2015, 66(4): 1301-1309.
[8] 周云龙, 顾杨杨. 基于独立分量分析和 RBF 神经网络的气液两相流流型识别[J]. 化工学报, 2012, 63(3): 796-799.
ZHOU Y L, GU Y Y. Flow regime identification of gas/liquid two-phase flow based ICA and RBF neural networks[J]. CIESC Journal, 2012, 63(3): 796-799.
[9] 金宁德, 苗龄予, 李伟波. 气液两相流差压测量波动信号的符号序列统计分析[J]. 化工学报, 2007, 58(2): 327-334.
JIN N D, MIAO L Y, LI W B. Symbolic sequence statistical analysis of differential pressure measurement fluctuating signal of gas/liquid two-phase flow[J]. CIESC Journal, 2007, 58(2): 327-334.
[10] 赵凯, 仲兆平, 王肖祎, 等. 基于HHT 法的流化床内生物质和石英砂双组分颗粒压差脉动信号分析[J]. 化工学报, 2015, 66(4): 1282-1289.
ZHAO K, ZHONG Z P, WANG X Y,. Pressure fluctuation signal analysis of two-component biomass and quartz sand particles based on Hilbert-Huang transform in fluidized-bed[J]. CIESC Journal, 2015, 66(4): 1282-1289.
[11] 金宁德, 陈万鹏.混沌递归分析在油水两相流流型识别中的应用[J]. 化工学报, 2006, 57(2): 274-280.
JIN N D, CHEN W P. Application of chaotic recurrence analysis for identification of oil/water two-phase flow patterns[J]. Journal of Chemical Industry and Engineering(China), 2006, 57(2): 274-280.
[12] LETZEL H M, SCHOUTEN J C, KRISHNA R,. Characterization of regimes and regime transitions in bubble columns by chaos analysis of pressure signals[J]. Chemical Engineering Science, 1997, 52(24): 4447-4459.
[13] LIU M, HU Z. Studies on the hydrodynamics of chaotic bubbling in a gas‐liquid bubble column with a single nozzle[J]. Chemical Engineering & Technology, 2004, 27(5): 537-547.
[14] PINCUS S M. Approximate entropy as a measure of system complexity[J]. Proceedings of the National Academy of Sciences, 1991, 88(6): 2297-2301.
[15] RICHMAN J S, MOORMAN J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000, 278(6): H2039-H2049.
[16] 庄建军, 宁新宝, 邹鸣, 等. 两种熵测度在量化射击运动员短时心率变异性信号复杂度上的一致性[J]. 物理学报, 2008, 57(5): 2805-2811.
ZHUANG J J, NING X B, ZHOU M,. Agreement of two entropy-based measures on quantifying the complexity of short-term heart rate variability signals from professional shooters[J]. Acta Physica Sinica, 2008, 57(5): 2805-2811.
[17] COSTA M, GOLDBERGER A L, PENG C K. Multiscale entropy analysis of complex physiologic time series[J]. Physical Review Letters, 2002, 89(6): 068102.
[18] 郑桂波, 金宁德. 两相流流型多尺度熵及动力学特性分析[J].物理学报, 2009, 58(7): 4485-4492.
ZHENG G B, JIN N D. Multiscale entropy and dynamic characteristics of two-phase flow patterns[J]. Physical Review Letters, 2009, 58(7): 4485-4492.
[19] ZHOU Y L, HOU Y D, LI H W,. Flow pattern map and multi-scale entropy analysis in 3× 3 rod bundle channel[J]. Annals of Nuclear Energy, 2015, 80: 144-150.
[20] 许小可. 基于非线性分析的海杂波处理与目标检测 [D]. 大连:大连海事大学, 2008.
XIU X K. Sea clutter processing and target detecting based on nonlinear analysis[J].Dalian: Dalian Maritime University, 2008.
[21] 王改云, 马姝靓. 典型混沌系统的Matlab仿真实现[J].中国科技信息, 2008, (3): 252-253.
WANG G Y, MA S L. The simulation reality of typical chaotic systems with Matlab[J]. China Science and Technology Information, 2008, (3): 252-253.
[22] 周云龙, 丁会晓, 杨宁. 棒束通道内气液两相流动摩擦阻力实验研究[C]//中国工程热物理学会多相流学术会议论文集.南京: 2015: 6.
ZHOU Y L, DING H X, YANG N. Experimental study on frictional resistance of gas liquid two-phase flow in rod bundle channel [C]//Chinese Society of Engineering Thermophysics Multiphase Flow Academic Conference Proceedings. Nanjing: 2015: 6.
[23] 秦子明, 李丰泉. 管束间压差波动信号的混沌特性研究[J].东北电力大学学报, 2010, 30(6): 15-19.
QIN Z M, LI F Q. Chaotic characteristics analysis of differential pressure fluctuating signal across tube bundles[J]. Journal of Northeast Dianli University, 2010, 30(6): 15-19.
[24] 孙斌, 许明飞, 段晓松. 水平管内气液两相泡状流的多尺度分形分析[J].中国电机工程学报, 2011, 31(14): 77-83.
SUN B, XU M F, DUAN X S. Multi-scale fractal characteristic analysis of gas-liquid two-phase bubbly flow in horizontal pipe[J]. Proceedings of the CSEE, 2011, 31(14): 77-83.
[25] 陈万鹏. 两相流流型识别方法研究[D]. 天津: 天津大学, 2006.
CHEN W P. Study on the identification of two-phase flow patterns[D].Tianjin: Tianjin University, 2006.
Application of multi-scale entropy in analyzing pressure difference signals of gas-liquid two-phase flow in rod bundled channel
ZHOU Yunlong, YIN Hongmei, DING Huixiao
(School of Energy Resource and Dynamic Engineering, Northeast Dianli University, Jilin 132012, Jilin, China)
Due to non-linearity of pressure difference signals of gas-liquid two-phase flow in rod bundled channel and capability of multi-scale entropy analysis in charactering complex signals, multi-scale entropy analysis was used to study time series of pressure difference signals of gas-liquid two-phase flow in the 7×7 rod bundled channel under 104 different flow conditions. Results showed that the change rate of multi-scale entropy in small scales (no more than 8) could accurately distinguish four flow regimes in the rod bundled channel whereas the trending of large scale sample entropy could disclose dynamic characteristics of each flow regime. Therefore, compared to chaotic time series analysis of R/S method, the multi-scale entropy analysis method could reveal the dynamic characteristics and also accurately distinguish four flow regimes of gas-liquid two-phase flow in the rod bundled channel.
gas-liquid two-phase flow; multi-scale; sample entropy; flow pattern recognition; rod bundle; algorithm
TL 334
10.11949/j.issn.0438-1157.20160334
date: 2016-03-23.
YIN Hongmei, yinhongmeiwell@163.com
A
0438—1157(2016)09—3625—08
2016-03-23收到初稿,2016-06-03收到修改稿。
联系人:尹洪梅。第一作者:周云龙(1960—),男,教授。
