一种基于改进GPR和Bagging的短期风电功率组合预测方法

张颖超，郭晓杰，邓 华



一种基于改进GPR和Bagging的短期风电功率组合预测方法

张颖超1,2，郭晓杰1，邓 华1,2

(1.南京信息工程大学信息与控制学院，江苏 南京 210044；2.南京信息工程大学气象灾害预报预警与评估协同创新中心，江苏 南京 210044)

为提高短期风电功率的预测精度并对功率预测的不确定性进行量化，提出了基于高斯过程回归(Gaussian Process Regression，GPR)和Bootstrap Aggregation (Bagging)的组合预测方法。针对GPR的不稳定性和计算量大的特点，引入了Bagging和训练数据完全条件独立下的近似方法(Fully Independent Training Conditional Approximation，FITC)。同时，在贝叶斯决策 (Bayesian Committee Machine, BCM)的基础上，提出了一种新的权重组合策略。实验表明，基于Bagging和FITC的GPR方法在稳定性、预测精度和训练时间的消耗上都优于传统的GPR方法。在风电功率预测中，改进的GPR可以给出较准确的置信区间，且与极限学习机、最小二乘支持向量机相比较，该方法的预测精度也有明显提高。

GPR；Bagging；风电功率预测；不确定性量化；BCM

0 引言

根据世界风能协会统计，截止到2015年2月，中国、美国、德国的风电装机容量分别达到了114.76 GW、65.88 GW和40.47 GW。风能作为清洁可再生能源，在世界范围内已经得到了广泛的利用。但风的间歇性和波动性，给风能有效、安全的利用带来了极大的挑战，而准确的风电功率预测，可以为风资源并网发电、安全调度、市场竞价等提供重要的参考[1]。随着风力发电的快速发展，单一的短期风电功率预测方法的研究已经较成熟，如高斯过程回归[2]、神经网络[3]、支持向量机[4-5]等，由于单个模型无法全面地解释风力发电整个过程的变化，风电功率预测方法逐渐转向对组合预测方法的研究[1]。组合预测方法可以分摊单个模型的误差，提高预测精度。文献[1,6]提出了两种中尺度数值天气预报(Numerical Weather Prediction，NWP)的组合方式，即同一个NWP模式不同变量的组合和不同的NWP模式间的组合，以达到模式间的互补；文献[7]将NWP和GPR组合起来预测短期风电功率，预测精度较神经网络有明显的提高；文献[8]将模糊信息粒化和最小二乘支持向量机联合建模，对风电功率的波动趋势和波动范围进行研究，可有效地预测风电功率的波动范围。同时，由于风资源的波动性以及风机自身运行的特点，风速对应的功率随机分布在一个范围内，而非单一的值。因此，为辅助调度决策[1]，对功率预测的不确定性进行量化也是研究重点之一。为量化预测功率的不确定性，文献[9]提出了基于极限学习机和Bootstrap的概率预测；文献[10]提出了实时风速和预报风速联合条件下的离散预报误差概率模型，可以预测风速以及风电功率变化的概率分布。

上述方法旨在通过组合方法提高预测精度或者通过概率分布对预测的不确定性进行量化，但未同时将功率预测精度的提高和预测不确定性的量化有效地结合起来。

基于此，本文将改进的GPR应用于短期风电功率预测中。针对GPR计算量大的缺点，引入FITC近似计算方法，即FITC-GPR，以减少GPR处理大量数据所消耗的时间。同时，为降低FITC-GPR的不稳定性，提高预测精度，引入了Bagging方法，用于对FITC-GPR的组合。本文还提出了一种新的模型组合策略BFITC-GPR (FITC-GPR weighted by improved BCM)，并与均值法MFITC-GPR (FITC-GPR weighted by means)进行比较，结果表明，该方法组合后的模型，在稳定性和预测精度方面都有明显的提高。最后，将BFITC-GPR应用到短期风电功率预测中，实验证明，针对预测功率的不确定性，BFITC-GPR可以给出较准确的量化，与极限学习基(ELM)和最小二乘支持向量机(LSSVM)相比较，该方法的预测精度也有明显提高。

1 高斯过程回归

1.1高斯过程简介

高斯过程(Gaussian Process, GP)是一个随机变量的集合，该集合中任意有限个随机变量具有联合高斯分布的特征，其性质可由均值函数和协方差函数确定[11]，即

(3)

1.2 使用FITC减少GPR的计算量

(8)

(9)

2 Bagging和FITC-GPR的组合

2.1 Bagging简介

Bagging[15]是机器学习中的一种模型聚合算法，它先通过Bootstrap方法对训练样本进行重新抽样，然后在新的样本集合上分别训练模型，最后通过均值法或权重法将新模型的预测值组合起来。GP属于不稳定的模型[11]，而Bagging方法尤其适合对不稳定的模型进行聚合[15]。

Bagging中模型的组合方法主要有均值法和权重法。均值法是对个FITC-GPR模型的预测分布求平均，即MFITC-GPR，而权重法是根据每个模型的预测能力，为每个模型赋予不同的权重。根据预测的不确定性，本文在BCM[16]的基础上，提出了一种新的权重组合策略，对应的模型为BFITC-GPR。新的组合方法基于式(11)的规则。

(12)

2.2 BFITC-GPR预测方法

BFITC-GPR方法包括训练和测试两个阶段。训练阶段，先通过Bootstrap对训练样本进行次重抽样，产生个新的训练集，再使用FITC-GPR，分别在个训练样本上进行训练，产生个新的模型。测试阶段，先将测试数据输入个新的模型中，得到个不同的预测均值和方差，再根据式(14)、式(15)提出的模型组合策略，分别对均值和方差进行组合，产生最终的预测分布，即均值和方差。BFITC-GPR方法的预测流程如图1所示。

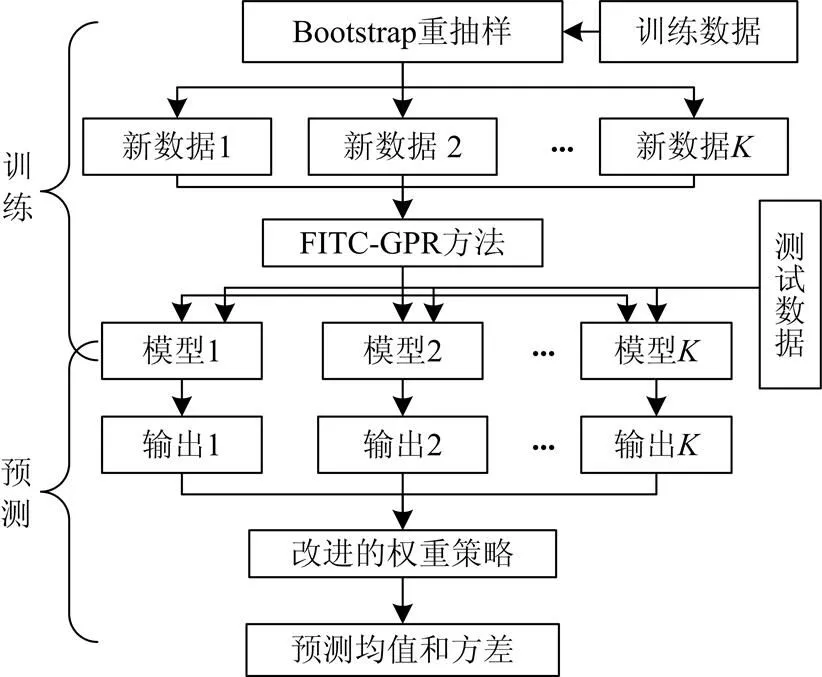
图1 BFITC-GPR方法预测流程图

BFITC-GPR方法结合了FITC-GPR和Bagging的优点。由式(12)知，FITC-GPR的后验分布即为预测值的概率分布，其均值为预测值，方差为对预测值的不确定性的量化。同时，针对FITC-GPR的不稳定性，引入Bagging方法。Bagging可分摊单个FITC-GPR方法的误差，减少偏差，从而提高模型的预测精度。本文将BFITC-GPR方法应用到了短期风电功率预测中，并在下文中通过实验验证该方法的有效性。

3 算法验证及案例分析

实验数据来源于上海某风电场2014年全年数据，包括风机的实际发电功率和风机监测系统采集的风速、风向数据，时间分辨率为15 min，以及2014年全年NWP预报的风速和风向，时间分辨率为15 min。其中，研究风机的切入风速为3 m/s，额定风速为12 m/s，切出风速为25 m/s，额定功率2 MW，扫风面积6 793。本文通过均方根误差(Root Mean Square，RMSE)、绝对平均误差(Mean Absolute Error，MAE)来评价算法的性能[17]，其中，RMSE用来衡量误差的分散程度，MAE用来评价预测误差的平均幅度。

3.1 BFITC-GPR和传统GPR方法对比

文中Bagging的重抽样次数是通过对同一组数据取不同抽样次数时，比较BFITC-GPR预测的来确定的。图2为抽样次数从1取到100时，BFITC-GPR预测值的RMSE。由图2可知，当重抽样次数大于10次以后，虽然测试样本的RMSE仍然在波动，但波动的范围趋于稳定。因此本文将Bootstrap重抽样的次数设定为10。

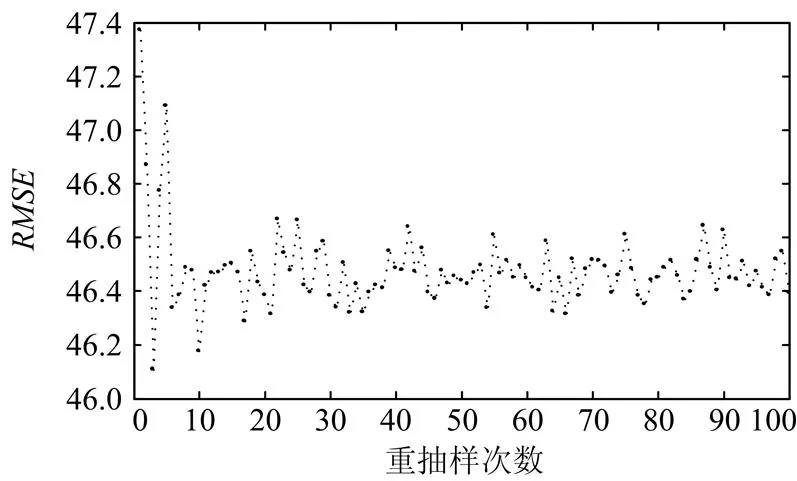
图2确定Bootstrap重抽样次数

GP属于不稳定的模型，训练数据的变化，对GPR和FITC-GPR的参数和预测结果有较大的影响，因此本文通过Bagging组合方法，分摊FITC-GPR的误差，减少偏差。图3为在50个不同的数据集上，GPR、FITC-GPR、MFITC-GPR和BFITC-GPR的预测结果对比图。由图3可知， GPR和FITC-GPR方法在不同数据集上的预测结果波动较明显，而经过Bagging组合后的MFITC-GPR和BFITC-GPR方法预测的稳定性要明显优于GPR和FITC-GPR方法。同时，提出的权重组合策略具有一定的概率意义，各个模型的权重正比于方差的倒数，有效地减少了单个不稳定模型对整体预测结果的影响。

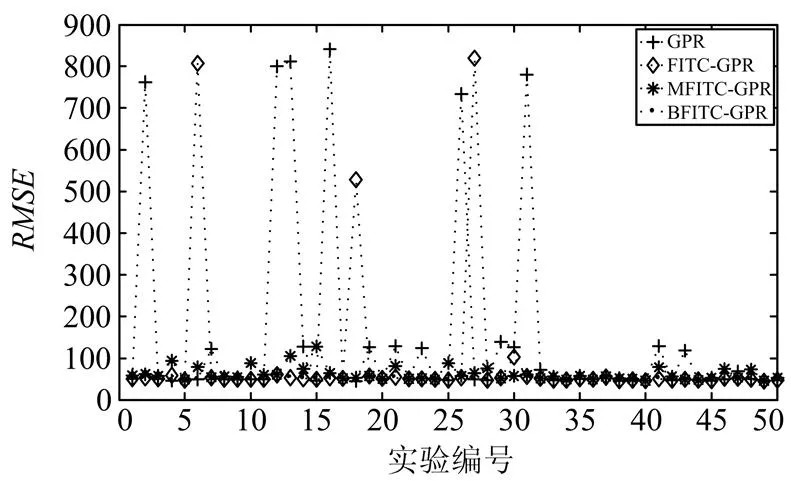
图3各种GPR的性能比较

图4为MFITC-GPR和BFITC-GPR方法预测的RMSE的对比图。由图4可知，BFITC-GPR方法的预测精度和稳定性要明显优于MFITC- GPR方法。针对GP计算量较大的缺点，引入的FITC近似方法可以有效地减小计算量。

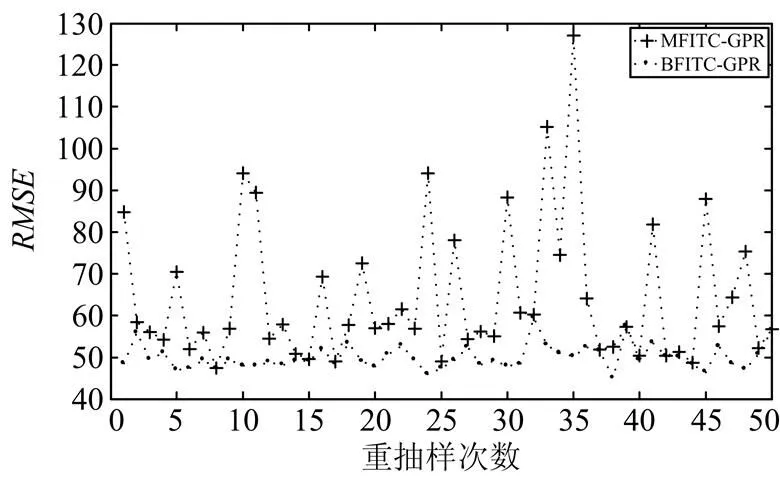
图4 BFITC-GPR和MFITC-GPR预测精度对比

图5为GPR、FITC-GPR和BFITC-GPR在不同数量的训练样本上训练所消耗的时间。随着训练样本的不断增加，GPR方法训练消耗的时间近似指数增长，而FITC-GPR、BFITC-GPR方法训练消耗的时间近似线性增长。因此经过FITC改进后的GPR方法有效地减少了GPR的计算量。综上所述，提出的基于Bagging和FITC的BFITC-GPR方法在稳定性、预测精度和训练时间的消耗上都优于传统的GPR方法。

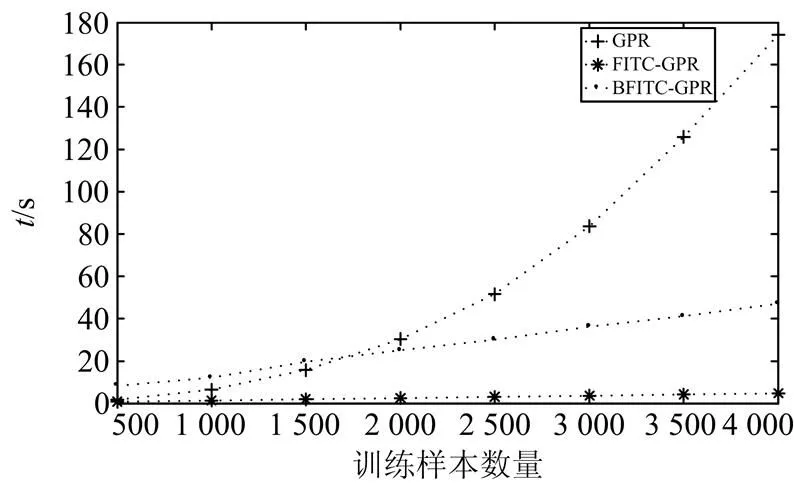
图5 GPR和FITC-GPR训练消耗时间对比

3.2 BFITC-GPR和其他方法的对比

从四个季节中分别抽取25天的数据，前24天数据用于训练模型，后一天的数据用于模型的测试。先分别使用ELM、LSSVM、BFITC-GPR方法对NWP的风速进行订正并预测功率，然后通过比较各种方法功率预测结果的RMSE和MAE来比较算法的性能。表1为春夏秋冬四个季节的数据，先使用不同的方法订正风速，再用修订后的风速预测功率后得到输出功率的和。

表1不同方法对功率的预测结果

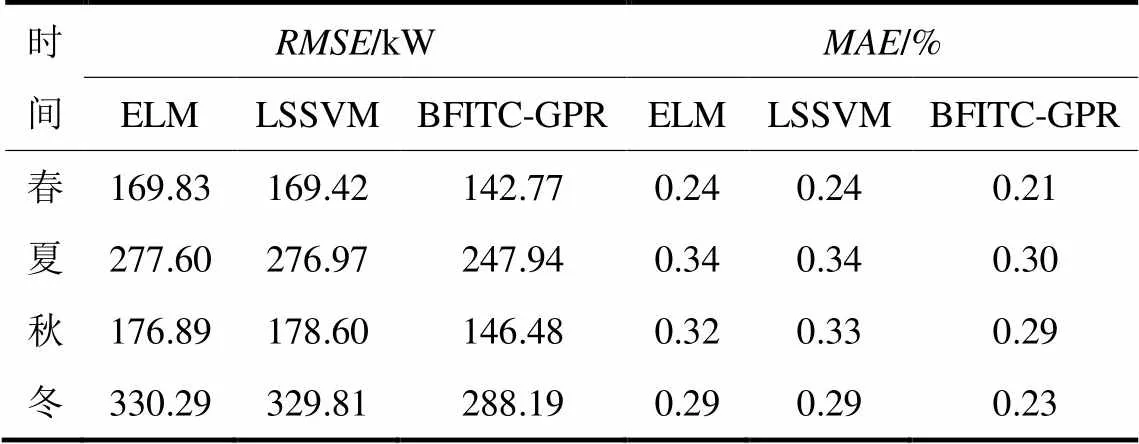
Table 1 Different methods of power prediction

春秋季节风速较稳定，而夏冬季节风速波动较明显，由表1可知，春秋季节预测的RMSE要优于夏冬季节。虽然夏季和冬季风速波动都较大，但夏季的平均风速要小于冬季的平均风速，因而出现了夏季的小于冬季，而却大于冬季的现象。四个季节中，各个算法的和都波动较大，但在每个季节上BFITC-GPR的预测精度都高于ELM和LSSVM方法的预测精度。

图6为四个季节中提前一天的功率预测值、实际值及置信区间。BFITC-GPR方法功率预测分布中，均值表示对实际功率逼近，方差表示对预测值的不确定性的量化。图6中实际功率和预测功率大部分都位于95%的置信区间内，说明BFITC- GPR对预测的不确定性给出了准确的量化。

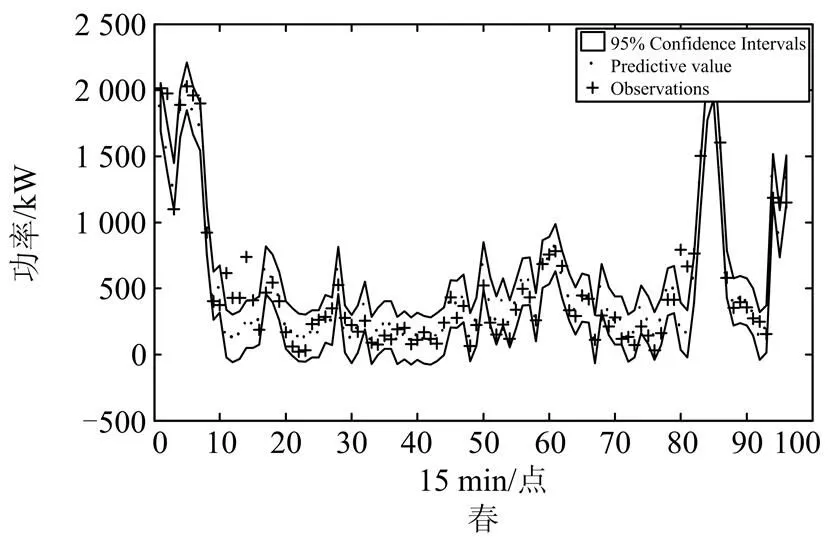
准确的置信区间可以在一定程度上反映发电功率的走势和波动范围，对风电的调度等有较大的参考价值。因此本文提出的BFITC-GPR方法，不仅在功率预测的精度上较ELM、LSSVM方法有所提高，且对预测的不确定性能够进行准确的量化，具有一定的实用价值。

4 总结

在短期风电功率预测中，单一的预测模型往往无法全面地解释风力发电整个过程的变化。同时，风速对应的功率常分布在一定范围内，而非一个固定值。针对以上问题，提出的BFITC-GPR方法将模型组合和不确定性量化结合起来，对功率的概率分布进行预测。

实验表明，基于Bagging和FITC的GPR方法在稳定性、预测精度和训练时间的消耗上都优于传统的GPR方法。在风电功率预测中，BFITC-GPR方法的预测精度较ELM、LSSVM方法有明显的提高，并可以给出较准确的置信区间。但从春、夏、秋、冬四个季节的预测结果可知，春秋季节风速较稳定，夏冬季节风速波动较明显，在模型拟合方面还需要考虑不同季节风的特征。综上所述，BFITC-GPR方法既考虑了对风电功率预测过程中的不确定性的量化，又考虑了预测精度，在风电功率预测中具有一定的实用价值。

[1] 薛禹胜, 郁琛, 赵俊华, 等. 关于短期及超短期风电功率预测的评述[J]. 电力系统自动化, 2015, 39(6): 141-150.

XUE Yusheng, YU Chen, ZHAO Junhua, et al. A review on short-term and ultra-short-term wind power prediction[J]. Automation of Electric Power Systems, 2015, 39(6): 141-150.

[2] 甘迪, 柯德平, 孙元章, 等. 基于集合经验模式分解和遗传-高斯过程回归的短期风速概率预测[J]. 电工技术学报, 2015, 30(11): 138-147.

GAN Di, KE Deping, SUN Yuanzhang, et al. Short -term wind speed probabilistic forecasting based on EEMD and coupling GA-GPR[J]. Transactions of China Electrotechnical Society, 2015, 30(11): 138-147.

[3] 肖迁, 李文华, 李志刚, 等. 基于改进的小波-BP神经网络的风速和风电功率预测[J]. 电力系统保护与控制, 2014, 42(15): 80-86.

XIAO Qian, LI Wenhua, LI Zhigang, et al. Wind speed power prediction based on improved wavelet-BP neural network[J]. Power System Protection and Control, 2014, 42(15): 80-86.

[4] 王新, 孟玲玲. 基于EEMD-LSSVM的超短期负荷预测[J]. 电力系统保护与控制, 2015, 43(1): 61-66.

WANG Xin, MENG Lingling. Ultra-short-term load forecasting based on EEMD-LSSVM[J]. Power System Protection and Control, 2015, 43(1): 61-66.

[5] 刘爱国, 薛云涛, 胡江鹭, 等. 基于GA优化SVM的风电功率的超短期预测[J]. 电力系统保护与控制, 2015, 43(2): 90-95.

LIU Aiguo, XUE Yuntao, HU Jianglu, et al. Ultra- short-term wind power forecasting based on SVM optimized by GA[J]. Power System Protection and Control, 2015, 43(2): 90-95.

[6] 王丽婕, 冬雷, 高爽. 基于多位置NWP与主成分分析的风电功率短期预测[J]. 电工技术学报, 2015, 30(5): 79-84.

WANG Lijie, DONG Lei, GAO Shuang. Wind power short-term prediction based on principal component analysis of NWP of Multiple locations[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 79-84.

[7] CHEN N, QIAN Z, NABNEY I T, et al. Wind power forecasts using Gaussian processes and numerical weather prediction[J]. IEEE Transactions on Power Systems, 2014, 29(2): 656-665.

[8] 王恺, 关少卿, 汪令祥, 等. 基于模糊信息粒化和最小二乘支持向量机的风电功率联合预测建模[J]. 电力系统保护与控制, 2015, 43(2): 26-32. WANG Kai, GUAN Shaoqing, WANG Lingxiang, et al. A combined forecasting model for wind power prediction based on fuzzy information granulation and least squares support vector machine[J]. Power System Protection and Control, 2015, 43(2): 26-32.

[9] WAN C, XU Z, PINSON P, et al. Probabilistic forecasting of wind power generation using extreme learning machine[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1033-1044.

[10] 王松岩, 于继来. 风速与风电功率的联合条件概率预测方法[J]. 中国电机工程学报, 2011, 31(7): 7-15.

WANG Songyan, YU Jilai. Joint conditions probability forecast method for wind speed and wind power[J]. Proceedings of the CSEE, 2011, 31(7): 7-15.

[11]SCHÖLKOPF B, HERBRICH R, SMOLA A, et al. Gaussian processes for machine learning[J]. International Journal of Neural Systems, 2006, 14(6): 3011-3015.

[12] CHEN T, MORRIS J, MARTIN E. Gaussian process regression for multivariate spectroscopic calibration[J]. Chemometrics and Intelligent Laboratory Systems, 2007, 87(1): 59-71.

[13] GROOT P, LUCAS P. Gaussian process regression with censored data using expectation propagation[C] // Sixth European Workshop on Probabilistic Graphical Models, 2012.

[14] QUIÑONERO-CANDELA J, RASMUSSEN, C E. A unifying view of sparse approximate Gaussian process regression[J]. Journal of Machine Learning Research, 2005, 6: 1939-1959.

[15] CHEN T, REN J. Bagging for Gaussian process regression[J]. Neurocomputing, 2009, 72(7): 1605-1610.

[16] TRESP V. A Bayesian committee machine[J]. Neural Computation, 2000, 12(11): 2719-2741.

[17]徐曼, 乔颖, 鲁宗相. 短期风电功率预测误差综合评价方法[J]. 电力系统自动化, 2011, 35(12): 20-26.

XU Man, QIAO Ying, LU Zongxiang. A comprehensive error evaluation method for short-term wind power prediction[J]. Automation of Electric Power Systems, 2011, 35(12): 20-26.

(编辑 葛艳娜)

A combination method of short-term wind power forecasting based on improved GPR and Bagging

ZHANG Yingchao1, 2, GUO Xiaojie1, DENG Hua1, 2

(1. School of Information and Control, Nanjing University of Information Science & Technology, Nanjing 210044, China; 2. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters,Nanjing University of Information Science & Technology, Nanjing 210044, China)

In order to improve the accuracy of short-term wind power forecasting and quantify the uncertainty of power prediction, a combination forecasting method based on Gaussian Process Regression (GPR) and Bootstrap Aggregation (Bagging) is proposed. For the instability and large computing of GPR, Bagging and Fully Independent Training Conditional Approximation (FITC) are introduced. Meanwhile, a new weight strategy based on Bayesian Committee Machine (BCM) is raised. Experiments show that, GPR method which based on Bagging and FITC is better than the traditional method in the stability, precision and training time consuming. Furthermore the improved GPR can get a more accurate confidence interval, and the prediction accuracy of the proposed method also has improved significantly compared with ELM and LSSVM in the wind power prediction.

GPR; Bagging; short-term wind power forecast; uncertainty quantification; BCM

10.7667/PSPC152072

2015-11-27；

2016-01-20

张颖超(1960-)，男，教授，博士生导师，研究方向为复杂系统建模与评估、气象服务效益研究、风电功率预测、气象数据质量控制等；E-mail: yc.nim@163.com

郭晓杰(1988-)，男，通信作者，硕士研究生，研究方向为短期风电功率预测；E-mail: gxj_workmail@163.com

邓 华(1977-)，男，工程师，博士研究生，研究方向为风电功率预测。E-mail: denghua@nuist.edu.cn

江苏省六大人才高峰项目(WLW-021)；国家公益性行业(气象)科研专项项目(GYHY201106040)