基于近似熵的电力系统负荷预测误差分析

杨 茂，董骏城，罗 芫，赵伟男



基于近似熵的电力系统负荷预测误差分析

杨 茂1，董骏城1，罗 芫2，赵伟男3

(1.东北电力大学电气工程学院，吉林 吉林 132012; 2.国网辽宁省电力有限公司抚顺供电公司， 辽宁 抚顺 113000; 3.国网黑龙江省电力有限公司大庆供电公司，黑龙江 大庆 163000)

为深入探究负荷时间序列预测误差的影响因素，提高负荷预测精度，提出近似熵算法，用于定量刻画负荷时间序列的规律性，全面认识负荷预测误差的成因。采用近似熵算法对负荷时间序列进行分析，确定其规律性的强弱。在此基础上，针对负荷时间序列的规律性与预测误差之间的关系进行研究。算例分析结果表明，近似熵算法可以有效刻画负荷时间序列的规律性，且负荷时间序列的规律性与其预测误差之间有着较强的相关性，证明了方法的正确性和有效性。

负荷时间序列；负荷预测；规律性；近似熵；预测误差

0 引言

在电力系统不断完善的过程中，负荷预测已经成为了一个独立的、不可或缺的一部分，它是电力系统规划的前提性工作。其中，短期的电力负荷预测主要是指对未来几小时、1天至几天的电力负荷进行预报，其既可以为电力系统的安全运行提供保障，同时也可以在市场环境下的电力系统进行编排调度计划和交易计划时提供辅助[1-2]。一直以来，预测方法被认为是提高预测精度的最主要途径，许多学者在预测方法上面进行了大量的研究，提出了多种具有较好预测精度的模型。

较为传统的预测方法有：人工神经网络法[3-4]、回归分析法[5-6]、时间序列法[7-8]、组合预测法[9-11]等。除此之外，文献[12]提出了一种综合负荷预测法，此方法的理论基础是子空间旋转矢量不变技术(ESPRIT)，该技术的频谱分辨率较好，能够有效地降低原序列维数，从而得到更高的预测精度；文献[13]提出了温度修正模型，通过拟合温升曲线、求解负荷温度弹性系数来确定高温日的界限温度，同时给出了利用相关系数求解最大累计天数和累积效应系数的方法。文献[14-16]分别提出了基于数据挖掘预处理的改进短期电力负荷预测方法、基于核函数极限学习机的微电网短期负荷预测方法和基于离散Fréchet距离与LS-SVM相结合的短期负荷预测方法，提高了预测的精度；文献[17]提出了一种将混合语言信息群决策方法和BP神经网络相结合的城市电力负荷密度预测法，其预测结果具有较高的可信度。文献[18]将人工蜂群(ABC)算法应用到中长期电力负荷预测中，通过与组合预测模型相结合，对组合预测目标函数进行优化权重求解，预测精度有很大提高；文献[19]是在海量数据的背景下进行的短期负荷预报，该研究基于云计算平台和局部加权线性回归，建立了并行局部加权线性回归模型，此法在减少负荷预测时间和提高预测精度方面有较好的表现。虽然“好”的预测方法在一定范围内可以提高预测精度，但是无论是多么高明的预测方法都不能实现负荷的准确无差预测。原因就在于，负荷时间序列的预测精度受多种因素的影响，除了与所采用的预测模型有关外，还与负荷时间序列本身的规律性有关，而后者正是本文研究的重点。

文献[20]提出了基于局域波与近似熵的负荷分析方法，先对负荷时间序列进行局域波分解，然后利用近似熵提取各分量及余量的特征参数，从而研究各分量的物理含义，最后分析了气象因素对负荷的影响，其研究的重心在于分析负荷构成及负荷影响因素；文献[21]通过计算各分量以及不同负荷类型之间的近似熵，分析其非线性度以及不规则度，从而对各分量进行类型识别。该文则主要侧重在基于近似熵来探究负荷时间序列自身规律性与总的预测误差之间的关系。不同于以上文献，本文的研究工作主要通过相空间理论对负荷时间序列进行重构，再利用近似熵算法对重构后的负荷时间序列进行分析，通过近似熵量化分析负荷时间序列的复杂程度，即：负荷时间序列规律性越差，即产生新模式的概率越大，其近似熵越大，当对其进行预测时，预测精度越低。

本文首先分析了负荷时间序列预测误差的构成；并利用近似熵对负荷时间序列自身的规律性进行分析，在此基础上，进一步探究负荷自身规律性与总的预测误差之间的关系。对负荷时间序列规律性的准确把握可有效指导负荷预测方法的选择和改进，为提高预测精度提供理论依据。

1 负荷时间序列预测误差的构成

综上，在一次负荷预测中，总的预测误差由两部分产生，一部分为由预测方法的优劣决定的建模误差，预测方法越好，其值越小；另一部分为由负荷本身的规律性决定的外推误差，规律性越好，产生新模式的几率越小，其值就越小。可见，负荷预测的精度除了与所采用的预测模型有关，还与负荷时间序列本身的规律性有关，一味地追求通过改进预测模型来减小建模误差是不能实现无差预测的，对负荷本身规律性的研究也同样具有重要意义。

2 近似熵

近似熵(Approximate Entropy)是Pincus为了刻画信号序列的复杂性而提出的，可以用来度量序列中出现新模式的概率大小[23]。

近似熵采用的是相空间重构的思想，其计算步骤如下[24]。

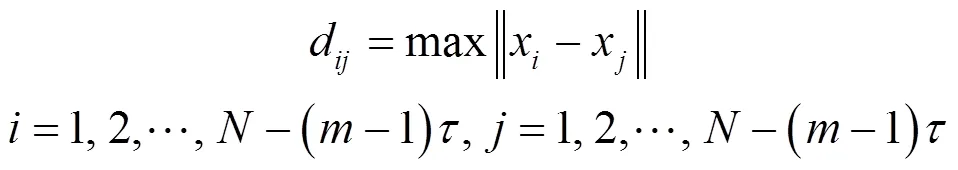
Step6：理论上近似熵的定义为

需要指出的是近似熵值的大小与序列的幅值无关，只与序列的复杂程度相关[25]。这是由于近似熵刻画的是序列在模式上的自相似程度，只具有相对含义而与绝对的幅值无关，是一种无量纲指标，并且近似熵值越大，代表序列复杂性越强，产生新模式的概率越大，即序列规律性越差[26]。

3 算例分析

本文对负荷规律性的分析是在短期负荷预测的背景下进行的，取某地区一个星期七天的负荷时间序列进行算例分析，负荷数据的时序图如图1所示，采样间隔为15 min。

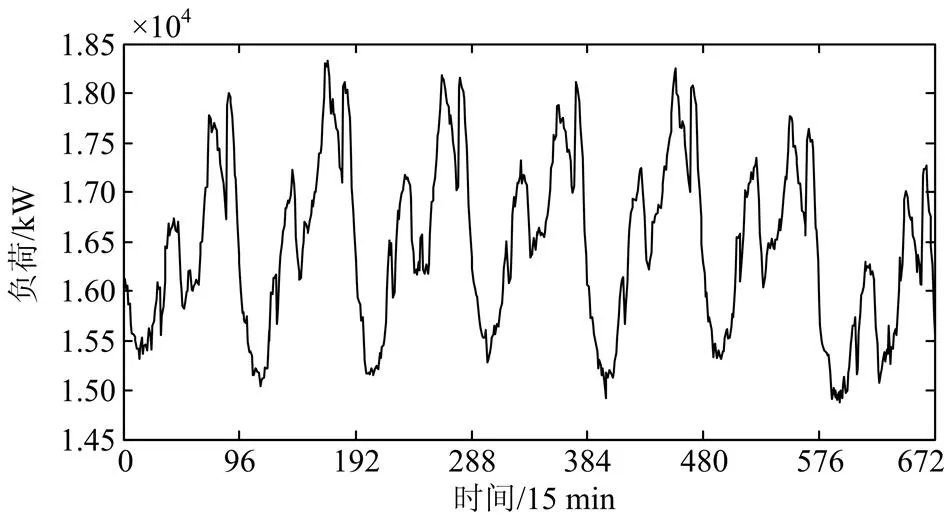
图1 负荷序列时序图

为了分析负荷时间序列的规律性，分别计算各天负荷时间序列的近似熵，结果如表1所示。其中，Pincus[23]认为，当，一般取原始时间序列标准差的0.1~0.2倍时，近似熵值具有较合理的统计特性，因此本文取，取原始时间序列标准差的0.2倍。

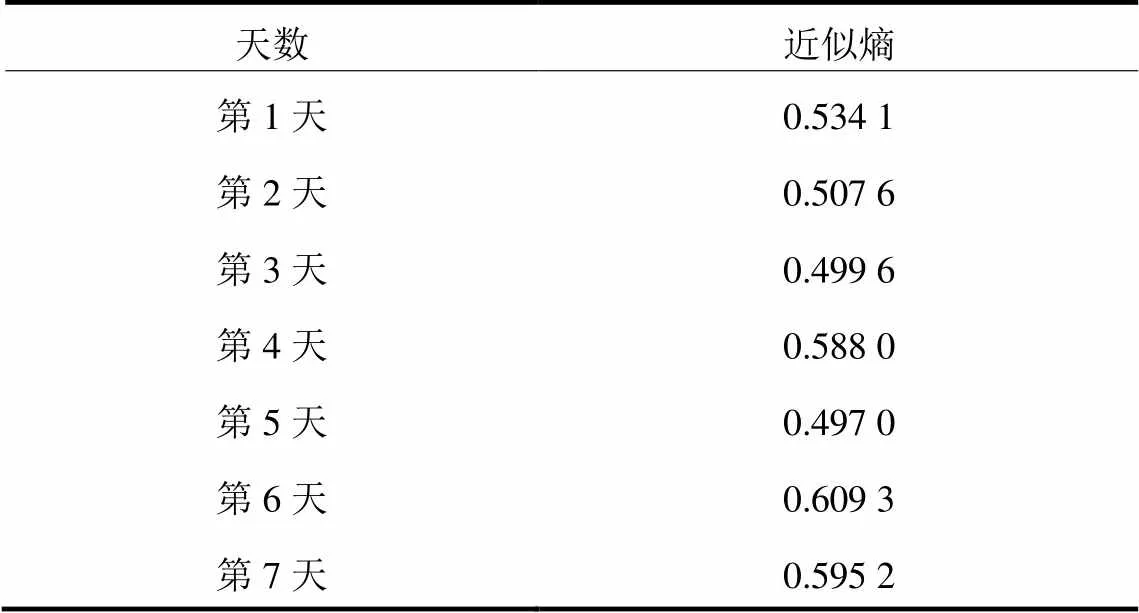
表1 各天负荷时间序列的近似熵值

为了分析负荷时间序列的规律性与预测误差之间的关系，本文采用滑动平均法，对各天的负荷时间序列进行多步滚动预测[27]，并选取准确率和全天预测结果均方根误差率作为预测结果评价指标，和的计算式分别如式(8)和式(9)所示。越大，越小，则预测精度越高。

对各天负荷时间序列利用滑动平均法进行多步滚动预测的结果如表2所示，其中，第1天的负荷序列被用作第2天负荷预测的建模域，所以不进行预测。图2和图3分别为各天近似熵与各天预测准确率和全天预测结果均方根误差率的对比图。观察图2和图3可以发现，近似熵与准确率的变化趋势是完全相反的，而与全天预测结果均方根误差率的变化趋势完全相同，即近似熵增大时，减小，增大；而当近似熵减小时，增大，减小。进一步计算求得：近似熵与之间的相关系数为-0.602 2；近似熵与之间的相关系数为0.649 9。即近似熵与和都具有较强的相关性，且与呈负相关，与呈正相关。

综上，负荷时间序列的规律性与其预测误差之间有着较强的相关性。此相关性可描述为：负荷时间序列规律性越差，即产生新模式的概率越大，其近似熵越大，当对其进行预测时，准确率越低，全天预测结果均方根误差率越大。

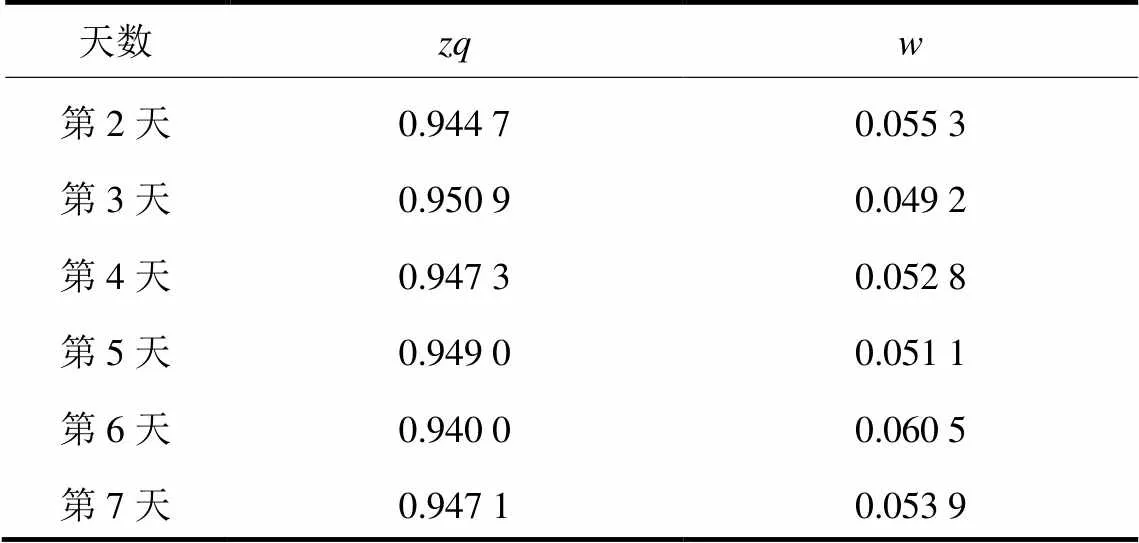
表2 各天预测结果统计表

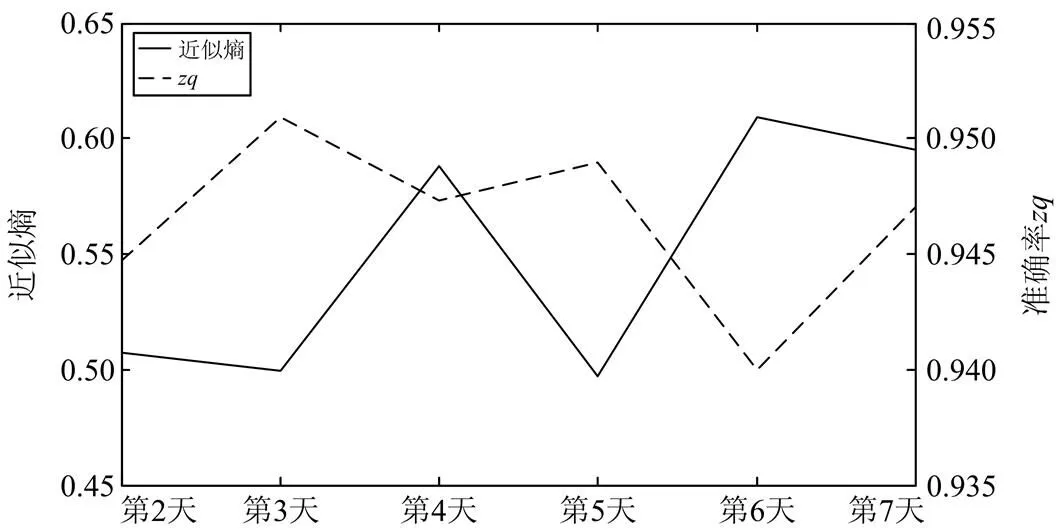
图2 各天近似熵与准确率对比图

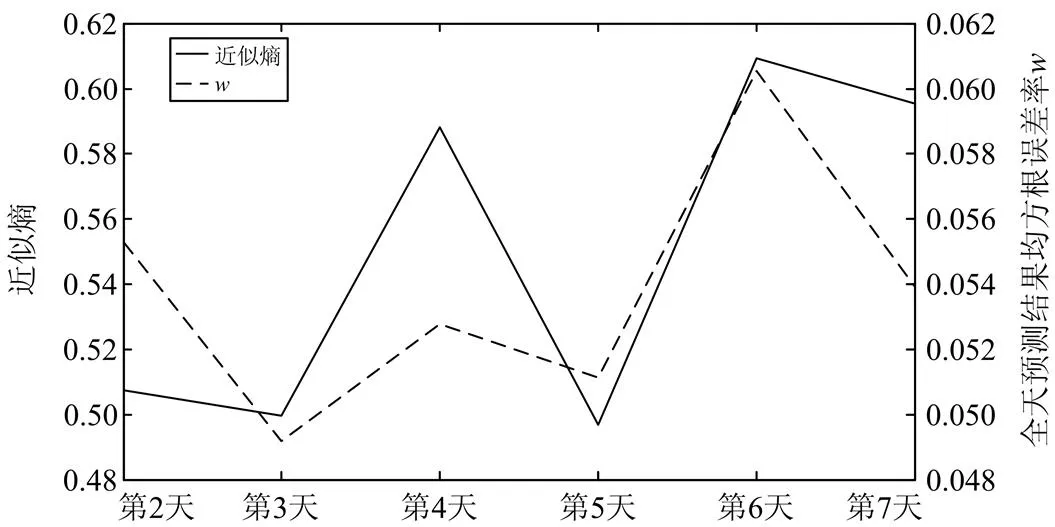
图3 各天近似熵与全天预测结果均方根误差率对比图

4 结论

本文对负荷时间序列预测误差的构成进行分析，在此基础上指出了对负荷本身规律性进行研究的重要性。并分析了负荷时间序列自身规律性与预测误差之间的关系，得到了以下结论。

(1) 总的负荷预测误差由两部分组成：一部分为由预测方法的优劣决定的建模误差；另一部分为由负荷本身的规律性决定的外推误差。

(2) 近似熵可以有效地刻画负荷时间序列的规律性，其值越大，表明序列复杂性越强，产生新模式的概率越大，即序列规律性越差，对负荷时间序列规律性的准确把握可有效指导负荷预测方法的选择和改进，为提高预测精度提供理论依据。

(3) 负荷时间序列的近似熵值与其预测准确率和全天预测结果均方根误差率都具有较强的相关性，且与呈负相关，与呈正相关。换言之，负荷时间序列的近似熵值越大，当对其进行预测时，准确率越低，全天预测结果均方根误差率越大。

[1] 康重庆, 夏清, 刘梅. 电力系统负荷预测[M]. 北京: 中国电力出版社, 2007.

[2] 廖旎焕, 胡智宏, 马莹莹, 等. 电力系统短期负荷预测方法综述[J]. 电力系统保护与控制, 2011, 39(1): 147-152.

LIAO Nihuan, HU Zhihong, MA Yingying, et al. Review of the short-term load forecasting methods of electric power system[J]. Power System Protection and Control, 2011, 39(1): 147-152.

[3] 张平, 潘学萍, 薛文超. 基于小波分解模糊灰色聚类和BP神经网络的短期负荷预测[J]. 电力自动化设备, 2012, 32(11): 121-125.

ZHANG Ping, PAN Xueping, XUE Wenchao. Short-term load forecasting based on wavelet decomposition, fuzzy gray correlation clustering and BP neural network[J]. Electric Power Automation Equipment, 2012, 32(11): 121-125.

[4] 陈刚, 周杰, 张雪君, 等. 基于BP与RBF级联神经网络的日负荷预测[J]. 电网技术, 2009, 33(12): 101-105.

CHEN Gang, ZHOU Jie, ZHANG Xuejun, et al. A daily load forecasting methods based on cascaded back propagation and radial basis function neural networks[J]. Power System Technology, 2009, 33(12): 101-105.

[5] 瞿迪庆, 陈红敏, 吕理想. 模糊线性回归方法在节假日短期负荷预测中的应用[J]. 电力需求侧管理, 2013, 15(3): 16-19.

QU Diqing, CHEN Hongmin, LÜ Lixiang. Holidays short-term load forecasting using fuzzy linear regression method[J]. Demand Side Management, 2013, 15(3): 16-19.

[6] 黄玉龙, 刘明波, 郑文杰, 等. 基于可信区间的模糊线性回归动态负荷参数预测[J]. 电工技术学报, 2015, 30(24): 196-205.

HUANG Yulong, LIU Mingbo, ZHENG Wenjie, et al. Dynamic load model parameter prediction using confidence-interval-based fuzzy linear regression[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 196-205.

[7] 万坤, 柳瑞禹. 区间时间序列向量自回归模型在短期电力负荷预测中的应用[J]. 电网技术, 2012, 36(11): 77-81.

WAN Kun, LIU Ruiyu. Application of interval time-series vector autoregressive model in short-term load forecasting[J]. Power System Technology, 2012, 36(11): 77-81.

[8] 崔和瑞, 彭旭. 基于ARIMAX模型的夏季短期电力负荷预测[J]. 电力系统保护与控制, 2015, 43(4): 108-114.

CUI Herui, PENG Xu. Summer short-term load forecasting based on ARIMAX model[J]. Power System Protection and Control, 2015, 43(4): 108-114.

[9] 杨茂, 贾云彭, 钱为, 等. 基于动态权重的风电功率组合预测方法研究[J]. 东北电力大学学报, 2013, 33(1/2): 131-136.

YANG Mao, JIA Yunpeng, QIAN Wei, et al. A combination method research for wind power predication based on dynamic weight[J]. Journal of Northeast Dianli University, 2013, 33(1/2): 131-136.

[10] 杨茂, 孙涌, 孙兆键, 等. 风电场大规模数据管理系统设计与研发[J]. 东北电力大学学报, 2014, 34(2): 27-31.

YANG Mao, SUN Yong, SUN Zhaojian, et al. Design and development of large-scale data management system of wind farm[J]. Journal of Northeast Dianli University, 2013, 34(2): 27-31.

[11] 王新, 孟玲玲. 基于EEMD-LSSVM的超短期负荷预测[J]. 电力系统保护与控制, 2015, 43(1): 61-66.

WANG Xin, MENG Lingling. Ultra-short-term load forecasting based on EEMD-LSSVM[J]. Power System Protection and Control, 2015, 43(1): 61-66.

[12] 马哲, 舒勤. 基于ESPRIT分解算法的短期电力负荷预测[J]. 电力系统保护与控制, 2015, 43(7): 90-96.

MA Zhe, SHU Qin. Short-term load forecasting based on ESPRIT integrated algorithm[J]. Power System Protection and Control, 2015, 43(7): 90-96.

[13] 高赐威, 李倩玉, 苏卫华, 等. 短期负荷预测中考虑积温效应的温度修正模型研究[J]. 电工技术学报, 2015, 30(4): 242-248.

GAO Ciwei, LI Qianyu, SU Weihua, et al. Temperature correction model research considering temperature cumulative effect in short-term load forecasting[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 242-248.

[14] 崔和瑞, 宋秀莉, 葛曼倩. 基于数据挖掘的FNN短期电力负荷预测方法研究[J]. 电力系统保护与控制, 2009, 37(22): 54-57.

CUI Herui, SONG Xiuli, GE Manqian. Research on FNN short-term electric load forecasting based on data mining technology[J]. Power System Protection and Control, 2009, 37(22): 54-57.

[15] 陈超, 黄国勇, 范玉刚, 等. 基于离散Fréchet距离和LS-SVM的短期负荷预测[J]. 电力系统保护与控制, 2014, 42(5): 142-147.

CHEN Chao, HUANG Guoyong, FAN Yugang, et al. Short-term load forecasting based on discrete Fréchet distance and LS-SVM[J]. Power System Protection and Control, 2014, 42(5): 142-147.

[16] 刘念, 张清鑫, 刘海涛. 基于核函数极限学习机的微电网短期负荷预测方法[J]. 电工技术学报, 2015, 30(8): 218-224.

LIU Nian, ZHANG Qingxin, LIU Haitao. Online short-term load forecasting based on ELM with kernel algorithm in micro-grid environment[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 218-224.

[17] 周胜瑜, 周任军, 李红英, 等. 采用混合语言信息群决策的电力负荷密度预测法[J]. 电力系统保护与控制, 2014, 42(7): 15-22.

ZHOU Shengyu, ZHOU Renjun, LI Hongying, et al. Power load density prediction method of using group decision-making of mixed language information[J]. Power System Protection and Control, 2014, 42(7): 15-22.

[18] 陈强, 金小明, 姚建刚, 等. 基于改进ABC算法的中长期电力负荷组合预测[J]. 电力系统保护与控制, 2014, 42(23): 113-117.

CHEN Qiang, JIN Xiaoming, YAO Jiangang, et al. Improved artificial bee colony algorithm applied to medium and long-term load combination forecasting[J]. Power System Protection and Control, 2014, 42(23): 113-117.

[19] 张素香, 赵丙镇, 王风雨, 等. 海量数据下的电力负荷短期预测[J]. 中国电机工程学报, 2015, 35(1): 37-42.

ZHANG Suxiang, ZHAO Bingzhen, WANG Fengyu, et al. Short-term power load forecasting based on big data[J]. Proceedings of the CSEE, 2015, 35(1): 37-42.

[20] 栗然, 陆凤怡, 徐宏锐, 等. 基于局域波与近似熵的负荷分析方法[J]. 中国电机工程学报, 2010, 30(25): 51-58.

LI Ran, LU Fengyi, XU Hongrui, et al. Novel approach for load analysis based on local wave and approximate entropy[J]. Proceedings of the CSEE, 2010, 30(25): 51-58.

[21] 赵文华. 基于局域波的特殊性负荷短期预测研究分析[D]. 太原: 太原理工大学, 2014.

ZHAO Wenhua. The analysis of special short-term load forecasting based on local wave[D]. Taiyuan: Taiyuan University of Technology, 2014.

[22] 穆钢, 侯凯元, 杨右虹, 等. 一种内蕴误差评价的负荷预报方法[J]. 电力系统自动化, 2001, 25(22): 37-40.

MU Gang, HOU Kaiyuan, YANG Youhong, et al. A load forecasting method based on intrinsic error evaluation[J]. Automat ion of Electric Power Systems, 2001, 25(22): 37-40.

[23] PINCUS S M. Approximate entropy as a measure of system complexity[J]. Proceeding of the National Academy Sciences USA, 1991, 88(6): 2297-2301.

[24] 吕勇, 徐金梧, 李友荣. 递归图和近似熵在设备故障信号复杂度分析中的应用[J]. 机械强度, 2006, 28(3): 317-321.

LÜ Yong, XU Jinwu, LI Yourong. Application of recurrence plot and approximate entropy on complexity analysis[J]. Journal of Mechanical Strength, 2006, 28(3): 317-321.

[25] 胡红英, 马孝江. 局域波近似熵及其在机械故障诊断中的应用[J]. 振动与冲击, 2006, 25(4): 38-40.

HU Hongying, MA Xiaojiang. Application of local wave approximate entropy in mechanical fault diagnosis[J]. Journal of Vibration and Shock, 2006, 25(4): 38-40.

[26] 符玲, 何正友, 麦瑞坤, 等. 近似熵算法在电力系统故障信号分析中的应用[J]. 中国电机工程学报, 2008, 28(28): 68-74.

FU Ling, HE Zhengyou, MAI Ruikun, et al. Application of approximate entropy to Fault signal analysis in electric power system[J]. Proceedings of the CSEE, 2008, 28(28): 68-74.

[27] 严干贵, 王东, 杨茂, 等. 两种风电功率多步预测方式的分析及评价[J]. 东北电力大学学报, 2013, 33(1): 126-130.

YAN Gangui, WANG Dong, YANG Mao, et al. The analysis and evaluation of two ways for multi-step wind power prediction[J]. Journal of Northeast Dianli University, 2013, 33(1): 126-130.

(编辑 葛艳娜)

Study of power system load forecasting errors based on approximate entropy

YANG Mao1, DONG Juncheng1, LUO Yuan2, ZHAO Weinan3

(1. School of Electrical Engineering, Northeast Dianli University, Jilin 132012, China; 2. Fushun Power Supply Bureau, State Grid Liaoning Electric Power Ltd., Fushun 113000, China; 3. Daqing Power Supply Bureau,State Grid Heilongjiang Electric Power Ltd., Daqing 163000, China)

To further explore the influence factors of load time sequence forecasting errors and improve the accuracy of load forecasting, an approximate entropy algorithm is proposed for characterizing the regularity of load time series quantitatively and recognizing the causes for load forecasting errors fully.Approximate entropy algorithm is applied to analyze load time series and determine the regularity of it. Based on the above research, this paper carries out the related research according to the relationship between the regularity and forecasting errors of load time series. The results show that, approximate entropy algorithm can describe the regularity of load time series effectively, and there is a strong correlation between regularity of load time series and load forecasting errors, proving the correctness and validity of the method.

This work is supported by National Key Basic Research Program (973 Program) (No. 2013CB228201) and National Natural Science Foundation of China (No. 51307017).

load time series;load forecasting; regularity; approximate entropy; forecasting errors

10.7667/PSPC152071

2015-11-27；

2016-02-25

杨 茂(1982-)，男，博士，副教授，硕士生导师，研究方向为风电功率预测技术；E-mail: yangmao820@163.com

董骏城(1990-)，男，硕士研究生，研究方向为电力系统分析与风力发电技术；E-mail: 814968539@qq.com

罗 芫(1987-)，女，工程师，研究方向为电力系统分析。

国家重点基础研究发展计划项目(973计划)(2013CB228201)；国家自然科学基金(51307017)；吉林省科技发展计划(20140520129JH)；吉林省产业技术研究与开发专项项目(2014Y124)