消除零模波速影响的配电网单端行波故障测距算法

何 晓，雷 勇，周聪聪，周 凯，王 鹏



消除零模波速影响的配电网单端行波故障测距算法

何 晓，雷 勇，周聪聪，周 凯，王 鹏

(四川大学电气信息学院，四川 成都 610065)

配电网线路分支众多，末端往往具有三相不平衡负载，传统的单端行波法需在复杂的折反射波中提取故障点的反射波，不易实现。而基于模量行波速度差和基于线模行波突变这两种故障测距方法的精确度都受制于不稳定的零模波速度。基于此，将两种方法结合，利用零模检测波速度与传播距离成对应关系的特点，获得不受零模波速度影响的故障定位新方法，该方法避免了传统故障测距算法需要多次从复杂的折反射波中提取信息的缺点，能够简洁、快速、准确地对复杂的分支线路进行故障测距。此方法首先检测故障暂态行波的零模和线模分量到达首端的时间差，然后在首端对三相同时注入相同的高压脉冲并检测线模行波首个波头到达检测点的时间，进而利用稳定的线模波速度进行故障距离的测量。最后，利用PSCAD仿真验证了所提方法基本不受故障位置、过渡电阻大小以及故障初相角的影响，各种情况下绝对误差均在100 m之内。

配电网；故障测距；零模波速度；小波变换；波头

0 引言

电网故障中单相接地故障占了80%以上，且由于配电网具有线路网络半径小、末端随机负荷多、线路分支繁多等特点，使得单相接地故障定位比较困难。如果不能快速准确地进行故障定位，将导致重大的经济损失，配电网单相接地故障的高效定位是一个亟待解决的难点问题[1-2]。当前国内配电网的自动化水平尚未成熟，基于自动化采集装置的定位方法尚不能在很多地区实现[3-6]，而阻抗法精度较差，受线路随机负荷影响较大[7-8]，在配电网故障定位上行波法是目前较可行且有较高研究价值的方法[9]。行波故障测距法在输电线路虽已成熟应用，但不能直接搬到配电网中使用，因为高压输电线路是一条或少数几条分支的线路，行波易于识别与分析；而配电网众多的分支会造成信号衰减及信息混叠干扰，给测距或定位方法造成了难度。

根据测量端的数量，行波故障测距通常被分为双端法和单端法[10]。双端法即D型行波法[11-12]，该方法只能对主干线路上的故障进行测距，对分支线路不太奏效，除非在每个分支末端都装设行波检测装置[13-15]，且需要GPS时钟同步，但这样则会大量增加成本。单端法中，A型行波法[16-17]由于故障点反射波会淹没在分支点折反射波中，且信号较弱，难以识别，故不易实现；行波模量速度差法[18-20]原理简单易行，只需要获取各模量的第一个波头信息，但是存在零模波速度随距离改变的问题，测距的前提是需要对具体线路进行大量的数据拟合[21]；C型行波法[22]应用在配电网中时，分支末端的三相不平衡负载会造成伪故障点的出现，使测距失效；基于线模行波突变的配电网故障测距方法[23]消除了线路多变性和不平衡负载的影响，但是从测距公式中可知，也需要同时知道线模和零模波速度才能精确测距[24]。文献[23]中以行波首个非零点作为行波到达时刻，取波速度为光速，理论上在架空线路是可行的，但是在存在干扰和采集灵敏度不够的情况下，行波首个过零点对应的波速度会显著下降，此方法会导致较大的测距误差。

根据以上方法存在的不足，同时为了避免从配电网复杂的折反射波中提取多个波头信息，在缺乏零模波速度先验知识的情况下进行故障测距，本文利用线路中线模波速较为稳定、而零模检测波速度与传播距离成对应关系的特点，联立基于模量行波速度差和基于线模行波突变的故障点定位方法，消除了测距公式中的零模波速度量，提出了一种新的消除零模波速影响的配电网单端行波故障测距算法，并得到一种新的故障测距公式。

1 行波模量分析

在任何均匀的三相输电线路中，每一点的电压和电流均满足式(1)波动方程组[25]。

求解式(1)对应的方程组，得到

求得的式(2)即为三相电路在频域中对应的波动方程组，由于三相电路之间存在着电磁耦合效应，方程组内的方程相互关联，不易直接求解该方程组，为了简化该方程的求解过程，采用卡伦鲍厄变换矩阵对式(2)进行相模变换，将电流相量和电压相量转化为对应的形式，使得变换后对应方程的各个分量相互独立，以此将三相系统分解成了三个独立的模量，易于求解。其对应的相模变换和反变换公式为

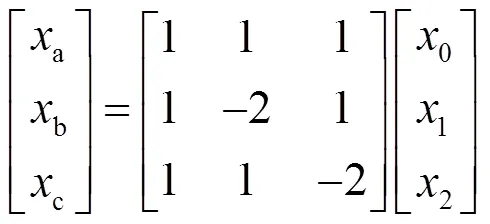
式中：a,b,c为相量；0,1,2为模量。

卡伦鲍厄矩阵变换时，三相行波对应的0模、1模和2模的含义如图1。

图1行波各模分量在三相线路上的分布情况

2  模量波速分析

模量行波对应的模波阻抗和模传播系数分别为[25]

而模行波分量的传播速度则为

对于零模，由于其特性和零序电感、零序电流密切相关；而由于大地回路集肤效应的存在，使得

行波的色散使零模行波波头的形状发生变化，因此零模波抵达的准确时刻也就难以判定，这将直接影响到故障定位的准确度。通常采用具有1阶消失矩的小波对相应的零模行波进行小波变换，小波变换的模极大值也就对应着行波的突变点。小波变换模极大值即是信号被平滑后的1阶导数的模极大值，当距离较短时，1阶导数模极大值由高频分量引起，而行波衰减常数随频率升高而增大，因而，随着传播距离的增加，高频分量部分的幅值衰减更严重，1阶导数模极大值从高频往低频转移，导致了检测波速度逐渐降低。研究表明，对于给定的线路，零模行波的检测波速随其传播距离的增加而单调减小，且几乎不受别的因素的影响[28-29]。

3 消除零模波速影响的单端行波故障测距算法

3.1 基于模量行波速度差的故障测距方法

应用模量行波的速度差进行故障测距的原理：由于零模行波和线模行波的波速度不相同，所以由故障点处产生的暂态行波途经相同的传播线路所需要的时间也不相同，所以利用对应的时间差和速度差得到测试点与故障点之间的距离，从而进行故障点的定位。如图2所示，M端为线路首端也即是测量点，线路的F点发生单相接地故障产生暂态行波，且该暂态行波同时向两端传播。由于零模和线模行波分别以不一样的波速度向首端传播，故有关系式(6)[18]。

进而有测距公式：

3.2 基于线模行波突变的故障测距方法

如果线路中的某处发生了单相接地故障，则故障点处将不再保持三相平衡状态，进而，模量系统的各个导体间将出现耦合现象。所以，当在线路首端对三相同时注入相同的高压脉冲(即注入一个零模电压行波)时，将会在故障点处产生线模反射行波，在首端也将能检测到一个线模行波的突变。如图3所示，当在首端M处注入一个高压脉冲后，将有式(8)的关系式[23]。

式中：0表示零模电压行波的波速度；0表示零模电压行波到达故障点所用的时间；1表示故障点反射回来的线模电压波的波速度；1表示故障点反射的线模电压行波到达首端所花的时间；为故障点到首端的距离；为线模电压行波首次到达首端的时刻(假定脉冲注入时刻为时间起点)。

图3基于线模行波突变的故障测距原理图

Fig. 3 Schematic of fault location method based on mutation of aerial mode traveling wave

进而有故障测距公式：

3.3 消除零模波速影响的故障测距算法

据测距公式(7)、式(9)可知，如果单独应用上述两种测距方法，若要获得精确的故障距离，不仅要检测模量行波到达首端的时间，还要确定所对应的模量行波的准确波速度。由第2章分析，线模行波波速比较稳定，可以使用实测值，但是零模行波的测量波速度则会随着距离的变化而变化，对于给定的线路，二者的关系曲线是固定不变的。由于式(7)和式(9)中的零模行波所传播的距离均为故障距离，所以它们对应的零模测量波速度也是相同值。

联立式(7)和式(9)，消去对应的零模波速度，得到新的故障测距公式：

由式(10)可知，要准确计算出故障距离，只是需要知道模量行波的到达时间和线模的波速度。本算法的整体步骤如下：

(1) 记录传播到线路首端的故障暂态行波，并经相模变换计算其对应的零模分量和线模分量；

(2) 对上一步得到的零模电压行波信号和线模电压行波信号分别进行小波变换，根据小波模极大值点获得零模行波到达时刻0，和线模行波的到达时刻1，进而求得两者的时间差D；

(3) 当线路发生故障时，在线路首端对三相同时注入相同的高压脉冲，并检测线路中反射的行波信号，通过相模变换得到相应的线模分量；

(4) 对线路中反射的线模电压行波信号进行小波变换，并取小波模极大值点处的时间作为线模行波抵达首端的时间；

(5) 将D和以及线模行波速度1(1取线路实测值)代入式(10)，求得故障距离。

4 仿真分析

本文基于PSCAD中的频率相关线路模型(frequency dependent models)进行电力网络的搭建和仿真。并将从PSCAD中得到的行波信号，导入Matlab进行相模变换和函数为Db6的小波变换。

如图4所示，为10 kV配电网的仿真线路拓扑结构图，图中字母代表线路中的节点(包括主干线两端、各分支点和分支末端)，各线路的长度如图中标注，导线型号为LGJ-240，直径是21.6 mm，直流电阻0.118 1W/m，土壤电阻率100W·m。表示线路的首端(亦是测量点)，并在各个支路的末端安装10 kV/0.4 kV的配电变压器(Dyn或Yyn联结)和三相不对称负荷。仿真过程中，注入的暂态行波信号为易于检测的高压脉冲，其对应的宽度为4 μs，幅值是10 kV，采样频率为10 MHz。线模波速度取为2.982×105km/s，则从原理而言对应的误差为14.91 m。

在线路段且距首端距离9 km处设置一个阻值为10W的单相接地故障，故障初相角为90°。故障处产生的暂态行波的零模分量和线模分量如图5(a)和图5(b)所示。利用Db6小波对其进行21尺度下的小波变换，得到其细节部分的波形以图6所示。从图6可以获得故障暂态零模分量和线模分量的第一个波头时间分别为30.6 μs和30.1 μs，对应的D=30.6 μs-30.1 μs =0.5 μs。

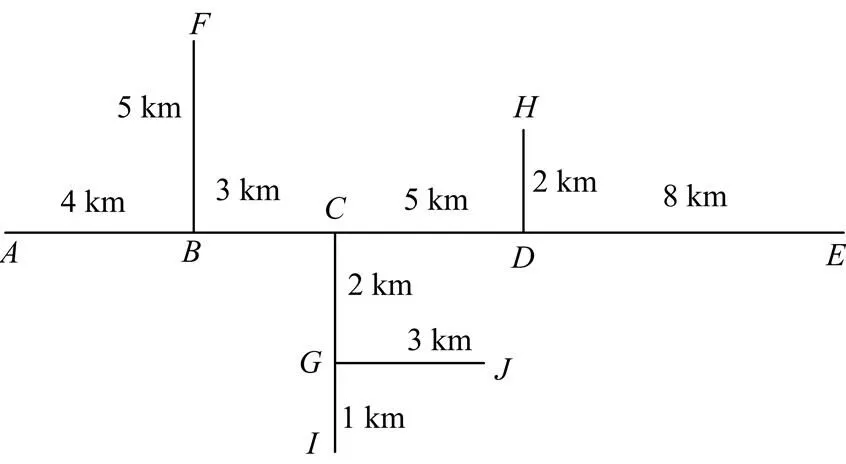
图4仿真线路的拓扑结构

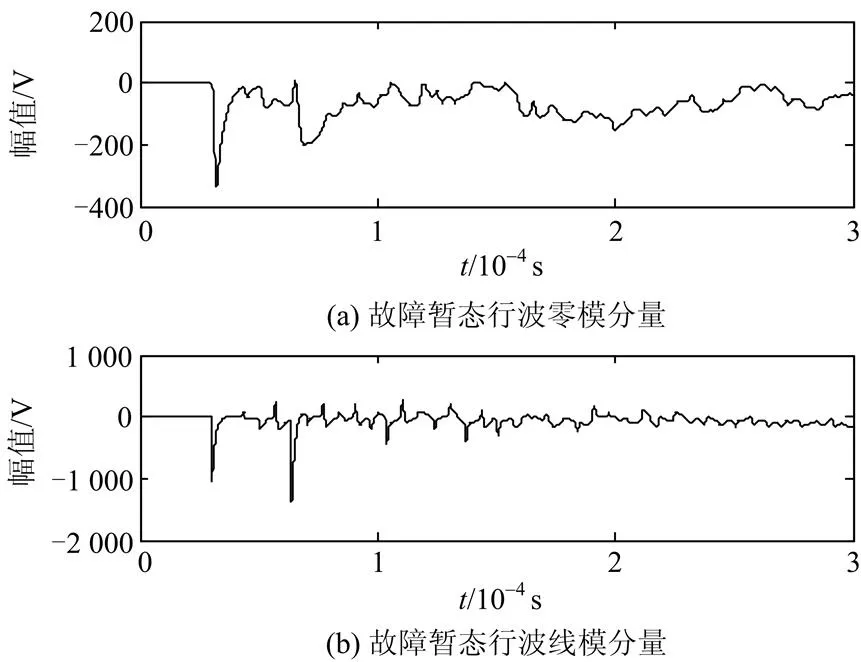
图5故障产生的暂态行波

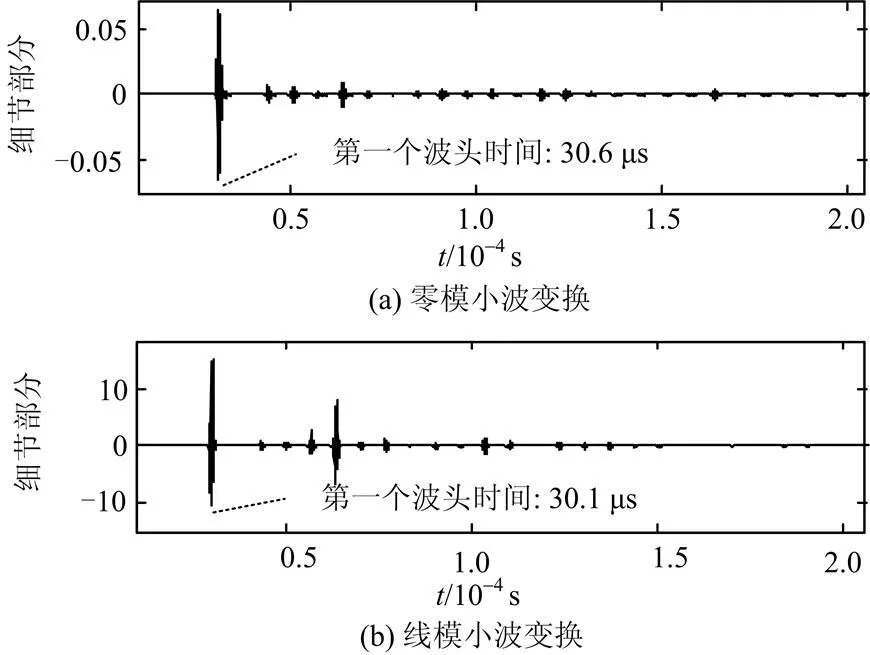
图6故障暂态行波在21尺度下的小波变换

然后在线路首端三相同时注入相同的高压脉冲，测量线模电压行波，仿真得到的波形如图7，小波变换后的波形如图8所示。由图中看到线模行波到达首端的第一个波头时刻为60.6 μs。

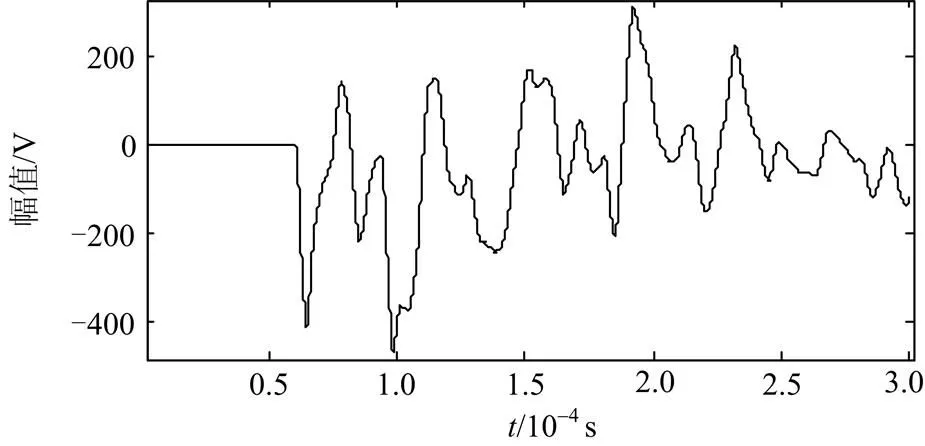
图7注入脉冲后首端的线模电压行波

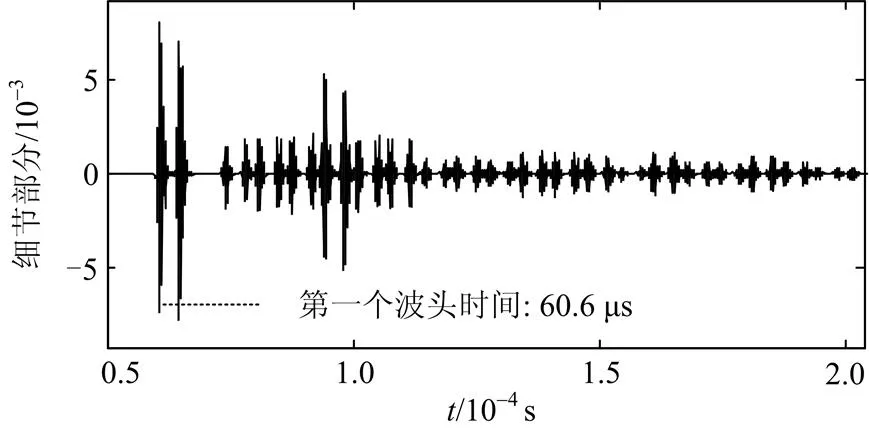
图8注入脉冲后首端的线模电压行波在21尺度下的小波变换

将D和代入式(10)，求得对应的故障距离为8.961 km，而真实故障距离为9 km，则其对应的绝对误差为39 m，在误差范围内。

同样的情况下，应用基于模量行波速度差的方法，零模波速度取为2.934×105km/s，测得故障距离为9.114 km；采用文献[23]中基于线模行波突变的方法时，测得故障距离为9.09 km。

改变故障位置、过渡电阻和故障初相角后，再分别进行仿真实验。

表1表示当保持接地电阻为10W，故障初始相角为90°不变时，改变故障位置时的实验结果。从表中可以看到，在不同故障距离的情况下，本方法都能获得较好的测距精度，误差范围比较小，而且即使故障位置接近分支点或者分支末端，也基本不受影响。而基于模量行波速度差的方法在没有拟合零模波速度的条件下，测量结果十分不稳定，误差很大；基于线模行波突变的方法也随着故障距离的增加误差逐渐增大。

表1不同故障位置的仿真结果

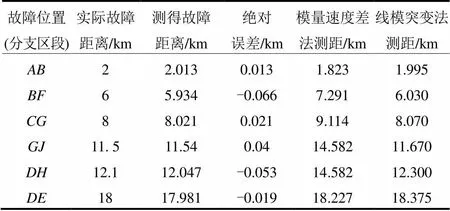
Table 1 Simulation results of different fault location

表2为只改变接地电阻时的仿真结果，故障均设置在段，距离首端9 km，故障初相角也均为90º。从表中可以看到接地电阻的变化并不影响测距的精确度，而从仿真过程中可以发现，接地电阻增大时会使首端检测到的各模行波的幅值变小，但是对各模行波第一个波头的形状基本没有影响，所以相应的小波变换的第一个模极大值点对应的时刻也没有发生变化，即测距结果不受影响。另外两种方法中，基于模量行波速度差的方法，也基本不受接地电阻的影响；而基于线模行波突变的方法则会随着接地电阻的增大而变得不精确。

表2接地电阻不同时的仿真结果

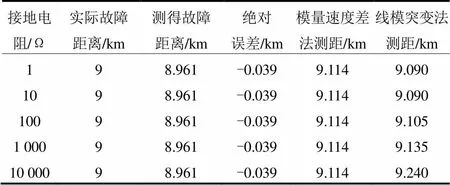
Table 2 Simulation results of different grounding resistance

表3为段中，且距离首端9 km处在不同时刻(即故障初相角不同)发生单相接地故障的仿真结果，其对应的接地电阻均为10W。从表中可知，对于不同的故障发生时刻，本方法均有较好的定位精确度。与接地电阻变化的情况类似，故障初相角主要是影响了故障产生的暂态行波的幅值大小，却并不改变各模行波第一个波头的形状，所以对测距结果基本不影响。而基于模量行波速度差的方法，由于两个模量时间差的乘积效应，使得测距结果很不稳定；基于线模行波突变的方法，由于是离线注入测距，并不受故障初相角的影响。

表3 故障初相角不同时的仿真结果

综上，本文所提的方法消除零模波速度的影响，使得在各种故障条件下的测距结果都表现得比较稳定精确。

5  结论

1) 零模行波波速度的确定是影响基于模量行波速度差和基于线模行波突变方法的测距精度的关键因素，本文提出的故障测距方法通过联合二者的测距原理，消去了零模波速度量，较大提高了测量精度。

2) 本文提出方法属单端行波测距方法，只需在首端检测行波，且只需利用小波变换识别行波各模分量的第一个波头，而不用在复杂的折反射混合波中识别第二个波头信息，避免了线路分支、分支末端等的影响。

3) 仿真验证了该方法基本不会被不同的故障位置、过渡电阻大小、故障初相角所影响，论证了方法的有效性和准确性。

[1] 唐金锐, 尹向根, 张哲, 等. 零模检测波速度的迭代提取及其在配电网单相接地故障定位中的应用[J]. 电工技术学报, 2013, 28(4): 202-211.

TANG Jinrui, YIN Xianggen, ZHANG Zhe, et al. Iterative extraction of detected zero-mode wave velocity and its application in single phase-to-ground fault location in distribution networks[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 202-211.

[2] 唐昆明, 杨伟, 张太勤, 等. 基于Stehfest 算法的配网单相接地故障双端测距方法[J]. 电力系统保护与控制, 2015, 43(14): 76-83.

TANG Kunming, YANG Wei, ZHANG Taiqin, et al. A new two-terminal fault location method for distribution network based on Stehfest algorithm[J]. Power System Protection and Control, 2015, 43(14): 76-83.

[3] 刘慧海, 张晓莉, 姜博, 等. 行波故障测距装置的检测与评价[J]. 电力系统保护与控制, 2015, 43(1): 145-149.

LIU Huihai, ZHANG Xiaoli, JIANG Bo, et al. Testing and evaluation method of fault location equipment based on traveling wave[J]. Power System Protection and Control, 2015, 43(1): 145-149.

[4] 薛永端, 徐丙垠, 李天友, 等. 配网自动化系统电 流接地故障暂态定位技术[J]. 电力自动化设备, 2013, 33(12): 27-32.

XUE Yongduan, XU Bingyin, LI Tianyou, et al. Small- current grounding fault location based on transient signals of distribution automation system[J]. Electric Power Automation Equipment, 2013, 33(12): 27-32.

[5] 牛睿, 梁军, 张峰, 等. 基于可变行波辨识时窗的单端故障定位方法[J]. 电力系统保护与控制, 2014, 42(24): 56-64.

NIU Rui, LIANG Jun, ZHANG Feng, et al. Single-ended fault location method based on variable time windows for traveling wave identification[J]. Power System Protection and Control, 2014, 42(24): 56-64.

[6] 杨炎龙. 配电网故障定位研究[D]. 广州: 华南理工大学, 2013.

[7] MORA-FLOREZ J, MELENDEZ J, CARRILLO- CAICEDO G. Comparison of impedance based fault location methods for power distribution systems[J]. Electric Power Systems Research, 2008, 78(4): 657-666.

[8] WANG Bin, DONG Xinzhou, LAN Lan, et al. Novel location algorithm for single-line-to-ground faults in transmission line with distributed parameters[J]. IET Generation Transmission & Distribution, 2013, 7(6): 560-566.

[9] 冀鲁豫. 复杂配电网故障定位方法研究[D]. 北京: 北京交通大学, 2011.

[10] 陈仕龙, 谢佳伟, 毕贵红, 等. 一种特高压直流输电线路神经网络双端故障测距新方法[J]. 电工技术学报, 2015, 30(4): 257-264.

CHEN Shilong, XIE Jiawei, BI Guihong, et al.A novel two terminal fault location method used ANN for UHVDC transmission line[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 256-264.

[11] 季涛. 基于暂态行波的配电线路故障测距研究[D]. 济南: 山东大学, 2006.

[12] 张广斌, 束洪春, 于继来, 等. 不依赖双侧时钟同步的输电线双端行波测距[J]. 电工技术学报, 2015, 30(20): 199-209.

ZHANG Guangbin, SHU Hongchun, YU Jilai, et al. Double-ended travelling wave fault location independent[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 199-209.

[13] 王阳, 曾祥军, 黎锐烽, 等. 基于图论的配电网故障行波定位新算法[J]. 电力系统自动化, 2012, 36(18): 143-147.

WANG Yang, ZENG Xiangjun, LI Ruifeng, et al. A traveling wave fault location algorithm for distribution network based on graph theory[J]. Automation of Electric Power Systems, 2012, 36(18): 143-147.

[14] 范新桥, 朱永利. 基于双端行波原理的多端输电线路故障定位新方法[J]. 电网技术, 2013, 37(1): 261-269.

FAN Xinqiao, ZHU Yongli. A novel fault location scheme for multi-terminal transmission lines based on principle of double-ended traveling wave[J]. Power System Technology, 2013, 37(1): 261-269.

[15] 朱永利, 范新桥, 尹金良. 基于三点电流测量的输电线路行波故障定位新方法[J]. 电工技术学报, 2012, 27(3): 260-269.

ZHU Yongli, FAN Xinqiao, YIN Jinliang. A new fault location scheme for transmission lines based on traveling waves of three measurements[J]. Power System Technology, 2012, 27(3): 260-269.

[16]梁睿, 靳征, 王崇林, 等. 行波时频复合分析的配电网故障定位研究[J]. 中国电机工程学报, 2013, 33(28): 130-136.

LIANG Rui, JIN Zheng, WANG Chonglin, et al. Research of fault location in distribution networks based on integration of travelling wave time and frequency analysis[J]. Proceedings of the CSEE, 2013, 33(28): 130-136.

[17] 严凤, 杨奇逊, 齐郑, 等. 基于行波理论的配电网故障定位方法的研究[J]. 中国电机工程学报, 2004, 24(9): 37-43.

YAN Feng, YANG Qixun, QI Zheng, et al. Study on fault location scheme for distribution network based on traveling wave theory[J]. Proceedings of the CSEE, 2004, 24(9): 37-43.

[18] 徐铭铭, 肖立业, 林良真. 基于零模行波衰减特性的配电线路单相接地故障测距方法[J]. 电工技术学报, 2015, 30(14): 397-404.

XU Mingming, XIAO Liye, LIN Liangzhen. A fault location method for the single-phase-to-earth fault in distribution system based on the attenuation characteristic of zero-mode traveling wave[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 397-404.

[19] 张帆, 潘贞存, 马琳琳, 等. 基于模量行波传输时间差的线路接地故障测距与保护[J]. 中国电机工程学报, 2009, 29(10): 78-83.

ZHANG Fan, PAN Zhencun, MA Linlin, et al. Transmission line fault location and protection based on the gap between zero mode and aerial mode traveling wave propagation time[J]. Proceedings of the CSEE, 2009, 29(10): 78-83.

[20] 刘朕志, 舒勤, 韩晓言, 等. 基于行波模量速度差的配电网故障测距迭代算法[J]. 电力系统保护与控制, 2015, 43(8): 88-93.

LIU Zhenzhi, SHU Qin, HAN Xiaoyan, et al. An iterative fault location algorithm using the difference of wave velocity between zero mode component and aerial mode component of traveling wave[J]. Power System Protection and Control, 2015, 43(8): 88-93.

[21] 李传兵, 谭博学, 高鹏, 等. 基于 D 型行波原理T接线路故障测距方法[J]. 电力系统保护与控制, 2013, 41(18): 78-82.

LI Chuanbing, TAN Boxue, GAO Peng, et al. A fault location method for T-connection lines based on D-type traveling wave theory[J]. Power System Protection and Control, 2013, 41(18): 78-82.

[22] 于盛楠, 杨以涵, 鲍海. 基于C型行波法的配电网故障定位的实用研究[J]. 继电器, 2007, 35(10): 1-4.

YU Shengnan, YANG Yihan, BAO Hai. Study on fault location in distribution network based on C-type travelling-wave scheme[J]. Relay, 2007, 35(10): 1-4.

[23] 周聪聪, 舒勤, 韩晓言. 基于线模行波突变的配电网单相接地故障测距方法[J]. 电网技术, 2014, 38(7): 1973-1978.

ZHOU Congcong, SHU Qin, HAN Xiaoyan. A single- phase earth fault location scheme for distribution network based on mutation of line mode traveling wave[J]. Power System Technology, 2014, 38(7): 1973-1978.

[24] 马士聪, 高厚磊, 徐丙垠, 等. 配电网故障定位技术综述[J]. 电力系统保护与控制, 2009, 37(11): 120-123.

MAO Shicong, GAO Houlei, XU Bingyin, et al. A survey of fault location methods in distribution network[J]. Power System Protection and Control, 2009, 37(11): 120-123.

[25] 施围, 郭洁. 电力系统过电压计算[M]. 2版. 北京: 高等教育出版社, 2006.

[26]梁睿, 孙式想. 单端行波故障测距的组合方法研究[J]. 电网技术, 2013, 37(3): 700-706.

LIANG Rui, SUN Shixiang. A combined method of single-ended traveling wave fault location[J]. Power System Technology, 2013, 37(3): 700-706.

[27] 覃剑, 陈祥训, 郑建超. 行波在输电线上传播的色散研究[J]. 中国电机工程学报, 1999, 19(9): 27-35.

QIN Jian, CHEN Xiangxun, ZHENG Jianchao. Study on dispersion of travelling wave in transmission line[J]. Proceedings of the CSEE, 1999, 19(9): 27-35.

[28] 李友军, 徐丽娜. 电力系统接地短路故障中零模分量的依频关系分析[J]. 继电器, 2007, 35(15): 4-8.

LI Youjun, XU Lina. Relationship between earth mode surge and frequency on power system earth fault[J]. Relay, 2007, 35(15): 4-8.

[29] 李学生, 盛洪江. 基于波速影响的零模行波研究[J]. 电力自动化设备, 2011, 31(6): 93-97.

LI Xuesheng, SHENG Hongjiang. Study of zero-mode traveling wave based on influence of wave velocity[J]. Electric Power Automation Equipment, 2011, 31(6): 93-97.

(编辑 周金梅)

A single-terminal fault location algorithm in distribution network for eliminating the effect of the velocity of zero-mode traveling wave

HE Xiao, LEI Yong, ZHOU Congcong, ZHOU Kai, WANG Peng

(School of Electrical Engineering and Information, Sichuan University, Chengdu 610065, China)

Due to frequently occurred three-phase unbalanced loads in the ends of large number of branches in distribution networks, it is difficult to extract reflected wave of the fault point in the complex reflected and refracted waves using the traditional single-terminal traveling wave methods. Simultaneously the precision of the fault location methods based on the difference of wave velocity between zero-mode component and line-mode component of traveling waves and the one based on mutation of line-mode traveling wave are decided by the unstable zero-mode wave velocity. Therefore, a new approach is proposed by combining the above two methods to achieve higher efficiency and precision of measuring the fault distance and location. The presented method employs the correspondence between the detected zero-mode wave velocity and the fault distance to achieve the fault location algorithm which is not impacted by zero-mode wave velocity. The approach firstly detects difference of arrival time between the zero-mode traveling wave and line-mode traveling wave at the head end. And then post-injecting high voltage pulses into three phases simultaneously and detecting the arrival time of the first line-mode traveling wave head at the head end of the transmission line. Following, it employs the stable line-mode wave velocity to execute the measurement of the fault distance. Finally, PSCAD-based simulation shows that the absolute errors of this algorithm are less than 100 m in all cases, without influence from the fault location, grounding resistance and fault initial phase angle.

This work is supported by National Natural Science Foundation of China (No. 51407121).

distribution network; fault location; zero-mode traveling wave; wavelet transform; wave head

10.7667/PSPC152169

2015-12-14；

2016-03-28

何 晓( 1991-)，女，硕士研究生，研究方向为电力设备故障点检测与定位；E-mail: xiao_he1008@163.com

雷 勇(1966-)，男，博士，教授，研究方向为电工理论与新技术、智能电网状态监测与控制、机器人等；E-mail: 420974017@qq.com

周聪聪(1989-)，男，硕士研究生，研究方向为配电网故障定位和电力系统信号检测与处理。E-mail: zhoucongcong89@qq.com

国家自然科学基金青年基金(51407121)