基于混沌理论与改进回声状态网络的网络流量多步预测

田中大，李树江，王艳红，王向东



基于混沌理论与改进回声状态网络的网络流量多步预测

田中大，李树江，王艳红，王向东

（沈阳工业大学信息科学与工程学院，辽宁沈阳 110870）

网络流量预测是网络管理及网络拥塞控制的重要问题，针对该问题提出一种基于混沌理论与改进回声状态网络的网络流量预测方法。首先利用0-1混沌测试法与最大Lyapunov指数法对不同时间尺度下的网络流量样本数据进行分析，确定网络流量在不同时间尺度下都具有混沌特性。将相空间重构技术引入网络流量预测，通过C-C方法确定延迟时间，G-P算法确定嵌入维数。对网络流量时间序列进行相空间重构之后，利用一种改进的回声状态网络进行网络流量的多步预测。提出一种改进的和声搜索优化算法对回声状态网络的相关参数进行优化以提高预测精度。利用网络流量的公共数据集以及实际数据进行了仿真，结果表明，提出的预测方法具有更高的预测精度以及更小的预测误差。

网络流量；混沌；回声状态网络；时间尺度；预测

1 引言

随着网络技术的发展，网络规模越来越大和复杂化，网络信息流量剧增，网络拥塞越来越严重，网络管理的难度日益增加，如何有效地管理和控制网络，为用户提高更加优质服务显得十分重要。网络流量是衡量网络运行负荷和状态的重要参数，通过对网络流量的监测，可以及时了解网络当前运行状况，因此如何进行网络流量的精确预测引起了学者广泛的关注[1]。

网络流量是一定采样时间内通过网络设备或传输介质的信息量(报文数、数据分组数或字节数)。一般的研究对象都为基于IP协议的网络流量。网络流量预测问题可定义为[2]：给定当前时刻的一组IP网络流量数据，则未来某一时刻的流量可由给出，这里为预测步长。当时为单步预测，时为多步预测。相对于单步预测而言，多步预测有着更重要的理论与实际意义。

网络流量是按时间采集的，因此是一种典型的时间序列数据，具有高度非线性、多时间尺度和不确定性等特点。近些年来，诸多学者对网络流量预测进行研究，提出了许多的预测方法。其中，很多学者将网络流量看作线性模型，采用自回归滑动平均(ARMA, auto regressive moving average)模型[3, 4]、差分自回归滑动平均(ARIMA, auto regressive integrated moving average)模型[5, 6]以及差分自回归求和滑动平均模型[7,8](FARIMA, fractional auto regressive integrated moving average)等线性模型进行预测。但是随着网络复杂度的增加，网络流量特性已经超出传统意义上认为的泊松或者马尔可夫分布模型，而这些传统时间序列分析方法均属于线性模型，适合于季节性、周期性等特征平稳的时间序列预测。对于具有非平稳、非线性特征的网络流量时间序列，由于它们不能全面反映网络流量序列的复杂变化特征，预测准确率比较低，使预测的精确性无法提高。而非线性预测模型主要包括支持向量机[9,10]（SVM, support vector machine）、最小二乘支持向量机[11,12]（LSSVM, least squares support vector machine）、人工神经网络（RBF神经网络[13]、ELM神经网络[14]以及Elman神经网络[15]等）、卡尔曼滤波模型[16](KFM, Kalman filtering mode)、灰色模型[17]等。虽然非线性模型的预测精度较线性模型有了一定程度的提高，但是也存在着各自的缺陷。SVM与LSSVM虽然需要样本数少，但是其关键参数很难确定，预测精度受核参数影响很大；神经网络虽然可以任意精度逼近非线性函数，但是其存在易陷于局部最优值、网络结构难以确定的缺点；卡尔曼滤波模型误差难以量化，而网络流量具有随机性和突发性，使KFM模型运算量大，参数设置复杂，实际应用性较差；灰色模型只适合网络流量数据变化不是剧烈的情况下。因此网络流量的非线性预测模型也都存在着各自的局限性。很多学者也提出了一些混合预测模型[18~20]，即将2种以上的预测模型通过某些算法进行结合，达到提高预测精度的目的。

虽然学者们在网络流量预测问题上进行了大量的研究，但是目前的研究大多未考虑网络流量时间序列具有的混沌特性，而实际网络是一个时变的、开放的复杂巨系统，因此网络流量具有高度的非线性和不确定性。理论上更精确的预测方法是用符合网络流量特性的非线性动力学理论进行建模并预测，以提高预测精度和可信度。对于确定性混沌系统，采用基于混沌的相关理论进行预测，就能获得较高的预测精度。但是目前考虑到混沌特性的相关研究只针对单一时间尺度的网络流量进行预测[21,22]。因而确定不同时间尺度下网络流量序列是否具有混沌特性，是应用混沌理论进行网络流量预测的前提。基于以上考虑，首先对不同时间尺度的网络流量时间序列进行混沌特性分析，通过0-1混沌测试法与最大Lyapunov指数法确定网络流量时间序列具有混沌特性。针对网络流量时间序列的混沌特性结合相空间重构技术展开预测，利用C-C方法确定序列延迟时间，通过G-P算法确定序列嵌入维数。

在预测模型的选择上，利用Jaeger等[23]于2001年提出的一种新型的递归神经网络—回声状态网络(ESN, echo state network)。ESN核心部分是一个大规模储备池，网络的输入权值和储备池内部连接权值随机生成，并在训练中保持不变，只有输出权值需要通过线性回归方法求解，学习算法简单快速，弥补了一般神经网络收敛速度慢的缺点。为了克服不同的储备池参数以及输入数据噪声对于ESN预测效果的影响，提出对ESN输入端加入补偿信号与比例系数，同时利用改进的和声搜索算法完成ESN最佳预测参数的确定。

综上所述，本文提出一种基于混沌理论与回声状态网络的网络流量多步预测方法，首先确定网络流量时间序列具有混沌特性，对原始网络流量进行相空间重构处理，然后通过改进的和声搜索算法优化预测模型的相关参数，利用优化后的参数进行网络流量的多步预测。通过仿真实验表明提出的方法具有更高的预测精度与更小的预测误差。

2 网络流量数据来源及其分形特征

网络流量数据分组包括公共数据集与实际数据2部分。网络流量时间尺度的划分基本上分为小时间尺度与大时间尺度。一般认为小时间尺度为采样时间小于1 s。因此本文也认为采样间隔在1 s以内的为小时间尺度，大于1 s间隔的为大时间尺度。

小时间尺度网络流量数据集来自于http://ita.ee. lbl.gov/html/contrib/BC.html中的BC-pAug89数据集，其采集了3 142.82 s内的包括局域网、广域网等网络的单向流量，按照10 ms、100 ms、1 s的采样间隔，将数据集分成T_10 ms、T_100 ms、T_1s这3个数据集，为了对比研究方便，数据集长度均取为1 000。大尺度网络流量数据为ftp://ita.ee. lbl.gov/traces/BC-Oct89Ext4.TL.Z中的BC-Oct89Ext4数据集，共采集了307 h的共106组网络流量数据。对其按照10 s、1 min、10 min、30 min、1 h的间隔采样，生成T_10s、T_1min、T_10min、T_30min、T_1hour 5个数据集，这里前6个数据集的长度都取为1 000，后2个数据集长度取为300。8个数据集数据传输层均采用TCP协议，数据集的单位为byte。由此得到的8个数据集如图1所示。

实际网络流量数据来源于中国联合网络通信公司辽宁分公司3G网络一核心路由器流入的网络流量数据，数据采集尺度为10 min，传输层协议为TCP协议，共采集300组数据，单位为MB。图2为300组实际网络流量数据。

在给出网络流量数据来源后，这里将对网络流量数据进行分形特征的讨论。分形理论由美国科学家Benoit于20世纪70年代中期创立，分形理论用于研究复杂系统的自相似性。重标度极差分析(R/S, rescaled range analysis)是以分形理论为基础的时间序列研究方法，该方法特别适用于分析具有长相关特性的非线性时间序列，而且对所研究对象可不做任何假设，属非参数分析法，具有较好的稳健性[24]。1951年，英国学者Hurst在研究尼罗河水流量时，提出了R/S分析方法建立Hurst指数，作为判断时间序列数据是否是随机游走还是有偏随机游走的指标。随后分形学说创始人Mandelbort在理论上证实了该方法的正确性，并加以完善与补充[25]。其方法可描述为

图1 不同时间尺度下的网络流量序列

表1 不同时间尺度网络流量的Hurst指数

从表1中可观察到，不同时间尺度下的网络流量时间序列具有分形特征，且Hurst 指数值均大于0.5，表明不同时间尺度下的网络流量时间序列数据服从分形布朗运动，且时间序列具有长期的正相关特征，所测定的时间周期内表现的特征将得到延续，即趋势具有可持续性，这也说明了网络流量时间序列的可预测性。

3 网络流量时间序列混沌特性与相空间重构

混沌现象是非线性动力系统中常见的现象。混沌系统是一个确定系统，它对系统初值具有较强的敏感性。对于混沌系统的预测而言，由于其存在初值敏感性，因此不能长期预测，但是同时由于其确定性，混沌系统具有短期预测能力。对于网络流量时间序列的预测问题，首先需要确定其是否具有混沌特性，只有进行不同时间尺度下网络流量时间序列的混沌特性判定，才能确定不同时间尺度下网络流量时间序列的可预测性。

网络流量时间序列的混沌特性判定可通过0-1混沌测试方法[26]与最大Lyapunov指数[27]2种方法。受限于篇幅，算法具体计算过程可参见相关文献。

3.1 0-1混沌测试法

从图3~图5可看出，10 ms时间尺度网络流量时间序列的与的相图呈现布朗特性，而均方位移随时间线性增长，同时计算可得到渐进增长率K为0.998 3，接近于1，因此10 ms时间尺度网络流量序列具有混沌特性。同理，对其余8个不同时间尺度的网络流量时间序列计算其渐进增长率，结果如表2所示，从中可看出不同时间尺度下的都趋近于1，0-1混沌测试法表明网络流量时间序列在不同时间尺度下都具有混沌特性。

表2 不同时间尺度网络流量的渐进增长率

3.2 相空间重构

相空间重构是混沌时间序列预测的基础，相空间重构用原始系统中某个变量的延迟坐标来重构相空间，Takens从数学上为其奠定了可靠的基础。他的基本观点是：相空间重构法虽然是用一个变量在不同时刻的值构成相空间，但动力系统的一个变量的变化自然跟此变量与系统的其他变量的相互作用有关，即此变量随时间的变化隐含着整个系统的动力学规律。因此，重构的相空间的轨迹也反映系统状态的演化规律。

受限于篇幅，这里仅对10 ms时间尺度网络流量时间序列进行详细分析。利用C-C算法得到10 ms网络流量时间序列的变化曲线如图6所示。从图中可看出的第一个局部最小值发生在，因此确定10 ms时间尺度网络流量时间序列的时延为2。按照G-P算法得到图7所示的随着的增大，的变化曲线，图8的与关联维数的曲线。从图7与图8可知，随着嵌入维数的增加，线性区域内出现了趋于饱和的现象，继续增加嵌入维数几乎不影响关联积分的值。从图8中可看出关联维数的收敛值为4.5左右，依据原则，确定10 ms时间尺度网络流量时间序列的嵌入维数为10。

对于一个混沌时间序列，如果延迟时间取值不合理，混沌吸引子的相轨线被压缩或被折叠，空间点对的距离分布不均匀。而从图9与图10的相图可看出在为2时，空间点对点间的距离趋于均匀分布，吸引子所包含信息量较大，二维与三维相图表明其对吸引子有序结构的展开相对较为充分，因此确定延迟时间为2较为合理。

将10 ms时间尺度网络流量时间序列按照得到的嵌入维数与延迟时间进行相空间重构，计算其递归图（RP, recurrence plot），结果如图11所示。

图11表明，10 ms时间尺度网络流量时间序列不同于随机信号，其递归图并非均匀分布于整个递归平面，而且存在与主对角线平行的直线段，因此10 ms尺度网络流量序列为典型的混沌时间序列，在局部范围内具有可预测性。同理，可计算其他时间尺度网络流量时间序列对应的相空间参数，结果如表3所示。

表3 不同时间尺度网络流量时间序列相空间参数

3.3 最大Lyapunov指数

Lyapunov指数描述了系统轨道演化过程的特性，度量了系统对于初始条件依赖的敏感性，通过其各指数符号组合能很好判断出系统的最终演化是否会出现混沌现象，Lyapunov指数中，最大的指数非常重要，如果网络流量系统是混沌的，则至少有一个正的Lyapunov指数。利用wolf方法计算了9个数据集的最大Lyapunov指数，结果如表4所示。从表4中可发现9个数据集的最大Lyapunov指数都大于0，因此同样可表明网络流量时间序列同样具有混沌特性。

表4 不同时间尺度网络流量的最大Lyapunov指数

通过0-1混沌测试法与最大Lyapunov指数方法可知网络流量时间序列具有混沌特性，同时利用混沌理论中的相空间技术得到各个时间尺度网络流量序列的重构参数后，将利用下节的回声状态网络进行网络流量的预测。

4 回声状态网络

回声状态网络将网络隐层设计成一个具有很多神经元组成的稀疏网络，通过调整网络内部权值的特性达到记忆数据的功能。其内部的动态储备池(DR, dynamic reservoir)包含了大量稀疏连接的神经元，蕴含系统的运行状态，并具有短期记忆功能,而非线性系统的动态特性即由DR产生。回声状态网络一经提出便成为学术界的研究热点，并应用到各种不同领域，尤其是时间序列的预测问题[33~35]。图12为ESN网络结构[36]。

4.1 ESN学习算法

设系统具有个输入单元，个内部处理单元，同时具有个输出单元，输入单元、内部状态、输出单元在时刻的值分别为

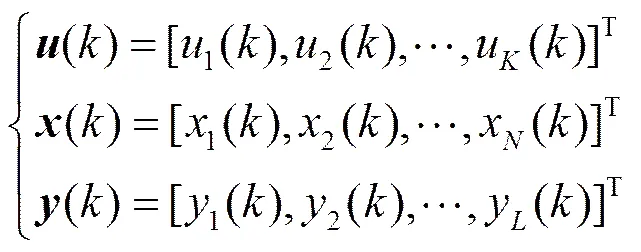
与传统神经网络相比，ESN的隐层是由较多神经元构成的循环网络所形成的动态储备池。为使DR内部具有动态记忆能力，权值通常保持连接度5%至10%，谱半径小于1。

(4)

4.2 权值计算

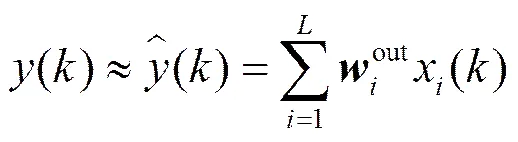
也就是希望计算权值矩阵满足系统均方误差最小，即求解如下目标

(6)

可归结为如下形式

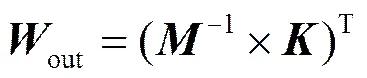
4.3 基于相空间重构与ESN的网络流量多步预测

本文使用迭代法实现基于相空间重构与ESN的网络流量多步预测，即ESN输出层为1，通过反复迭代完成多步预测，其实现步骤可表示为如下。

step1 采集网络流量数据，假设目前采集得到的网络流量时间序列为，利用C-C方法计算延迟时间，利用G-P算法计算嵌入维数，生成相空间重构参数。

step2 对ESN模型参数赋值。生成输入输出集合，对ESN进行训练，生成对应权值矩阵。

5 改进的ESN及储备池参数优化

5.1 储备池参数优化

ESN的性能由储备池的4个参数决定的，简要介绍储备池的4个参数[37]。

1) 储备池内部连接权谱半径。为连接权矩阵的绝对值最大的特征值，记为，是保证网络稳定的必要条件。合理的才能确保ESN具有的回声状态属性，使网络状态与输入在足够长的时间后，对网络的影响消失。

2) 储备池规模。为储备池中神经元的个数，储备池的规模选择与样本个数有关，对网络性能影响很大，储备池越大ESN对给定动态系统的描述越准确，但是过大会带来过拟合问题，导致模型对测试数据的泛化能力下降，目前一般的方法是逐渐增大，直到测试数据的性能指标变坏为止。

3) 储备池输入单元尺度。为储备池的输入信号连接到储备池内部神经元之前需要相乘的一个尺度因子，即对输入信号进行一定的缩放。Jaeger在其文献[23]中给出了选择原则，即需要处理的对象非线性越强，越大。其本质是通过，将输入数据转换到神经元激活函数所能适应的范围。

4) 储备池稀疏程度。表示储备池中神经元之间的连接情况，储备池中并不是所有神经元之间都存在连接的。表示储备池中相互连接的神经元占总的神经元（）的百分比。可以衡量储备池所包含向量的丰富程度，向量的丰富程度影响网络的非线性逼近能力，因此越大意味着网络非线性逼近能力越强。

储备池的参数对于ESN网络流量预测模型的预测精度有着重要的影响，为了说明这些参数对预测精度的影响，以10 ms时间尺度网络流量序列为例，利用前400组数据作为输入，401到500组作为输出进行了测试。图13给出了嵌入维数，输入单元尺度，储备池稀疏程度，谱半径变化范围为[0.1,1)，变化步长为0.05，储备池规模变化范围为[10,150)，变化步长为1，100组网络流量预测值与实际值之间均方根误差（RMSE）的分布。

从图13与图14可以看出储备池参数对于预测精度会造成不同的影响，因此如何根据网络流量训练集选择合适的模型参数是一个重要的问题，直接影响最后ESN预测的精度。为了得到最优的储备池参数，提出一种改进的和声搜索算法（IHS）进行储备池参数的寻优。

和声搜索（HS, harmony search）算法是2001年源于乐曲创作过程的模仿而出现的群智能优化算法[38]，算法利用所有个体的合作而产生新个体，具有不依赖初始条件，结构简单、实现容易、收敛速度快等特点[39]，相关文献[40, 41]表明和声搜索算法的优化性能要强于遗传、模拟退火、粒子群等优化算法。

如下为标准HS算法实现步骤。给定优化问题

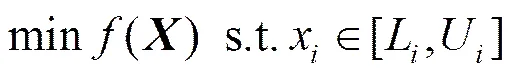
step1 HS算法首先初始化如下参数：和声记忆库大小（HMS, harmony memory size）、学习与记忆库概率（HMCR, harmony memory consideration rate）、微调概率（PAR, pitch adjusting rate）、音调微调带宽（BW, band width）、迭代次数（NI, number of iteration）。

step2 随机创建和声记忆库如下

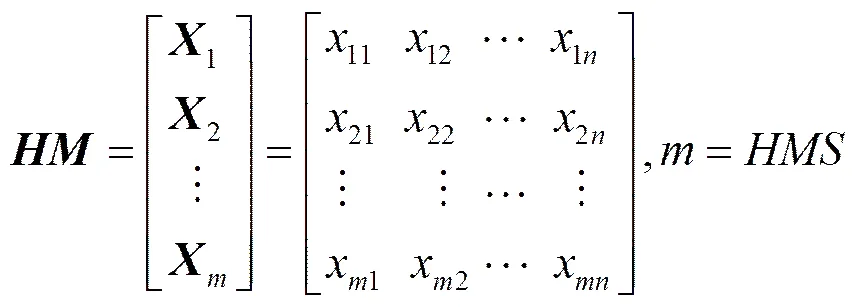
(9)

(10)

step5 重复步骤step3和step4，直到迭代次数达到。

虽然和声搜索算法具有较好的全局寻优能力，但是其算法存在随机性大，稳定性不高，同时搜索没有方向性，因此在此作一定的改进。由基本和声搜索算法描述可知，HMCR有助于算法找到全局改进解和局部改进解，而PAR和BW在和声微调中是非常重要的2个参数，优化前期阶段保持较小的PAR值与较大的BW值有利于增强解向量的多样性，从而能快速找到局部最优解。而在优化的后期，较小的BW与较大的PAR值有利于算法快速找到全局最优解。标准的和声搜索算法采用了固定的参数值，不能同时兼顾局部最优解和全局最优解的要求。同时算法的搜索速度与收敛精度也和算法参数是相关的，为提高算法搜索效率，克服标准和声搜索算法的缺点，作如下的改进。

对于参数HMCR应由大到小动态调节，这样可使HM算法先对和声记忆库内充分搜索，迭代搜索后期转到和声记忆库外部搜索，可提高种群的多样性，调节方法如下。

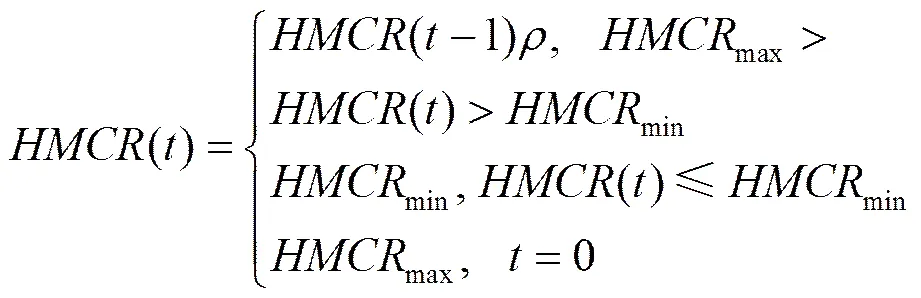
在HS算法的初期，PAR取值小有利于算法快速的搜索更好的区域，在HS算法的后期，较大的PAR则利于算法跳出局部最优值，因此PAR应该是从小到大变化的，改进的PAR变化策略如下

(12)

对于BW，在算法初期较大的BW有利于HS算法在较大的范围内搜索，而算法搜索后期，较小的BW则有利于小范围内的精确搜索，因此BW应该由大变小的，改进的BW的变化策略如下。

(14)

为了验证改进HS算法（IHS, improved harmony search）的性能，选用式（15）的Rosenbrock函数进行测试。

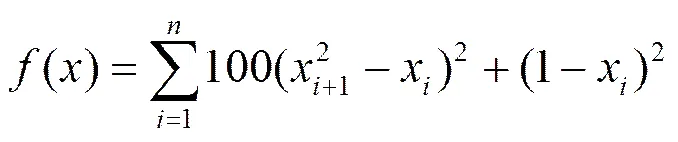
为了消除随机性的影响，所有算法都运行20次，取平均值作为寻优结果，图15为某一次测试3种算法的适应度收敛曲线，为了显示方便，横坐标为每迭代50次记录一次适应度值，纵坐标为适应度取10的对数值，从图中可看出本文改进的HS算法较标准HS算法以及EHS算法收敛速度更快，同时具有更好的适应度值。表5给出了3种算法的最佳适应度值，平均适应度值，适应度均值的对比，最佳适应度值与平均适应度值反映了算法的收敛性，适应度均值反映了算法的顽健性，成功率反映了算法全局寻优能力。从表中可看出本文方法的最佳适应度、适应度均值等指标都优于其他2种算法。

表5 算法仿真结果

5.2 改进的ESN

虽然利用上节的IHS算法可以对ESN的储备池参数进行优化，但是ESN的性能与网络输入数据也是相关的，尤其输入数据中的噪声对于预测性能有着一定的影响。为了消除输入数据中的噪声信号，可在输入端加入一个补偿信号，则式（3）转变为

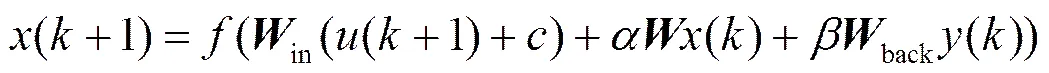
(17)

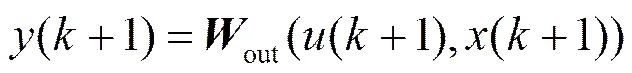
相较于标准ESN，改进的ESN由于引入输入的补偿而增加了3个参数、与，为了统一处理，这里可以同样采用上节的IHS算法进行优化。

这里对改进的ESN进行算法稳定性分析。文献[43]指出只有网络具有回声状态属性时，对网络的训练才是有意义的，因此网络的训练算法应该保证网络具有回声状态属性。通过对随机产生的内部连接权矩阵进行整体的运算保证储备池的回声状态属性，即保证网络的稳定性。实际应用中在稳定性方面，它可以通过预先设定动态记忆库矩阵的谱半径来保证递归网络的稳定性,当矩阵的谱半径小于1（）时，回声状态网络是渐进稳定的，由于本文并未改进标准ESN权值矩阵的产生过程，因此改进的ESN也是渐进稳定的。

综上，基于改进的ESN与储备池参数优化的预测过程可描述如下。

1) 建模过程

step1 采集网络流量数据，生成建模数据集。

step2 根据网络流量训练样本序列，通过C-C算法与G-P算法确定相空间重构参数。

step3 设置IHS算法参数，设定待优化参数为储备池参数、、、以及、与取值范围。

step4 网络流量样本数据归一化处理，利用相应样本参数训练ESN，将网络流量预测值与网络流量实际值的RMSE作为适应度函数，即

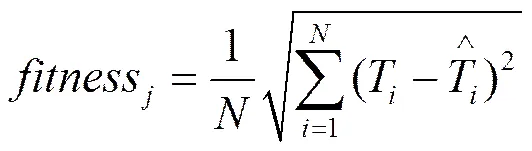
利用IHS算法结合适应度函数反复迭代进行参数的优化，直到满足结束条件，输出最佳参数。

2) 在线预测过程

step2 按照式（6）、式（7）进行网络训练，计算输出权矩阵，通过式（17）、式（18）预测未来时刻的网络流量预测值。

6 仿真对比

为了说明本文方法的有效性，利用10 ms时间尺度网络流量时间序列与实际采集的辽宁联通网络流量时间序列进行仿真研究。其中10 ms时间尺度网络流量序列前400组数据作为训练样本，401到500组作为测试样本。辽宁联通网络流量样本数据前250组作为训练样本，后50组作为测试样本。储备池参数的变化范围为，，，。由于网络流量数据都进行了归一化处理，因此改进ESN的3个参数取值范围为，，。按照上文步骤利用IHS算法进行参数优化，优化结果如表6所示。

表6 参数优化结果

预测精度是指预测模型对实际数据拟合的好坏程度，即预测模型所产生的预测值与实际值拟合程度的优劣。除了通过预测曲线拟合程度之外，预测效果的评价指标还包括MAE（平均绝对误差）、MAPE（平均绝对百分误差）、RMSE（均方根误差）、ME（绝对误差）、MRE（平均相对误差）等。MAE、MAPE以及RMSE对较大的预测误差不存在正负抵消的问题，易于计算，对于预测系统的整体性能评价十分重要，而ME与MRE等评价指标由于将正误差与负误差正负抵消，会导致对预测效果的错误判断，因此选择MAE、MAPE与RMSE作为评价指标。RMSE定义如式（19），MAE与MAPE的定义分别如式（20）与式（21）。

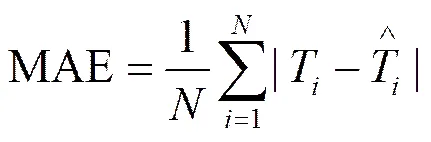
(21)

6.1 T_10ms数据集仿真对比

作为对比，与文献[3]中的ARMA模型（预测模型参数为=3,=1），文献[4]中的ARIMA模型（预测模型参数为=4,=3,=1），文献[12]中的组合核函数LSSVM模型（预测模型参数为=32，=0.92，=101.36，=6.21，=3.25），文献[15]中的Elman神经网络(预测模型参数为输入层为300，中间层为50，输出层为100，最大迭代次数为5 000)进行了仿真对比。图16为本文预测方法与其他几种方法的网络流量预测值与实际值对比曲线，图17为几种方法的预测误差分布对比。从图16与图17可知提出的预测方法具有更好的预测效果与预测精度，预测误差更小，预测值与实际值拟合更好。

表7为本文方法与其他几种方法的T_10ms数据集预测评价指标的对比。

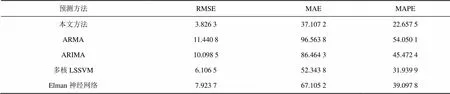
表7 T_10ms数据集预测指标对比

从10 ms时间尺度的网络流量预测仿真结果中可看出，本文的网络流量预测方法在数据拟合程度以及预测误差上都优于当前主要的预测方法。对于其他时间尺度的7组网络流量也进行了仿真验证，预测效果与精度同样优于其他的方法，限于篇幅原因，这里不给出具体仿真结果。

对于时间序列预测问题，预测时间也是一个重要的指标。预测时间包括离线建模时间与在线预测时间。表8为本机（CPU为Intel i3-4030, 4 GB内存，Windows 7操作系统，仿真软件Matlab R2010b）环境下的建模与100步在线预测所需时间。从表8中可看出，由于本文需要利用IHS算法对ESN的参数进行优化建模，因此需要的时间要长于ARMA、ARIMA以及Elman神经网络，与多核LSSVM比较接近。这些模型在线预测时间相差不大，各个模型的单步预测时间都小于采样周期10 ms，说明这些预测方法都可以满足T_10ms数据集，而对于更大时间尺度的100 ms甚至秒级之上的网络流量而言，在线预测时间远小于其时间尺度，因此在线预测时间可满足实际的应用。

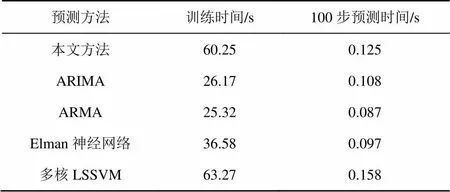
表8 不同模型离线建模与在线预测时间对比

6.2 联通网络流量数据集仿真对比

对比模型依然选择上节的几种预测方法，ARMA模型参数为=7,=6；ARIMA模型参数为=9，=8,=1；组合核函数LSSVM模型参数同文献[12]；Elman神经网络参数为输入层为150，中间层为80，输出层为50，最大迭代次数为5 000。图18为本文预测方法与其他几种方法的网络流量预测值与实际值对比曲线，图19为几种方法的预测误差分布对比，表9为几种方法的联通网络流量数据集预测评价指标的对比。

从图18、图19以及表9可知提出的预测方法对于实际采集的网络流量数据同样具有更好的预测效果。

表9 联通网络流量数据集预测指标对比

基于以上仿真结果，预测效果提高的主要原因在于通过0-1混沌测试法与最大Lyapunov指数法确定网络流量具有混沌特性，将相空间重构技术引入网络流量预测，同时对ESN进行一定的改进，并结合IHS算法进行储备池参数的联合优化，因此提高了网络流量的预测精度。

7 结束语

针对网络流量的预测问题而提出一种基于混沌理论与回声状态网络的网络流量多步预测方法。首先将网络流量样本按照不同时间尺度进行分类，通过0-1混沌测试法与最大Lyapunov指数法对不同时间尺度网络流量进行分析，确定网络流量具有混沌特性。在此基础上，利用相空间重构技术，确定重构参数，然后通过改进的回声状态网络对网络流量进行多步预测。同时，利用改进的和声搜索算法对回声状态网络预测模型相关的参数进行优化。通过仿真对比表明所提出的预测方法具有更高的预测精度以及更小的预测误差。

[1] QU H, MA W T, ZHAO J H. Prediction method for network traffic based on maximum correntropy criterion[J]. China Communications, 2013(1):134-145.

[2] 王升辉, 裘正定. 结合多重分形的网络流量非线性预测[J]. 通信学报，2007, 28(2):45-50.

WANG S H, QIU Z D. Network traffic nonlinear prediction combined with mutifractal[J]. Journal on Communications，2007, 28(2): 45-50.

[3] LANER M, SVOBODA P, RUPP M. Parsimonious fitting of long-range dependent network traffic using ARMA models[J]. IEEE Communications Letters，2013，17(12): 2368-2371.

[4] ZHOU D D, CHEN S L, DONG S. Network traffic prediction based on ARIMA model[J]. International Journal of Computer Science Issues, 2012,6(9):106-111.

[5] WANG J. A process level network traffic prediction algorithm based on ARIMA model in smart substation[C]// 2013 IEEE Int Conf on Signal Processing, Communications and Computing. Washington, DC. c2013: 1-5.

[6] 袁小坊，陈楠楠，王东，等. 城域网应用层流量预测模型[J]. 计算机研究与发展, 2009, 46(3): 434-442.

YUAN X F, CHEN N N, WANG D，et al. Traffic prediction models of traffics at application layer in metro area network[J]. Journal of Computer Research and Development, 2009, 46(3):434-442.

[7] REN X Y，YANG Y，ZHANG J F, et al. Parameter estimation and application of time-varying FARIMA model[J]. International Journal of Advancements in Computing Technology, 2011, 3(3):89-94.

[8] 陈晓天, 刘静娴. 改进的基于小波变换和FARIMA 模型的网络流量预测算法[J]. 通信学报, 2011, 32(4): 153-157.

CHEN X T, LIU J X. Network traffic prediction based on wavelet transformation and FARIMA[J].Journal on Communications,2011, 2011, 32(4): 153-157.

[9] 孟庆芳, 陈月辉, 冯志全. 基于局域相关向量机回归模型的小尺度网络流量的非线性预测[J]. 物理学报，2013,62(15):150509.

MENG Q F, CHEN Y H, FENG Z Q, et al. Nonlinear prediction of small scale network traffic based on local relevance vector machine regression model[J]. Acta Phys Sin, 2013, 62(15):150509.

[10] LIU X W, LI H, CHEN L. An improved forecasting algorithm for wireless network traffic[J]. IEICE Electronics Express, 2011, 8(12):916-922.

[11] 唐舟进, 彭涛, 王文博.一种基于相关分析的局域最小二乘支持向量机小尺度网络流量预测算法[J]. 物理学报，2014,63(13):130504.

TANG Z J, PENG T, WANG W B. A local least square support vector machine prediction algorithm of small scale network traffic based on correlation analysis[J]. Acta Phys Sin, 2014,63(13):130504.

[12] 田中大，高宪文，石彤. 用于混沌时间序列预测的组合核函数最小二乘支持向量机[J]. 物理学报，2014,63(16)：160508.

TIAN Z D, GAO X W, SHI T. Combination kernel function least squares support vector machine for chaotic time series prediction[J]. Acta Phys Sin, 2014, 63(16)：160508.

[13] Li X B. RBF neural network optimized by particle swarm optimization for forecasting urban traffic flow[C]// 3rd International Symposium on Intelligent Information Technology Application. c2009: 124-127.

[14] QIAN F. A extreme learning machines approach for accurate estimation of large-scale IP network traffic matrix[J]. Journal of Computational Information Systems, 2012, 8(2):755-762.

[15] WANG J S, WANG J K, ZHANG M Z. Prediction of internet traffic based on Elman neural network[C]// Chinese Control and Decision Conference. c2009: 1248-1252.

[16] 赵艳平，姜子运. 基于EKF的神经网络在网络流量预测中的应用[J]. 兰州交通大学学报，2009, 28(6)：23-25.

ZHAO Y P, JIANG Z Y. Network traffic prediction based on EKF neural network[J]. Journal of Lanzhou Jiaotong University, 2009, 28(6)：23-25.

[17] CAO J H, LIU Y, DAI Y. Network traffic prediction based on error advanced DGM(1,1) model[C]// International Conference on Wireless Communication Networking and Mobile Computing. c2007:6353-6356.

[18] PENG Y, LEI M, LI J B, et al.A novel hybridization of echo state networks and multiplicative seasonal ARIMA model for mobile communication traffic series forecasting[J]. Neural Computing and Applications, 2012: 1-8.

[19] WANG P, ZHANG S Y, CHEN X J. VoIP traffic capacity estimation of hybrid network based on finite user timely refuse model[C]// 5th International Conference on Wireless Communications, Networking and Mobile Computing. c2009:1-4.

[20] CHANG B R, TSAI H F. Improving network traffic analysis by foreseeing data-packet-flow with hybrid fuzzy-based model prediction[J]. Expert Systems with Applications, 2009, 36(2): 6960-6965.

[21] 温祥西，孟相如，马志强，等.小时间尺度网络流量混沌性分析及趋势预测[J]. 电子学报,2012, 40(8): 1609-1616.

WEN X X, MENG X R, MA Z Q , et al. The chaotic analysis and trend prediction on small-time scale network traffic[J]. Acta Electronic Sinica, 2012, 40(8): 1609-1616.

[22] LIU X W, FANG X M，QIN Z H，et al. A short-term forecasting algorithm for network traffic based on chaos theory and SVM[J]. Journal of Network and Systems Management, 2011, 19(4): 427-447.

[23] JAEGER H, HAAS H. Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication[J]. Science, 2004, 304(5667): 78-80.

[24] XUE Y, JIA L S, TENG W Z, et al. Long-range correlations in vehicular traffic flow studied in the framework of Kerner's three-phase theory based on rescaled range analysis[J]. Communications in Nonlinear Science and Numerical Simulation, 2015, 22(1-3): 285-296.

[25] MANDELBORT B B. How long is the coast of Britain statistical self-similarity and fractional dimension[J]. Science, 1967, 1556(3775):636-678.

[26] GOTTALD G A, MELBOURNE I. On the implementation of 0-1 test for chaos[J]. SIAM Journal on Applied Dynamical Systems, 2009, 8(1):129-145.

[27] WOLF A, SWIFT J B, SWINNEY H L, et al. Determining Lyapunov exponents from a time series[J]. Physica D, 1985, 16:285-317.

[28] 李新杰, 胡铁松, 等. 0-1测试方法的径流时间序列混沌特性应用[J]. 水科学进展，2012, 32(6): 875-882.

LI X J, HU T S, et al. Application of the 0-1 test algorithm for chaos to runoff time series[J]. Advances in Water Science, 2012, 32(6): 875-882.

[29] KHATIBI R，SIVAKUMAR B，GHORBANI M A，et al . Investigating chaos in river stage and discharge time series[J].Journal of Hydrology，2012（414-415）：108-117.

[30] KIM H S, EYKHOLT R, SALAS J D. Nonlinear dynamics delay times, and embedding windows [J]. Physica D, 1999, 127(1): 48-60.

[31] 张洪宾,孙小端,贺玉龙.短时交通流复杂动力学特性分析及预测[J]. 物理学报，2014,63(4):040505.

ZHANG H B, SUN X D, HE Y L. Analysis and prediction of complex dynamical characteristics of short-term traffc flow[J]. Acta Phys. Sin, 2014,63(4): 040505.

[32] GRASSBERGER P, PROCACCIA I. Measuring the strangeness of strange attractors[J]. Physics D, 1983, 9:189-208

[33] ONGENAE F, VAN L S, VERSTRAETEN D, et al. Time series classification for the prediction of dialysis in critically ill patients using echo state networks[J]. Engineering Applications of Artificial Intelligence, 2013,26(3):984- 996.

[34] SHENG C Y, ZHAO J, LIU Y，et al. Prediction for noisy nonlinear time series by echo state network based on dual estimation[J]. Neurocomputing,2012(82):186-195.

[35] LI D C，HAN M，WANG J. Chaotic time series prediction based on a novel robust echo state network[J]. IEEE Trans on Neural Networks and Learning Systems，2012,23（5）：787-797.

[36] OZTURK M C, XU D M, PRINCIPE J C. Analysis and design of echo state networks[J]. Neural Computation, 2007, 19(1): 111-138.

[37] 彭宇，王建民，彭喜元. 基于回声状态网络的时间序列预测方法研究[J]. 电子学报, 2010, 38(z1):148-154.

PENG Y, WANG J M, PENG X Y. Researches on time series prediction with echo state networks[J]. Acta Electronic Sinica, 2010, 38(z1):148-154.

[38] GEEM Z W, KIM J H, LOGANATHAN G V. A new heuristic optimization algorithm: harmony search [J]．Simulations, 2001, 76(2): 60-68．

[39] 欧阳海滨，高立群，邹德旋, 等. 和声搜索算法探索能力研究及其修正[J]. 控制理论与应用，2014, 31(1)：57-65.

OUYANG H B, GAO L Q, ZOU D X, et al. Exploration ability study of harmony search algorithm and its modification[J]. Control Theory and Applications, 2014, 31(1)：57-65.

[40] MAHDAVI M, FESANGHARY M，DAMANGIR E. An improved harmony search algorithm for solving optimization problems[J]．Applied Mathematics and Computation, 2007, 188(2): 1567-1579．

[41] ALATAS B. Chaotic harmony search algorithms [J]. Applied Mathematics and Computation, 2010, 216(9): 2687-2699.

[42] DAS S, MUKHOPADHYAY A, ROY A, et al. Exploratory power of the harmony search algorithm: analysis and improvements for global numerical optimization [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2011, 41(1): 89-106.

[43] 彭宇，王建民，彭喜元.储备池计算概述[J]. 电子学报, 2011, 39(10):2387-2396.

PENG Y, WANG J M, PENG X Y. Survey on reservoir computing[J]. Acta Electronic Sinica, 2011, 39(10): 2387- 2396.

Network traffic multi-step prediction based on chaos theory and improved echo state network

TIAN Zhong-da, LI Shu-jiang, WANG Yan-hong, WANG Xiang-dong

(College of Information Science and Engineering, Shenyang University of Technology, Shenyang 110870, China)

Network traffic prediction was an important problem of network management and network congestion control. In order to solve this problem, a network traffic prediction method based on chaos theory and improved echo state network was proposed. Firstly, network traffic sample with different time scale were analyzed by 0-1 test algorithm for chaos and maximum Lyapunov exponent, the calculation results show that the network traffic has chaotic characteristics in different time scale. The phase space reconstruction technique was introduced for the prediction of network traffic, the delay time was determined through the C-C method, the embedding dimension was determined through the G-P algorithm. Network traffic time series was processed with phase space reconstruction, the multi-step prediction of network traffic was achieved by an improved echo state network. In order to improve the prediction precision, the key dynamic reservoir and prediction parameters of echo state network were optimized by an improved harmony search algorithm. Through the simulation on public and actual network traffic data, the results verify the proposed prediction method has higher prediction accuracy and smaller prediction error.

network traffic, chaos, echo state network, time scale, prediction

TP393

A

10.11959/j.issn.1000-436x.2016053

2015-03-31；

2015-12-02

国家自然科学重点基金资助项目（No.61034005）；辽宁省博士启动基金资助项目（No.20141070）

The National Natural Science Foundation of China (No.61034005), Liaoning Province Doctor Startup Fund (No.20141070)

田中大（1978-），男，辽宁沈阳人，博士，沈阳工业大学讲师，主要研究方向为时间序列建模与预测、网络控制系统时延补偿、非线性系统预测控制等。

李树江（1966-），男，辽宁沈阳人，博士，沈阳工业大学教授，主要研究方向为复杂工业过程建模与控制、智能控制技术的应用研究与开发等。

王艳红（1967-），女，辽宁沈阳人，博士，沈阳工业大学教授，主要研究方向为生产调度与优化、先进制造信息系统、分布式信息处理与智能控制。

王向东（1959-），男，辽宁沈阳人，博士，沈阳工业大学教授，主要研究方向为生产调度与优化、复杂工业过程建模与控制、智能控制技术的应用研究与开发。