波纹芯体夹层板分频段隔声性能多参数优化

李会荣，郑　辉，2，杨浩森，米永振

波纹芯体夹层板分频段隔声性能多参数优化

李会荣1，郑辉1，2，杨浩森1，米永振1

（1.上海交通大学 振动、冲击、噪声研究所，上海 200240；2.高新船舶与深海开发装备协同创新中心，上海 200240）

应用遗传算法与梯度算法相结合的混合优化算法，在结构质量及整体刚度约束下，分两个频段对波纹芯体夹层板在中置点声源激励下平均透射声功率进行单参数和多参数优化分析，其中优化目标函数，即夹层板透射声功率用谱元法和Rayleigh积分进行建模计算。优化结果表明，单参数和多参数优化都能明显改善波纹芯体夹层板在高频段（701 Hz～1 500 Hz）的隔声性能，但两种方法在低频段（1 Hz～700 Hz）效果均不显著，证明单纯针对结构参数优化能够有效地抑制由局部模态引起的透射声峰值，但是对结构整体模态引起的透射声峰值影响有限。进一步对比表明，对具有多个结构参数的波纹芯体夹层板，其隔声性能多参数联合优化结果明显优于单参数优化结果。

声学；夹层板；波纹芯体；声透射；参数优化；谱元法

波纹芯体夹层板是上下两层金属板之间由波纹状芯体板连接而成，因其具有刚度-质量比（比刚度）和强度-质量比（比强度）大的优点，被广泛应用于对轻量化要求较高的高速载运工具。通常来说，高速运载工具在行驶时随着运载工具运行速度的提高，往往舱室噪声会急剧增大。为保证乘客拥有良好的乘坐舒适性，要求作为壁板的波纹芯体夹层板具有良好的隔声性能。关于夹层板隔声性能的研究很多。在理论研究方面，Lee和Kim采用针对周期性夹层板的空间谐波建模方法，在将筋板简化为刚体的基础上研究了加筋板的声透射问题［1］。Xin等在研究三明治夹层板中的声透射问题采用波传导模型，考虑了筋板剪切、弯曲和扭转运动，理论模型相对完整［2］。孙加平等采用传递矩阵法研究了三明治板的材料和结构参数对高速列车底板隔声性能的影响［3］。除了理论研究外，数值计算方法在对夹层板的振动-声学问题的研究中也被广泛应用。黄勇和马克俭根据空腹夹层板的构造特点，提出了基于板-块体元模型的空腹夹层板有限元分析方法［4］。陈波等也使用有限元方法研究了工程中常见的夹层板结构动力学响应［5］。毕波等在考虑夹层板的剪切变形的同时计入了芯板的横向变形，建立了等效单层模型的有限元动力学方程［6］。

夹层板结构的隔声性能与结构的材料参数和几何参数密切相关，因此很多学者致力于研究夹层板结构参数对其振动声学性能的影响，特别是针对夹层板结构参数的优化。Anthony等使用遗传算法对一个二维加筋悬臂梁进行了尺寸优化，使传递到最外端梁的振动能量最小［7］。Wang用高阶夹层梁理论研究了在满足机械刚度与隔声性能前提下结构的轻量化问题［8］。李智等用有限元法对复合层板建立了数值模型，分析了板的结构的材料和几何参数对减振降噪的作用［9］。这些研究中基本都采用了有限元计算方法。然而，有限元方法建模过程复杂，变参数计算中结构参数每次变化都需要重复建模。同时，为保证较好的高频计算精度，要求单元尺寸足够小，导致高频域隔声性能优化时间过长。

相对而言，谱元法（spectral element method，SEM）则为需要多次循环计算的优化问题提供了一种更好的选择。该方法于1984年被提出，最初用于流体力学计算［10］。之后学者们又将谱元法应用到结构振动方面的研究。Chakraborty和Gopalakrishnan用谱元法研究了夹层板中的波传播问题［11］。Lee U采用谱元法研究了两梁之间接头的动力学特性，且计算结果与实验符合得较好［12］。吴志静等建立了谱单元动力学刚度矩阵，对钢架结构的动力学响应进行了分析，证明了谱元法相较于传统有限元法具有计算精度高的优点，特别是高频计算精度高［13］。Wu等研究了周期性板结构的振动响应，证明了谱元法应用于周期性结构振动建模计算的高效性［14］。谱元法的这些优势使其非常适合用于求解波纹芯体夹层板这类周期结构隔声优化问题时所需的循环计算。

本文以波纹芯体夹层板为研究对象，采用遗传算法和梯度算法组合构成的优化算法对中置点声源激励下构件的频段平均透射声功率分别进行了单参数和多参数优化。优化以结构质量及整体刚度为约束条件、分低频和高频两个频段进行，目标为频段平均透射声功率最小。其中优化频段的选取基于波纹芯体夹层板参考模型的振动模态分布，低频段中所有结构模态均为整体模态，高频段则包含部分局部模态；而优化目标函数，即结构在声激励下的辐射声功率，先运用谱元法计算得到结构振动响应、然后通过Rayleigh积分计算得到。最后对两个不同频段的多参数和单参数优化结果进行对比分析讨论。

2　透射声功率计算模型

2.1结构及声透射计算理论模型

典型波纹芯体夹层板由上板、波纹芯体板和下板组成，其三维结构如图1所示。

图1　波纹芯体夹层板三维结构

图2给出夹层板的二维截面图。夹层板总长为L，空腔高度（上下面板间距）为H，上下面面板厚度分别为h1、h3，中间波纹芯体板厚为h2，筋板倾角为α。

因为夹层板平面内沿波纹垂直方向的横向弯曲刚度远大于波纹方向，通常假设夹层板沿波纹垂直方向无限延伸，使得三维夹层板的隔声问题简化为图2所示的二维结构（夹层梁）的隔声问题，其声透射计算模型如图3所示。

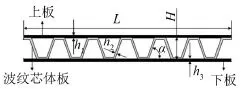
图2　波纹芯体夹层板二维尺寸图

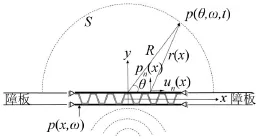
图3　波纹芯体夹层梁声透射示意图

在图3所示的声透射计算模型中，波纹芯体夹层梁两端简支并置于半无限长声障板之中，下简支梁受到点声源的激励而振动，其振动能量通过芯梁结构及梁内声腔传至上梁，引起上梁振动并向外辐射声波。考虑到波纹芯体夹层梁刚度较空气刚度大很多，可将空腔的声传递路径忽略［15］，仅考虑结构路径传声。

2.2结构振动响应的谱元法计算

基于图3所示声透射模型，采用谱元法（Spectral element method，SEM）计算结构在声激励下的振动响应。谱元法结合了传统有限元方法和谱方法的优点，与传统有限元方法的区别在于此方法基于动态刚度矩阵求解［16］。李兰清等关于加筋双层板声透射的研究中通过有限元方法验证了谱元法计算夹层板结构的精度［17］，该文中给出了谱元法计算夹层板在入射简谐声波激励下振动响应的详细数学推导，此处不再赘述。图4给出了谱元法及传统有限元计算波纹芯体夹层梁在下梁受到1 Hz～2 000 Hz平面波声激励作用下上梁振动能量的结果比较。

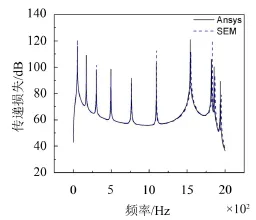
图4　上梁振动能量谱元法计算结果与有限元对比

从图4可以看出，谱元法和有限元法得到的振动能量-频率曲线在整个计算频段内吻合很好。更重要的是，谱元法计算耗时不超过有限元法计算时间的5%。这对于下文将要讨论的波纹芯体结构的隔声优化具有重要意义。

2.3声辐射计算

应用谱元法计算得到结构的振动响应后，结合Rayleigh积分可以计算结构向外的辐射声场［18］。根据Rayleigh积分，图3中半径为R的半圆面上任意一点由结构上梁振动所引起的声压为

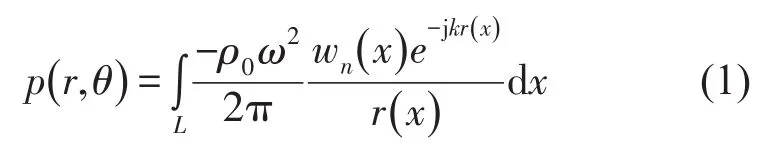
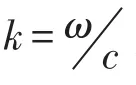
在整个半圆面S上对声强积分即可得到波纹芯体夹层梁通过上梁向外辐射的声功率，即结构的透射声功率［19］

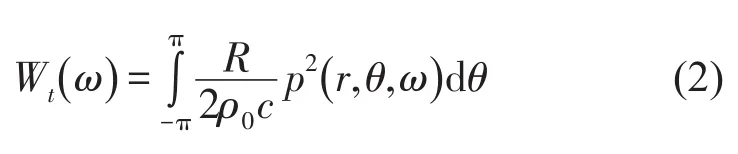
3　隔声性能的优化分析

在进行波纹芯体夹层梁的隔声性能优化之前，需要首先确定参考模型，并根据参考模型的频响特性选择优化目标频段以及优化约束条件。

3.1优化频段选择

参考模型截面如图2所示，芯体为6周期波纹梁（12筋梁），上、下梁及芯体的材料都相同，结构的材料参数和几何参数如表1所列。对参考模型进行模态分析，得出参考模型横向振动模态在1 Hz～700 Hz频段全部为整体弯曲模态，频率超过700 Hz后局部模态才开始出现，701 Hz～1 500 Hz频段内整体模态占比约为50%。因此，为了研究结构模态对隔声性能优化的影响，将优化的目标频段分为1 Hz～700 Hz（低频段）和701 Hz～1 500 Hz（高频段）。

表1　参考模型的材料及几何参数

3.2优化问题的数学表述

3.2.1单参数优化问题表述

相对于隔声领域广泛研究的单层板和双层板结构，波纹芯体夹层梁影响隔声性能优化目标函数的结构参数较多，若进行多参数优化，容易产生计算量大、优化效率低的问题，对于需要考虑时间成本的情况，单参数优化是较好的选择，因此首先进行单参数优化。

以入射声波频段内平均透射声功率来评价构件在该频段的隔声性能，将目标频段内的平均透射声功率最小化作为优化目标，分别进行两个目标频段的优化：低频段（1 Hz～700 Hz）和高频段（701 Hz～1 500 Hz）。目标函数计算式为

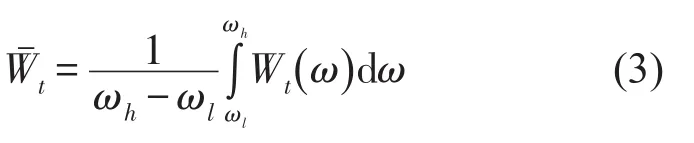
其中ωh、ωl分别为频段的圆周频率上下限。

考虑到对结构有轻量化要求，限定其总质量不得超过参考模型的质量，即其截面面积不得超过参考模型的截面面积。另外，为了保证夹层梁具有一定的整体刚度，其1阶固有频率不可过低［20］，因此要求第1阶固有频率不得低于参考模型的1阶固有频率值。

波纹芯体夹层梁结构参数中影响透射声功率的主要参数有上下梁厚度h1、h3，芯体厚度h2以及芯体倾角α［21］。在单参数优化中，仅保留一个设计参数作为优化变量，并通过附加面积不变约束条件建立与其他设计变量的关系，从而将其引入优化问题中。据此，设计了两个单参数优化组，优化组一（Optimization I）和优化组二（Optimization II），其中优化组一考察了上梁厚度的优化效果，而优化组二是考察了芯体倾角的优化效果。单参数优化两个优化组的优化变量取值范围以及约束条件如表2所列。

表2　单参数优化变量及约束

3.2.2多参数优化问题表述

考虑到若同时优化对目标函数有影响的四个主要的结构参数，则有可能得到更好的优化效果，进一步进行多参数的联合优化。多参数联合优化的目标函数和单参数优化相同。优化变量及其取值范围为

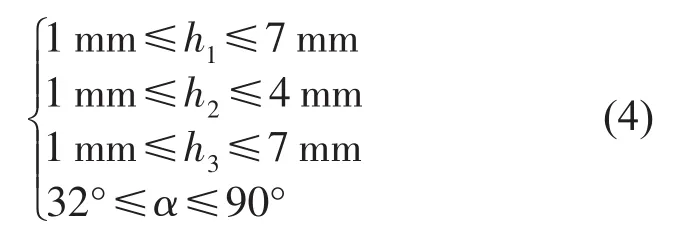
约束条件为截面积约束和1阶固有频率约束

其中S为夹层梁截面积，S0为参考模型夹层梁截面积；f为11阶固有频率，f0为参考模型的1阶固有频率。

3.3优化方法

对上述优化问题使用遗传算法和梯度算法的组合优化算法进行优化计算。遗传算法因计算的随机性使其具有良好的全局搜索能力，然而后期计算效率低。而梯度算法则能快速地找到局部最优解。因此利用遗传算法的全局探索能力找到全局优化解，然后将此全局优化解作为梯度优化算法的初始值，在其周围进行局部搜索，寻找更加精确的最优解。

为了保证优化解的可靠性，遗传算法每次优化至少60代，每代个体数为500，当连续4代最优结果相对误差小于0.1%时，即认为优化收敛。

3.4优化结果及讨论

3.4.1单参数优化

低频段为1 Hz～700 Hz，在此频段内分别根据优化组一和优化组二对夹层梁的透射声功率进行优化，优化结果以及优化模型与参考模型性能指标参数对比如表3所示。这里仅给出了优化变量的优化结果，其余设计变量可通过约束条件求出，或与参考模型保持一致。

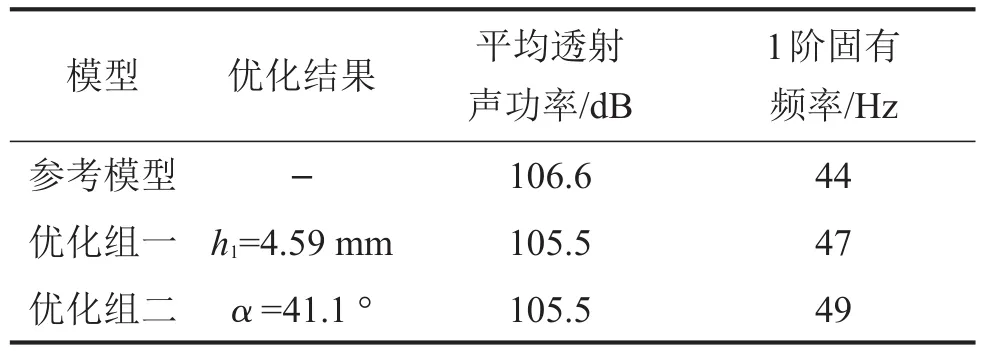
表3　低频段单参数优化结果

由表3可知，两个优化组透射声功率相对于参考模型均降低了1.1 dB，降幅较小。将优化模型与参考模型在优化频段内的透射声功率谱进行对比，图5给出了两组优化结果与参考模型的透射声功率频谱曲线对比。从图中可以看出，两个单参数优化组在低频段内对透射声功率优化效果表现在各峰值有所降低，然而峰值个数并没有减少，优化效果不明显。

高频段为701 Hz～1 500 Hz，同样分别对两个优化组进行单参数优化，优化结果如表4所列。优化前后的频谱特性曲线如图6所示。

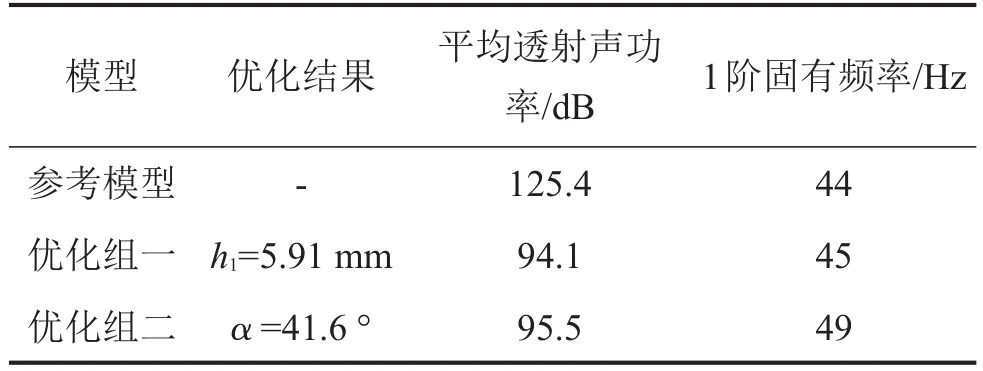
表4　高频段单参数优化结果

由表4可以看出在高频段下，相对于参考模型，两个优化组的优化模型平均透射声功率大幅降低，其中优化组一降低了31.3 dB；优化组二降低了29.9 dB。

从图6可以看出，高频段下两组单参数优化相对于参考模型均得到了较好的优化效果：频段内平均透射声功率大幅降低；频段内峰值个数也有减少。

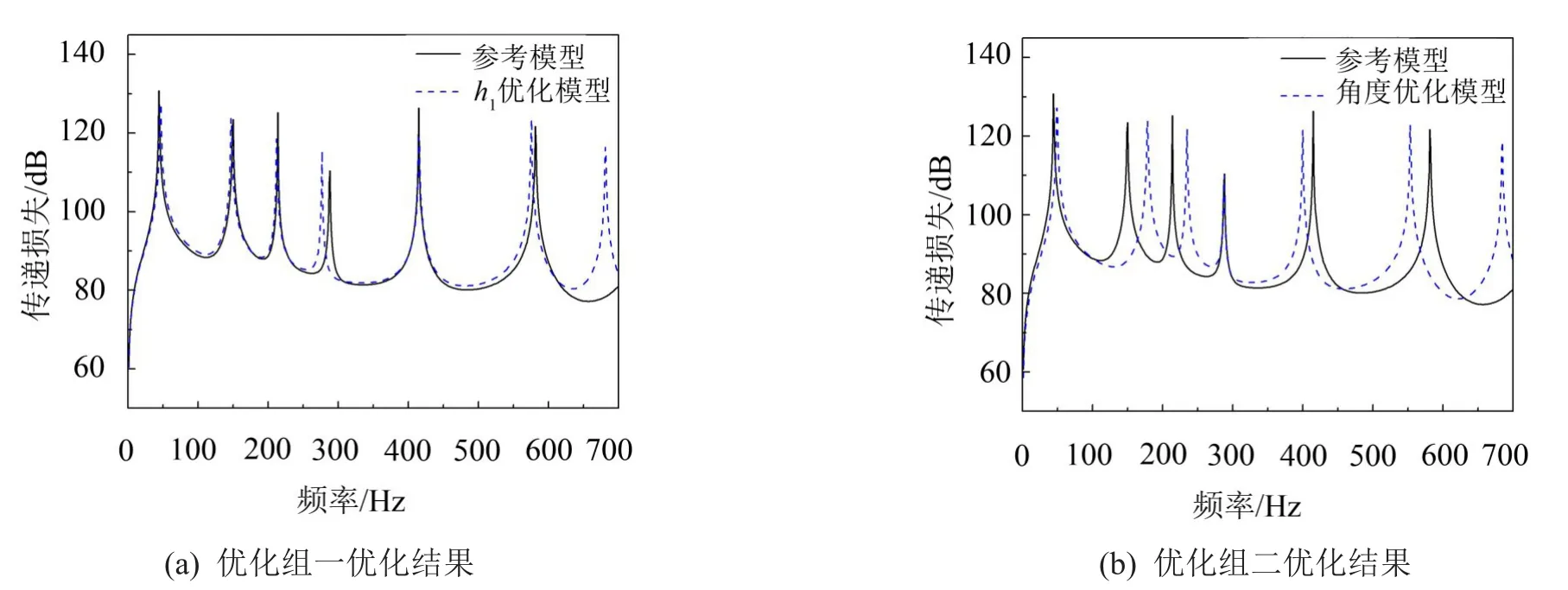
图5　低频段下两组单参数优化结果

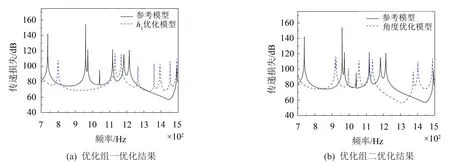
图6　高频段下两组单参数优化结果

3.4.2多参数优化

多参数优化仍然分别在低频段（1 Hz～700 Hz）和高频段（701 Hz～1500 Hz）进行，优化后模型的结构参数如表5所示。表6给出了优化后模型的1阶固有频率、对应频段的平均透射声功率及截面相对面积（相对于参考模型）。

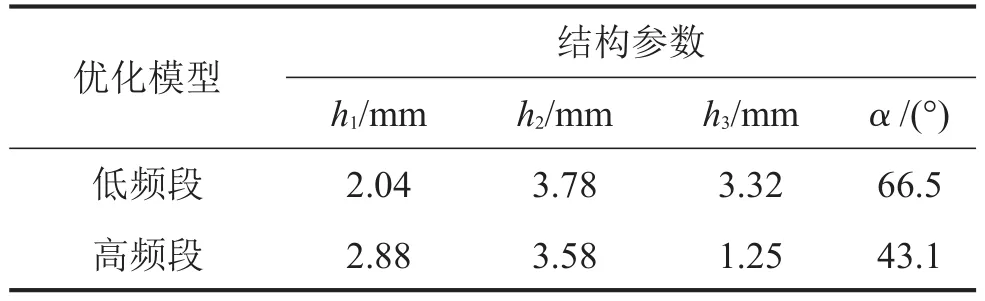
表5　优化后模型的结构参数

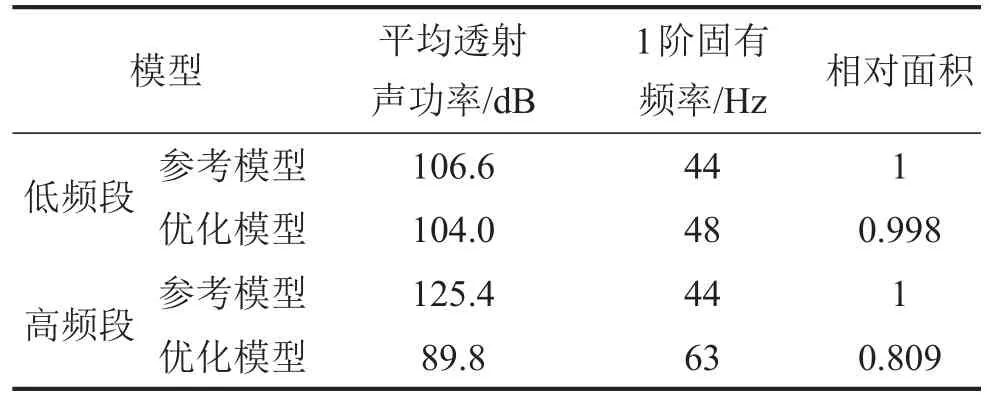
表6　优化后模型的性能指标

图7和图8分别给出了两个频段优化前后模型的透射声功率曲线。从图7所示的透射声功率频谱曲线比较可以看出，对于低频段，优化后的结构相对于参考模型峰值个数并没有减少，只是使一些峰值有所降低。图8中结果表明，在高频段，优化后的结构隔声性能明显优于参考模型，优化后模型不仅拥有更低的透射声功率峰值，而且透射峰数量相对于参考模型也大量减少。

经过多参数联合优化，相对参考模型，低频段平均透射声功率降低了2.6 dB，高频段平均透射声功率降低了35.6 dB。

3.4.3单参数优化与多参数优化结果比较

表7列出了分别使用单/多参数优化得到的优化结果。可以看出，对低频段而言，不管采用单参数优化还是多参数优化方法，透射声功率降低效果都不明显；反之，对高频段，两种优化方法都得到了很好的优化效果。

由优化目标频段选取可知，参考模型在低频段内结构的模态全部为整体模态，而高频段中约50%为局部模态。本文对波纹芯体夹层梁结构的优化是几何尺寸的优化，而不改变模型的拓扑构型。单纯进行尺寸优化对结构的整体模态影响有限，因而对低频段的优化效果不佳；几何尺寸优化会改变局部模态从而使因局部模态引起的共振峰值有效降低，故对于有较多局部模态的高频段优化效果显著。

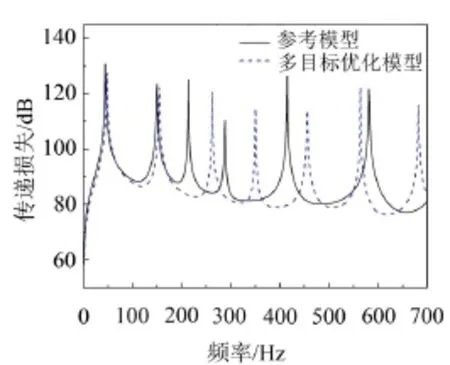
图7　低频段透射声功率优化结果

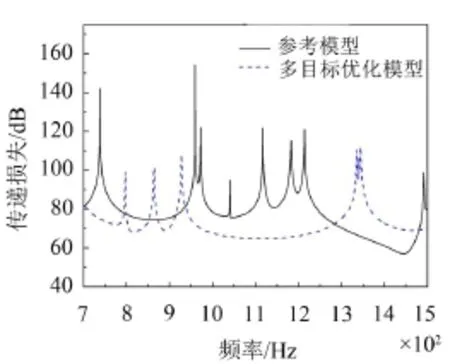
图8　高频段透射声功率优化结果

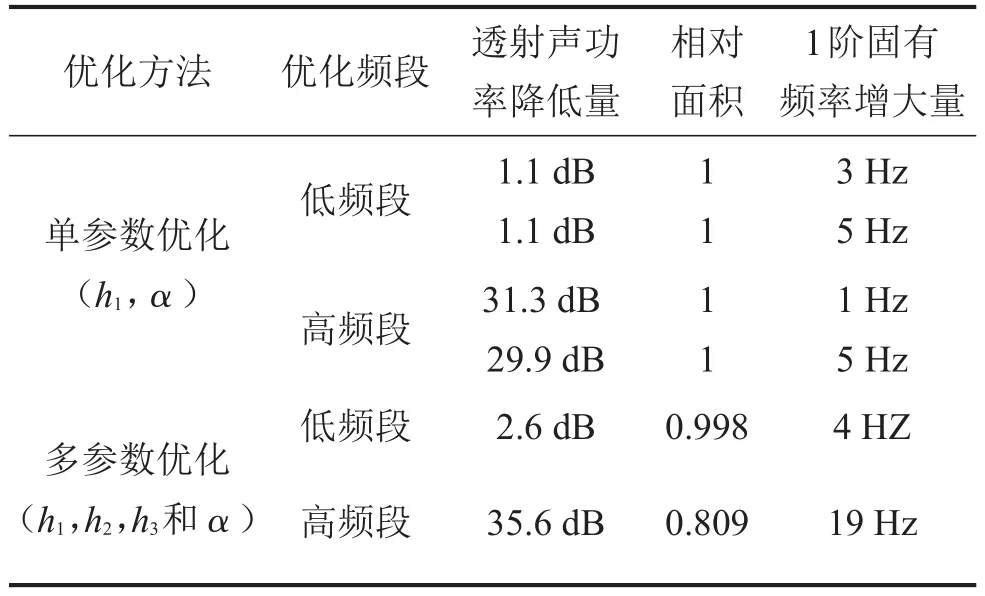
表7　单参数与多参数优化结果比较

为进一步证明这一结论，本文选取了更高的频率段，即1 000 Hz～2 000 Hz，对参考模型在此进行了多参数优化。参考模型的模态分析结果显示，此频段内局部模态占比为约70%。优化结果如图9所示。从图中可以看出，优化模型在优化频段内相对于参考模型透射声功率大幅度降低，透射声功率峰值数量减少很多。

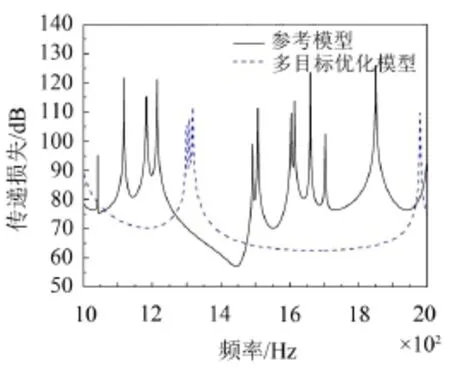
图9　1 000 Hz～2 000 Hz优化结果

将单参数优化与多参数优化进行同频段优化结果对比，发现多参数优化不但使透射声功率降低更多，并且使结构刚度增大、结构变轻。因此多参数优化效果明显优于单参数优化。

4　结语

本文针对波纹芯体夹层梁的隔声性能分别进行了单参数和多参数优化。优化结果表明，针对高频段（700 Hz～1 500 Hz）的隔声性能优化结果明显优于低频段（1 Hz～700 Hz），这是由于随着频率的增加，结构局部模态增多，改变夹层梁芯体结构参数能够有效地改变局部模态，但是对整个结构的整体模态影响有限。

通过对比多参数优化与单参数优化的结果说明，对于结构参数较多的复杂构型，多参数优化能够更大限度地提高整体结构的隔声性能。虽然如此，考虑到结构在低频段隔声性能通过单纯结构参数优化难以得到很好的效果，若要进一步提高结构的隔声性能，应从其他途径考虑，如阻尼处理、主动控制等。

［1］LEE J H，KIM J.Analysis of sound transmission through periodically stiffened panels by space-harmonic expansion method［J］.Journal of Sound and Vibration，2002，251（2）：349-366.

［2］XIN F X，LU T J.Analytical modeling of wave propagationinorthogonallyrib-stiffenedsandwich structures：Sound radiation［J］.Computers&Structures，2011，89（5）：507-516.

［3］孙加平，张丽荣，孙海荣，等.高速列车夹芯地板结构隔声特性研究［J］.噪声与振动控制，2014，34（4）：39-43.

［4］黄 勇，马克俭.基于板-块体模型的空腹夹层板有限元分析［J］.贵州工业大学学报（自然科学版），2002（31）：10-14.

［5］陈波，黄勇，马克俭.空腹夹层板有限元分析的两种模型［J］.建筑结构，2001：58-60.

［6］毕波，徐干成.一种夹层板结构的动力有限元方法［J］.空军工程大学学报（自然科学版），2002，3（3）：77-80.

［7］ANTHONY D K，ELLIOTT S J，KEANE A J.Robustness ofoptimaldesignsolutionstoreducevibrationtransmission in a lightweight 2-D structure，part I：Geometric design［J］.Journal of Sound and Vibration，2000，229（3）：505-528.

［8］WANG T，LI S，NUTT S R.Optimal design of acoustical sandwich panels with a genetic algorithm［J］.Applied Acoustics，2009，70（3）：416-425.

［9］李智，殷祥超，何兴华，等.复合层板减振降噪特性的数值模拟研究［J］.噪声与振动控制，2006，26（6）：27-30.

［10］PATERA A T.A spectral element method for fluid dynamics：laminar flow in a channel expansion［J］. Journal of Computational Physics，1984，54（3）：468-488.

［11］CHAKRABORTY A，GOPALAKRISHNAN S.A spectral finite element model for wave propagation analysis in laminated composite plate［J］.Journal of Vibration and Acoustics，2006，128（4）：477-488.

［12］LEE U.Dynamic characterization of the joints in a beam structure by using spectral element method［J］.Shock and Vibration，2001，8（6）：357-366.

［13］吴志静，李凤明，胡恒山，等.谱元法在求解刚架结构动力学问题中的应用［J］.动力学与控制学报，2012，10（1）：71-75.

［14］WU Z J，LI F M，WANG Y Z.Study on vibration characteristics in periodic plate structures using the spectral element method［J］.Acta Mechanica，2013，224（5）：1089-1101.

［15］CHENG L，LI Y Y，GAO J X.Energy transmission in a mechanically-linked double-wall structure coupled to an acoustic enclosure［J］.The Journal of the Acoustical Society ofAmerica，2005，117（5）：2742-2751.

［16］LEE U.Spectral element method in structural dynamics ［M］.John Wiley&Sons，2009.

［17］李兰清，郑辉.基于谱元法的加筋双层板声透射分析［J］.噪声与振动控制，2015，35（3）：181-185.

［18］FAHY F J，GARDONIO P.Sound and structural vibration：radiation，transmissionandresponse［M］. Academic press，2007.

［19］杜功焕，朱哲民.声学基础［M］.南京：南京大学出版社，2001.

［20］BERRY A，NICOLASJ.Structuralacousticsand vibrationbehaviorofcomplexpanels［J］.Applied Acoustics，1994，43（3）：185-215.

［21］SHEN C，XIN F X，LU T J.Theoretical model for sound transmission through finite sandwich structures with corrugatedcore［J］.InternationalJournalofNon-Linear Mechanics，2012，47（10）：1066-1072.

Multi-parameter Optimization of the Sound Insulation Performance of a Corrugated Core Sandwich Plate in Two Different Frequency Ranges

LI Hui-rong1，ZHENGHui1，2，YANG Hao-sen1，MI Yong-zhen1
（1.Institute of Vibration，Shock and Noise，Shanghai Jiaotong University，Shanghai 200240，China；2.Collaborative Innovation Center forAdvanced Ship and Deep-sea Exploration（CISSE），Shanghai 200240，China）

A hybrid optimization combining genetic algorithm with gradient-based algorithm is applied to minimize the average radiation sound power of a corrugated-core sandwich plate under point sound source excitation in two specific frequency bands with its structural mass and stiffness constrained.With the sound transmission power of the sandwich plate as the target function of optimization，the spectral element method and Rayleigh's integral are applied to the model establishment and analysis.The results show that the optimization results of both single-variable and multi-variable optimizations can significantly improve the isolation performance of the corrugated core sandwich plate in the high frequency band（701 Hz-1500 Hz）.But both optimization methods are less effective in low frequency band（1 Hz-700 Hz）.It implies that the corrugated core parameters optimization can effectively suppress the sound radiation peaks caused by local modes，but has very little suppression effect on the peaks caused by global modes.Further comparison of the results obtained through single-variable optimization and multi-variable optimization shows that for the structure of corrugated core sandwich plate with multiple parameters，the multi-variable optimization is much better than the single-variable optimization in soundinsulating performance.

acoustics；sandwich plate；corrugated core；sound transmission；parameter optimization；spectral element method

O327 O42

ADOI编码：10.3969/j.issn.1006-1335.2016.03.039

1006-1355（2016）03-0190-07

2015-11-16

国家自然科学基金资助项目（51275285）

李会荣（1990-），女，湖北省汉川市人，硕士研究生，主要研究方向为噪声与振动控制。

郑辉，男，教授，博士生导师。E-mail：huizheng@sjtu.edu.cn