基于耦合Duffing振子的微弱故障信号检测
2016-10-14王晓东赵志宏杨绍普
王晓东,赵志宏,杨绍普
基于耦合Duffing振子的微弱故障信号检测
王晓东1,2,赵志宏2,杨绍普1,2
(1.石家庄铁道大学 机械工程学院,石家庄 050043;2.河北省交通安全与控制重点实验室,石家庄 050043)
针对传统信号处理方法在低信噪比条件下对微弱信号检测的不足,提出一种对双Duffing振子进行阻尼项耦合的方法,通过对此系统进行动力学分析,比单个Duffing振子具有更加复杂的动力学行为。阐述了基于相平面变化的微弱信号检测原理,对时间进行尺度的变换,实现了未知频率信号的检测,最后对微弱脉冲信号进行检测以及真实的故障轴承的早期诊断,取得了较好的效果,该方法在无线通信、雷达系统、旋转机械早期故障诊断等领域具有广阔的前景。
振动与波;双耦合Duffing振子;混沌;周期信号;故障诊断
自1990年Pecora and Carrel提出混沌同步概念以来,混沌同步理论和应用研究得到了迅速的发展[1]。相继提出了完全同步、广义同步、滞后同步、哈密顿系统的测度同步等同步概念。同步是耦合非线性系统的合作行为最基本的表现之一,同步是物理学、电子技术、生物学、化学、光学等学科在非线性问题研究中的一个非常重要的课题[2-4]。人们在寻找新的同步方式的同时,也尝试着从更高的高度来研究这些同步形式。例如,从研究低维混沌发展到研究高维时空混沌就是一种新的尝试。双耦合Duffing混沌振子系统就是高维时空混沌系统。耦合振子系统的动力学行为远比单振子系统复杂,它的同步和控制过程为在不同领域中的应用提供可能,同时也引起了世界各国学者的广泛关注[5-8]。
本文研究的是双耦合Duffing混沌振子在微弱信号检测中的应用。利用双耦合Duffing振子混沌系统对微小信号敏感性和对强噪声的免疫力[9-11],以及两个Duffing振子互相联系互相控制的工作过程,提高系统在临界分岔处的稳定性,为混沌振子系统检测微弱信号提供新的途径。通过对双耦合Duffing振子系统模型建立、动力学分析及应用于微弱信号检测的研究表明它在正弦信号、脉冲信号检测方面具有很好的应用前景,最后通过对真实故障轴承信号分析,获得较好的效果,为工程实际中旋转机械早期故障诊断应用提供了一种可借鉴的方法[12-13]。
1 双耦合Duffing振子模型的建立
根据文献中出现过的对位移项进行耦合[14]的方式,本文对双耦合Duffing振子采用以下特定的耦合方式,即对阻尼项进行耦合,建立数学模型如下
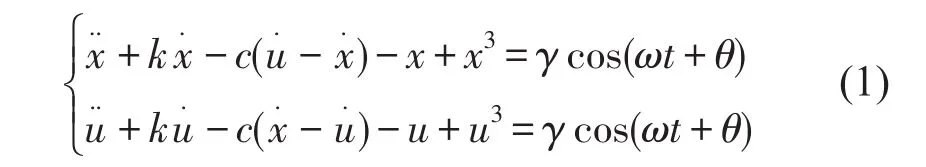
上式中k表示阻尼系数,一般取k=0.5,c表示耦合系数,γcos(ωt+θ)表示周期策动力。
1.1耦合系数与动力学行为的关系
c表示耦合系数,c的取值越大说明耦合的强度越高,不同振子间的同步性越强,若c=0,则两振子之间的耦合作用消失,此时系统的动力学行为与单个Duffing振子系统相同。当c≠0时,系统的变量会在耦合作用的影响下随时间趋于同步。由图1可以看出两个系统在t=12 s后很快达到了同步行为,而且通过对阻尼耦合系数c取不同的数值进行大量实验验证表明对于阻尼耦合的情况与位移耦合情况正好相反,阻尼耦合系数越大,相同步的时间越长,这是合理的。

图1 双耦合系统变量(x-u)时间历程图
1.2双耦合Duffing振子的分岔图
分岔是指非线性系统定性行为随着参数变化而发生质变的现象,分岔研究不仅能揭示系统不同状态之间的联系和转化,而且是研究失稳和混沌产生机理和条件的重要途径,所以分岔与系统的结构稳定性有着十分密切的联系。图2是此双耦合Duffing混沌振子系统在特定参数(k=0.5,c=2,ω=1.0rad/s)下的分岔图,通过此图可以看出随着策动力γ的不断增大,系统出现混沌与周期的交替现象,当γ比较小时,系统表现为周期一运动;继续增大γ,在γ=0.35附近时,系统出现倍周期分岔,表现为周期二运动;再继续增大γ,系统出现混沌状态,最终在γ=0.82附近,由混沌状态又进入稳定的周期一状态。

图2 双耦合系统的分岔图
1.3双耦合Duffing振子系统的检测原理
通过上述方程式(1)的耦合模型,建立Simulink仿真模型,采用定步长4阶Runge-Kutta方法进行研究,取步长h=0.01 s,耦合系数c=2,选择其它参数不变时,改变策动力幅值γ,当γ较小时,相轨迹表现为Poincare映射意义下的吸引子,相点围绕焦点做周期振荡,逐渐增加γ达到临界值γ=0.826时,系统经历同宿轨道,倍周期分岔直至混沌运动(如图3(a)所示),系统在混沌状态的时间相对较长,而且相轨迹局限在某一个范围内,继续增大策动力γ,系统进入到临界大尺度周期状态。此时γ略微增加超过阈值γd,系统将以外加周期力的频率进行大尺度的周期振荡(如图3(b)所示),此后相轨迹不在杂乱无章,而是沿着固定的轨道重复下去。
2 双耦合Duffing振子对微弱正弦信号的检测
根据双耦合Duffing振子的动力学行为特点,建立微弱信号检测的数学模型如下所示。

其中γcos(ωt+θ)为内置信号,acos(ωt+φ)为待测的信号,n(t)高斯白噪声。对上述构造的系统进行仿真实验时,此系统检测原理与单Duffing振子一样(即选择从临界周期到周期的轨迹相变为判断系统输入是否带有周期信号的依据),当双耦合Duffing振子系统调整到从混沌状态到大周期的临界状态时,亦即γ将设置在临界分岔状态附近。然后加入待测的微弱周期信号,当待测信号加入系统中经过暂态过程以后,系统稳定在某一运动形式上,计算机通过辨识系统容易得知系统是处于混沌还是大尺度周期运动状态。由此,可判断输入信号是纯噪声还是混有微弱周期信号。
当输入待测信号后,整个驱动力变为

图3 双耦合Duffing振子系统相图

由上述双耦合Duffing振子非线性系统相态变化的仿真结果显示,可求得此时信号的信噪比检测门限为

对于传统方法,很难检测到信噪比-10 dB的信号,这也是一些传统方法的局限所在,同时验证了混沌检测系统的优势,能够实现低信噪比下的微弱周期信号检测。因此混沌系统具有很好的发展前景和研究价值。
当相位θ=0时

其中

从上式可以看出系统相态和相位之间的关系。调整策动力可以使待测信号的相位满足下式:π-arccos[(a/2γ)]≤φ≤π+arccos[(a/2γ)]使系统出现混沌状态,不产生大周期变化。
当系统没有同频率待测周期的信号输入时,系统输出呈现如图4(a)杂乱无章的混沌现象。当系统有相同频率的待测周期信号acos(ωt),其中a=0.003,输入系统时,系统输出呈现如图4(b)的大周期现象(前期有个不稳定的过渡状态,随后进入稳定的大周期)。

图4 双耦合Duffing振子的系统相图
2.1对未知频率信号的检测
上面只是研究了周期频率ω=1rad/s的情况,对于实际工程信号而言,要想将某一频率成分的信号检测出来,就要将方程(1)的驱动信号频率设置为该待测信号的频率值。然而这个待测信号的频率往往是很难确定的。为了减少计算的麻烦,可以对方程进行时间尺度的变换,改变信号的时间尺度,在不改变其离散数值的情况下,将其在时间尺度上进行压缩或放大,这种时间尺度并不改变参与计算数据,只是在时间轴上对数值进行了重新排序。
令t=ωτ,则有:x(t)=x(ωτ);

代入方程(1)整理得

这样只需调整方程式(4)中的ω值,来适应外界不同频率的周期信号,从而实现对外界不同频率微弱信号的检测。由于状态方程(4)是由上述方程派生出来的,只是从另一时间尺度观察耦合非线性系统的动态,因此前面所讨论的结果都是适用的。对于上述变形耦合非线性系统的模型,设置其它参数不变,进行不同频率的周期信号检测。在耦合方程改进后,可根据实际情况调整参数以进行系统各个状态的仿真和计算。
3 微弱脉冲信号的检测
脉冲信号是一种离散信号,形式多种多样,波形在时间轴上不连续,但具有一定的周期性,因此也就为检测脉冲信号提供了可能。最常见的脉冲信号就是矩形波(方波),脉冲信号可以用来表示的信号有:脉冲编码调制、脉冲宽度调制、各种数字电路、高性能的时钟信号,因此对于微弱脉冲信号的检测是值得研究且有一定的应用价值。
下面是基于Simulink中脉冲发生器模块产生的一组信号(如图5所示),然后把该信号和噪声(此信号的信噪比为-14.8 dB)一起加入到双耦合Duffing振子检测系统中进行模拟实验,检测原理方法与微弱正弦信号是一样的,通过大量实验仿真表明此微弱脉冲信号检测的内驱动力依然可以是正弦信号(与脉冲信号同频率),不再需要改变内驱动力的波形,调节好此系统的临界阈值,进行仿真实验,观察系统相图的变化。

图5 脉冲信号
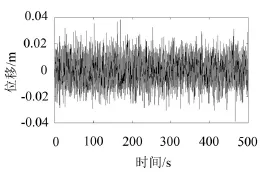
图6 加入噪声的脉冲信号
通过系统相图的变化(如图7所示,从混沌状态转变为大周期状态),可以看出此双耦合Duffing振子系统能有效地检测出混在噪声中的微弱脉冲信号,为以后数字电路、雷达通讯等故障信号检测提供了一种可能。
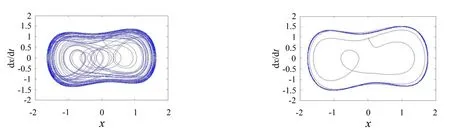
图7 双耦合Duffing振子系统相图
4 轴承的早期故障诊断
轴承故障是旋转机械中最为常见的故障,作为机械设备关键部件之一,早期故障发现显得尤为重要,如何在故障早期发展阶段及时发现故障,避免更大的损失,是故障诊断工作者一直研究的课题。
上面通过数值模拟实验实现了强噪声背景下的微弱周期信号的检测,为了能够在工程实际中得到验证,本文采用美国凯斯西储大学电气工程与计算机科学系轴承中心在网络上提供的实验数据[15]进行分析,试验台由功率为1.47 kW的电动机、扭矩传感器、测力计和电气控制装置组成。实验使用的轴承型号是SKF6205-2RS深沟球轴承,其结构参数见下表1。的特征频率的方法。

表1 轴承的结构参数
通过对此轴承用电火花加工的单点损伤,加工的故障直径为0.007英寸,采用16通道振动加速度传感器进行信号采集,将振动信号导入Matlab中,下图8分别是轴承内、外圈的故障时域图,很难观测出其故障特征频率。电机主轴转速为1 797 r/min,采样频率为12 000 Hz,由轴承的特性,专家们已经根据经验、理论总结推导出了计算滚动轴承各个部位
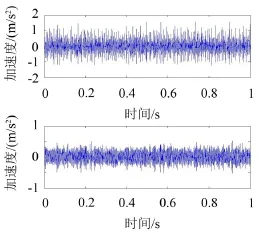
图8 轴承内、外圈的故障时域图
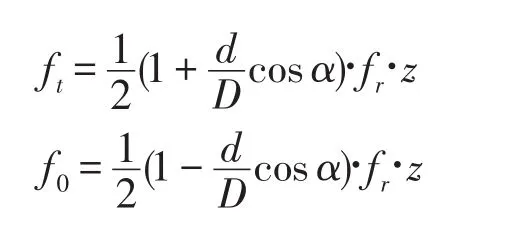
ft,f0分别表示内圈、外圈故障频率,其它参数含义已给出。根据表格中的各个参数可以计算出轴承内外圈的故障频率分别为:156.2 Hz和110.3 Hz。
通过以上实验数据分析,当系统输入正常信号时,系统状态没有发生变化,而输入内、外圈故障信号时,系统相图由混沌状态变为周期状态。由此可以说明系统相轨迹图发生了变化,并不是因为信号中其它因素引起的,而是由于采集的信号中存在与系统内置频率同频率故障信号的原因引起了系统相轨迹图的变化,由此判断出采集的信号是有故障的,并取得了较好的效果。

图9 双耦合Duffing振子系统相图
5 结语
本文针对传统的微弱信号检测问题,提出一种基于双耦合Duffing振子系统的检测方法,并对时间尺度进行变换,实现了任意未知频率周期信号的检测。而且通过对微弱正弦信号、脉冲信号的检测以及对实测故障轴承信号的早期诊断,取得较好的效果。为数字电路、雷达通讯等信号的检测提供了一种可鉴的方法,也为工程实际中旋转机械的早期故障诊断提供了有效的依据。
[1]吴勇峰,张世平,张金玮,等.环形耦合Duffing振子间的同步突变[J].物理学报,2011,60(2):202511-1-020511-6.
[2]吴勇峰,黄绍平,金国斌.基于耦合Duffing振子局部放电信号检测方法研究[J].物理学报,2013,62(13):1-7.
[3]杨东升,李乐,杨珺,等.基于双耦合混沌振子的未知频率信号检测[J].东北大学学报,2012,33(9):1226-1231.
[4]NIE CHUN-GAN,WANG ZHU-WEN.Application of chaosinweaksignaldetection[C]//IEEEof InstrumentationandMeasurementSociety,Shanghai University of Engineering Science,2011:528-531.
[5]卢莉萍,李翰山.强噪声下微弱信号检测方法的研究[J].陕西科技大学学报,2011,29(3):66-69.
[6]WANG J X,HOU C L.A method of weak detection based on duffing oscillator[C].2010 e-Education,e-Business,e-Management,and e-Learning,IEEE Conference,2010. 387-390.
[7]LI YUE,YANG BAO JUN,SHI YAO WU,et al.Chaosbased weak sinusoidal signal detection approach under colored noise background[J].Physica,2003,52(3):526-530.
[8]MAL X.Weak signal detection based on Duffing oscillator [C]//Information Management,Innovation Managemation and Industrial Engineering.Taipei:IEEE Conference,2008:430-433.
[9]夏均忠,刘远宏,冷永刚,等.微弱信号检测方法的现状分析[J].噪声与振动控制,2011,31(3):156-161.
[10]代理,李健,郑豫,等.基于双耦合Duffing振子的随机相位正弦信号检测[J].成都信息工程学院学报,2008,23(1):50-53.
[11]徐艳春,杨春玲.基于混沌振子的微弱信号检测技术研究[J].电气应用,2008,27(8):38-41.
[12]王凤利,马孝江.基于混沌的旋转机械故障诊断[J].大连理工大学学报,2003,43(5):36-639.
[13]吴参,李兴林,孙守迁,等.混沌理论在滚动轴承故障诊断中的应用[J].轴承,2013,12(1):60-64.
[14]李月,路鹏,杨宝俊,等.用一类特定的双耦合Duffing振子系统检测强色噪声背景中的周期信号[J].物理学报,2006,55(4):1672-1677.
[15]赵志宏,杨绍普.一种基于样本熵的轴承故障诊断方法[J].振动与冲击,2012,31(6):136-141.
Weak Fault Signal Detection Based on Coupled Duffing Oscillators
WANG Xiao-dong1,2,ZHAO Zhi-hong2,YANG Shao-pu1,2
(1.School of Mechanical Engineering,Shijiazhuang Tiedao University,Shijiazhuang 050043,China;2.Key Laboratory of Traffic Safety and Control of Hebei Province,Shijiazhuang 050043,China)
For the shortage of the traditional signal processing method in weak signal detection in low SNR condition,a new system detection method based on a double Duffing oscillator is proposed.Through dynamic analysis,this system is found to have a more complex dynamic behavior than that of the single Duffing oscillator.The principle of weak signal detection based on phase plane changing is expounded.Through transforming the time scale,the unknown frequency signals are detected.Finally,the weak pulse signal is detected and the early fault diagnosis of a real bearing is realized,and good results are obtained.This method has broad prospects for application in early fault diagnoses of wireless communications,radar systems and rotating machinery.
vibration and wave;bi-coupled Duffing oscillators;chaos;periodic signal;fault diagnosis
TH163.3
ADOI编码:10.3969/j.issn.1006-1335.2016.03.036
1006-1355(2016)03-0174-05+209
2015-11-05
国家自然科学基金资助项目(11172182;11227201;11472179)
王晓东(1989-),男,河北省沧州市人,硕士研究生,主要从事故障诊断与混沌理论研究。E-mail:wx_dong@126.com
