遭受水下爆炸的舰船缩比模型毁伤评估

程素秋，陈高杰，王树乐

遭受水下爆炸的舰船缩比模型毁伤评估

程素秋，陈高杰，王树乐

（中国人民解放军 海军91439部队，辽宁 大连 116041）

对某型舰船缩比模型遭受水下爆炸的弹塑性动力响应进行数值仿真与实爆试验研究，基于总纵强度毁伤和局部塑性变形的表征参数进行毁伤等级评估。结果表明，加速度响应和毁伤等级随冲击因子增大而增大，局部响应与船体振型相关，局部塑性变形毁伤等级最高时总纵强度毁伤等级并不是最高。研究成果可为实船爆炸试验评估提供参考。

振动与波；舰船缩比模型；水下爆炸；动力响应；数值模拟

遭受水下爆炸的舰船结构弹塑性动力响应研究对于提高现役舰船的生命力和战斗力，具有重要意义。因实船爆炸试验的巨额经费、超长周期和不可重复等特点，在实际研究中常用缩比模型爆炸试验来做先期研究。1984年，Rentz用试验手段研究加筋平板在水下爆炸作用下的动态响应，并进行了数值计算［1］。1988年，Gifford等对具有初始裂纹焊接厚板的动态响应作了一系列试验研究［2］。胡俊波等提出了改进型冲击因子的计算方法，并经某目标抗水下爆炸试验验证［3］。陈辉等利用整船缩比模型试验，得到冲击环境参数与水下爆炸载荷间的关系［4］。朱锡等对水面舰艇防雷舱结构模型进行了一系列水下抗爆能力试验［5］。张海鹏等研究对大缩尺比船模，使用畸变模型实现对原型总纵强度准确预测的方法［6］。秦健等基于π定律提出了在水下爆炸作用下加筋板模型动态响应的相似预报方法［7］。程素秋等对某典型舱段模型进行水下爆炸试验，研究了模型结构所遭受的载荷及其动态响应［8］。高浩鹏等设计了多层隔振系统用于水下爆炸试验时测量设备抗冲击防护［9］。张晓阳等采用频域法和时域法对液压螺栓有接触应力时抗冲击性能进行仿真［10］。

1　舰船缩比模型设计

以某型舰为母船，按总纵强度相似原则，对母船作简化，并忽略母船舰载设备对其质量分布的影响。缩比模型（以下简称船模）共分8个舱，缩比因子1：20，不另行配重。其中艏舱较长（是其它舱室的两倍长），其余舱室长度一样。船模共设7道横舱壁，2层平台和中纵舱壁，平台2与船底外底板组成双层底，双层底内还有两道纵旁舱壁加强，甲板、平台1、平台2的板厚4 mm，其余结构的板厚3 mm，模型结构总质量约m=429.4 kg，材料选用普通船用钢Q235；内部结构示意图见图1。两端分别设有水密间，可以保证模型在壳体破裂后仍能浮在水面。

图1　某型舰船缩比模型结构剖面图

2　数值仿真研究

2.1有限元模型建立

计算时考虑重力因素和壳板的应变率强化效应。有限元模型中船体网格由59 034个壳单元（S4R）组成，水域网格由3 615 054个声学单元（AC3D8R）组成。结构与水域间用TIE约束法模拟流固耦合，采用ABAQUS/EXPLICIT求解器（声固耦合法）计算。船模和外部水域的有限元模型分别如图2、图3所示。

图2　结构有限元模型

图3　流体模型图

图4　Q235钢的动态力学性能参数

通过拟合得到：D=271.6，取ρ=7 800 kg/m3。E=2.1×1011Pa，材料极限应变取εf=0.3。

炸药采用 Jones-Wilkins-Lee（JWL）状态方程［12］。JWL描述爆压P和单位体积内能e及爆炸产物体积V之间的关系，即

式中 A=373.77 GPa；B=3.747 1 GPa；R1=4.15；R2=0.9；ω=0.35；η=ρ/ρ0、ρ0=1.63 g/cm3、ρ为爆炸产物密度；TNT的e=6.0 GJ/m3。爆速为6 930 m/ s，爆压为21 GPa。

2.2计算工况

取计算工况和实爆试验工况完全相同。船模爆炸试验是在某海域的近海岸完成，试验场景如图7所示。炸药为1 kg RDX球形药包和6 kg TNT球形药包。对船模进行了七次水下爆炸，每次试验时选用的药包、布放距离、龙骨冲击因子详见表1，最后一次为毁伤试验，没有进行测量。

表1　船模计算工况表

2.3船模测点分布

船模上布设包括自由场压力、加速度和应变等测点。试验前在船模上要按照预定位置装好传感器。加速度、应变测点位置及标号如图5、图6所示，应变片贴在平台1与平台2间的内壁上。

图5　平台2加速度测点位置

图6　底部加速度测点位置

图7　船模爆炸试验场景

3　船模结构弹塑性动力响应分析

3.1水下爆炸冲击波载荷分析

Cole和Zamyshlyayev相继提出了计算水下冲击波载荷的经验公式（2）与（3），来计算冲击波压力P（t）、峰值压力Pm等。其中：W为药量/kg，R为爆心距观测点的距离/m，R0为药包的初始半径/m，早期的冲击波以指数形式衰减，当t＞θ以后，冲击波的衰减变慢，以近似于时间倒数的关系衰减。

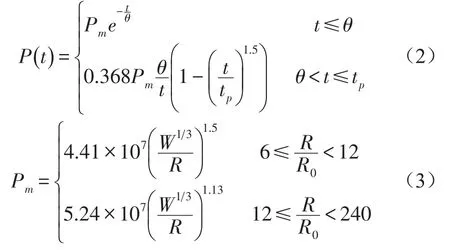
图8和图9表示自由场压力曲线，图中是实测曲线与计算曲线的对比，二者趋势基本相符，但实测曲线较计算曲线更复杂，所包含的载荷更丰富，反映了自由面截断和海底反射效应（注：工况3与工况4选择工况3；工况5与工况6选择工况5）。自由场压力峰值对比见表2。

图8　仿真计算与实爆试验的自由场压力对比

3.2船模在水下爆炸作用下的动响应规律

船模爆炸试验的冲击因子是按照炸药当量由小到大，爆距从远及近的原则而设计的，为便于对比，前三次试验使用相同的药包，后三次试验药包一样。另外，工况1和工况2、工况3和工况4的冲击因子基本相同，工况5和工况6只是药包距船模水平距离不同；工况3和工况5只是药包TNT当量不同，这是为考察单一因素作用下的船模动响应规律而设置的。

从表3中数据可知，同一测点在相同冲击因子作用下的响应也是有差异的，工况2、4中各测点响应值明显高于工况1、3（个别值偏离大的是因其零漂现象引起的）；同一工况中各测点的动响应也是不同的，离爆源越近，响应值越大，由于药包布放时偏向船模首部，因此首部测点的响应值要大于尾部测点；距离爆源位置差不多时，船模底部中间处的响应值要大于首尾两端及1/4处；平台2上的响应要小于底部。这是由于舰船是具有结构振型的，初始传递到船底的冲击波作为船底动能的一部分，以刚体运动的形式出现，其余爆炸能量则引起舰船结构以不同结构振型作振荡变形。当冲击能量在船体结构中向上传播时，高频分量会因结构振型的作用而衰减，而低频振型的响应就变得更加突出。

图9　测点BOTTOM-2-L在各次工况中的加速度时间历程比对

4　船模结构在水下爆炸作用下的毁伤评估

水面舰船在水下爆炸作用下的毁伤，可分为总体毁伤和局部毁伤。总体毁伤又分为：总纵强度毁伤和剩余总纵强度毁伤。前者是由中近场大当量水

下冲击波和气泡脉动压力作用下舰艇结构产生鞭状运动、及近距爆炸产生的冲击振动与底部负压区使舰艇产生中垂状态的迭加作用等引起。后者是在接触爆炸作用下造成舰艇的局部破口，引起舰艇结构间接的总体毁伤，属于舰艇结构破损剩余强度。水面舰船局部毁伤又可分为：局部破损毁伤和局部塑性变形毁伤。前者是由近距或接触爆炸作用下引起

的；后者是由非接触爆炸作用下引起的。针对表1所列的工况，船模的毁伤形式有两种：总纵强度毁伤和局部塑性变形毁伤。

表2　自由场压力峰值对比

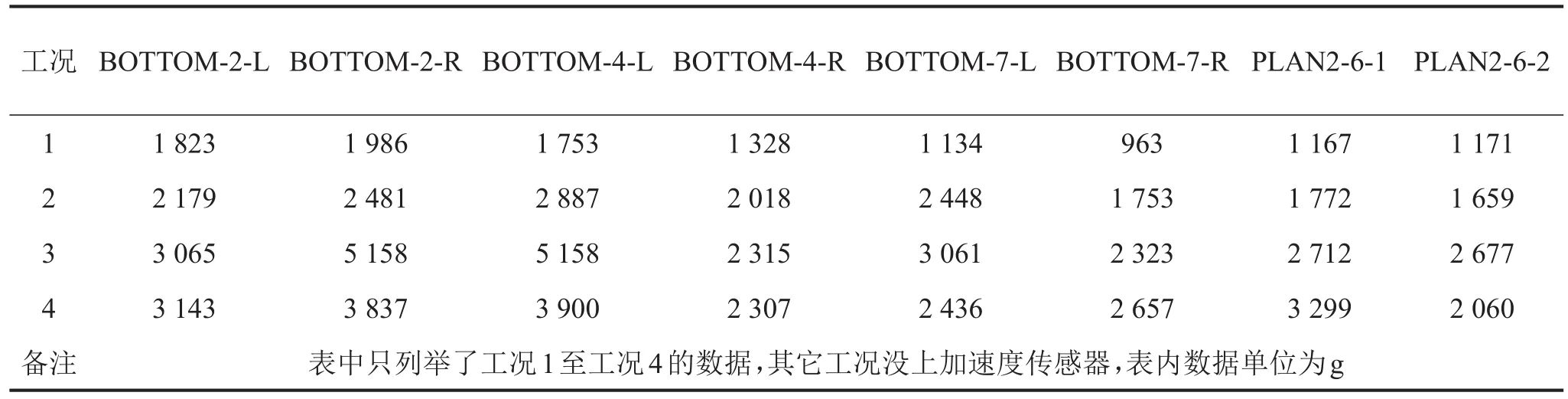
表3　船模爆炸试验的加速度峰值统计

4.1总纵强度毁伤计算

式中Mu1为完好船体梁计算剖面弹性极限弯矩值；Mq1为计算状态对应的船体梁剖面所受静、动外力合成作用弯矩的最大设计值。即

其中Ms1为完好舰艇静水弯矩值，Me1为气泡载荷附加弯矩值，Md1为最大设计冲击振动弯矩值。

4.2局部塑性变形毁伤计算

假设加筋板结构为四周固支，在爆炸载荷作用下加筋板结构发生大挠度变形，考虑到结构边界产生塑性铰线，最终变形的挠曲面可近似为正弦曲面。其挠曲面函数可取为

（1）板架边界塑性铰弯曲变形能U1

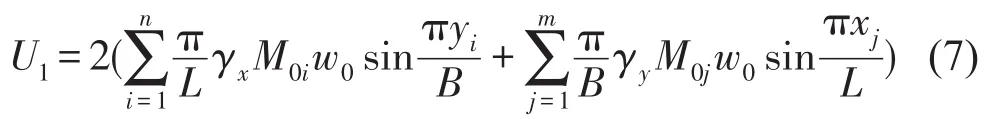
（2）板架弯曲变形能U2

（3）板架伸长变形能U3

（4）结构初始动能Ek

相对于结构响应时间，冲击波持续时间非常短，可近似认为炸药的冲击波能全部被结构吸收。在非接触水下爆炸条件下，可假设冲击波为平面波，由冲击波的能流密度表达式得到结构吸收的冲击波能，即冲击波作用后结构的初始动能

（6）能量守恒原理

根据能量守恒原理有U1+U2+U3=Ek。将式（6）—式（10）和参数代入，进行求解可以得到中心挠度w0，进而可以得到整个加筋板结构的变形场。即

4.3局部塑性变形算例分析

实爆试验结果表明，舷侧板架（上）的变形较严重，因此取该板架作为局部挠曲变形的分析对象。

对比表4和表5，发现同一工况针对不同参数的评估结果是不同的。评估时针对不同参数可分别作结论，然后综合全部评估结果衡量后得出在某个冲击因子下会达到的效果及量级。图10是工况7的数值模拟与实爆试验的塑性变形对比。对比图中由变形情况可知，数值模拟与实爆试验结果基本相符。

表4　船模总纵强度抗毁伤等级评估结果

表5　舷侧板架局部挠曲变形毁伤等级评估结果

图10　船模在工况7后的塑性变形对比

5　结语

对某型舰船缩比模型遭受水下爆炸时的弹塑性动力响应进行数值仿真与一系列实爆试验研究。基于总纵强度毁伤和局部塑性变形对该模型进行了毁伤评估。结果表明，加速度响应和毁伤等级随冲击因子增大而增大，局部响应与船体振型相关，局部塑性变形毁伤等级最高时总纵强度毁伤等级并不是最高。研究成果可为实船爆炸试验评估提供参考。

［1］RENTZ T R.An experimental investigation into the dynamicresponseofastiffenedflatplateloaded impulsively by an underwater shockwave，A123151［R］. 1984.

［2］GIFFORD L N，CARLBERG J R，WIGGS A J，et al. Explosive testing of full thickness precracked weldments ［J］.ASTM Special Technical Publication，1990（1074）：157-177.

［3］胡俊波，张志华，李庆民，等.水下爆炸对水下目标的毁伤评估研究［J］.振动与冲击，2010，29（10）：206-210.

［4］陈辉，李玉节，潘建强，等.水下爆炸条件下不同装药对水面舰船冲击环境的影响试验研究［J］.振动与冲击，2011，30（7）：16-20.

［5］朱锡，张振华，刘润泉，等.水面舰艇舷侧防雷舱结构模型抗爆试验研究［J］.爆炸与冲击，2004，24（2）：133-139.

［6］张海鹏，岳永威，苏罗青，等.水下爆炸作用下舰船总纵强度模型实验方案研究［J］.振动与冲击，2012，31（6）：175-180.

［7］秦健，张振华.原型和模型不同材料时加筋板冲击动态响应的相似预报方法［J］.爆炸与冲击，2010，30（5）：511-516.

［8］程素秋，樊宝顺，薛飞，等.水下非接触爆炸作用下舱段模型的动态响应［J］.爆炸与冲击，2008，28（4）：360-365.

［9］高浩鹏，黄映云，金辉，等.水下爆炸作用下多层隔振系统动态特性分析［J］.噪声与振动控制，2015，35（3）：186-188.

［10］张晓阳，陈汝刚，解忠良，等.舰船轴系用液压螺栓抗冲击性能的数值仿真［J］.噪声与振动控制，2015，35（4）：149-152.

Damage Evaluation of a Ship Scaled Model Subjected to Underwater Explosion

CHENG Su-qiu，CHEN Gao-jie，WANG Shu-le
（91439 Unit of PLA，Dalian 116041，Liaoning China）

The dynamic response of a ship scaled model subjected to underwater explosion is studied using numerical simulation and realistic explosion tests.Based on the characteristic parameters of longitudinal strength and local plastic distortion，the grade evaluation of anti-deflection capability of the model is conducted.The results show that the acceleration response and damage grade increase with the shock factors，and the local response is related to the vibration mode.When the damage grade based on the local plastic distortion reaches the highest value，the damage grade based on longitudinal strength is not necessarily the highest.The result is of significance for evaluation of ship shock tests.

vibration and wave；ship scaled model；underwater explosion；dynamic response；numerical simulation

U663.85

ADOI编码：10.3969/j.issn.1006-1335.2016.03.015

1006-1355（2016）03-0070-06

2015-06-10

程素秋（1968-），辽宁省丹东市，女，硕士，高级工程师，从事水下爆炸试验仿真与评估工作。E-mail：csq4028@sina.com