变截面管道流噪声数值计算

赵　威，彭　旭，陈　明，李　奇

变截面管道流噪声数值计算

赵威1，彭旭1，陈明1，李奇2

（1.武汉第二船舶设计研究所，武汉 430064； 2.上海海基盛元信息科技有限公司，上海 200235）

采用变分形式的Lighthill声类比方程来定量地求解管路内流噪声。数值计算主要分为两步：第一步通过精细的流场网格计算非定常的噪声源；第二步将声源结果守恒插值至声学网格，并通过有限元法计算声传播。在非定常流场计算中采用大涡模拟（LES）湍流模型，以获取噪声源。与试验值对比发现数值计算结果与试验结果趋势一致，从而验证了计算结果的合理性。研究结果表明，在分析原截面突缩管的主要噪声源分布后，优化管截面获得很好的降噪效果。

声学；流噪声；Lighthill声类比方程；有限元法；大涡模拟；湍流模型

在管道系统中各种阀、变径管和管路分支是管路系统中主要流噪声源，但是有关这些部件的流噪声研究比较少。随着减振降噪要求的提高，越来越多的研究者开始关注管路中流噪声的数值计算和试验研究。由于噪声试验研究花费高、试验周期长以及环境要求高，往往很难在工程实际中得到准确的试验结果。近些年来随着数值计算方法的发展和数值计算能力的提高，采用数值计算方法研究流噪声成为了一个重要手段。由于积分形式的数值算法采用了许多假设（比如紧致声源、自由远场），会使得管内声场的计算结果存在较大误差。有限元法对整个声源域进行离散处理，可以很方便地处理近场或封闭域内的噪声。因此，本文采用基于有限元的变分形式Lighthill方程来数值求解变截面管的流噪声。

基于有限元变分形式Lighthill方程对整个噪声源进行离散，可以很方便地研究流场中的噪声源分布及发声机理。目前，国内外有关变分法计算流噪声的相关文献还比较少。Oberai首次采用变分形式的Lighthill声类比方程计算机翼噪声，并与Curle的理论结果吻合得很好［1］。耿冬寒采用大涡模拟LES+基于有限元/无限元的变分形式的Lighthill声类比方程求解空腔水动力噪声［2］。Kaltenbacher采用LES和SAS两种湍流模型计算了半自由声场中立柱扰动的声场，与试验值吻合得很好［3］。杨晓宇采用CFD/CAA混合数值分析了高速列车风噪声［4］。王超采用LES和声学无限元方法耦合求解得到潜艇的声压级，与边界元法求得的结果相似［5］。通过与理论解或试验值对比，这些研究均表明变分形式的Lighthill方程能准确地得到声场信息。

本文采用参考文献［6-7］中变截面管的模型，文献中所得到的流噪声仅仅只是流场压力脉动即通常意义上所称的“伪声”，并不能准确反映声场信息。在此基础上定量地计算整个管路中流噪声，并根据噪声发声机理来采取降噪措施。文中采用二维大涡方法计算了变截面管道的流场，然后将流场结果导入声学软件中提取时域声源并转化为频域声源，最后计算声源在整个管段中的传播。为了检验计算结果的准确性，与试验测量值进行了比，发现两者之间趋势一致。在分析噪声机理后，对管段进行了优化。

1　变分形式的Lighthill声类比方程

Lighthill声类比方程采用有限元离散［8，9］分部积分重新整理后，得到有限元变分离散弱解形式

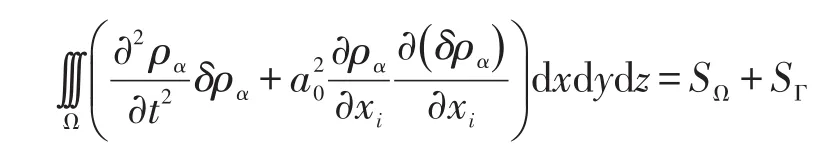
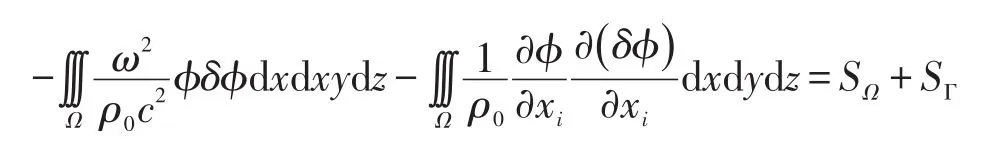
其中，右边第一项为体声源项为

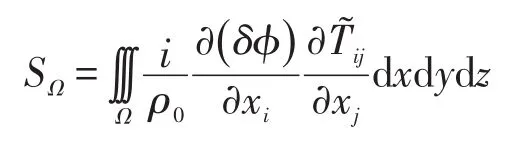
而右边第二项为面声源

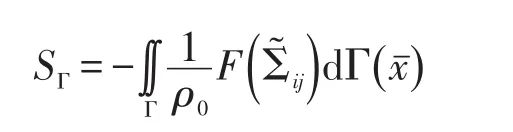
在本文的研究中由于是高雷诺数湍流流场，流场动能主要由大涡携带，对流效应/惯性作用主导流场，涡源项ρViVj为主要声源，黏性源项相对较小可以忽略。远离声源处由于湍流脉动很小可以忽略，而固体表面处的速度脉动为零，因此面声源项为零。由于数值计算中流场网格和声学网格尺度相差很大，为了保证能量守恒将声源结果守恒插值至声学网格。

2　数值计算模型

本文所研究的截面突缩管属于轴对称结构，故而采用二维流场模型来计算其流场，如图1。模型突缩管段长0.6 m，直径为0.1 m。入口段管长0.5 m，出口段管长7 m，管径为0.2 m。在流场计算中由于是低马赫数，可以作为不可压缩流计算。为了精确计算流场，壁面Y+值达到1，网格总量为57万。进口采用速度进口条件，出口采用压力出口，壁面为无滑移壁面。计算湍流模型分别为定常采用k-ε模型，非定常采用LES模型。计算工况根据文献［7］中所测试工况，进口速度分别为16 m/s、23 m/s、30 m/s。在定常计算收敛后，以定常计算值作为初始值计算非定常流场，为了提高数值计算精度，残差控制在10-5以下。非定常计算趋于稳定后，取4×10-4s间隔时间步1 250步计算结果并存储。根据傅里叶变换可知，得到的频域值的频率分辨率为2 Hz。

在计算得到流场结果后，提取时域声源信号并转换为频域的声源信号，最后在频域内计算整个声场结果。如图1（b）在声学计算模型中，为了保证一个波长内至少有8个单元，网格最大尺寸为0.008 m，网格总量为14万。将整个计算域分为了两个部分：一部分为声源区，浅色部分，另一部分为声传播区，深色部分。在管路的外端处设置声导纳边界条件以模拟无限长管道。同时为了减小声源区边界处由于截断产生的虚假声，采用了余弦滤波函数除去了虚假声的影响。为了与文献［7］中的试验测试结果对比，在模型同样的位置也设置了相应的监测点如图1。

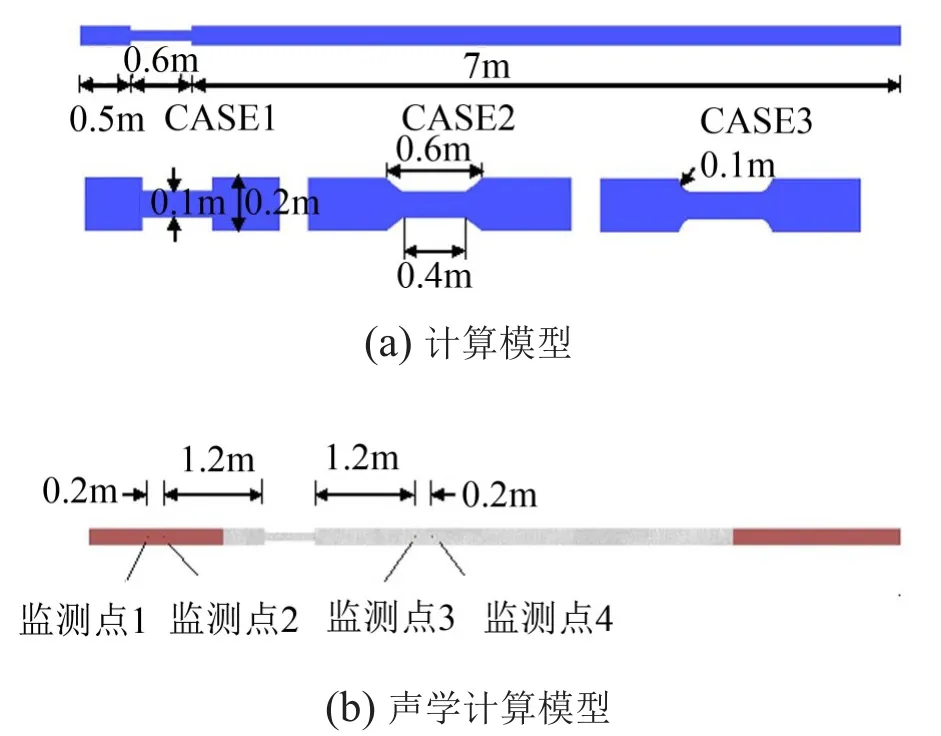
图1　变截面管的计算模型和声学计算模型

3　计算结果分析

原模型三种工况不同频率下的声源强度分布如图2—图4。在突缩管中生成的湍流噪声为宽频噪声，图中给出了50 Hz、100 Hz、200 Hz和500 Hz时声源强度分布，主要噪声源位于声源区内，在截断面没有噪声源。从图中可以看出，随着速度的增大，最大声源强度明显地增大。主要声源为突缩管入口处回流区涡脱落在突缩管段形成的噪声源。突缩管的出口处由于射流引起管两边的回流也形成了一定强度的噪声源，但是当频率增大后，该部分噪声源的强度明显降低了。根据Powell、Howe的涡声理论［8-9］，流场中涡的拉伸、变形、消散和溃灭均会产生声，而流场中涡的分布恰与主要声源分布一致，由此可以说明声源提取是正确的。

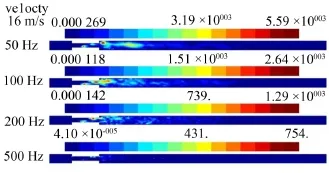
图2　不同频率下CASE 1的声源强度分布图（速度为16 m/s）

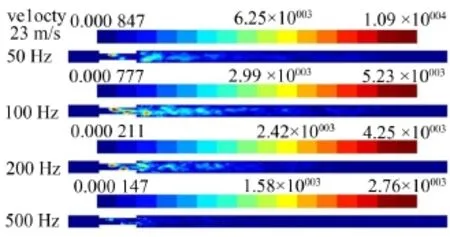
图3　不同频率下CASE 1的声源强度分布图（速度为23 m/s）

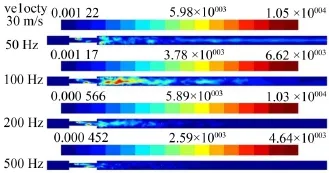
图4　不同频率下CASE 1的声源强度分布图（速度为30 m/s）

图5给出了CASE 1下不同进口速度时数值计算监测点处声压级与试验值的对比。从图中可以看出，数值计算结果为宽频噪声且随着频率的增大而减小，数值计算值与试验值的声压级频谱曲线在趋势上一致。上下游两个监测点声压级的数值计算值比试验值要大，说明二维大涡模型计算使得流噪声有偏差，主要是管内流的三维效应明显，周向相位不一致，而二维计算仅取某个局部计算值，造成结果偏大；其次由于声场为静止的而没有考虑非均匀流场对声传播的折射影响。在上游监测点的低频段，试验值要大于仿真值，并且出现了峰值频率，可能与试验过程中引入风机噪声有关，从而使得噪声值偏大。但是，在下游监测点，由于正处于声源区内，整个曲线的趋势和量级与试验都吻合得更好。

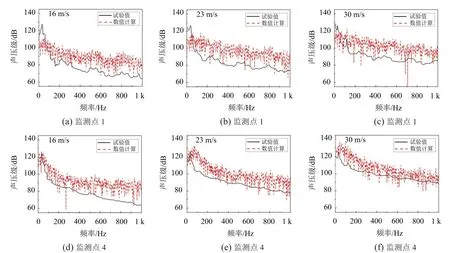
图5　截面突缩管内流噪声数值计算结果与试验结果比较

在分析整理原来的截面突缩管主要噪声源后，试图通过改变截面形式来降低噪声。因此，提出了两种优化方案，具体结构如图1所示，CASE 2采用锥形过渡，CASE 3采用圆弧过渡。优化后两种模型的频域声源强度分布如图6和图7。从图中可以看出，主要的噪声源为突缩管出口处射流引起的回流形成，进口处突缩管由于渐进过渡减小了截面突变形成的回流涡脉动。对比原模型突缩管段由于涡脱落产生的噪声源强度，优化后最大声源强度要小得多。

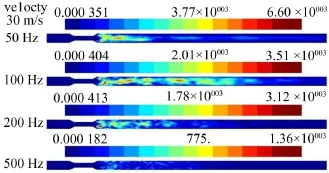
图6　不同频率下CASE 2的声源强度分布图（速度为30 m/s）

图7　不同频率下CASE 3的声源强度分布图（速度为30 m/s）

优化之后的模型与原模型监测点处声压级对比如图8，图中进口速度为30 m/s。从图中可以明显看出，优化后的模型噪声降低了，而且圆角过渡的模型要更好一些，在高频处相对于原模型噪声减小可达20 dB。在上游监测点处，整个频段上两种优化模型的噪声都有所降低；而在下游处，低频段降噪不明显，高频段有很明显的降噪效果。相对于进口处监测点，出口监测点在0～300 Hz的频段有一个快速下降的趋势，之后便趋于平稳。由图4的声源强度图可知，低频段的高声压级是由于突缩管出口处射流噪声源影响；当频率高于300 Hz之后，由于射流噪声源强度减弱使得声压级也降低。

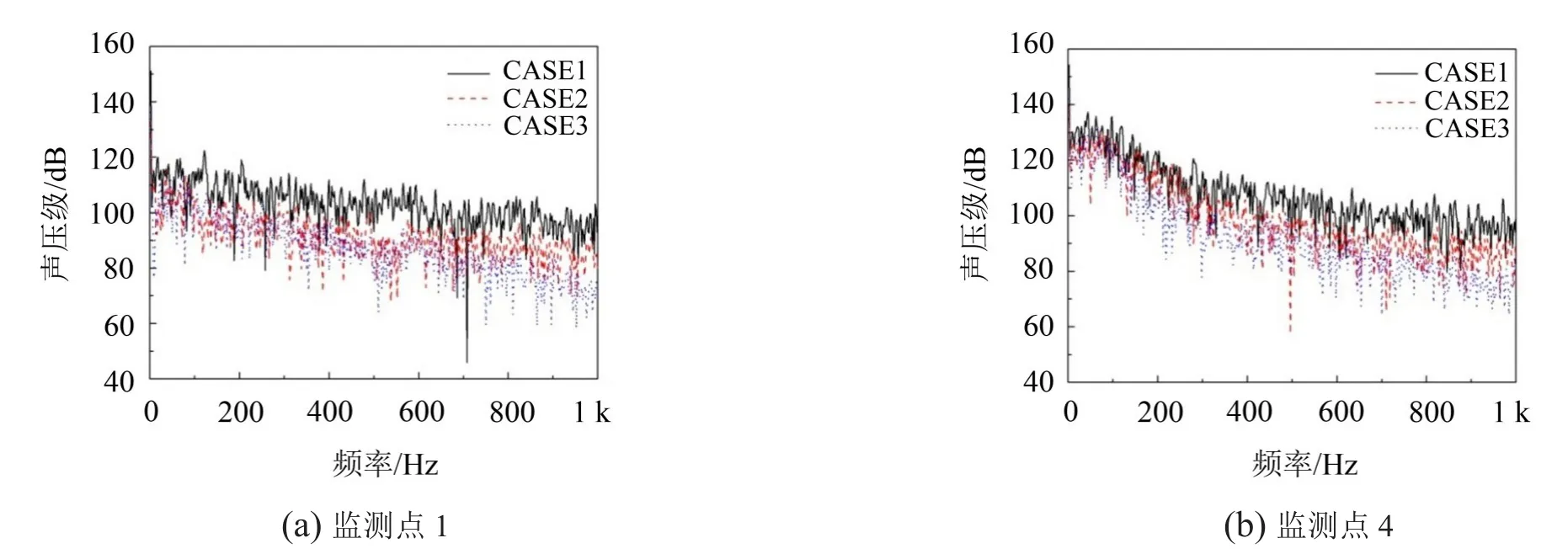
图8　不同工况下监测点处的声压级频谱图

各个监测点处的总声压级如表1所示，可明显地看出优化后的模型声压级降低了，而且上游的声压级降低更为突出，降低幅值可达10 dB。CASE 2 和CASE 3两种优化模型之间的上下游监测点总声压级相差不大（小于3 dB），说明在总能量上来看两者优化效果一样。但是从图8可以看出在500 Hz以上的频段，CASE 3的声压级明显比CASE 2要小，有的频段甚至达15 dB以上。

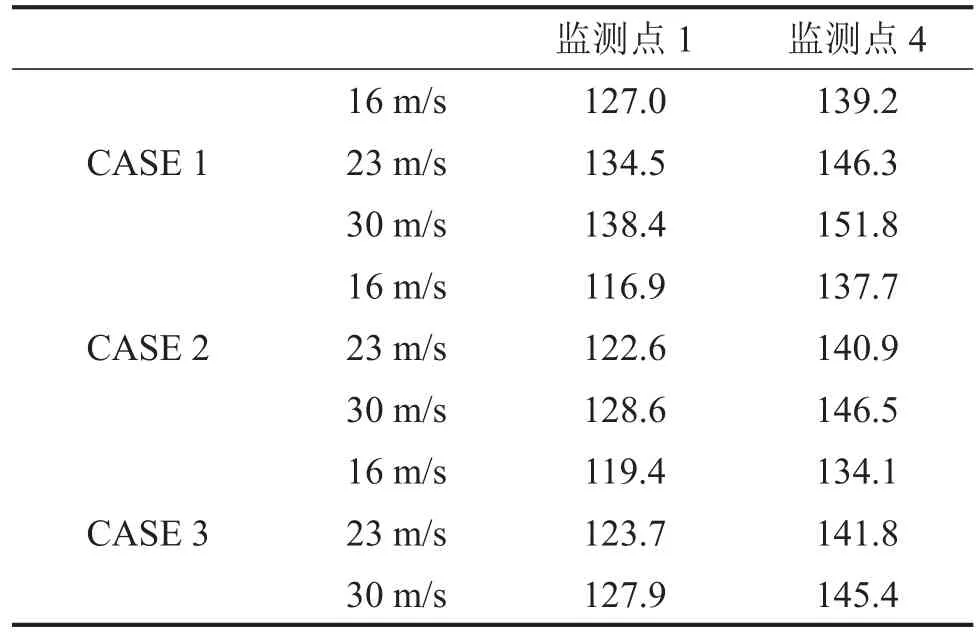
表1　监测点处的声压级总级（dB）对比

4　结语

本文采用变分形式Lighthill声类比方程计算了截面突缩管的流噪声。通过分析截面突缩管主要噪声源的分布确定了优化形式，并分析了优化模型的计算结果。

（1）通过与试验对比，发现二维计算得到的结果基本上与试验值趋势相符合，由此说明了二维计算的可靠性。但是在量级上由于二维大涡计算的简化以及未考虑流场的折射影响，使得数值计算结果有些偏大。

（2）分析突缩管内主要噪声源：入口处流体分离生成的涡脱落从而产生了主要噪声源，突缩管出口处的射流回流区也产生了一定强度的噪声源。

（3）通过管内的声源强度分布了解管内的主要噪声源，然后有针对性地改变管路模型，提出两种优化模型都有很好的降噪效果。但是对于工程实际来说锥形管过渡更易加工，可作为最好优化方案。基于有限元方法的声学计算方法为以后定量分析噪声源并进行有针对性的降噪提供了方法。

［1］OBERAI A A，ROKNALDIN F，HUGHES T J R. Computationalproceduresfordeterminingstructuralacousticresponseduetohydrodynamicsources［J］. ComputerMethodsinAppliedMechanicsand Engineering，2000，190（3-4）：345-361.

［2］耿冬寒，刘正先.大涡模拟-Lighthill等效声源法的空腔水动噪声预测［J］.哈尔滨工程大学学报，2010（2）：182-187.

［3］KALTENBACHER M，ESCOBAR M，BECKER S，et al. Numerical simulation of flow-induced noise using LES/ SAS and Lighthill's acoustic analogy［J］.International Journal for Numerical Methods in Fluids，2010，63（9）：1103-1122.

［4］杨晓宇，高阳.高速列车气动噪声Lighthill声类比的有限元分析［J］.噪声与振动控制，2011，31（4）：80-84.

［5］王超，郑小龙.用LES和无限元耦合方法预报潜艇流噪声［J］.噪声与振动控制，2015，35（1）：1-6.

［6］吕景伟，季振林.变截面管道内流噪声预报与实验测量［J］.噪声与振动控制，2011，31（1）：166-169.

［7］吕景伟.变截面管道内流噪声预报与实验测量研究［D］.哈尔滨：哈尔滨工程大学，2010.

［8］POWELL A.Theory of vortex sound［J］.The Journal of theAcoustical Society ofAmerica.1964，36（1）：177-195.

［9］HOWE M S.Theory of vortex sound［M］.Cambridge：Cambridge University Press，2003.

Numerical Simulation of Flow-induced Noise in the Pipelines with Variable Cross-sections

ZHAOWei1，PENGXu1，CHENMing1，LIQi2
（1.Wuhan Second Ship Design and Research Institute，Wuhan 430064，China；2.Shanghai Hikey-Sheenray Information Technology Co.Ltd.，Shanghai 200235，China）

The flow-induced noise in pipelines is simulated using the variational formulations of Lighthill acoustic analogy.Simulation of the flow-induced noise includes two-steps：（1）calculating the unsteady flow noise sources through the refined flow field grid；（2）using the interpolation method to the results of the noise source simulation to determine the acoustic nodal sources of the acoustic grid，and then calculating the acoustic propagation by means of the finite element method（FEM）.The large-eddy simulation（LES）turbulence model is employed in unsteady flow computation to find the acoustic sources.The numerical results of the acoustic pressure for the pipelines with variable cross-sections are compared with the experimental data.It is found that they are in good agreement.It is indicated that after analyzing the distribution of the acoustic source magnitude in the suddenly-contracted pipeline，the proposed optimal models perform well for noise reduction.

acoustics；flow-induced noise；Lighthill acoustic analogy；FEM；（large-eddy simulation）（LES）；turbulence model

TB533

ADOI编码：10.3969/j.issn.1006-1335.2016.03.010

1006-1355（2016）03-0048-04+150

2015-05-08

赵威（1987-），男，湖北荆门人，博士生，主要研究方向为振动与流噪声。E-mail：xyzwei159@126.com