基于微观尺度的砂土剪切波速度

黄博，夏唐代，周新民，刘志军



基于微观尺度的砂土剪切波速度

黄博1, 2，夏唐代1, 2，周新民3，刘志军1, 2

(1. 浙江大学滨海和城市岩土工程研究中心，浙江杭州，310058；2. 浙江大学软弱土与环境土工教育部重点实验室，浙江杭州，310058；3. 浙江省地震局，浙江杭州，310013)

运用宏观等效与微观接触理论相结合的方法研究砂土剪切波速度。在宏观上将砂土看作均匀连续各向同性介质，在微观尺度上假设砂土为等效球体半径相等、材料性质相同、随机堆积的固体颗粒的集合体，结合颗粒接触理论，引入颗粒形状修正系数，推导出砂土的等效剪切模量和宏观剪切波速度公式。通过定量计算进行参数分析。研究结果表明：孔隙比、砂土颗粒弹性模量、埋深和颗粒形状修正系数对砂土剪切波速的影响显著；有效内摩擦角、砂土颗粒泊松比、砂土密度和与配位数有关的常数对剪切波速影响较小。将理论计算结果与实测值进行对比，吻合较好，验证了本方法的可行性与正确性。

颗粒接触；颗粒形状修正系数；等效球体；等效剪切模量

剪切波速是土体的一个重要动力学参数，砂土介质中流固耦合更少，因此，砂土介质的剪切波速更能表征砂土的结构性，反映砂土颗粒排列和联结特征[1]。剪切波速也是砂土抗液化性能的重要指标，可用剪切波速对砂土抗震液化进行判别[2−4]。目前针对介质中的弹性波传播问题，主要是从宏观和微观2个尺度进行研究。从宏观尺度研究的主要成果有：Biot饱和多孔介质波传播理论、Kuster的散射波分析法和Carroll-Katsube的力学响应分析等[5]。这些宏观理论忽略了砂土颗粒间的接触力学行为，对砂土结构性的反映有限。微观尺度研究主要是从微观的颗粒入手，基于散粒体微观颗粒接触理论，研究颗粒间微观作用力，通过建立微观作用与宏观作用之间的联系，最终探求弹性波传播问题。BRANDT等[6]结合Hertz颗粒接触模型提出了最早的土中波的颗粒模型分析法。近年来，随着多位学者对颗粒接触理论[7−9]以及散粒体细观力学变量与宏观变量关系研究[10]的逐步深入，基于微观尺度的弹性波传播理论研究越来越受到重视[11]。本文作者在宏观上将砂土视为均匀连续各向同性介质，根据微观理论模型中的颗粒接触理论，引入颗粒形状修正系数，推导砂土等效剪切模量，再代入宏观等效模型，得到剪切波波速计算公式，分析有效内摩擦角、土密度、孔隙比、砂土颗粒弹性参数、埋深和颗粒形状修正系数等因素对剪切波速的影响。最后通过工程实测算例对本文方法进行验证。

1 宏观剪切波速

砂土介质本质是非均匀的，一般认为是由随机堆积的微小砂颗粒以及填充于颗粒间空隙内的液相与气相组成的集合体。但从工程勘探的角度来看，弹性波波长远大于砂颗粒粒径，同时也是颗粒空隙尺度的无穷大量级，因此，在宏观尺度上，仍然可以采用等效连续介质理论来描述砂土介质的波动行为。将砂土在宏观上看作均匀连续各向同性介质，弹性波传播的波动方程为

式中：为弹性波波速；为质点位移。

经推导，宏观尺度上，砂土介质中剪切波速s为

式中：为砂土介质等效剪切模量；为密度。

砂土介质是由固、液、气3相组成，由于流体不抗剪，因此，可以假设砂土等效剪切模量为干燥状态下砂土介质中固相砂土颗粒骨架的等效剪切模量，则砂土宏观剪切波速公式为

式中：s为颗粒骨架的等效剪切模量。

2 微观接触模型

砂土颗粒的细观组构、排列及形状等因素会影响砂土颗粒骨架的等效剪切模量。假设砂土介质中由砂颗粒构成的固相为等效球体半径相等、材料性质相同、随机堆积的固体颗粒的集合体。根据式(3)，通过推导砂土颗粒骨架的等效剪切模量的表达式，最终求得砂土剪切波速公式。

周志军等[12]引入颗粒形状修正系数来描述任意形状颗粒与等效后的球形颗粒半径之间的差异，并研究了散粒体的微观组构与本构关系，得到散粒体等效剪切模量表达式为

式中：为等效球形颗粒的半径；为散粒体孔隙比；D为等效球形颗粒法向接触刚度；s为等效球形颗粒切向接触刚度；为形状修正系数；m为常数，与配位数有关。

将砂土颗粒看作半径相同的球体，在颗粒总数不变的情况下，球体总体积等于原砂土颗粒总体积时，该球体称为砂土颗粒的等效球体，该半径称为砂土颗粒的等效球形半径。

在颗粒接触理论中，平均每个颗粒与其他颗粒接触的点数称为配位数。周志军等[13]研究发现，配位数与孔隙比满足关系：

式中：m为常数，一般为11.5~15.6，均值为13.4。

王平等[14]提出颗粒形状修正系数的概念。定义为颗粒中心到表面任一接触点方向上的径向矢量，其中和为球坐标，则该点径向矢量的相对分布为

令颗粒表面所有接触点径向矢量相对分布的平均值为，则对同一颗粒而言，其值不随单位法向矢量的改变而变，为定值，只与颗粒表面形状有关。即为颗粒的形状修正系数。对散粒体全部颗粒的形状修正系数取平均，即为该散粒体的形状修正系数。

根据Hertz模型[15]，2个等径接触等球体的法向接触刚度D与法向压缩接触面积可分别表示为：

MINDLIN[16]在Hertz模型基础上推导出2个等径球体弹性正向接触时的切向刚度：

DIGBY[17]为将微观尺度下等球体法向接触力与宏观力建立联系，假设随机堆积的等球体外包络面外侧均匀分布着围压0，则

将式(5)代入式(10)得

将式(7)，(8)，(9)和(11)代入式(4)得到砂土颗粒骨架的等效剪切模量的表达式：

将式(12)代入式(3)，得到砂土剪切波速表达式：

刘瑜[18]认为可将砂土颗粒所处状态下的平均有效应力看作围压0，则

而静止条件下水平方向与竖直方向土压力可表示为：

当无附加荷载，即=0时，

3 参数分析

通过定量计算对式(18)中各参数对剪切波速的影响进行分析。在分析某一参数的影响时，将该参数视为变量，其他参数视为常量。参数为常量时，结合实际工程应用，取值如表1所示。

表1 计算参数取值

Table 1 Values of parameters

图1所示为在不同有效内摩擦角条件下孔隙比对剪切波速的影响曲线。从图1可见：剪切波速s随孔隙比的增大而减小，当从0.2增大到1.0时，s减小了28.86%，说明孔隙比对剪切波速影响显著。从图1还可见：剪切波速s随有效内摩擦角′的增大而减小，但当′从25°增大到40°时，s仅减小了4.98%，说明砂土有效内摩擦角对剪切波速影响很小。

φ′/(°)：1—25；2—30；3—35；4—40。

图2所示为在不同泊松比条件下颗粒弹性模量对剪切波速的影响曲线。从图2可见：剪切波速s随砂土颗粒弹性模量e的增大而增大，当e从5 GPa增大到30 GPa时，s增大了81.71%，说明砂土颗粒弹性模量对剪切波速影响显著。从图2还可见，剪切波速s基本不随砂土颗粒泊松比的变化而变化，说明砂土颗粒泊松比对剪切波速影响很小。

：1—0.20；2—0.25；3—0.30；4—0.35。

图3所示为在不同的m下埋深对剪切波速的影响曲线。从图3可见：剪切波速s随埋深的增大而增大，当从10 m增大到50 m时，s增大了28.97%，说明埋深对剪切波速影响显著。从图3还可见：剪切波速s随与配位数有关的常数m的增大而增大，当m从11.5增大到15.5时，s增大了10.46%，说明与配位数有关的常数m对剪切波速影响较小。

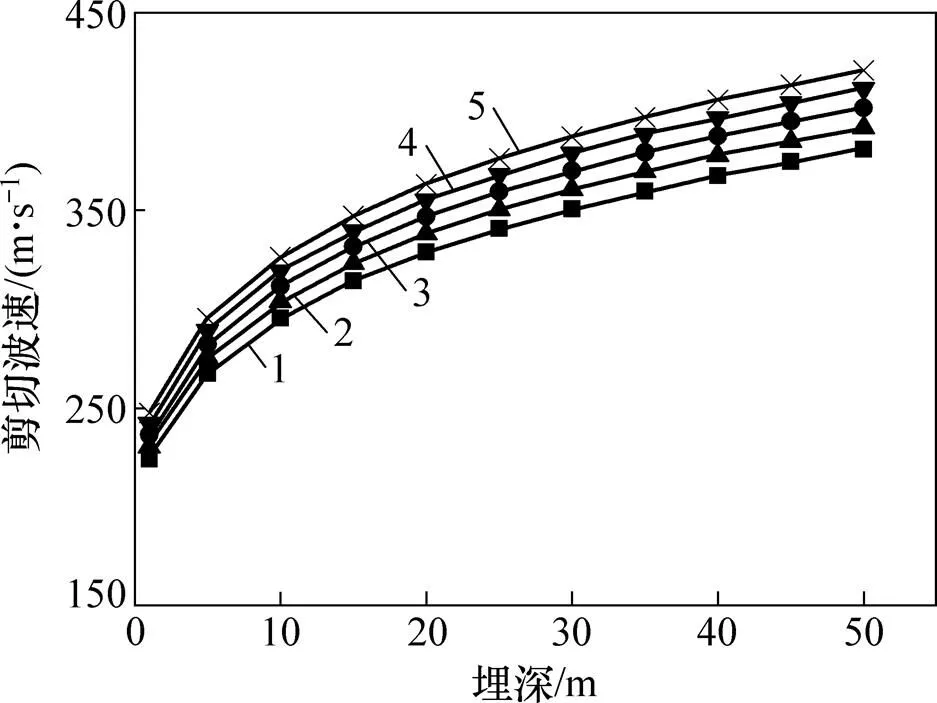
Cm：1—11.5；2—12.5；3—13.5；4—14.5；5—15.5。

图4所示为在不同土层密度条件下颗粒形状修正系数对剪切波速的影响曲线。从图4可见：剪切波速s随颗粒形状修正系数的增大而增大，当从0.2增大到1.0时，s增大了123.61%，说明颗粒形状修正系数对剪切波速影响显著。从图4还可见：剪切波速s随土层密度的增大而减小，但当土层密度从1.75g/cm3增大到2.05 g/cm3时，s仅减小了5.38%，这说明在常见密度范围内，土层密度对剪切波速影响很小。

ρ/(g∙cm−3)：1—1.75；2—1.85；3—1.95；4—2.05。

通过上述分析可知：孔隙比、砂土颗粒弹性模量、埋深和颗粒形状修正系数对砂土剪切波速的影响显著，这也从一方面说明引入颗粒形状修正系数的合理性与必要性；有效内摩擦角、砂土颗粒泊松比和砂土密度对剪切波速影响很小；与配位数有关的常数对剪切波速影响较小。

4 算例

刘瑜[18]给出了浙江省多个工程勘察中测得的砂土剪切波速。结合实际工程地质条件，利用式(18)计算实际工程剪切波速，并与实测值进行比较。

由于砂土有效内摩擦角、砂土颗粒泊松比、砂土密度以及与配位数有关的常数对剪切波速影响较小，因此可取浙江省常见砂土数据。取有效内摩擦角，砂土颗粒泊松比，砂土密度= 2 000 kg/m3，与配位数有关的常数m=13，无附加荷载。由表1可见：实测土层深度较大，可认为砂土处于密实状态，取孔隙比=0.67。

对于砂土颗粒弹性模量以及颗粒形状修正系数，目前研究成果较少。夏唐代等[19]参考石英、水泥、磨细矿渣及粉煤灰颗粒的纳米压痕试验结果，提出可将砂土颗粒弹性模量取为10 GPa。本文取e=10 GPa。参考周志军等[12, 14, 20]对类似表面形状参数的研究，取颗粒形状修正系数=0.8。计算结果如表2所示。

表2 本文计算结果与实测值对比

Table 2 Comparison between calculated results and measured data

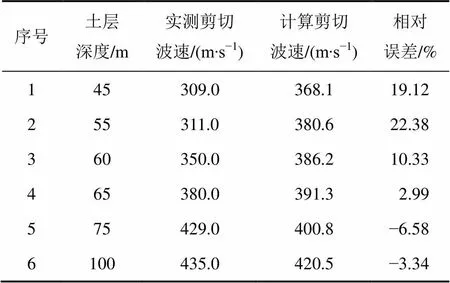
由表2可知：土层深度小于60 m时，本文计算值与实测值的相对误差为10%~20%，土层深度大于60 m时，本文计算值与实测值的相对误差在土5%以内。计算值与实测值变化趋势相同，能够反映剪切波速随土层深度增加而增加的趋势，在土层深度小于60 m时，计算值大于实测值，偏差不大，在土层深度大于60 m时，计算值与实测值偏差很小。总体来看，计算值能够有效地反映实测值，达到较好的准确度，从而说明从微观尺度引入颗粒形状修正系数研究砂土剪切波速的合理性。

对当土层深度较浅时计算值与实测值偏差稍大的情况，本文认为与计算时颗粒形状修正系数的选取有关。由于没有相应的数据，本文是结合文献进行合理估算，从结果上看，对于较深的土层，选取的颗粒形状修正系数较准确。但是对于埋深较浅处的土层，由于所处深度有效应力较小，所经历的地质作用较少，颗粒之间相互碰撞磨损较少，因此颗粒之间的粒径、形状差异更大，颗粒形状更加不圆顺，较之更深处土层颗粒，颗粒形状修正系数应更小，再结合图4可知：埋深较浅处上述计算剪切波速偏大，与表2所示情况相符。这反映了颗粒形状修正系数对砂土剪切波速影响的显著性，同时反映了颗粒形状修正系数的重要性，说明引入颗粒形状修正系数计算砂土剪切波速的合理性与必要性。

5 结论

1) 基于微观颗粒接触理论，结合散粒体微观组构与本构关系以及等径球体接触等研究，引入颗粒形状修正系数，宏观上将砂土视为连续介质，推导出砂土剪切模量与剪切波速的关系式，微观上将砂土假设为由等效球体半径相等、材料性质相同、随机堆积的固体颗粒组成的集合体，推导出了砂土剪切模量和砂土剪切波速计算公式。

2) 有效内摩擦角、砂土颗粒泊松比、砂土密度和与配位数有关的常数对剪切波速影响较小；孔隙比、砂土颗粒弹性模量、埋深和颗粒形状修正系数对砂土剪切波速的影响显著。对砂土颗粒弹性模量与颗粒形状修正系数的实验研究较少，目前缺乏更直观和准确的数据，有必要对两者进行系统的理论和实验研究。

3) 应用本文方法对砂土进行剪切波速计算，并与实测值进行比较。比较结果显示计算值与实测值拟合较好，同时反映了颗粒形状修正系数对砂土剪切波速的显著影响，说明本文方法的合理性。

[1] 周燕国. 土结构性的剪切波速表征及对动力特性的影响[D]. 杭州: 浙江大学建筑工程学院, 2007: 3−5. ZHOU Yanguo. Shear wave velocity-based characterization of soil structure and its effects on dynamic behavior[D]. Hangzhou: Zhejiang University. College of Architectural and Civil Engineering, 2007: 3−5.

[2] KAYEN R, MOSS R E S, THOMPSON E M, et al. Shear-wave velocity-based probabilistic and deterministic assessment of seismic soil liquefaction potential[J]. American Society of Civil Engineers, 2014, 139(3): 407−419.

[3] AHMADI M M, AKBARI−PAYDAR N. Requirements for soil-specific correlation between shear wave velocity and liquefaction resistance of sands[J]. Soil Dynamics and Earthquake Engineering, 2014, 57: 152−163.

[4] 孔梦云, 陈兴国, 李小军, 等. 以剪切波速与地表峰值加速度为依据的地震液化确定性及概率判别法[J]. 岩土力学, 2015, 36(5): 1239−1252. KONG Mengyun, CHEN Guoxing, LI Xiaojun, et al. Shear wave velocity and peak ground acceleration based deterministic and probabilistic assessment of seismic soil liquefaction potential[J]. Rock and Soil Mechanics, 2015, 36(5): 1239−1252.

[5] SAHAY P N. Biot constitutive relation and porosity perturbation equation[J]. Geophysics, 2013, 78(5): 57−67.

[6] BRANDT H, HABRA L. A study of the speed of sound in porous granular media[J]. Journal of Applied Mechanics, 1955, 22: 479−486.

[7] MAEDA K, SAKAI H, KONDO A, et al. Stress-chain based micromechanics of sand with grain shape effect[J]. Granular Matter, 2010(12): 499−505.

[8] SENETAKIS K, COOP M R, TODISCO M C. Tangential load-deflection behavior at the contacts of soil particles[J]. Geotechnique Letters, 2013(3): 59−66.

[9] CHUNG C K, JANG E R, BAEK S H, et al. How contact stiffness and density determine stress-dependent elastic moduli: a micromechanics approach[J]. Granular Matter, 2014, 16(1): 23−39.

[10] 李洪涛. 基于细观力学的颗粒材料宏观本构模型[D]. 大连: 大连理工大学工程力学系, 2010: 52−55. LI Hongtao. Macroscopic constitutive model of granular materials based on microscopic mechanics[D]. Dalian: Dalian University of Technology. Department of Engineering Mechanics, 2010: 52−55.

[11] 赵明阶, 吕卫兵. 多相土−石复合介质波动传播特性[J]. 岩石力学与工程学报, 2005, 24(增1): 4917−4923. ZHAO Mingjie, LÜ Weibing. Properties of wave propagation in polyphase soil−stone composite medium[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(Suppl 1): 4917−4923.

[12] 周志军, 朱宏祥, 张熠. 土石混合料结构强度的微观分析[J]. 中国公路学报, 2008, 21(3): 30−34. ZHOU Zhijun, ZHU Hongxiang, ZHANG Yi. Micro-analysis of structural strength of earth-rock mixture[J]. China Journal of Highway and Transport, 2008, 21(3): 30−34.

[13] 周志军, 刘海鹏, 赵小兵. 风积沙散体材料的本构关系[J]. 兰州理工大学学报, 2008, 34(1): 106−108. ZHOU Zhijun, LIU Haipeng, ZHAO Xiaobing. Constitutive relationship of dispersive material of wind-borne sand[J]. Journal of Lanzhou University of Technology, 2008, 34(1): 106−108.

[14] 王平, 万复光. 碎石道床的组构描述[J]. 西南交通大学学报, 1997, 32(2): 165−169. WANG Ping, WAN Fuguang. A description of microstructures of ballast bed[J]. Journal of Southwest Jiaotong University, 1997, 32(2): 165−169.

[15] 何思明, 罗渝, 吴永. 基于损伤理论的颗粒材料接触摩擦特性研究[J]. 四川大学学报(工程科学版), 2011, 43(1): 231−235. HE Siming, LUO Yu, WU Yong. Research on contact friction characteristic of particle material based on damage theory[J]. Journal of Sichuan University (Engineering Science Edition), 2011, 43(1): 231−235.

[16] MINDLIN R D. Compliance of elastic bodies in contact[J]. Journal of Applied Mechanics, 1949, 71: 259−268.

[17] DIGBY P J. The effective elastic moduli of porous granular rocks[J]. Journal of Applied Mechanics, 1981, 48: 803−808.

[18] 刘瑜.基于颗粒接触模型的砂土剪切波速研究[D]. 杭州: 浙江大学建筑工程学院, 2010: 49−52. LIU Yu. Research on sand shear wave velocity based on particle contact model[D]. Hangzhou: Zhejiang University. College of Architectural and Civil Engineering, 2010: 49−52.

[19] 夏唐代, 刘瑜, 吴明, 等. 基于颗粒接触理论的深层砂土剪切波速度[J]. 哈尔滨工业大学学报, 2011, 43(4): 99−103. XIA Tangdai, LIU Yu, WU Ming, et al. Shear wave velocity in deep buried sand based on spheres-contact theory[J]. Journal of Harbin Institute of Technology, 2011, 43(4): 99−103.

[20] 刘瑜, 夏唐代. 砂土颗粒粗糙度对剪切波速影响的试验研究[J]. 岩土工程学报, 2011, 33(2): 285−290. LIU Yu, XIA Tangdai. Experimental study on influence of particle roughness on shear wave velocity of sand[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(2): 285−290.

(编辑 赵俊)

Shear wave velocity in sand based on microscopic size

HUANG Bo1, 2, XIA Tangdai1, 2, ZHOU Xinmin3, LIU Zhijun1, 2

(1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;2. MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering, Zhejiang University, Hangzhou 310058, China;3. Seismological Bureau of Zhejiang Province, Hangzhou 310013, China)

Based on the macroscopic equivalent model and microscopic contact theories, the shear wave velocity was studied. Considered as a kind of homogeneous, continuous and isotropic media macroscopically, the sand was assumed microscopically as an aggregate of randomly packed uniform equivalent spheres with the same material properties. Then, the formulas of the equivalent shear modulus and shear wave velocity in sand were derived by using particle contact theory and by introducing the correcting coefficient of the granule shape. The main influencing factors were analyzed through quantitative calculations. The results indicate that the shear wave velocity is mainly influenced by void ratio, elastic modulus of sand granule, burial depth and the correcting coefficient of the granule shape, while it is hardly influenced by inner friction angle, Poisson’s ratio of sand granule, density of the sand and the constant connected with the coordination number. Through comparison, the calculation results using the present formulas agree well with measured data so as to verify the validity of the proposed method.

particle contact; correcting coefficient of the granule shape; equivalent sphere; equivalent shear modulus

10.11817/j.issn.1672-7207.2016.06.025

TU435

A

1672−7207(2016)06−2001−06

2015−06−10；

2015−09−20

国家自然科学基金资助项目(51378463，U1234204)(Projects(51378463, U1234204) supported by the National Natural Science Foundation of China)

夏唐代，博士，教授，博士生导师，从事土动力学及软土工程研究；E-mail：xtd@zju.edu.cn