改进的混合免疫算法在约束函数优化中的应用
2016-10-14张弛贾丽媛王加阳
张弛,贾丽媛,王加阳
改进的混合免疫算法在约束函数优化中的应用
张弛1, 2,贾丽媛2,王加阳1
(1. 中南大学信息科学与工程学院,湖南长沙,410083;2. 湖南城市学院信息科学与工程学院,湖南益阳,413000)
根据免疫算法多样性保持能力不足、易陷入局部最优等缺点,提出一种改进的混合免疫算法(improved hybrid immune algorithm,IHIA),将其与函数相结合,用于解决约束函数优化问题。采用个体字符串编码,通过信息熵法计算抗体亲和度,进而得到浓度。在混合免疫算法中提出克隆选择算子、可变阈值选择算子、郭涛精英变异和自适应变异概率算子等。研究结果表明:该算法提高了种群多样性和收敛性,减少了时间复杂度,提高了计算效率。
亲和力;信息熵;郭涛算法;自适应变异;约束函数
计算机科学与技术的迅速发展从根本上改变了人类的生产与生活,人们在获得极大方便的同时不得不面对规模越来越大的工程优化问题。这些优化问题的复杂度越来越高,很多问题都属于无确定解析式(non-deterministic polynomial,NP)。这些优化问题可以通过数学建模转化为函数优化问题,因而对函数优化问题的研究具有十分重要的意义。传统的优化算法有线性规划、动态规划、拟牛顿方法等,这些方法由于容易误入局部最优解,难以满足复杂问题的优化求解要求。免疫系统具有分布性、自适应性、群体多样性、自组织及快速应答的记忆特性等特点,模拟其功能而开发的人工免疫计算系统能解决大量的非线性问题[1−2]。用免疫算法解决工程问题也引起了广大计算智能学者的极大关注。自然免疫系统所使用的学习自适应机制能够连续产生负责检测和破坏外部分子的新抗体种类,而抗体多样性是其病原体识别能力的关键。人工免疫算法(AIA)[3−4]模拟了自然免疫系统基于浓度的抗体繁殖策略,对浓度较大的解进行抑制,从而有效地保持了解群的多样性,防止了成熟前收敛。这种多样性保持机制与遗传算法(GA)[5−6]的多样性保持机制虽有相似之处,但其本质是不同的。基于免疫系统多样性原理产生多样的候选个体解,对于优化等问题有望得到1个全局解。实践表明,AIA[7−8]的解的多样性保持策略实现简单,但它的运行速度慢,求解精度也有待提高。本文作者以函数优化为背景,提出一种改进的混合免疫算法(an improved hybrid immune algorithm,IHIA),从标准的免疫算法入手对其进行改进,以便在保持与AIA相近的多样性和收敛性的同时,达到减少算法提时间复杂度、提高求解精度的目的。
1 改进的混合免疫算法(IHIA)
1.1 免疫算法
免疫算法[9](immune algorithm,IA)是依据人体免疫学建立的一种新的生物智能算法,它模拟生物免疫系统中有关抗原处理的核心思想,包括抗体的产生、自体、克隆扩增,免疫记忆等。用免疫算法解决具体问题时,主要有以下定义。
1.1.1 亲和度计算
定义1 假设有个抗体,毎个抗体有个基因位,毎个基因位有个符号可供选择,即1,2,3,…,k,则这个抗体的信息熵(information entropy)为
定义2 (抗体的亲和度)用于表明两抗体之间的相似度。
第号抗体和第号抗体之间的亲和度定义为
式中:(2)为第号抗体和第号抗体的信息熵,(2)等于0时说明第号抗体和第号抗体所有基因都相同。a介于0和1之间。同样,抗体和抗原之间的亲和度定义为。其中,d为抗体与抗原之间的关异程度,采用解空间距离度量;a介于0和1之间。当d=0时,a=1,说明抗体和抗原非常匹配,即这个抗体是最优解。
1.1.2 抗体的浓度
定义3 抗体的浓度用于表示某个抗体以及与其很相似的抗体群的规模。第号抗体的浓度为
式中

1.1.3 一般免疫算法的主要步骤
1) 定义抗原。将需要解决的问题抽象成符合免疫系统处理的抗原形式,抗原识别则对应为问题的解。
2) 定义初始抗体群体。将抗体的群体定义为问题的解,抗体与抗原之间的亲和力对应问题的评估:亲和力越高,说明解越好。
3) 计算亲和力,即计算抗原与抗体之间的亲和力。
4) 克隆选择。与抗原有较大亲和力的抗体先得到繁殖,抑制浓度过高的抗体,淘汰低亲和力的抗体。为获得多样性(追求最佳解),抗体在克隆时经历变异。在克隆选择中,抗体促进和克隆删除对应优化解的促进与非优化解的删除等。
5) 评估新的抗体群体。若不能满足终止条件,则转向第3)步,重新开始;若满足终止条件,则当前的抗体为问题的最佳解。
1.2 改进的混合免疫算法(IHIA)
1.2.1 字符串编码
在本文中采用字符串编码实现。抗体和抗原由字符串编码方式,抗体亲和度由信息熵法计算。信息熵法不但可以对抗体的抗原亲和度进行度量,而且可以用于抗体多样性的度量。
1.2.2 克隆选择算子
抗体克隆选择算子是通过对抗体亲和度和抗体浓度综合考虑后而得到最终的抗体质量评价结果。一般是亲和度越大、浓度越低的抗体,克隆选择概率越大,其数学表达式为
其中:exc()为第个抗体的期望选择概率;()为抗体的亲和度;()为抗体的浓度;和分别为亲和度启发因子和浓度启发因子。
1.2.3 可变阈值选择算子
免疫选择算子可以依据抗体的期望选择概率来确定哪些抗体可以进入克隆选择操作。在通常情况下,期望选择概率的抗体会被选中进行克隆选择操作。
式中:()为第个个体的实际选择概率;为选择阈值[10],标准的免疫算法中固定不变。在本文的IHIA算法中,为加快算法的收敛速度,进行自适应动态调整:在算法进化初期阈值值设置较小,此时亲和度大和抗体浓度小的个体被选择克隆的机会大大增加;当算法进化到全局收剑时阈值设置较大,此时,亲和度大和抗体浓度小的个体被选择克隆的机会大大减少,提高了算法的速度。阈值调整策略如下:
式中:为阈值选择系数,取值为0.3;为当前进化代数;ave为进化代数平均值;max为最大进代数。
1.2.4 郭涛精英变异算子和自适应变异概率p
变异算子是对从克隆算子中得到的克隆抗体进行变异操作,以产生抗体在亲和度上的突变来实现局部搜索。它的作用是使免疫算法中突变生成有具较大潜力的新抗体,从而实现局部区域搜索功能的重要算子。为增加选择压力,加快算法的收敛速度,提出精英父代郭涛[11]变异算子。
郭涛精英变异算子是采用父代中按适应度高的个体(个)进行多父体精英子空间重组策略,它在精英子空间中搜索呈现非凸性:
1.2.5 局部收敛混沌优化算子
混沌[12]是自然界中普遍存在的一种非线性现象,其行为复杂,类似随机,存在精制的内在规律性。当算法陷入局部最优时,引入混沌优化算子:将记忆库中的记忆抗体进行混沌变异,以增加群体的多样性,扰动后的群体经过若干次迭代后达到全局最优状态。本文以典型的混沌系统Logistic映射进行相应的扰动操作。Logistic映射方程如下:
当3.56≤≤4.00时,Logistic映射在混沌状态。当嵌入混沌序列对群体进行扰动后,算法有较强的全局搜索能力,避免算法陷入局部最优,同时收敛速度也得到提高。
1.3 IAHA算法实现
步骤1 初始化种群。由记忆单元和保留种群P组成,即=P。初始时P随机生成,=0。中抗体的数目(组成记忆库)为种群总个数的30%。
步骤2 对种群解中的每个个体进行评价,即计算抗体的亲和度和浓度。从种群中选出个亲和力最高的抗体进入记忆库。
步骤3 克隆扩增操作。为保证亲和度越大、浓度越低的抗体克隆选择概率越大,抗体克隆操作按式(4)~(6)进行。其中每个个体克隆规模与亲和度成正比,即(其中:为克隆个体规模,f为个体的亲和度,为克隆控制系数)。
步骤4 变异操作。对克隆抗体进行郭涛精英变异,变异算子按式(7)进行。保证算法在进化初期亲和度大的抗体,采用较大的变异尺度以保持种群的多样性,而在进化后期亲和度小的抗体,采用较少尺度的变异,以提高局部微调能力。变异概率p采用自适应策略,按式(8)进行。
步骤5 记忆库更新。从已变异后的克隆抗体中重新选择亲和度高的个个体组成记忆库,同时,将父代个体中亲和度低的个体淘汰,重新生成下一代种群。
步骤6 局部收敛混沌优化。判断算法是否陷入局部收敛,若算法已陷入局部收敛,则记忆库抗体(占记忆库总数40%)执行局部收敛混沌优化操作,按式(11)进行。否则转步骤2。
步骤7 以进化代数max作为终止条件,判断是否满足结束条件。若满足结束条件,则终止程序,输出解;否则,转步骤2。
2 仿真实验与结果分析
2.1 实验参数分析与设置
1)抗体种群大小。抗体种群大小一般取50~150。对于峰值较密的多峰值函数,为了找出尽量多的极值点,群体规模取大些,本文取200。
2)亲和度越大,则浓度越低的抗体克隆选择概率越大。本文亲和度启发因子取3,浓度启发因子取4。
3) 克隆数。克隆数对算法的收敛速度影响较大。克隆数越大,算法进化速度越快,抗体移动到极值点所需代数变越少,但算法的时间复杂度会增加。为了在收敛速度和时间复杂度之间进行权衡,经过仿真实验,本文克隆控制系数取25。
4) 亲和度值。这里将抗体解码后所对应的函数值作为抗体的亲和度。
5)终止条件。最大循环次数max(次数)=800。
2.2 仿真结果与分析
为了测试本文算法,采用13个标准测试问题[15−16]中6个有代表性的标准测试函数进行仿真,并与文献[15]和[16]中的算法进行对比实验。文献[15]和[16]中的算法运行参数均按照相应文献中的最优化设置。在上述情况下,给出4种算法在6个检测函数上20次独立实验的最优值(best)、最差值(worst)、平均值(mean)、最优解的最短时间()、最优解的次数(nbest)和平均百分误差(,其中,为第次的最优路径,0为已知最优值),如表1所示。
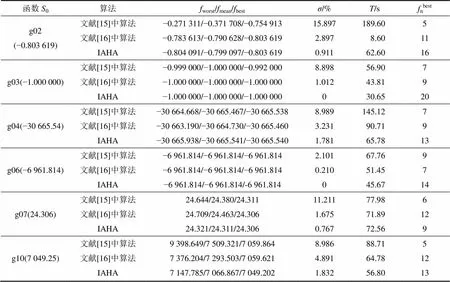
表1 采用不同算法所得6个标准测试函数的实验结果
从表1可看出:对于检测函数除g10外,本文算法IAHA均获得最优结果best;对于检测函数g10,IHIA算法虽然没有得到最优值,但所得结果与最优值的误差很小;对于平均百分误差,本文算法IAHA都比其他2种算法的小;检测函数g03和g06平均百分误差都为0,这说明IAHA算法求解精度较高;从最优解的最短时间来看,除检测函数g07外,本文算法IAHA获得最优解的时间最少,说明IAHA算法收全局收敛速度快;在对检测函数都运行20次且参数相同条件下,除检测函数g07外,其他检测函数最优解的次数(nbest)最多,g02,g04,g06和g10分别达到16,13,14和13次,其中g03检测函数nbest达到20次,说明本文的IAHA算法有很强的鲁棒性。可见IAHA是一种求解约束优化问题的有效算法。图1和图2所示分别为本文算法IAHA和文献[13]和[14]中算法求解进化曲线和最优解耗时曲线。
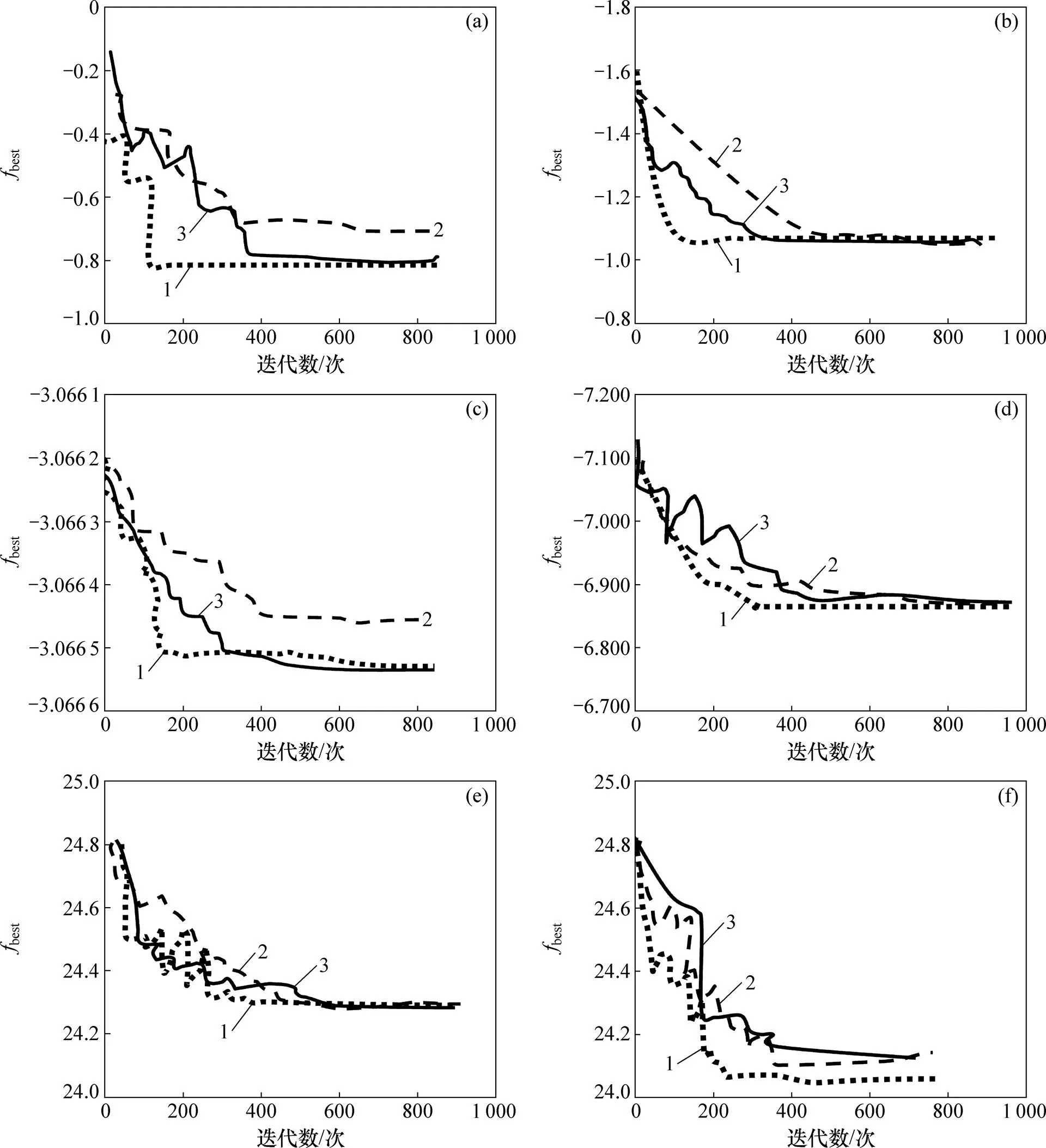
函数:(a) g02;(b) g03;(c) g04;(d) g06;(e) g07;(f) g10 1—IAHA算法;2—文献[13]中算法;3—文献[14]中算法。
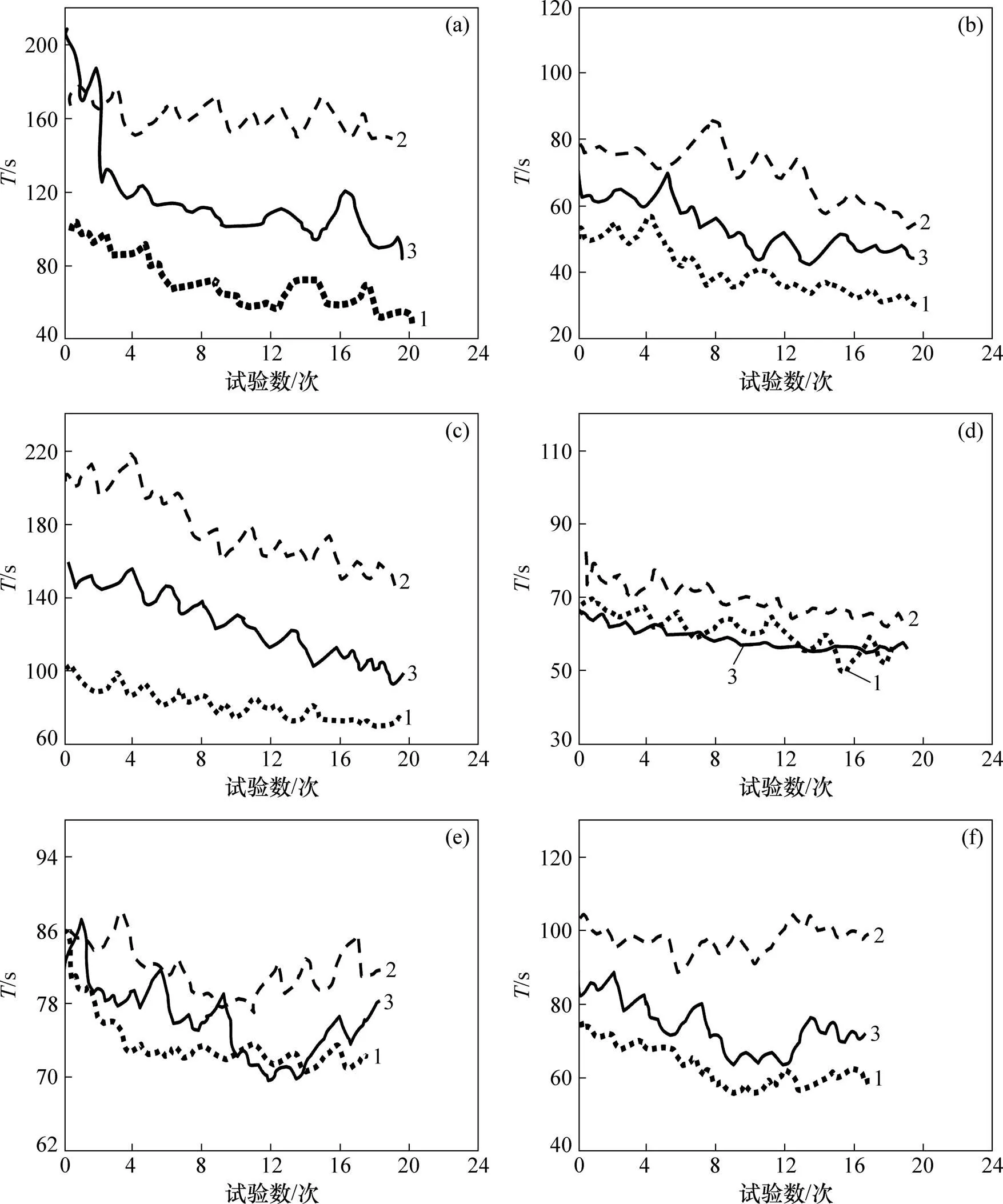
函数:(a) g02;(b) g03;(c) g04;(d) g06;(e) g07;(f) g10 1—IAHA算法;2—文献[13]中算法;3—文献[14]中算法。
从图1可以看出:在3种算法中,除检测函数g07外,本文算法IAHA求解稳定性比文献[13]和[14]中的算法都强;同时IAHA算法在所有的检测函数中都表现出搜索速度快的特点。对于g02,g03和g04,一方面,IAHA算法在迭代代数200代之前都已经达到全局最优;另一方面,IAHA算法的全局最优解都比文献[13−14]中的算法优。对于检测函数g02,文献[13]中的算法在第370代获得最优解−0.701 287,文献[14]中的算法在第390代获得最优解−0.802 845,本文IAHA算法在第180代获得最优解−0.803 612,此解接近于理解最优解−0.803 619。对于检测函数g04,文献[13]中算法在第410代获得最优解−30 664.990,文献[14]中算法在第400代获得最优解−30 665.238,本文IAHA算法在第189代获得最优解−30 665.530,此解接近于理论最优解−30 665.54。对于检测函数g06,文献[13]中算法在第408代获得最优解−6 905.675,文献[14]中算法在第458代获得最优解−6 961.814,本文IAHA算法在第359代获得最优解−6 961.814,此解为理论最优解−6 961.814。对于检测函数g07,本文IAHA算法前期搜索阶段表现不是很稳定,最优解有波动现象,但在中后期的表现要比文献[13]和[14]中的算法好。文献[13]中算法在第40代获得最优解24.350,文献[14]中算法在第458代获得最优解24.310,本文IAHA算法在第280代获得最优解24.308,此解接近于理论最优解24.306。对于检测函数g10,文献[13]中算法在第400代获得最优解7 156.897,文献[14]中算法在第410代获得最优解7 180.765,本文IAHA算法在第280代获得最优解7 059.650,此解接近于理论最优解7 049.25。
从图2可以看出:对于检测函数g02,g03,g04和g10的各20次实验,本文算法IAHA的寻优时间都少于文献[13]中算法和文献[14]中算法寻优时间,同时本文算法IAHA最优解的最短时间比文献[13]和[14]中算法的少。对于检测函数g06,本文算法IAHA的寻优时间都少于文献[13]中的算法时间,可平均寻优时间比文献[14]中的高。对于检测函数g07,除第13次和第15次实验本文算法IAHA寻优时间高于文献[14]中的外,其余寻优时间和平均寻优时间都比文献[13]和[14]中算法的寻优时间低。从表1、图1和图2可见算法IAHA是高效的。
3 结论
1) 针对约束函数优化问题提出一种改进的混合免疫算法(improved hybrid immune algorithm, IHIA)。该算法的特点在于:提出克隆选择算子,亲和度越大,浓度越低的抗体克隆选择概率越大,这样增加了个体的多样性;提出可变阈值选择算子,选择阈值自适应进行调整,提高了算法的寻优速度且避免了算法陷入局部最优;提出郭涛精英变异算子和自适应变异概率m,能加快局部搜索速度;局部收敛混沌优化算子,有利于算法跳出局部最优而达到全局最优。
2) 该算法求解约束优化问题,能进行稳定、快速地全局寻优。
[1] ZHANG Zhuhong. Immune optimization algorithm for constrained nonlinear multi-objective optimization problems[J]. Applied Soft Computing Journal, 2007, 7(3): 840−857.
[2] ZUO Xingquan, MO Hongwei, WU Jianping. A robust scheduling method based on a multi-objective immune algorithm[J]. Information Sciences, 2009, 179(19): 3559−3369.
[3] 郭一楠, 王辉, 程键. 自适应免疫克隆算选择文化算法[J]. 电子学报, 2010, 38(4): 966−970. GUO Yinan, WANG Hui, CHENG Jian. Adaptive immune clonal system cultural algorithm[J]. Acta Electronica Sinica, 2010, 38(4): 966−970.
[4] 张著洪, 钱淑渠. 自适应免疫算法及其对动态函数优化的跟踪[J]. 模式识别与人工智能, 2007, 20(1): 85−88.ZHANG Zhuhong, QIAN Shuqu. Adaptive immune algorithm and its track to dynamic function optimization[J]. Pattern Recognition and Artificial Intelligence, 2007, 20(1): 85−88.
[5] 王凌. 智能优化算法及应用[M]. 北京: 清华大学出版社, 2001: 1−76. WANG Liing. Intelligent optimization algorithm with applications[M]. Beijing: Tsinghua University Press, 2001: 1−76.
[6] 周明, 孙树栋. 遗传算法原理及应用[M]. 北京: 国防工业出版社, 1999: 5−9. ZHOU Ming, SUN Shudong. Genetic algorithm theory and applications[M]. Beijing: National Defence Industry Press, 1999: 5−9.
[7] 于帆, 李纪鑫. 免疫算法在近红外光谱奇异样本识别中的应用[J]. 西安工业大学学报, 2014, 34(1): 38−41. YU Fan, LI Jixin. Immune algorithm for identification of singular sample with near infrared spectroscopy[J]. Journal of Xi’an Technological University, 2014, 34(1): 38−41.
[8] 郑涛, 潘玉美. 基于免疫算法的配电网故障定位方法研究[J]. 电力系统保护与控制, 2014, 42(1): 56−60. ZHENG Tao, PAN Yumei. Research on electric distribution network fault location method based on immune algorithm[J]. Power System Protection and Control, 2014, 42(1): 56−60.
[9] 肖人彬, 王磊. 人工免疫系统: 原理, 模型, 分析及展望[J]. 计算机学报, 2002, 25(12): 1281−1290. XIAO Renbin, WANG Lei. Artificial immune system: principle, models, analysis and perspectives[J]. Chinese Journal of Computers, 2002, 25(12): 1281−1290.
[10] 翟宏群, 冯茂岩. 一种改进的变阈值阴性选择免疫算法[J]. 南京师范大学学报(工程技术版), 2011, 11(3): 78−82. ZHAI Hongqun, FENG Maoyan. An improved adjustable threshold intrusion detection negative selection immune algorithm[J]. Journal of Nanjing Normal University (Engineering and Technology Edition), 2011, 11(3): 78−82.
[11] GUO Tao, MICHALEWICZ Z. Inver-over operator for the TSP[C]//Proceedings of the 5th International Conference on Parallel Problems Solving from Nature. Lecture Notes in Computer Science, Berlin: Springer, 1998: 803−812.
[12] 毛永毅, 王瑶. 基于双混沌系统互反馈的加密算法[J]. 计算机应用, 2012, 32(10): 2768−2770, 2775. MAO Yongyi, WANG Yao. Encryption algorithm based on double chaos system with mutual feedback[J]. Journal of Computer Applications, 2012, 32(10): 2768−2770, 2775.
[13] 尚荣华, 焦李成, 马文萍. 免疫克隆多目标算法求解约束优化问题[J]. 软件学报, 2008, 19(11): 2943−2956. SHANG Ronghua, JIAO Licheng, MA Wengping. Immune clonal multi-objective optimization algorithm for constrained optimization[J]. Journal of Software, 2008, 19(11): 2943−2956.
[14] 杨剑, 张敏辉. 求解约束优化问题的改进型免疫算法[J]. 计算机应用研究, 2011, 28(11): 4029−4031. YANG Jian, ZHANG Minhui. Novel immune algorithm for solving constrained optimization problems[J]. Application Research of Computers, 2011, 28(11): 4029−4031.
(编辑 陈灿华)
An improved hybrid immune algorithm for multimodal optimization
ZHANG Chi1, 2, JIA Liyuan2, WANG Jiayang1
(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;2. School of Information Science and Engineering, Hunan City University, Yiyang 413000, China)
To improve the efficiency of basic artificial immune algorithm(AIA), an improved hybrid immune algorithmn (IHIA) was presented for constrained optimization. To maintain high diversity, the fitness of each individual and concerntration were taken into accounted to determine reproduction probability. Many benchmark functions were used to demonstrate the validity and the role of each design of IHIA. The results show that IHIA can reduce the complexity of computation, and increase the efficiency with the maintenance of diversity and convergence in optimizing costrained functions.
affinity; information entropy; Guotao algorithm; adaptive mutation; constrained function
10.11817/j.issn.1672-7207.2016.06.016
TP18
A
1672−7207(2016)06−1940−07
2015−07−10;
2015−09−21
湖南省教育科学“十二五”规划课题(XJK014CGD013);益阳市科技计划项目(2014JZ52)(Project(XJK014CGD013) supported by “Twelfth Five-year” Planning Program of Hunan Education Science; Project(2014JZ52) supported by Science and Technology Planning Project of Yiyang City)
张弛,硕士,讲师,从事计算机图像处理和算法研究;E-mail:carol_zc@126.com
