带落角和时间约束的网络化导弹协同制导律

张春妍，宋建梅，侯博，张民强

（北京理工大学宇航学院，北京100081）

带落角和时间约束的网络化导弹协同制导律

张春妍，宋建梅，侯博，张民强

（北京理工大学宇航学院，北京100081）

对网络化导弹的协同攻击问题进行了带命中落角约束和攻击时间约束的协同偏置比例导引律研究。对单枚导弹给出了带命中落角约束的偏置比例导引律，并推导出了对应的导弹剩余攻击时间的估算表达式。针对网络化导弹系统，根据各导弹的剩余攻击时间之差对偏置比例导引律中的比例系数进行调节，设计得到了同时满足命中落角和攻击时间约束的协同偏置比例导引律，进一步从理论上证明了该导引律能够使多枚导弹的攻击时间趋于一致。网络化导弹制导系统数学仿真实验结果表明，协同偏置比例导引律及剩余攻击时间估算方法是有效和正确的。

控制科学与技术；协同制导律；命中落角约束；攻击时间约束；剩余攻击时间

0 引言

多导弹协同将是未来战场的一种重要作战方式，多枚导弹借助通信系统构成一个作战网络，通过信息共享提高武器系统的突防攻击、目标精确识别和电子对抗等能力，增强打击毁伤效果［1-2］。对大型军舰、弹道导弹运输车、加固的地下工事等具有重大军事价值的目标，若网络化导弹能够同时精确命中目标或者目标的关键部位，还能以不同的期望落角命中目标，则将最大限度地发挥各导弹战斗部效能［3］，对目标形成毁灭性打击。基于此，本文研究同时带命中落角和攻击时间约束的网络化导弹协同制导律，使网络化导弹能以不同的期望落角在同一时刻精确命中目标的不同关键部位，充分发挥网络化导弹系统的精确打击能力。

关于只带命中落角约束的制导律研究成果已有很多，如偏置比例导引律［4-7］、最优制导律［8-10］、局部综合制导律［11］等。早在1998年，Kim等［6］就提出了一种偏置的比例导引律，并对脱靶量和末端弹道倾角的收敛性给出了详细的理论证明。高峰等［5］和Lee等［7］均在假设偏置项为常数的条件下，推导出了带命中落角约束的偏置比例导引律。文献［7-8］基于最优控制理论，以终端时刻弹道倾角与期望落角之差、脱靶量以及法向加速度指令之和为目标函数，求解出了最优制导律，其形式与文献［5］中所推导的偏置比例导引律形式一致，说明偏置比例导引律能够使导弹脱靶量和加速度过载指令最小，终端时刻弹道倾角达到期望落角。

对于只带攻击时间约束的制导律，目前的研究成果分为两类：一类是，将针对单枚导弹研究的能够实现预期打击时间的制导律推广应用于网络化导弹系统［12-14］，在这种情况下，各导弹之间没有信息交换，没有实现真正意义上的协同作战，且设定的期望打击时间通常比较长；另一类是，各导弹在飞行过程中进行实时信息交互，通过获取其余导弹的剩余攻击时间来调整自身的飞行时间。文献［15］将剩余攻击时间之差作为比例导引系数的参变量，设计了含有时变比例系数的协同比例导引律来控制弹道弯曲程度，通过调整飞行长度使得所有导弹的剩余攻击时间一致。文献［16］采用领弹-从弹策略，选取初始剩余攻击时间最长的弹为领弹，其余为从弹，在俯仰通道采用增广比例导引使所有导弹的速度矢量前置角趋于0°，再基于动态逆方法形成机动控制指令，使从弹与领弹的剩余攻击时间一致。文献［17］也采用领弹-从弹策略，领弹采用比例导引，从弹以领弹攻击时间为参量设计附加的法向过载，再叠加比例导引，使得从弹的弹目相对距离和速度矢量前置角与领弹的一致，以达到同时打击的目的。文献［18］设计了含有上层协调控制和底层导引控制的双层协同制导结构，上层协调控制单元根据协调策略给出协调变量，再由各导弹接收协调变量实现底层导引律，此协同制导结构为导弹协同制导问题提供了一定的通用性解决方案。

目前对同时带命中落角和攻击时间约束的制导律研究相对较少。文献［19］针对单枚导弹提出了一种带落角约束的偏置比例导引律，并推导了较精确的剩余攻击时间计算公式，然后将剩余攻击时间与期望的攻击时间之差作为反馈项，加入到偏置比例导引律中，设计出了一种同时约束攻击时间和命中落角的制导律。文献［20］针对单枚导弹，以实时弹目视线角与期望落角之差作为滑动面，以期望攻击时间与预测攻击时间之差作为目标函数，基于2阶滑模控制和最优控制理论设计了带命中落角和攻击时间约束的制导律。文献［21］针对单枚导弹，首先推导了一种带命中落角约束的最优制导律，并推导出了相应的导弹剩余攻击时间表达式，然后将剩余攻击时间与期望攻击时间之差作为附加反馈信号加入到过载指令中，使得导弹能以期望的攻击时间命中目标，并达到期望落角。由于文献［19-21］均针对单枚导弹进行研究，所以不存在协同问题。文献［22］针对协同作战的网络导弹系统提出了一种可以控制命中角度和攻击时间的协同制导方法。文中首先选取一枚导弹作为领弹，以目标位置为圆心，领弹与目标的相对距离为半径构造一个虚拟球体，根据从弹的期望落角确定从弹在虚拟球体上对应的虚拟点，然后基于最优控制理论设计状态调节器，控制从弹逼近并跟踪虚拟点，最终达到协同作战的目的。该文献采用领弹-从弹策略，需要事先确定领弹，且系统最终的攻击时间取决于领弹。而本文提出的制导律是一种分布式协同制导律，无需确定领弹，系统最终攻击时间由网络中各导弹的剩余攻击时间综合而成，作战时间相对较短，在实际应用中更为方便有效。

本文进行了同时带命中落角和攻击时间约束的网络化导弹协同制导系统研究，创新点主要有两点：1）基于导弹飞行弹道的长度，推导了带命中落角约束的偏置比例导引律作用下的导弹剩余攻击时间估计表达式，考虑了用于落角控制的过载指令对弹道曲率的影响，因而导弹剩余攻击时间的估算比较准确；2）提出了一种可同时约束命中落角和攻击时间的网络化导弹协同偏置比例导引律，并从理论上证明了该导引律能够使网络化导弹系统的剩余攻击时间方差收敛至0，可保证各导弹能够以不同期望落角同时命中目标或者目标的不同关键部位。

1 带命中落角约束的偏置比例导引律及剩余攻击时间估计

1.1带命中落角约束的偏置比例导引律

考虑图1所示的导弹与目标的相对运动关系，AXY为惯性坐标系，T为目标，假设目标静止，（xT，yT）为目标的位置；M为导弹，（x，y）为导弹的瞬时位置，v为导弹的切向速度，假设v为常值，an为导弹的法向加速度，σ为导弹的弹道角，规定速度矢量指向AX轴上方时σ为正，反之为负；R为弹目相对距离；q为弹目视线角，规定由水平基准线逆时针旋转到弹目视线上时q为正，反之为负；η为导弹速度矢量前置角，规定由导弹速度矢量逆时针旋转到弹目视线上时η为正，反之为负。

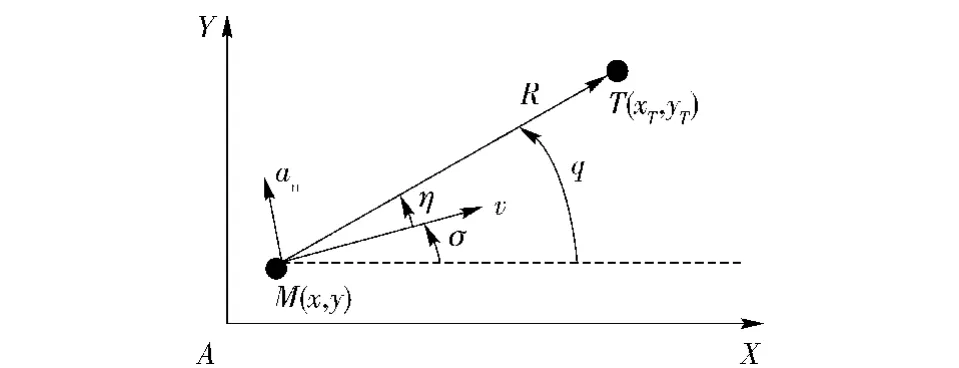
图1　导弹与目标的相对运动关系示意图Fig.1 Relative motion between missile and target

弹-目相对运动方程为

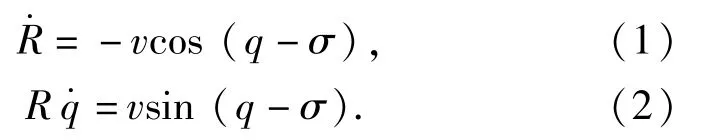
导弹的运动方程为

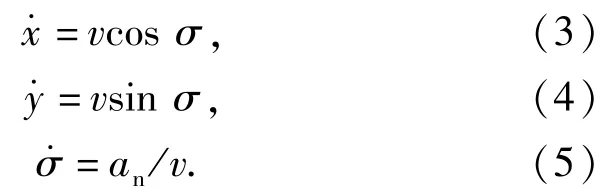
由于η=q-σ，则

为了使导弹能够以期望落角击中目标，采用在比例导引基础上加入偏置项的方法，其一般形式为

式中：N为比例系数；aB为偏置项。将（7）式代入（5）式，得

根据导数的定义，可知在某一小段时间Δt内，有

式中：下标t和t+Δt分别表示Δt时间段的初始时刻和末时刻。假设aB在每个Δt时间段内均为常数，则将Δt拓展为总飞行时间可得

式中：下标0和f分别表示整个飞行过程的初始时刻和末时刻。

当导弹击中目标时，R（tf）=0，根据（2）式可得

设σd为期望落角，令

即希望导弹终端时刻的弹道角能达到期望落角，则由（10）式整理可得

由于tf可以看作是导弹飞行初始时刻的剩余攻击时间，则偏置项aB用当前时刻的参数可表示为

式中：tgo表示导弹当前时刻的剩余攻击时间。

若tgo≈R/v，则带命中落角约束的偏置比例导引律为

在此导引律中，剩余攻击时间的估计没有考虑法向加速度指令对飞行弹道曲率和剩余飞行时间的影响。如果该导引律只是用于单枚导弹制导系统，且系统对攻击时间没有要求，则该导引律对导弹脱靶量和命中落角控制精度没有明显影响［5］。本文拟将此偏置比例导引律推广应用于网络化导弹的协同制导，协同制导系统要求各导弹攻击时间必须一致，因此制导系统对剩余飞行时间的估算精度要求较高。

本文拟先针对单枚导弹，推导在上述偏置比例导引律作用下导弹的较精确剩余攻击时间估算表达式，然后将其推广应用于多枚导弹的协同制导。

1.2带命中落角约束的偏置比例导引律作用下的导弹剩余攻击时间估算

在进行剩余攻击时间估算时，不仅要考虑比例导引过载指令对弹道曲率的影响，还要考虑用于落角控制的过载指令对弹道的影响。本文提出了一种带落角约束的偏置比例导引律作用下的导弹剩余攻击时间估算方法。其基本思想是，根据（15）式中设计的带落角约束的偏置比例导引律，近似拟合出导弹的飞行弹道，在假设速度恒定的情况下，根据飞行弹道总长度估算出导弹的剩余飞行时间，详细推导过程如下。

定义弹目视线坐标系OXLOSYLOS：坐标系原点O取在初始时刻导弹的瞬时质心处，OXLOS轴与初始时刻弹目视线重合，指向目标为正，OYLOS轴与OXLOS轴垂直，以图2所示方向为正。

弹目视线坐标系与惯性系的几何关系示意图如图2所示。图2中，σ0和q0分别为初始时刻的弹道角和弹目视线角。导弹与目标在弹目视线坐标系下的相对运动关系如图3所示。

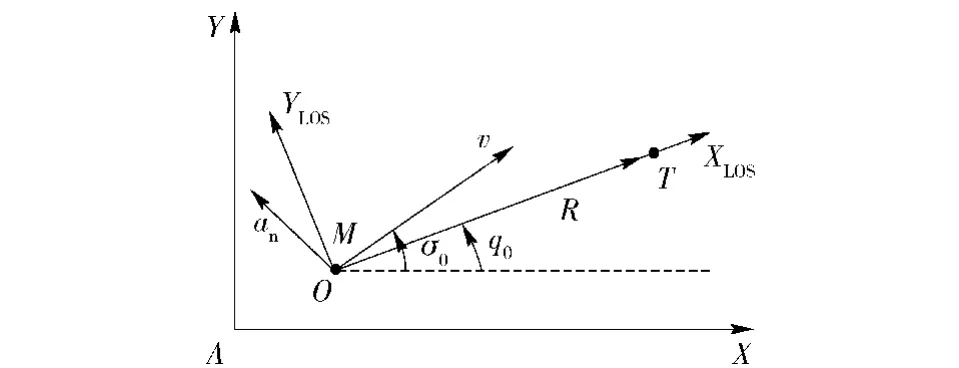
图2　弹目视线坐标系与惯性坐标系的几何关系示意图Fig.2 Line-of-sight frame and inertial frame

图3　弹目视线坐标系中的弹目相对运动关系示意图Fig.3 Relative motion between missile and target in line-of-sight frame

设图3中曲线为导弹的飞行弹道，弹目视线坐标系下目标位置为（xf，0）、导弹位置为（xs，ys）。令φ为导弹速度方向与OXLOS轴的夹角，规定导弹速度矢量指向OXLOS轴上方时φ为正，反之为负；λ为弹目视线与OXLOS轴的夹角，规定弹目视线方向指向OXLOS轴上方时λ为正，反之为负。

由几何关系可得

下文中规定上标“＇”代表各参数对xs的导数。假设φ和λ均为小角度，则ys和φ关于xs的导数为

弹目视线角可表示为

将（17）式和（18）式代入（15）式，可得法向加速度关于xs的表达式：

将（19）式代入（17）式，由于初始条件为ys（0）=0，y＇s（0）=φ0，解得ys关于xs的表达式为

φ关于xs的表达式为

导弹的总飞行长度可以表示为

式中：tf为导弹的总飞行时间。

将（21）式代入（22）式，整理可得

可将tf看作是导弹初始飞行时刻的剩余攻击时间，xf看作是初始时刻的弹目相对距离R，φ0与初始的速度矢量前置角η大小相等，方向相反，即则导弹当前时刻的剩余攻击时间tgo可表示为

当不考虑落角约束，仅采用比例导引，即aB=0时，可得

将（25）式代入（24）式，整理可得

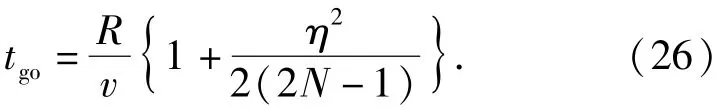
当仅采用比例导引而不考虑落角约束时，（26）式与文献［15］中推导的剩余攻击时间的表达式一致。

2 同时带命中落角和攻击时间约束的网络化导弹协同偏置比例制导律与剩余攻击时间方差收敛性证明

2.1同时带命中落角和攻击时间约束的网络化导弹协同偏置比例制导律

为了提高网络化导弹的作战效能，一般希望网络中的各导弹能够在同一时刻以不同的期望落角命中目标或者目标的不同关键部位，实现最佳毁伤，因此需要为网络化导弹设计同时带命中落角和攻击时间约束的协同制导系统。基于此，本文提出了一种协同偏置比例导引律。此导引律根据各枚导弹剩余攻击时间之差对比例导引系数进行调节，从而达到控制各导弹攻击时间一致并实现不同期望落角的目的。本文提出的协同偏置比例导引律的形式如下：

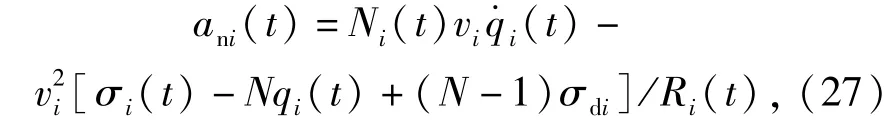
式中：下标i表示第i枚导弹；qi（t）为弹目视线角；为弹目视线角速率；σi（t）为导弹的弹道角；σdi为期望落角；Ni（t）为变比例系数，其表达式为Ni（t）=N（1-Ωi（t）），其中Ωi（t）为时变增益率，表达式为

其中

可将（27）式改写为如下形式：

式中：

ati（t）主要用于调节导弹的攻击时间，这里对攻击时间的调节转化为对弹道曲率和飞行距离的控制，即通过调节比例系数改变导弹飞行长度和弹道曲率，从而达到控制各导弹攻击时间一致的目的；aBi（t）则主要用于导弹的落角控制。由于在剩余时间估算表达式中明确考虑了比例导引过载指令和落角控制过载指令对飞行弹道曲率的影响，使得网络化导弹最终能够在同一时刻以各自期望的落角命中目标。下面从理论上对本文提出的协同偏置比例导引律的剩余攻击时间方差收敛性进行证明。

2.2协同偏置比例导引律的剩余攻击时间方差收敛性证明

网络化导弹系统的剩余攻击时间方差可表示为

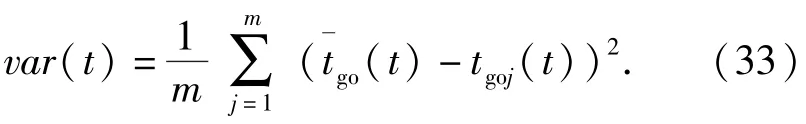
若协同制导律能够使（33）式中的方差收敛至0，则表明所有导弹的剩余攻击时间达到一致，即各导弹能够同时命中目标。下面将证明本文提出的协同偏置比例导引律能够使该方差收敛至0.

（29）式可写为

则（28）式可表示为

假设ηi（t）为小角度，则将各参数在t+Δt时刻的值在t时刻泰勒展开，并省去高阶小量，得

则根据（24）式，可得第i枚导弹在t+Δt时刻的剩余攻击时间为

则t+Δt时刻所有导弹的平均攻击时间为

将（35）式、（39）式和（40）式代入（33）式，则t+Δt时刻剩余攻击时间的方差可表示为

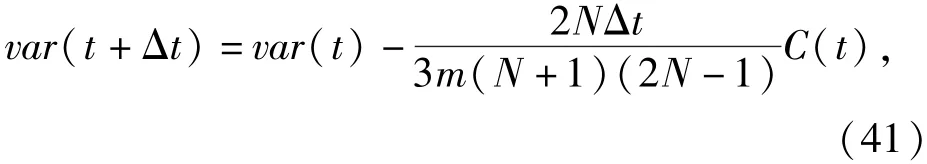
式中：

由（42）式可以看出，C（t）中的各项均为非负数，因此var（t+Δt）≤var（t），方差随着时间递减，并最终收敛至0，从而保证了多枚导弹能够同时命中目标。值得注意的是，当所有导弹在每个时刻均满足（3N-1）η（t）+（N-1）（σd-q（t））=0或η（t）=0时，var（t+Δt）=var（t），方差不会递减至0，而是维持一恒定值。但这种情况极其特殊，在实际作战中很难出现。

3 带命中落角和攻击时间约束的网络化导弹协同偏置比例导引律的仿真实验验证

3.1本文提出的协同偏置比例导引律的有效性验证

假设使用两枚导弹攻击同一目标，（xT，yT）= （8 000 m，0 m）；弹1初始位置坐标为（0 m，0 m），σ01=20°，σd1=-25°，v1=280 m/s；弹2初始位置坐标为（450 m，1 000 m），σ02=-5°，σd2=-35°，v2= 280 m/s.取N=3，K=40，运用本文提出的协同偏置比例导引律对两枚导弹进行协同制导仿真，得到两枚导弹的主要特征变量变化曲线如图4所示。

图4　两枚导弹协同攻击目标的仿真结果Fig.4 Cooperative attack of two missiles

由图4可以看出，弹1和弹2以各自期望的落角同时命中目标，验证了本文提出的网络化导弹协同制导律的正确性和有效性。最终弹1脱靶量为0.499 m，弹2脱靶量为0.498 m.由图4（d）可见，两枚弹的比例导引系数最终都收敛于3，这是由于两弹之间的剩余攻击时间之差随着导弹飞行逐渐趋于0，时变增益率也随着趋于0，因此比例系数收敛于给定的常系数N.

若采用（26）式进行各导弹剩余攻击时间的估算，即不考虑用于控制命中落角的过载指令对飞行时间的影响，则上述两枚导弹的协同制导效果如图5所示。

从图5可以看出，两枚导弹没有同时命中目标，剩余攻击时间方差最终没有收敛至0.研究表明，采用本文提出的协同偏置比例导引律对网络化导弹进行协同制导时，需采用本文提出的比较精确的剩余攻击时间估算方法，否则各导弹的攻击时间会存在一定的误差。

3.2多导弹协同攻击大型目标时的有效性验证

将目标的俯视图简化为六边形，假设使用3枚导弹在偏航平面内同时攻击目标3条边的中点，弹1初始位置坐标为（400 m，600 m），目标点位置为（8 550 m，75 m），σ01=-30°，σd1=30°，v1=300 m/s；弹2初始位置坐标为（0 m，500 m），目标点位置为（8500 m，0 m），σ02=0°，σd2=0°，v2=300 m/s；弹3初始位置坐标为（800 m，0 m），目标点位置为（8 550 m，-75 m），σ03=25°，σd3=-30°，v3=300 m/s.取N=3，K=30，运用本文提出的协同偏置比例导引律对3枚导弹进行制导仿真，各导弹的主要特征变量变化曲线如图6所示。

从图6可以看出，应用本文提出的带命中落角和攻击时间约束的协同偏置比例导引律，可以保证网络中各导弹在同一时刻以不同的期望落角命中目标的不同关键部位。最终弹1脱靶量为0.497 m，弹2脱靶量为0.499 m，弹3脱靶量为0.497 m.

图5　剩余攻击时间估算不准确情况下的导弹协同制导效果Fig.5 Cooperative attack of two missiles at inaccurate time-to-go

图6　3枚导弹攻击大型目标不同位置点时的仿真结果Fig.6 The different points of a large target attacked by three missiles

4 结论

本文对多导弹协同攻击问题进行了研究。首先针对单枚导弹给出了带命中落角约束的偏置比例导引律，然后综合考虑比例导引过载指令和落角控制过载指令对飞行弹道曲率的影响，提出了一种较为精确的导弹剩余攻击时间估算方法。将该导引律推广应用于网络化导弹，提出了一种带命中落角约束和攻击时间约束的协同偏置比例导引律。该导引律由两部分过载指令组成，一部分用来进行落角控制，另一部分用来调节导弹的攻击时间，即根据各导弹的剩余攻击时间之差，调节各导弹比例导引律中的比例系数以改变导弹的弹道曲率和飞行长度，最终达到控制各导弹攻击时间一致的目的。本文从理论上给出了该协同偏置比例导引律的收敛性证明。最后进行了网络化导弹协同制导系统数学仿真实验验证，并指出剩余攻击时间估算的准确性对攻击时间的一致性有一定影响。研究表明，本文提出的协同偏置比例导引律能够保证网络中各导弹以不同的期望落角同时命中目标或者目标的不同关键部位，能够满足未来战场上的多导弹协同作战需求。

（References）

［1］ 肖增博，雷虎民，滕江川，等.多导弹协同制导规律研究现状及展望［J］.航空兵器，2011（6）：18-22. XIAO Zeng-bo，LEI Hu-min，TENG Jiang-chuan，et al.The present status and prospect of multi-missile cooperative guidance law［J］.Aero Weaponry，2011（6）：18-22.（in Chinese）

［2］ 张克，刘永才，关世义.本系作战条件下飞航导弹突防与协同攻击问题研究［J］.战术导弹技术，2005（2）：1-7. ZHANG Ke，LIU Yong-cai，GUAN Shi-yi.An investigation into the issues of penetration and cooperative engagement for aerodynamic missile under the condition of systems coutermeasures［J］. Tactical Missile Technology，2005（2）：1-7.（in Chinese）

［3］ 蔡洪，胡正东，曹渊.具有终端角度约束的导引律综述［J］.宇航学报，2010，31（2）：315-323. CAI Hong，HU Zheng-dong，CAO Yuan.A survey of guidance law with terminal impact angle constraints［J］.Journal of Astronautics，2010，31（2）：315-323.（in Chinese）

［4］ Erer K S，Ozgoren M K.Control of impact angle using biased proportional navigation［C］∥Guidance，Navigation，and Control and Co-located Conferences.Boston，MA，US：AIAA，2013.

［5］ 高峰，唐胜景，师娇，等.一种基于落角约束的偏置比例导引律［J］.北京理工大学学报，2014，34（3）：277-282. GAO Feng，TANG Sheng-jing，SHI Jiao，et al.A bias proportional navigation guidance law based on terminal impact angle constraint［J］.Transactions of Beijing Institute of Technology，2014，34（3）：277-282.（in Chinese）

［6］ Kim B S，Lee J G，Han H S.Biased PNG law for impact with angular constraint［J］.IEEE Transactions on Aerospace and Electronic Systems，1998，34（1）：277-288.

［7］ Lee C H，Kim T H，Tahk M J.Interception angle control guidance using proportional navigation with error feedback［J］.Journal of Guidance Control and Dynamics，2013，36（5）：1556-1561.

［8］ Ryoo C K，Cho H，Tahk M J.Optimal guidance laws with terminal impact angle constraint［J］.Journal of Guidance，Control，and Dynamics，2005，28（4）：724-732.

［9］ Lee C H，Tahk M J，Lee J I.Generalized formulation of weighted optimal guidance laws with impact angle constraint［J］.IEEE Transactions on Aerospace Electronic Systems，2013，49（2）：1317-1322.

［10］ Xing Q，Chen W C.Segmented optimal guidance with constraints on terminal angle of attack and impact angle［C］∥50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition.Nashville，Tennessee，US：AIAA，2012.

［11］ Wang X，Wang J.Partial integrated guidance and control for missiles with three-dimensional impact angle constraints［J］. Journal of Guidance，Control，and Dynamics，2014，37（2）：644-657.

［12］ Jeon I S，Lee J I，Tahk M J.Impact-time-control guidance law for anti-ship missiles［J］.IEEE Transactions on Control Systems Technology，2006，14（2）：260-266.

［13］ 张功，李帆，赵建辉，等.弹着时间可控的机动目标多弹协同制导律［J］.指挥控制与仿真，2010，32（1）：52-55. ZHANG Gong，LI Fan，ZHAO Jian-hui，et al.Impact-time-control guidance law for multi-missile cooperative model with mobility of the target considered［J］.Command Control&Simulation，2010，32（1）：52-55.（in Chinese）

［14］ 王晓芳，郑艺裕，林海.导弹协同作战四维制导与控制一体化设计方法［J］.系统工程与电子技术，2015，37（4）：874-881. WANG Xiao-fang，ZHENG Yi-yu，LIN Hai.4D intergrated guidance and control law for missiles cooperative engagement［J］. Systems Engineering and Electronics，2015，37（4）：874-881. （in Chinese）

［15］ Jeon I S，Lee J I，Tahk M J.Homing guidance law for cooperative attack of multiple missiles［J］.Journal of Guidance，Control，and Dynamics，2010，33（1）：275-280.

［16］ 马国欣，张友根，张友安.领弹控制下的多导弹时间协同三维制导律［J］.海军航空工程学院学报，2013，28（1）：11-16. MA Guo-xin，ZHANG You-gen，ZHANG You-an.Leader-controlled three-dimensional guidance law for time-cooperative multimissiles［J］.Journal of Naval Aeronautical and Astronautical，2013，28（1）：11-16.（in Chinese）

［17］ Zhao E J，Chao T，Wang S Y，et al.An adaptive parameter cooperative guidance law for multiple flight vehicles［C］∥Atmospheric Flight Mechanics Conference.Dallas，TX，US：AIAA，2015：1-10.

［18］ 赵世钰，周锐.基于协调变量的多导弹协同制导［J］.航空学报，2008，29（6）：1605-1611. ZHAO Shi-yu，ZHOU Rui.Multi-missile cooperative guidance using coordination variables［J］.Acta Aeronautica et Astronautica Sinica，2008，29（6）：1605-1611.（in Chinese）

［19］ Zhang Y，Ma G，Liu A.Guidance law with impact time and impact angle constraints［J］.Chinese Journal of Aeronautics，2013，26（4）：960-966.

［20］ Harl N，Balakrishnan S N.Impact time and angle guidance with sliding mode control［J］.IEEE Transactions on Control Systems Technology，2012，20（6）：1436-1449.

［21］ Lee J I，Jeon I S，Tahk M J.Guidance law to control impact time and angle［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43（1）：301-310.

［22］ 王晓芳，洪鑫，林海.一种控制多弹协同攻击时间和攻击角度的方法［J］.弹道学报，2012，24（2）：1-5. WANG Xiao-fang，HONG Xin，LIN Hai.A method of controlling impact time and impact angle of multiple-missiles cooperative combat［J］.Journal of Ballistics，2012，24（2）：1-5.（in Chinese）

Cooperative Guidance Law with Impact Angle and Impact Time Constraints for Networked Missiles

ZHANG Chun-yan，SONG Jian-mei，HOU Bo，ZHANG Min-qiang
（School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China）

Cooperative biased proportional guidance law with impact angle and impact time constraints is presented for cooperative attack of networked missiles.The biased proportional guidance law with impact angle constraints is proposed，and the expression of time-to-go in this guidance law is deduced.The proportional coefficient is adjusted by the difference of the time-to-go of each missile in the network.And the cooperative biased proportional guidance law with impact angle and impact time constraints is presented. It is proved theoretically that the multiple missiles trend to have the same time-to-go by the guidance law. Finally，the mathematical simulation of guidance system of networked missiles illustrates the validity of the proposed guidance law and the expression of time-to-go.

control science and technology；cooperative guidance law；impact angle constraint；impact time constraint；time-to-go

TJ765.3

A

1000-1093（2016）03-0431-08

10.3969/j.issn.1000-1093.2016.03.007

2015-08-20

武器装备预先研究项目（51420121001）

张春妍（1992—），女，博士研究生。E-mail：zhangchunyan868@126.com；宋建梅（1968—），女，副教授，博士生导师。E-mail：sjm318@bit.edu.cn