防空武器模拟动态飞行试验方法

丁天宝，杨东，何朝，王琨

（西北机电工程研究所，陕西咸阳712099）

防空武器模拟动态飞行试验方法

丁天宝，杨东，何朝，王琨

（西北机电工程研究所，陕西咸阳712099）

为解决防空武器模拟动态飞行试验问题，提出了防空武器模拟动态飞行试验系统工作原理和方法，建立了模拟动态飞行试验目标真值数学模型、稳定试验摇摆量真值数学模型。通过某典型防空武器系统模拟动态飞行试验验证，证明了模拟动态飞行试验原理和所建立的数学模型的正确性。该方法建立了防空武器动态飞行试验系统的理论基础，模型可用于模拟动态飞行试验数据处理和误差分析。

兵器科学与技术；防空武器；动态飞行试验；真值

0 引言

动态飞行试验用于检验防空武器（高炮、弹炮结合武器）搜索、跟踪和火控系统的动态精度，同时考核高炮武器相关的战术性能和使用性能［1-2］。动态飞行试验是高炮武器研制中技术难度较大的一项试验。在外场靶场进行动态飞行试验时，通常目标采用作战飞机或航模靶机，目标真值测量设备使用光电经纬仪（经纬仪分布在数十千米范围），系统较为复杂。该试验常常受到天气、飞机、航路等条件的影响，周期长、成本高，成为制约武器系统研制的关键之一。

在室内开展模拟动态飞行试验，不仅可以避免天气、飞机、航路等因素的影响，还可提高试验研究水平，是防空武器研发人员长期以来追求的目标。据了解，发达国家非常重视动态飞行模拟试验技术研究，同时建立了相应的试验设施［3］。但是，此类技术核心对外封锁。目前，我国缺少防空武器模拟动态飞行试验系统性的理论和方法。随着未来防空装备需求的日益提高，探索新的、系统性的模拟动态飞行试验原理和方法成为当务之急。针对上述问题，本文提出了防空武器模拟动态飞行试验新原理和方法，并解决了该方法涉及的两大技术关键：模拟目标真值获取数学模型和摇摆稳定数学模型，为系统解决防空武器模拟动态飞行试验问题奠定了技术基础。

1 动态飞行试验原理

1.1动态飞行试验原理

动态飞行试验主要是为了检验检测防空武器装备的跟踪精度和火控精度，其系统原理图如图1所示。

图1　外场动态飞行试验原理图Fig.1 Schematic diagram of dynamic flight experiment

图1中：Dm为目标机斜距离（m）；βm为目标机方位角（密位）；εm为目标机高低角（密位）；Dmz为目标机斜距离真值（m）；βmz为目标机方位角真值（密位）；εmz为目标机高低角真值（密位）；βq为提前方位角（密位）；φq为射角（密位）；Yq为引信分划；βqz为提前方位角真值；φqz为射角真值（密位）；Yz为引信分划真值；Δβm、Δεm、ΔDm分别为目标机方位误差、高低误差、距离误差；Δβq、Δφq、ΔY分别为目标机提前方位角误差、射角误差、引信误差；XC、YC、ZC为目标直角坐标系下真值三维坐标。在时统设备的同步下，目标飞行轨迹（航路）的真值坐标由靶场的光电经纬仪测量；被试品数据采集设备同步获得高炮武器上雷达、红外设备及激光测距机测出目标空间坐标的一组观测值。求取对真值与观测值的一次差后进行统计，可得到动态跟踪误差和火控解算误差［4-7］。

1.2模拟动态飞行试验原理

模拟动态飞行试验原理如图2所示。图2中：D1为目标机视点斜距离（m）；β1为目标机视点方位角（密位）；ε1为目标机视点高低角（密位）；D0为目标机斜距离真值（m）；β0为目标机方位角真值（密位）；ε0为目标机高低角真值（密位）；φ0为提前方位角真值（密位）；Y0为引信分划真值；β2为目标机方位角（密位）；ε2为目标机高低角（密位）；φ2为射角（密位）；D2为目标机斜距离（m）；Y2为引信分划。

图2　模拟动态飞行试验原理图Fig.2 Schematic diagram of dynamic flight simulation experiment

模拟动态飞行试验时，由“航路生成仪”输出目标航路信息，其中目标方位角和高低角送给目标投影系统（相对于O＇（视点）），而距离送给被试品（火炮）；摇摆台模拟火炮行进过程的各种姿态变化。“数据采集系统”同步采集火炮输出的目标跟踪数据（方位角、高低角）以及“目标真值解算”输出的修正后的目标真值。“数据处理系统”处理跟踪值（观测值）与真值的一次差，再统计全航路跟踪误差和火控解算误差［8］。

因为试验条件的差异，模拟动态飞行试验与外场动态飞行试验有一定的区别，其中主要区别是：

1）目标不同。外场动态飞行试验采用真实目标；而模拟动态飞行试验的目标是投影系统投影在球幕上的模拟目标；

2）目标与被试品距离不同。外场动态飞行试验目标离火炮比较远（通常为0～20 km），而模拟动态飞行试验的模拟目标比较近（通常为12～50 m）；

3）目标真值获取方法不同。外场动态飞行试验目标真值由光电经纬仪（或精测雷达）测量得到；而模拟动态飞行试验的目标真值是通过真值解算系统获得。

正是因为上述差异，模拟动态飞行试验中必须解决“模拟动态飞行目标真值”问题，以及被试品（防空武器）“随摇摆台的牵连运动补偿数学模型”问题。这两项关键技术是防空武器模拟动态飞行试验方法的核心技术。

2 模拟动态飞行目标真值

通过以下步骤，获得模拟动态飞行试验目标坐标真值。

2.1坐标系

为了规范自行高炮武器系统数据采集、转换、处理、共享等过程，对武器系统的坐标系进行了系统性设定。

自行高炮坐标系采用左手坐标系，正北为正（X），正东为正（Y），垂直向上为正（Z）。方位角β以X轴为零位，顺时针为正；高低角ε以OXY平面为零位，向上为正，如图3所示。

图3　自行高炮坐标系Fig.3 Coordinate system of self-propelled anti-aircraft gun

图3中：OptXptYptZpt为炮塔坐标系；OsrXsrYsrZsr为搜索雷达坐标系；OtrXtrYtrZtr为跟踪坐标系；OhpXhpYhpZhp为火炮坐标系。

2.2视点坐标的确定

为了建立数学模型，假设模拟动态飞行试验设备如图4、图5所示。

图4　模拟动态飞行实验室侧视图Fig.4 Side view of dynamic flight simulation laboratory

图5　模拟动态飞行实验室俯视图Fig.5 Top view of dynamic flight simulation laboratory

首先，定义视点。视点是指设计球幕试验室时根据目标与背景生成系统、航路生成仪生成目标时所取的基准点，也就是生成的目标的原点。根据模拟试验设备的具体情况，取视点位于球幕的中心切面后方L1，摇摆台中心到球幕中心距离为L2，摇摆台直径为D，球心离地面距离为h，视点距地面高度为h1.

图5中：固定坐标系OXYZ以球心O为坐标原点，O点的坐标为（0，0，0）；视点坐标系O＇X＇Y＇Z＇，视点O＇相对于球心的坐标为（-L1，0，h1-h）；以摇摆台的摇摆平面中心建立坐标系O″X″Y″Z″，O″的坐标为（-L2，0，-h）；球幕目标由航路仪生成，投影到球幕上，目标的真值由真值解算系统（见2.4节）获得设真值为（βA，εA，DA＇）.其中，方位角βA和高低角εA由航路生成仪输出相对于视点的真值。图6为投影目标与视点的关系图。

图6　投影目标与视点的关系图Fig.6 Relation between projection target and point of view

2.3跟踪点坐标的确定

被试品以“某自行高炮武器”为试验对象，试验时被试品放置于大型摇摆台上，被试品标准状态时坐标系的相关关系如图3所示。

这种模拟动飞的跟踪，只能采用电视跟踪。因此，对于光电跟踪的跟踪坐标系，涉及到跟踪坐标系与炮塔坐标系的平移。根据坐标关系，可以得到跟踪点的具体位置表达式。

由此可知G点相对球幕中心的实际坐标为X轴、Y轴、Z轴3个方向的分量分别为

式中：X1为跟踪点G到跟踪坐标系Otr中心点X轴方向的距离；Y1为跟踪点G到跟踪坐标系Otr中心点Y轴方向的距离；Z1为跟踪点G到跟踪坐标系Otr中心点Z轴方向的距离；X2为跟踪坐标系Otr中心点到与车体坐标系Opt中心点X轴方向的距离；Y2为跟踪坐标系Otr中心点到与车体坐标系Opt中心点Y轴方向的距离；Z2为跟踪坐标系Otr中心点到与车体坐标系Opt中心点Z轴方向的距离；X3为车体坐标系Opt中心点到摇摆台的坐标系O″中心点X轴方向的距离；Y3为车体坐标系Opt中心点到摇摆台的坐标系O″中心点Y轴方向的距离；Z3为车体坐标系Opt中心点到摇摆台的坐标系O″中心点Z轴方向的距离；βG为跟踪点G到跟踪坐标系Otr固有的方位夹角；εG为跟踪点G到跟踪坐标系Otr固有的高低夹角；β（t）tr为跟踪头跟踪目标时的方位夹角；ε（t）tr为跟踪头跟踪目标时的高低夹角；β（t）pt为炮塔跟踪目标时的方位夹角。

2.4目标真值计算

目标由航路仪生成，设为目标在球幕上的投影为A＇，真值以视点坐标系O＇X＇Y＇Z＇给出坐标，A＇的真值为（βA，εA，DA＇）如图7所示。

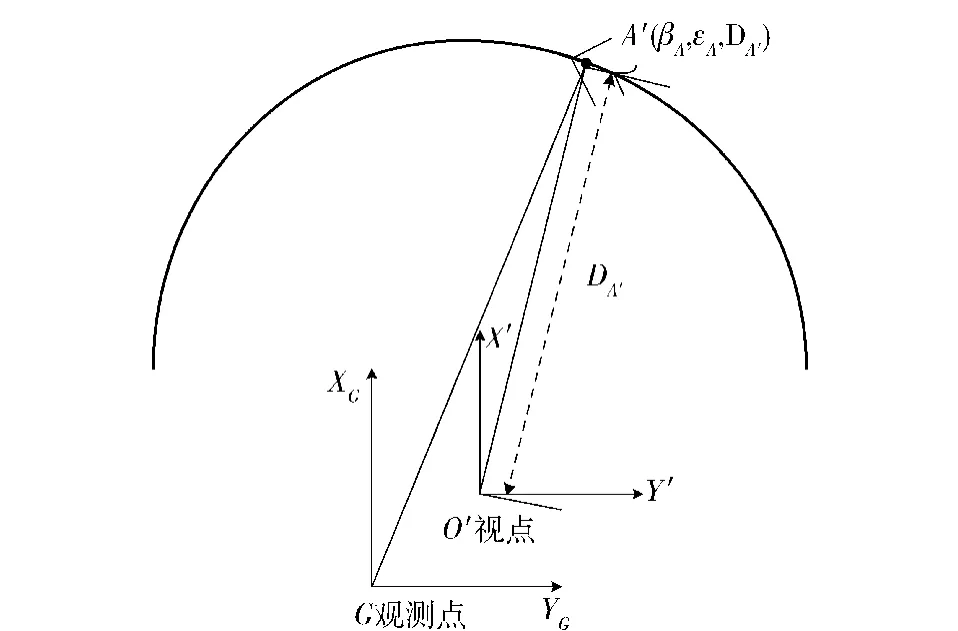
图7　目标A与视点、跟踪点的相关关系图Fig.7 Relation among target A，point of view and tracking point

图7中，DA＇为视点O＇到目标A的投影点A＇之间的距离。通过计算可求得。根据物理量之间的关系，目标A的投影A＇相对于跟踪点G在极坐标系下的坐标真值为

（4）式～（6）式为目标A在跟踪点G下的真值。

2.5动态飞行试验数据处理

模拟动态飞行试验时，由航路生成仪生成目标A，投影于球幕上为A＇.目标坐标真值以视点坐标系O＇x＇y＇z＇给出，设为（βA，εA，DA）.目标A的投影A＇相对于跟踪点G的真值坐标为（βA＇G，εA＇G，DA＇G）.由跟踪点 G测得观测值（跟踪值），设为（βGA＇，εGA＇，DGA＇）.

按照试动态飞行验数据处理方法，可计算出航路上每个采样点的误差，即方位角一次差Δβ= βGA＇-βA＇G，高低角一次差Δε=εGA＇-εA＇G.

为消除投射到幕上的动态目标（如角度）与同时输出的该目标的坐标参数（如距离）时间误差，在求一次差前，需要进行时间补偿。

根据方位角、高低角一次差，可以统计出目标跟踪系统全航路的系统误差和随机误差。同理，求取高炮系统输出的射击诸元与逆解的火控射击诸元真值，可以得到火控一次差，并统计火控系统误差和随机误差。

3 摇摆稳定数学模型及检测方法

防空武器在行进中作战时，其车体姿态和航向角不断发生变化，因此安装在其上的目标搜索系统、跟踪系统和火力线同时受到车体姿态变化等扰动的影响。如果不采取稳定措施，防空武器在行进间的毁歼概率将会大大降低。外场动态飞行试验时，利用路面产生摇摆，通过测量防空武器跟踪瞄准线的稳定数据，评判跟踪稳定系统的性能。模拟动态飞行试验时，利用摇摆台模拟武器行进间的姿态变化，通过测量防空武器跟踪瞄准线的稳定数据与理论摇摆数据，评判跟踪稳定系统的性能。因此，摇摆试验是行进间动态飞行试验内容之一，其摇摆量解算数学模型是其中的关键技术［9-11］。

3.1摇摆量真值解算数学模型

摇摆试验的原理是通过计算倾侧状态理论摇摆角真值以及同一时刻防空武器稳定跟踪器稳定补偿后的摇摆角之差，评判稳定性能。

两轴制（方位、高低）的被试品的角度补偿，用于三轴摇摆扰动引起的角度变位。

根据稳定与补偿的物理量关系，其数学关系如下：

摇摆方位角真值关系式

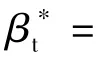
摇摆俯仰角真值关系式

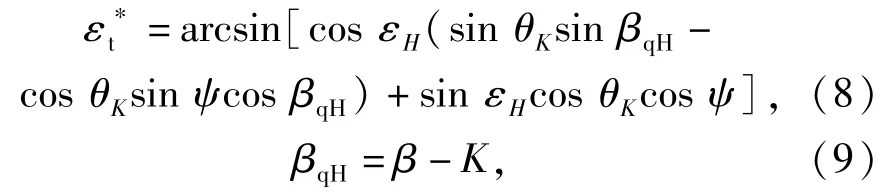
式中：βt为倾侧状态方位角；εt为倾侧状态俯仰角；β为水平状态方位全角（初始方位角）；βqH为水平状态方位角（中间量）；εH为水平状态俯仰角（初始俯仰角）；ψ为纵摇角（取自摇摆台）；θK为横滚角（取自摇摆台）；K为水平航向角（取自摇摆台）。

3.2摇摆稳定检测数据录取与处理

在摇摆台和被试品完成零位基准安装和调整后，可将被试品—稳定跟踪器予设置初始方位角β和初始俯仰角εH，用数据录取装置记录β、εH初始值。混合摇摆时数据录取装置同步录取水平航向角K、纵摇角ψ、横滚角θK（取自摇摆台），以及稳定补偿后的倾侧状态方位角βt、俯仰角

按（7）式～（9）式编制检测计算机软件，将上述同步检测的值 β、εH、K、ψ、θK注入检测计算机按（7）式～（9）式求出倾侧状态方位角真值俯仰角真值

用同一时刻录取的稳定跟踪器稳定补偿后的倾侧状态下的方位角βt、俯仰角εt与上述的真值求差：

即可得出Δβtsta、Δεtsta为稳定跟踪器稳定补偿误差。

4 模拟动态飞行试验方法验证

在进行“模拟动态飞行试验方法”验证时，以“某自行高炮武器”为试验对象，试验时该自行高炮固定于大型摇摆台上，摇摆台运动模拟车体姿态变化；由“航路生成仪”生成目标航路投影到球幕上，供自行高炮目标跟踪系统跟踪；“数据采集系统”同步采集自行高炮输出的目标光电跟踪数据（方位角、高低角）以及“目标真值解算”输出的修正后的目标真值数据。

通过计算自行高炮跟踪值与真值的一次差，可计算统计出全航路跟踪误差。通过计算自行高炮输出的火控射击诸元与逆解法所得的射击诸元真值，可计算统计火控系统误差。通过求取测量稳定跟踪器稳定补偿后的角度（方位角、俯仰角）与摇摆量真值解算数学模型计算出的真值的差值，可计算稳定跟踪器稳定补偿误差。

某自行高炮跟踪精度、火控精度、稳定精度的国家靶场动态飞行试验结果与本文模拟动态飞行试验的差异均小于6%，置信度在90%以上。上述结果说明，模拟动态飞行试验目标跟踪误差、火控解算误差、稳定跟踪器稳定补偿误差与外场动态飞行试验的结果基本一致，从而验证了模拟动态飞行试验方法的正确性。

5 结论

本文提出了模拟动态飞行试验原理和方法。通过建立目标真值数学模型，解决了目标与被试品距离较近所引起的视线误差问题；通过建立摇摆量真值解算数学模型，解决了摇摆量真值问题；解决了模拟动态飞行试验中的关键技术。通过室内半实物仿真试验，验证了模拟动态飞行原理、方法和数学模型的正确性。本文所提出的方法对防空武器动态飞行试验和研发新型防空武器系统具有一定的应用价值。

（References）

［1］ 李魁武.现代自行高炮武器系统总体技术［M］.北京：国防工业出版社，2012：505-524. LI Kui-wu.Overall technology of modern antiaircraft weapon system［M］.Beijing：National Defense Industry Press，2012：514-520.（in Chinese）

［2］ 常显奇，程永生.常规武器装备试验学［M］.北京：国防工业出版社，2007：30-40. CHANG Xian-qi，CHENG Yong-sheng.The experiment of normal weapon equipment［M］.Beijing：National Defense Industry Press，2007：30-40.（in Chinese）

［3］ Dourado A O，Martin C A.New concept of dynamic flight simulator：part I［J］.Aerospace Science and Technology，2013，30（1）：79-82.

［4］ 李魁武，丁天宝.自行高炮总体综合、集成与优化［C］∥自行高炮武器系统论文集.咸阳：西北机电工程研究所，2012：42-45. LI Kui-Wu，DING Tian-bao.Overall synthesis，integration and optimization of self-propelled antiaircraft gun［C］∥The Proceedings of Antiaircraft Gun Weapon System.Xianyang：Northwest Institute of Mechanical and Electrical Engineering，2012：42-45. （in Chinese）

［5］ 魏玮，吕启元.防空武器系统性能测试与考核系统设计［C］∥自行高炮武器系统论文集.咸阳：西北机电工程研究所，2012：710-713. WEI Wei，LYU Qi-Yuan.Performance testing and evaluation of air defense system design［C］∥The Proceedings of Antiaircraft Gun Weapon System.Xianyang：Northwest Institute of Mechanical and Electrical Engineering，2012：710-713.（in Chinese）

［6］ 赵斌，丁天宝，霍勇谋，等.基于HLA的高炮跟踪瞄准仿真系统研究［J］.计算机仿真，2009，26（5）：25-27. ZHAO Bin，DING Tian-bao，HUO Yong-mou，et al.An integrated simulation system of antiaircraft gun’s tracking and aiming based on HLA［J］.Computer Simulation，2009，26（5）：25-27.（in Chinese）

［7］ 杨维，丁天宝，赵凯.一种实时的机动目标多模型跟踪算法［J］.火炮发射与控制学报，2008，29（4）：100-103. YANG Wei，DING Tian-bao，ZHAO Kai.A real-time multi-model tracking algorithm for maneuvering target［J］.Journal of Gun Launch&Control，2008，29（4）：100-103.（in Chinese）

［8］ 费业泰.误差理论与数据处理［M］.第6版.北京：机械工业出版社，2010：33-40. FEI Ye-tai.Error theory and data processing［M］.6th ed.Beijing：China Machine Press，2010：33-40.（in Chinese）

［9］ 单东升，王阳，邱晓波，等.火炮稳定控制误差特性试验研究［J］.火炮发射与控制学报，2015，36（1）：86-90. SHAN Dong-sheng，WANG Yang，QIU Xiao-bo，et al.Experimental research on the characteristics of gun stability control error based on AR model［J］.Journal of Gun Launch&Control，2015，36（1）：86-90.（in Chinese）

［10］ 张东旭，杨平，杨峰，等.基于多体系统理论的精密检测平台空间误差建模与补偿［J］.兵工学报，2014，35（4）：501-508. ZHANG Dong-xu，YANG Ping，YANG Feng，et al.Volumetric error modeling and compensation of precision measuring platform based o multi-system theory［J］.Acta Armamentarii，2014，35（4）：501-508.（in Chinese）

［11］ 段晓敏，李杰，刘俊.空气升力对被动式半捷联平台稳定性影响分析［J］.兵工学报，2014，35（11）：1813-1819. DUAN Xiao-min，LI Jie，LIU Jun.Influence of air lift on the stability of passive partial strapdown platform［J］.Acta Armamentarii，2014，35（11）：1813-1819.（in Chinese）

New Method of Dynamic Flight Simulation Experiment for Anti-aircraft Weapon

DING Tian-bao，YANG Dong，HE Zhao，WANG Kun
（Northwest Institute of Mechanical and Electrical Engineering，Xianyang 712099，Shaanxi，China）

A new principle of dynamic flight simulation experiment for anti-aircraft weapon is presented for the simulation experiment of anti-aircraft weapon in laboratory.A mathematical model of obtaining the tagart truth values and a mathematical model of obtaining the truth values of pitch and roll positions of tracker are established.The dynamic flight simulation experiment principle and the mathematical models are verified through dynamic flight simulation experiment.The principle and the key technologies of simulating dynamic flight experiment are valuable for dynamic flight simulation experiment of anti-aircraft weapons，which will promote the research and development of new anti-aircraft weapons.The proposed method is used to establish the theoretical basis of the dynamic flying experimental system，which can be used for data processing and error analysis.

ordnance science and technology；anti-aircraft weapon；dynamic flight experiment；truth value

TJ301

A

1000-1093（2016）03-0408-06

10.3969/j.issn.1000-1093.2016.03.004

2015-04-23

西北机电工程研究所预先研究项目（2014-01-FJ1335）

丁天宝（1962—），男，研究员。E-mail：tbding@yeah.net