中国货币资产间的替代弹性估计——兼论简单加总货币量在中国的适用性问题

杜浩然 黄桂田



中国货币资产间的替代弹性估计——兼论简单加总货币量在中国的适用性问题

杜浩然 黄桂田

（北京大学经济学院 北京 100871）

本文基于Rotterdam模型、LA-AIDS模型、FD-LA-AIDS模型和PIGLOG模型对中国经验进行实证检验，选择出适合分析中国货币资产需求系统的PIGLOG模型，估计了中国货币资产间的替代弹性程度。结果显示，中国货币资产的替代程度呈现较强的波动性，且统计上不具有完全替代特征。据此，现行使用简单加总法计算的货币供应量的前提是不具备的，货币量计算的简单加总法存在局限性。

货币资产 需求系统 替代弹性 简单加总货币量

一、引 言

货币资产间的替代或互补程度，对货币当局准确把握货币总量以及合理使用政策工具调控经济运行具有重要意义。货币资产加总的合适度量、货币需求方程的稳定性、金融媒介发展的影响等重要宏观问题都受到货币资产替代性或互补性的影响。从1996年起，中国将货币供应量作为货币政策的中介目标，中国人民银行使用的货币供应量数据（M0、M1、M2）是简单加总的货币量，应用这种简单加总方法的前提条件是，不同货币资产间具有一对一的完全替代性——即相互的替代弹性恒为常数。问题的关键在于，这种简单加总货币量的前提条件是否成立？如果不具备完全替代条件，简单加总的货币供应量则不能真实反映实际的货币总量。Friedman和Schwartz（1980）指出，货币资产是具有不同“货币性（Moneyness）”的复合商品，货币供应量应是全部货币资产价值的加权求和总量。简单加总货币量只是加总的特殊情形。

基于此，Barnett（1980）较早地从货币加总的视角研究货币供应量的计量问题，运用统计指数理论和加总理论，将微观经济学的最优化问题和宏观经济学联系在一起，提出了Divisia货币总量概念。Divisia货币总量是基于货币资产不完全替代假设，对货币资产的流动性进行不同权重估计，通过加权所得的货币总量——它可以将资产的替代性嵌入到总量指标的计算中，从而使加总具有经济含义。Lucas（2000）对此予以充分肯定，指出Divisia方法提供了解决货币加总问题的最好方式。

改革开放以来，中国经济总量及经济结构发生了重大变化，伴随着金融创新的不断拓展，必将导致货币资产间的替代程度发生变动。测算中国转轨时期的货币资产替代弹性，既有助于更准确地把握转轨时期的经济和金融状况，又能为货币当局判断现有的货币总量指标是否具有适应性提供实证支撑。

本文基于Barnett（1980）研究货币资产需求微观基础的分析框架，通过需求系统分析最广泛使用的Rotterdam模型、LA-AIDS模型、FD-LA-AIDS模型和PIGLOG模型，运用迭代似不相关回归（ITSUR）估计方法及消费者理论约束条件，计算得到中国货币资产间的替代弹性。之所以选用大的货币资产需求系统而非单一的需求方程，是因为需求系统允许不同资产需求存在相互关联，能够充分反映经济中的代表性个人根据货币资产相对收益的变化而调整其资产持有的行为。另外，货币资产的替代弹性会随时间发生变化，需求系统亦能对这种变化进行监测。

二、文献综述

国外学者运用不同的方法，估计多个国家货币资产间的替代弹性。这些研究多基于Barnett（1980）提出的货币需求微观基础分析框架。这一框架将货币资产视为耐用消费品，进入经济中代表性消费者的效用函数进行优化，其价格为消费者对货币资产的持有成本。

早期的货币需求模型采用单一方程的形式，Chetty（1969）开始在流动性资产的需求分析中引入需求系统的形式，允许消费者对不同资产需求相互关联，并计算替代弹性。但是，其模型假设替代弹性为常数，限制了估计的可信性。自此，学者们开始通过货币资产的需求系统求解相关弹性。起初为了简化问题，这些研究主要运用柯布-道格拉斯、CES效用函数等参数形式，其局限性在于这些形式很难准确刻画消费者的真实偏好，并对资产间的替代或互补关系施加严格的约束。之后，学者们逐渐运用弹性函数形式（Flexible Functional Forms，简称FFF）分析货币资产的需求弹性，统计理论表明，FFF的模型可在每个数据点估计弹性，具有良好效果。总体来看，迄今为止估计需求系统的方法包括微分方法、参数方法、半非参数方法和非参数方法，每种方法包含具体的模型。①运用这些方法，很多学者对货币资产进行了需求系统建模，并对其替代弹性进行估计。

一些学者对美国的货币资产间替代弹性进行了估算。如Ewis和Fisher（1985）使用Fourier模型计算美国货币资产间的替代弹性，其结论是货币资产间的替代性（或互补性）呈现低水平、易变性，因此传统加总货币方式是不准确的。Fisher和Fleissig（1997）通过显示偏好检验得到了弱可分的货币资产组合，通过Divisia加总方法得到四种新的货币资产，之后运用动态Fourier支出系统估计了替代弹性，发现新构造的货币资产间具有较弱的替代性（替代弹性通常小于0.6），指出简单加总货币量及货币需求方程的无效性。Serletis和Shahmoradi（2005）运用美国季度数据，从对消费者最大化正则条件的违反层面比较了全局弹性的Fourier模型和AIM模型，运用估计参数计算货币资产的相关弹性，得到M2成分中均值意义上的Morishima替代弹性在-0.218和0.348之间，远小于完全替代的水平。

一些文献指出美国货币资产间的替代弹性具有系统性波动。Fisher（1992）运用Fourier模型及美国的季度数据，发现货币资产的各种弹性随时间显著波动，尤其是替代弹性在-11.466至31.882之间，呈现强烈的波动，且波动和经济周期有关。Fleissig和Swofford（1996）运用美国的月度数据，在GARP检验基础上估计动态的AIM货币需求系统，计算了美国现金资产、储蓄资产和小额定期存款间的Morishima替代弹性在0.4至1.06之间，并发现在经济衰退期间（1974-1975；1980-1982；1991）和金融去管制的时期（1980年前后）替代弹性波动增大，指出货币政策应着眼于可以内生化货币资产替代效应的货币量指标。

一些学者估算了加拿大货币资产间的替代弹性，Donovan（1978）发现加拿大大部分货币资产具有互补特性，Serletis和Robb（1986）发现加拿大货币资产间的替代弹性较低（在0.125—1.105之间）。部分学者还估算了欧洲国家货币资产间的替代弹性（Drake et al., 2003；Drake和Fleissig, 2004）。

总之，国外对于货币资产间替代弹性的研究已逐步展开，已经历了由单一方程向需求系统、由参数方法向非参数或半参数方法的研究范式转变。就替代弹性的度量而言，Morishima替代弹性逐渐替代Allen替代弹性，成为衡量替代性的主流指标。同时，这一领域的研究逐渐由发达国家转向发展中国家。

然而，对中国的货币资产需求系统却缺乏研究。尽管中国部分学者已开始用Divisia货币总量对中国货币量的计量进行研究，但现有的研究均忽视了对Divisia货币总量理论基础的探讨，没有对货币资产的替代弹性进行检测。而对中国货币资产间的替代性进行估计和分析，是决定要否修正货币量加总方法的前提。有鉴于此，本文对其进行分析和估计。

三、模型选择及验证

（一）模型简介

1、Rotterdam模型

Rotterdam模型由Theil（1965）提出，通过对消费者效用最大化条件下得到的马歇尔需求函数进行全微分再进行离散处理得到。其中，是消费者对商品i的马歇尔需求，是总支出，是商品j的价格（下同）。实际估计的模型形式为：

Barnett和Serletis（2008）指出，Rotterdam模型的出现是实证需求分析的转折点。它通过消费者需求理论而直接得到，能刻画消费者的替代矩阵，对参数的线性规定也使得其易于估计。另外，Rotterdam模型不要求代表性消费者假设，在一定程度上具有普遍性。

2、PIGLOG模型

前面的Rotterdam模型不需要代表性消费者存在，但是，大部分需求系统建模都假定代表性消费者存在，进而得到加总后的特性——PIGLOG模型（即完整的AIDS模型）就是其中的代表，由Deaton和Muellbauer（1980）提出，属于局部弹性函数形式的范畴。

PIGLOG模型是由满足消费者间一致加总充要条件的PIGLOG偏好得到的系统，模型中对数支出函数的形式为，其中：。

PIGLOG系统包含足够多的待估系数，更能给潜在真实的效用或支出函数提供合理的估计。此外，其没有对系统施加外生的线性约束，可以在更大限度上把握需求系统的整体特征。Barnett和Seck（2008）进行Monto Carlo模拟的结果显示，在表征真实的需求弹性方面，若商品替代性较低或适当高时，PIGLOG模型和Rotterdam模型的表现均很好；若替代性非常高时，PIGLOG模型的表现更好。

3、LA-AIDS模型

由于PIGLOG模型具有非线性特点，不易估计和检验，现实中常对进行线性近似，通常使用Stone价格指数的形式：（Deaton和Muellbauer, 1980）。则名义支出价格平减指数的形式为：。经过线性近似的PIGLOG模型即为LA-AIDS模型，其需要的理论约束同PIGLOG模型。

4、FD-LA-AIDS模型

FD-LA-AIDS模型是LA-AIDS模型的一阶差分形式，可以减少可能的序列相关影响，也是需求系统分析的一类重要模型。其具体形式为：

该模型需满足的约束条件仍然同PIGLOG模型。可以看到，FD-LA-AIDS模型和Rotterdam模型有着相似的结构，二者的右手变量几乎相同，只是左手变量有所差异。

下文将根据上述需求模型的形式和理论约束，对中国货币资产的需求系统进行估计。在估计中，为剔除季节性和趋势性的影响，我们加入三角函数变量和时间趋势变量，通过扩展的模型形式，希望得到更准确的估计结果。

（二）估计结果及模型选择

对于货币资产的需求系统分析，Barnett（1980）将货币资产视为耐用消费品，能为消费者提供交易媒介，满足其对流动性的偏好——因此，可以将货币资产放入代表性消费者的效用函数来进行优化。对于某种货币资产，消费者对它的需求量为对该种资产的持有量，价格为消费者的实际持有成本，其形式为，其中为基准资产的收益率，为货币资产i在第t期的收益率。

由于数据所限，本文分析的货币资产均包含在央行定义的广义货币组合M2之内，包括：现金（通货）、企业活期存款、居民活期储蓄、居民定期储蓄、企业定期存款和其他存款。对于各种货币资产的持有数量，我们用X12季调后的货币资产总量除以相对应季度中国的总人口，①得到人均持有的货币资产数量，分别表示为M0、CF、CS、TS、TF，下文依次用下标1、2、3、4、5表示。

对于货币资产收益率的选择，考虑数据的真实性和可得性，本文多采用王宇伟（2009）的界定：现金的收益率为0；活期存款的收益率为活期存款利率；居民活期储蓄的收益率为考虑了利息税之后的实际活期储蓄利率；居民定期储蓄的收益率为考虑了利息税之后的实际三年期定期存款利率；定期存款和其他存款的收益率为一年期定期存款利率。②

在这一框架中，选择基准资产很重要。所谓基准资产，是指只有储藏价值、且不提供任何交易服务和违约风险的资产。Anderson et al.（1997）指出，基准资产收益率应等于某一时期各种货币资产的收益率和评级为BAA债券收益率的最大值，再加上一个取值较小的常数。从国内研究来看，已有对中国基准资产收益率的选择，主要基于五年期定期存款利率（如左柏云和付明卫，2009）和五年期国债收益率（如王宇伟，2009）两种。在理论上，基准资产应是产生确定回报、不提供任何流动性服务的资产。对于五年期国债收益率而言，该数据的时间序列2002年才有权威的发布，王宇伟（2009）构造的五年期国债收益率来自“北方之星”数据库，且在11个季度中使用5年期国债票面利率近似，准确程度有待商榷。基于此，我们参考左柏云和付明卫（2009）的方法，选用全部货币资产收益率的最大值——五年期存款利率加上1个百分点作为基准资产的收益率。③

我们进一步计算各时期不同货币资产的实际持有成本。持有成本衡量的是和仅提供储藏价值的基准资产相比，人们持有可以提供流动性的货币资产、享受流动性服务的机会成本，其形式为。本文研究的时间区间为1993年第一季度至2013年第四季度，原始数据来自《中国人民银行统计季报》。

下面将根据四个需求系统的估计结果，由理论约束满足的情况选择最优的模型。估计结果均是使用SAS/IML语言编程，通过SAS9.3软件得到。对于Rotterdam模型、LA-AIDS模型和FD-LA-AIDS模型，为了避免奇异性问题（Singularity problem），我们删除了系统中的TF方程，通过理论约束推导出此方程中相关参数。统计理论表明，删除系统中的哪个方程对于最终的结果没有影响。另外，我们对所有的价格变量进行了去均值化处理。

在系统估计过程中我们均采用迭代似不相关回归（ITSUR）方法，④其运用迭代方式，通过似不相关回归方法对联立模型进行参数估计。似不相关回归（SUR）又称联立广义最小二乘法或Zellner估计，是对多方程系统OLS估计的一般形式，其允许各方程存在不同自变量，为统计建模带来很大的灵活性。同时，SUR在参数估计过程中考虑了不同回归扰动项的潜在相关，使参数估计效率在一定情况下较对每个方程分别进行OLS回归更有效。

在运用ITSUR方法对Rotterdam模型、LA-AIDS模型、FD-LA-AIDS模型的估计中，除了用来计算TF方程中参数的几个约束条件外，还需要施加如下理论约束：

齐次性约束：

上述三个系统的估计结果显示，大部分参数都显著；运用ITSUR方法分别经过12、15、19次迭代达到了收敛的标准（0.00001）。不同模型的系统加权R方不同，LA-AIDS模型最高，为0.9837，Rotterdam模型最低，为0.5453，体现了不同模型拟合现实数据能力不同。三个模型的系统加权均方误差均接近1。

对于PIGLOG模型的估计，为了增加估计的有效性，仍剔除TF需求方程进行估计。但由于PIGLOG模型的非线性特点，在构造价格平减指数时需要引入和，其余TF需求方程中的参数可以通过理论约束求得。模型估计中需要施加的约束条件为：

估计结果显示，在PIGLOG模型系统中，绝大多数参数都在1%水平上高度显著。以0.00001为收敛的标准，PIGLOG模型经过了37次迭代实现收敛，其中包含了6次子迭代。

由于以上结果源自带有理论约束的计量模型，为满足消费者效用最大化的假设，我们必须对估计结果是否满足加总约束、齐次性约束和对称性约束进行检验，一般认为，对理论约束的检验是需求系统分析的核心环节。由于每个模型都具有若干个约束，对每个约束单个进行检验意义不大，因此我们参照Paraguas和Kamil（2006）的方法，考虑对系统是否满足以上约束进行联合性检验。其中，对于线性形式的Rotterdam模型、LA-AIDS模型、FD-LA-AIDS模型，我们根据有无约束条件下的R方构造F统计量，表示为：

对于非线性形式的PIGLOG模型，根据有无约束条件下的目标值（Objective value）构造卡方统计量，其形式为：

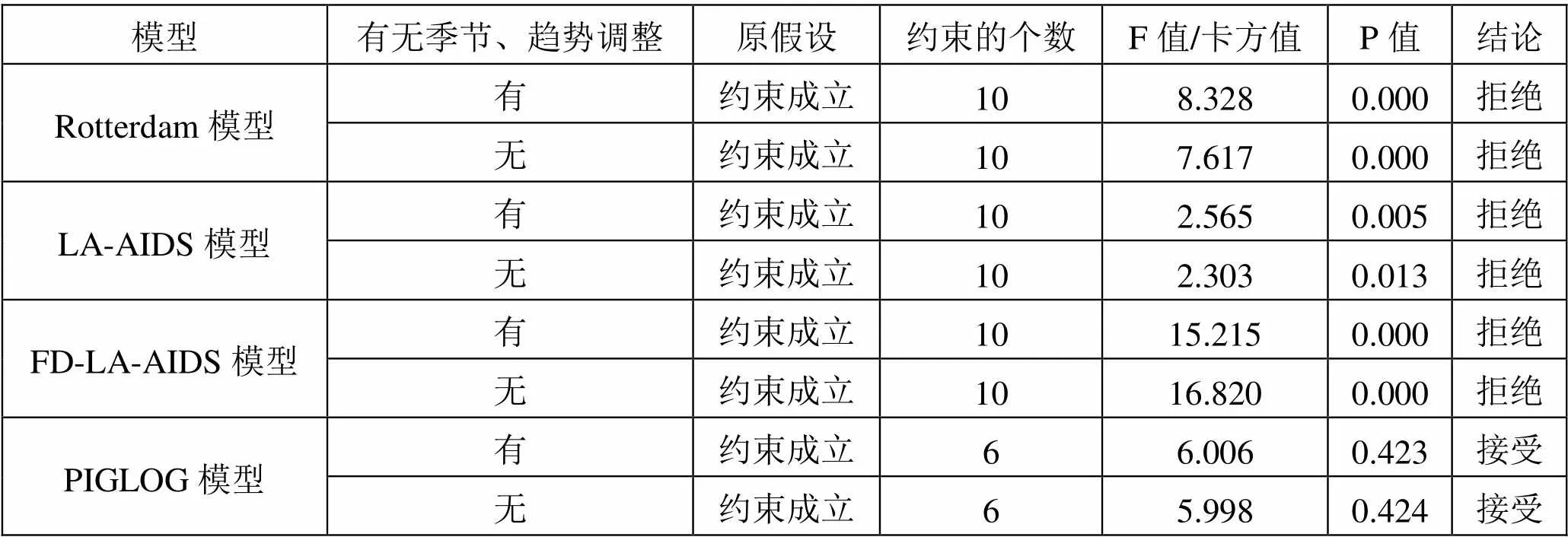
表1 对四个模型的联合约束检验

可以看出，无论是有无季节、趋势调整，对Rotterdam模型、LA-AIDS模型、FD-LA-AIDS模型的联合约束检验结果均高度显著，因此应拒绝理论约束成立的原假设。这表明，消费者效用最大化的理论条件在这三个模型中不成立。而对于PIGLOG模型，对于有季节、趋势调整的情况，联合约束检验的P值为0.423；对于无季节、趋势调整的情况，联合约束检验的P值为0.424，在10%的水平上均无法拒绝理论约束成立的原假设。因此，PIGLOG模型满足效用最大化的理论条件，能刻画中国消费者对于货币资产理性选择的特征。这一结论可以吻合Barnett和Seck（2008）进行Monto Carlo模拟的结果。

下文中将使用加入季节、趋势调整的PIGLOG模型估计得到的参数计算相关弹性。

四、中国货币资产的弹性估算

（一）货币资产支出弹性、价格弹性的计算

我们首先计算的是货币资产的支出弹性和价格弹性。给定代表性消费者在5维空间上对货币资产的马歇尔需求函数，是消费者对于货币资产i的支出弹性（也称收入弹性）。对于货币资产i和j而言，是i对j的马歇尔价格弹性：若，称为i（j）的自价格弹性；若，则称为i对j的交叉弹性。

在PIGLOG模型中，对于上文设定的形式，支出弹性和价格弹性的计算公式①为：

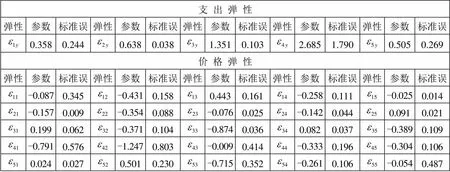
表2 货币资产的支出弹性和价格弹性

注：1、下标1至5依次代表：现金（通货）、企业活期存款、居民活期储蓄、居民定期储蓄、企业定期存款和其他存款。2、这里的弹性值为样本期间内的平均值。

由表2可以看出，所有货币资产的支出弹性均为正数，因此均为正常品。平均来看，现金（M0）、企业活期存款（CF）、企业定期存款和其他存款（TF）的支出弹性小于1，在提供流动性方面具有必需品特性；居民活期储蓄（CS）和居民定期储蓄（TS）的支出弹性大于1，在提供流动性方面具有奢侈品特性，这和我们的直觉相符，因为居民储蓄本身的作用主要在价值储藏上。

就动态特征而言，居民活期储蓄和居民定期储蓄的支出弹性水平高于其他弹性，且剔除异常值后基本保持平稳，这表明随着可配置流动性的增加，在中国代表性个人的流动性资产配置上，居民储蓄相较现金等其他货币资产而言占据更大的比例。我们认为，这和金融创新带来储蓄存款的形式多样化密切相关——这些金融创新包括银行卡、互联网支付、大额可转让定期存单等，增加了居民对于活期储蓄和定期储蓄提供流动性交易的需求，降低了对现金等货币资产的需求。此外，现金、居民活期储蓄的支出弹性有下降趋势；企业定期存款（和其他存款）的支出弹性有上升趋势；企业活期存款的支出弹性呈周期性波动。

就马歇尔价格弹性而言，我们分别考察自价格弹性和交叉弹性。首先可以看到，所有五种货币资产的自价格弹性均为负，分别为-0.087、-0.354、-0.874、-0.333和-0.054，表明货币资产的价格和需求量间的负相关关系，符合需求曲线斜率为负的理论前提。同时看到，所有货币资产对于自身价格都缺乏弹性，在数学上体现为自价格弹性的绝对值小于1。

其次，可以发现货币资产有14个交叉弹性为负，6个交叉弹性为正，一定程度体现了中国货币资产间的替代或互补特性。就数值而言，大部分交叉弹性的绝对值小于1，表明消费者的货币资产需求对于其他资产的价格缺乏弹性。另外，流动性更强的货币资产具有互补特性，如、、、均为负，这和Serletis和Shahmoradi（2005）的发现一致。但如果考虑到收入效应，这里的结论并不能充分反映中国货币资产的替代和互补特性，下文计算的替代弹性能更好地说明这一点。

（二）货币资产间替代弹性的计算

经济学界对替代弹性的含义进行了广泛讨论。传统的替代弹性是Allen替代弹性，其考虑了收入效应，测量了在保持消费者效用水平不变的前提下货币资产间的净替代程度，用Slutsky方程对称的交叉替代项弹性表示，计算公式为：

本文同时计算两种替代弹性，但侧重学界更认可的Morishima替代弹性解读中国货币资产间的替代关系以及程度。计算结果如表3所示。

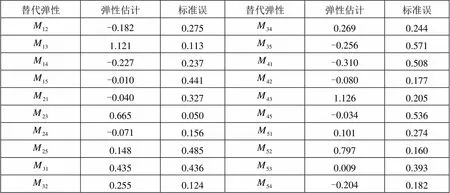
表3 货币资产间的Morishima替代弹性

注：1、下标1至5依次代表：现金（通货）、企业活期存款、居民活期储蓄、居民定期储蓄、企业定期存款和其他存款。2、这里的弹性值为样本期间内的平均值。

Morishima替代弹性估计结果显示，总体而言，不同货币资产间的替代程度存在很大差异。就符号而言，可以发现，现金与企业活期存款、现金与居民定期存款、企业活期存款与居民定期存款、居民定期存款与企业定期存款（和其他存款）具有互补的性质，替代弹性在-0.31和-0.03之间；而现金与居民活期存款、企业活期存款与居民活期存款、企业活期存款与企业定期存款（和其他存款）、居民活期存款与居民定期存款具有替代的性质，替代弹性在0.15和1.13之间。运用Allen替代弹性指标同样得到上述有关货币资产替代和互补的定性结论，表明结论是稳健的。对于其他任意两种货币资产而言，则不具有明确的替代、互补性质。

就Morishima替代弹性的数值大小而言，可以发现各不相同。就统计特征来看，大部分替代弹性不显著，只有、、、、是显著的——这些都是前面提到的替代资产的弹性；另外，互补资产替代弹性均不显著。以上结论表明，中国大多数货币资产间存在较小的关联程度，且替代性较互补性而言显著得多，这和我们的直觉是符合的。另外可以发现，和、、、、相对应的Allen替代弹性也较为显著，是对前述结论的稳健性检验，但是总体来看，Allen替代弹性有过度显著的倾向。

如果用替代弹性的标准差衡量货币资产间的替代性波动，以标准差为0作为原假设进行假设检验，发现20个检验P值都小于0.0001，均应拒绝原假设，表明中国货币资产间的替代程度具有系统性波动。①对中国而言，替代弹性的波动更多源于中国长期以来的经济发展和金融创新，会直接影响经济中的流动性以及货币政策的实施效果。特别是在2000年以前，不同货币资产的替代程度存在过山车似的波动，这和当时的金融市场化程度低、政府干预银行决策等事实有很大关系。因此，央行在货币政策的制定中，应对货币资产替代程度的系统性波动进行考虑，将其作为监测金融环境稳定的晴雨表。

表4 对货币资产完全替代性的检验结果

注：下标1至5依次代表：现金（通货）、企业活期存款、居民活期储蓄、居民定期储蓄、企业定期存款和其他存款。

表4是对货币资产完全替代性的检验结果。传统的简单加总货币量将不同货币资产视为一比一完全替代，不考虑货币资产的相互关联以及流动性的差异。理论表明，如果两种货币资产i和j是完全替代的，则样本区间的所有替代弹性M都应在统计上等于常数1。表4的前两列是原假设为均值等于1的假设检验结果，显示所有检验均强烈拒绝均值为1的原假设，表明在均值意义上，所有货币资产间的替代弹性不等于1，即不具有完全替代特征。最后一列是统计上显著不等于1的弹性百分比。例如，在5%的检验水平上，至少在23.8%样本区间内的——即现金与居民活期存款之间的替代弹性显著不等于1。同理可以发现，所有货币资产间替代弹性都有相当大的比例不满足完全替代的特征，甚至还有多个替代弹性在全部样本区间落在弹性等于1的置信区间之外。

由此可见，货币资产在中国不具有完全替代性。因此，对于货币加总，假定货币资产完全替代的简单加总货币量不具有理论基础，是度量货币总量的劣等指标。要说明的是，本文重点在于估计中国货币资产间的替代弹性，其结果可以在理论上反映经济和金融的稳定，作为中介指标被央行和宏观经济部门观测。同时，我们兼论了简单加总货币量的使用前提是不具备的。当前，货币量的简单加总方法已沿用多年，且应用范围较广；加上Divisia货币总量内涵专业性强，对于有关数据要求高，相对较难与公众沟通，因此尚未得到全面普及。但在现实的经济运行中，IMF在2008年对Divisia货币总量的特征进行了全面阐述，英格兰银行以官方形式发布这一指标，同时美国（圣路易斯银行）、以色列等国计算并发布这一数据，日本、欧盟将这一指标纳入宏观监控体系。鉴于货币供应量在中国经济的重要地位，我们认为应当在适宜时机推动中国货币总量指标的完善，将可行的Divisia货币总量作为简单加总货币量的补充性指标，被央行、学界、业界所利用，并逐步向公众普及，帮助他们更专业和准确地判断和分析宏观经济形势，保证货币政策的适当效果。

五、结论及政策建议

本文是对中国货币资产间替代弹性的系统估计，使用Barnett（1980）研究货币资产需求微观基础的框架，运用中国1993至2013年的季度数据进行分析，得到的主要结论如下：

第一，对于微观需求系统分析最广泛使用的Rotterdam模型、LA-AIDS模型、FD-LA-AIDS模型和PIGLOG模型的适用性问题，通过对模型必需的理论约束进行检验，发现只有PIGLOG模型满足必需的对称性约束和齐次性约束，是揭示中国货币资产需求系统的合适模型。因此，运用PIGLOG模型估计得到的参数计算弹性是适合中国条件的。

第二，运用PIGLOG模型的估计参数，得到了中国货币资产的Allen替代弹性和Morishima替代弹性。长期静态的结果显示，不同货币资产的替代程度存在很大差异：现金与企业活期存款、现金与居民定期存款、企业活期存款与居民定期存款、居民定期存款与企业定期存款（和其他存款）具有互补性质；而现金与居民活期存款、企业活期存款与居民活期存款、企业活期存款与企业定期存款（和其他存款）、居民活期存款与居民定期存款则具有替代性质。

第三，就替代弹性的动态特征而言，中国货币资产间的替代程度具有较强的系统性波动，不仅如此，无论是均值检验，还是计算显著不完全替代的百分比，均发现中国的货币资产不具有完全替代性，因此长期以来使用简单加总货币量的理论前提是不具备的。

货币当局制定和执行相关政策，必须运用合理的指标，以对经济中的长短期现状有准确的把握。一方面，本文估计的货币资产间替代弹性可以反映经济和金融是否稳定，作为中介指标被央行和宏观经济部门观测。另一方面，当前中国央行将货币供应量作为重要的调控工具，应选择具有理论基础、对宏观经济变量有更好指示和预测作用的货币加总指标。本文的结论显示，中国的货币资产不具有完全替代的特性，因此当前央行运用的简单加总货币量不具有理论基础。而Divisia货币总量考虑了由于持有成本变化导致货币资产间的替代或互补特性，以及这种特性的系统性波动。因此，研究在欧美等国已启用的Divisia货币总量指标是否在中国适用就具有紧迫感，有关内容将另文讨论。

1. 王宇伟：《货币的加总方法对货币需求稳定性的影响》[J]，《金融研究》2009年第3期。

2. 左柏云、付明卫：《中国货币服务指数的构建和经验检验》[J]，《金融研究》2009年第11期。

3. Anderson, R., Jones, B., and Nesmith, T., 1997, “Building New Monetary Services Indexes: Concepts, Methods and Data”[J],, Vol. 79, No. 1: 53-82.

4. Barnett, W. A., 1980, “Economic Monetary Aggregates: An Application of Index Number and Aggregation Theory”[J],, Vol. 14, No. 1: 11-48.

5. Barnett, W. A., and Seck, O., 2008, “Rotterdam Model versus Almost Ideal Demand System: Will the Best Specification Please Stand Up?”[J],, Vol. 23, No. 6: 795-824.

6. Barnett, W. A., and Serletis, A., 2008, “Consumer Preferences and Demand Systems”[J],, Vol. 147, No. 2: 210-224.

7. Blackorby, C., and Russell, R. R., 1989, “Will the Real Elasticity of Substitution Please Stand Up?”[J],, Vol. 79, No. 4: 882-888.

8. Chetty, V. K., 1969, “On Measuring the Nearness of Near-moneys”[J],, Vol. 59, No. 3: 270-281.

9. Deaton, A. S., and Muellbauer, J. N., 1980, “An Almost Ideal Demand System”[J],, Vol. 70, No. 3: 312-326.

10. Donovan, D. J., 1978, “Modeling the Demand for Liquid Assets: An Application to Canada”[J],, Vol. 25, No. 4: 676-704.

11. Drake, L., and Fleissig, A. R., 2004, “Semi-Nonparametric Estimates of Currency Substitution: The Demand for Sterling in Europe”[J],, Vol. 12, No. 3: 374-394.

12. Drake, L., Fleissig, A. R., and Swofford, J. L., 2003, “A Semi-Nonparametric Approach to the Demand for UK Monetary Assets”[J],, Vol. 70, No. 277: 99-120.

13. Ewis, N. A., and Fisher, D., 1985, “Toward a Consistent Estimate of the Demand for Monies: An Application of the Fourier Flexible Form”[J],, Vol. 7, No. 2: 151-174.

14. Fisher, D., 1992, “Money-Demand Variability: A Demand-Systems Approach”[J],, Vol. 10, No. 2: 143-151.

15. Fisher, D., and Fleissig, A. R., 1997, “Monetary Aggregation and the Demand for Assets”[J],, Vol. 29, No. 4: 458-475.

16. Fleissig, A., and Swofford, J. L., 1996, “A Dynamic Asymptotically Ideal Model of Money Demand”[J],, Vol. 37, No. 2: 371-380.

17. Friedman, M., and Schwartz, A. J., 1970, Monetary Statistics of the United States: Estimation, Sources, Methods, and Data[M]. New York: Columbia University Press.

18. Lucas, R. E., 2000, “Inflation and Welfare”[J],, Vol. 68, No. 2: 247-274.

19. Paraguas, M. D. S., Kamil, A. A., 2006, “Model Selection of Meat Demand System Using the Rotterdam Model and the Almost Ideal Demand System(AIDS)”[J],, Vol. 5, No. 2: 529-537.

20. Serletis, A., Robb, A. L., 1986, “Divisia Aggregation and Substitutability Among Monetary Assets”[J],, Vol. 18, No. 4: 430-446.

21. Serletis, A., Shahmoradi, A., 2005, “Semi-Nonparametric Estimates of the Demand for Money in the United States”[J],, Vol. 9, No. 4: 542-559.

22. Theil, H., 1965, “The Information Approach to Demand Analysis”[J],, Vol. 33, No. 1:67-87.

①对这些方法的详细说明，参见Barnett和Serletis (2008)。

①本文假设人口在一年内以固定增长率进行增长，可以根据年末人口数据推算季末的相应数据。

②王宇伟（2009）对于企业定期存款和其他存款，以及居民定期存款均选用三年期定期存款表征。我们之所以选择不同期限的利率，是考虑到企业在资金周转方面可能具有相对居民更强的流动性偏好，因此选用一年期定期存款利率表征企业定期存款和其他存款的收益率。

③本文也运用了王宇伟（2009）使用的五年期国债收益率作为基准资产收益率进行了稳健性检验，根据理论约束仍选择出了PIGLOG模型，同时对弹性的估计结果并无很大差异。

④由于篇幅所限，我们不详细汇报这里的估计结果，有兴趣的读者可以向作者索取。

①参见Barnett和Seck (2008)。

①我们绘制了中国货币资产间Morishima替代弹性的动态示意图，有兴趣的读者可以向作者索取。