区间值模糊图和模糊拟阵
2016-10-13丁毓谢建明李小南
丁毓,谢建明,李小南*
区间值模糊图和模糊拟阵
丁毓,谢建明,李小南*
(西安电子科技大学数学与统计学院,西安市邮编;710071)
图与拟阵有着密切的联系。本文研究区间值模糊图与模糊拟阵之间的关系。对于任意一个区间值模糊图,通过区间排序诱导出一个模糊图。由截模糊图得到一系列分明图,又因为每个分明图都可以得到一个圈拟阵,从而可获得拟阵序列。最后由拟阵序列构造出一个模糊拟阵。最后指出区间值模糊图和模糊拟阵之间不存在一一对应关系。
区间排序;区间值模糊图;模糊拟阵;拟阵序列
引言
自1965年Zadeh[1]提出模糊集合的概念以后,诸多的数学工作者开始致力于模糊集合的数学理论研究,开辟了许多模糊数学的研究方向和领域。现在模糊集合几乎渗入了基于经典集合论的所有纯数学分支中,如拓扑、代数、几何、算术、测度论、概率论、范畴论等。在1975年,Zadeh[2]提出了区间值模糊集的概念。同年,作为欧拉图论的一个分支,Rosenfeid[3]提出了模糊图的概念、定义了模糊集之间的模糊关系,并将分明图论中许多概念和结论推广到了模糊图理论中。此后国内外不少学者也都致力于模糊图理论的研究,提出了许多新见解、新理论、新方法。关于模糊图理论及应用方面的进展可参见文献[4]。之后,许多学者提出了各种模糊集的推广理论。例如,区间值模糊集和直觉模糊集是模糊集合的两种重要的推广,且这两种模糊集的推广理论现在已经和图论的研究结合在了一起,参见Akram和Dudek[5]。
拟阵首先由Whitney[6]提出。作为同时推广了图和向量空间中的某种独立结构,拟阵和图及向量空间有着密切的关系。1988年,Goetschel和Voxman[7]首次定义并研究了模糊拟阵。既然图和拟阵有如此密切的联系,那么研究模糊图包括区间值模糊图和直觉模糊图,与模糊拟阵的联系就是非常自然的事情了。本文将研究区间值模糊图和模糊拟阵之间的联系。
本文首先考虑区间的排序问题,通过某种规则将区间值模糊图中的边排序,然后根据边的权序截得到一列分明图,进而得到一列分明拟阵。根据模糊集的分解定理,可由分明拟阵列构造一个模糊集族,最后证明了这个模糊集族构成一个模糊拟阵。这样就建立了区间值模糊图和模糊拟阵之间的联系。
1 预备知识

定义1.1 设U是论域,称映射

定义1.2 (Oxley[8]) 拟阵是这样一个二元组(),其中E是一个有限的集合,I是集合E的一个非空子集族,且满足以下两个条件:
设M=(E,I)是一个拟阵。集合I中的元素被称作拟阵M的独立集。
定义1.3 (Goetschel和Voxman[7]) 设X是一个有限集,且是一个非空的模糊集族,满足以下条件
定义1.4 设是一个非空有限集合,是由中元素组成的无序对,则称(,)为一个(分明)图。中的元素称为图的顶点,中的元素称为边。
定义1.5 区间值模糊图[5]:设是一个非空有限集,是的子集。设,分别是和上区间值模糊集,且满足

(4)
2 区间值模糊图诱导模糊拟阵
特别地:

图1 区间值模糊图G=(A,B)
模糊图是一种特殊的赋权图,而区间值模糊图又是模糊图的推广,权值由点变为区间。对于一个区间数,取其点为代表元(根据不同的实际情况可适当取值,一般情况下可取=1/2),用代表元来表示这个区间数,则区间值模糊图G=(A,B)可以表示为成为一个模糊图=,称之为由区间值模糊图诱导出的点模糊图。
例2.1 设=(,)(如图1所示)是一个区间值模糊图,求它诱导的模糊图。取0.5 。
注意本文所涉及的集合都是有限集,因此由模糊图诱导出的拟阵的个数也是有限的。通过命题2.1 还可以得出下面的推论。
注2.1 区间值模糊图每条边的权值为区间。这里 采用的是区间数的序,而且前面已经指出 常常取为1/2。这样就产生了两个问题:
1.若采用其它的区间数排序方法,也会得到相应的分明图序列从而产生分明拟阵序列,那么这样得到的拟阵序列和采用本文中用到的方法有何区别?
2.本文中取为1/2,那么若取其它值,得到的分明拟阵列会不同吗?
对于第一个问题,也即采用其它的区间数排序法来讨论区间值模糊图和模糊拟阵的联系,将是 以后的一个研究课题。对于第二个问题, 很容易举例说明,取值不同,得到的分明拟阵序列有可能不同。
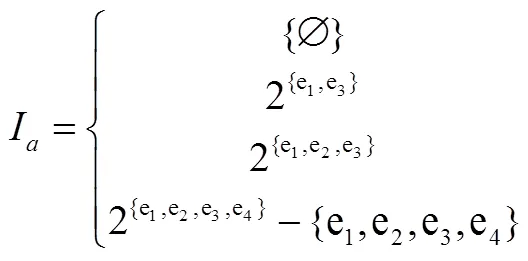
所以,对于任意的一个区间值模糊图=(,),其诱导的点模糊图为,取其基础序列中的每一个数(),都可以截得一个分明图,是分明图的圈拟阵,其独立集族为,令。则,…,是上的拟阵序列,且满足条件,其中。
在接下来的例子中将会发现对于不同的区间值模糊图,却有可能诱导出相同的拟阵序列。
例2.3考虑图4中的两个区间值模糊图(a)和(b)。

(a) (b)

图5 模糊图(a)和(b)诱导的模糊图

任意给一个区间值模糊图G=(A, B),就会存在唯一的一个拟阵序列与之对应。而又可以由模糊集的分解定理:设是一个论域U上的模糊集,对于任意的,有可得。如果知道一个模糊集的所有a-截集,那么就可以通过它的a-截集来反过来求出这个模糊集。
解:

故
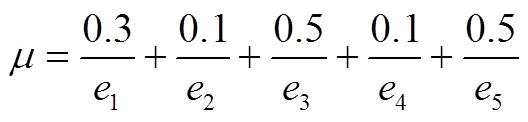
由上述的讨论知道,任意给一个区间值模糊图,都可以得到其全部由a-截得的独立集序列(有限)。因此可以用模糊集的分解定理构建一个“模糊独立集族”(类似例2.4的方法)。接下来给出一个例子来详细说明。
例2.5依然考虑例2.1中的区间值模糊图。
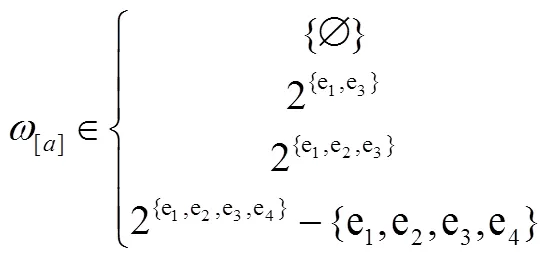
证明:区间值模糊图G=(A,B)的每条边的权值为区间。根据定义2.1中介绍的区间的排序,可知此区间值模糊图在经过排序后可以看作等价于一个模糊图,即此时边的权值为[0,1]中的数。由前所述,此时可以诱导出一个分明图列,进而诱导出以个拟阵序列。由命题2.1这样的拟阵序列是单调的。最后由[7]中定理2.3可知是某个模糊拟阵的模糊独立集族,即是一个模糊拟阵。
3 区间值模糊图和模糊拟阵的对应关系
上节给出了从区间值模糊图构造模糊拟阵的方法,本节指出区间值模糊图和模糊拟阵不是一一对应的。下面 先看一个例子。
例 3.1 考察图6和图7中的两个区间值模糊图。设图6导出的模糊拟阵为。则容易验证
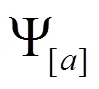
图 6 区间值模糊图G

图7 区间值模糊图G2
注 3.1 本文中所提出的从区间值模糊图导出模糊拟阵的方法是建立在区间值数的排序法基础上的()。本节给出了两个不同区间值模糊图导出同一个模糊拟阵的例子,其实 还可以给出不同的区间值模糊图由取不同值而导出同一个模糊拟阵的例子。
4 结语
模糊图理论是经典图论的推广。目前在模糊图论的应用领域的研究已经极为广泛,比如聚类分析、系统分析、神经网路、地理信息系统等。区间值模糊图则是模糊图论的一个重要推广,在某些问题上有一些较模糊图更好的性质。本文研究了区间值模糊图与模糊拟阵之间的关系。任意给一个区间值模糊图G=(A,B),提出了一种构造模糊拟阵的方法。下面列出下一步要进行的工作:
(1) 如前所述,本文从区间值模糊图构造模糊拟阵的关键一步是对区间数排序。现在已有许多区间数排序的方法,那么用不同于本文所采用的序法从区间值模糊图出发所得到的模糊拟阵与本文中的模糊拟阵有何关系?
(2) 现在已经有多种图的推广理论,例如模糊图,直觉模糊图、区间值直觉模糊图等(参考[10])。是否可以由这些图的推广理论用类似本文的方法诱导出模糊拟阵?
(3)G-V模糊拟阵的研究已经取得了很多重要成果(参考[11,12])。研究基于区间值模糊图的导出拟阵的性质是一个值得研究的课题。
[1] Zadeh L A. Fuzzy sets [ J]. Information Control, 1965, 8: 338- 353.
[2] Zadeh L A. The concept of a Linguistic variable and its application to approximate reasoning I [ J ]. Information Science, 1975, 8: 199- 249.
[3] Rsenfeld A. Fuzzy graphs[ C ] / / Zadeh L A, Fu K S, Shimura M. Fuzzy sets and their applications. New York: Academic Press, 1975: 77- 95.
[4] Mordeson J N, Nair P S. Fuzzy graphs and fuzzy hypergraphs (second edition) [M ]. Heidelberg: Physica Verlag , 2001.
[5] Muhammad Akram, Wieslaw A.Dudek. Inter-valued fuzzy graphs[J]. Computers and Mathematics with Applications, 2011, 61(2):289-299.
[6] Whitney H. On the abstract properties of linear dependence, American Journal of Mathematics 57(1935):251-256.
[7] Goetschel R, Voxman W, Fuzzy matroids, Fuzzy Sets and Systems 27 (1988): 291-302.
[8]. Oxley J G, Matroid Theory, Oxford University Press, New York, 1992.
[9] 孙海龙,姚卫星.区间数排序方法评述[J].系统工程学报,2010, 25(4) 304-312.
[10] Atanassov K.T. On intuitionistic fuzzy sets theory, Springer-Verlag, Berlin, 2012.
[11] Li X N, Yi H J, Axioms for fuzzy bases of Hsueh fuzzy matroids, Journal of Intelligent & Fuzzy Systems 29 (2015):1995-2001
[12] Li X N, Yi H J, Fuzzy bases of fuzzy independent set systems, Fuzzy sets and systems, Inpres
Interval-Valued Fuzzy Graphs and Fuzzy Matroids
DING Yu, XIE Jianming, LI Xiaonan
(College of mathematics and statistics, Xidian University, 710071, China;)
Graphs and matroids have a close relationship. In this paper, we study the relation between interval valued fuzzy graph and fuzzy matroid. For any interval valued fuzzy graph, it can induce a fuzzy graph by interval ordering. And then a sequence of crisp graphs can be obtained by cuts of the fuzzy graph. Since a crisp graph can induce a cycle matroid, a sequence of matroids will be constructed. We finally construct a fuzzy matroid from the induced sequence of matroids. Finally, we point out that there is no one-to-one correspondence between interval-valued fuzzy graphs and fuzzy matroids.
Interval ranking; interval-valued fuzzy graph; fuzzy matroids; matroid sequence
672-9129(2016)01-0001-05
O151
A
2016-06-14;
2016-06-23。
国家自然科学基金青年基金(No.61202178)。
丁毓(1993-),女,新疆伊犁人,2016级硕士;谢建明(1990-),男,新疆石河子人,2015级硕士;李小南(1981-),男,陕西西安人,副教授,主要研究方向:拟阵推广理论、粗糙集及三支决策。
(*通信作者电子邮箱:lxn2007@163.com)
