一阶欧拉型型无界时滞中立型微分方程解的振动准则

王媛，申建华



一阶欧拉型型无界时滞中立型微分方程解的振动准则

王媛1，申建华2

（1. 中南林业科技大学理学院，湖南长沙 410004； 2. 杭州师范大学理学院，浙江杭州 310036）

研究了欧拉型无界时滞中立型微分方程解的振动性，现有文献只对c=0, n=1时的情况进行了讨论，应用时会有局限。为了拓宽此方程的应用范围，将条件拓宽至n的一般情形，通过建立其相应的“特征方程”，得到了所有解振动的充分必要条件，并由此出发，建立了一些显式充分条件，所得结果改进和推广了原有文献的结论。

振动性；中立型微分方程；无界时滞；欧拉型

1 研究意义

数学中所研究的函数是反映客观现实世界运动过程中量与量之间的一种关系。在大量的实际问题中会遇到一些复杂的运动过程，这导致无法直接写出反映运动规律的量与量之间的关系，但建立起这些变量和它们的导数之间的关系却比较容易。这一事实正是现代应用数学研究人员和工程人员应用微分方程解决实际问题的理论依据。微分方程在物理学、力学、控制、经济学和管理科学等实际问题中具有广泛的应用。近年来，随着机器人的快速发展，微分方程在人工智能和数据挖掘，尤其是深度学习等领域具有越来越重要的作用，因此研究微分方程的解具有理论和实际的双重意义。

关于常系数和常时滞的中立型微分方程

[, (1.1)

解的振动性的研究已取得了相当丰富的结果[1-6], 这里，特别地，Kulenovic, Ladas等[3]根据其特征方程，证明了下述定理。

定理A 方程（1.1）的所有解振动当且仅当

. (1.2)

近年来，已有一些文献[7-9]研究了下列具有变系数和变时滞的中立型微分方程

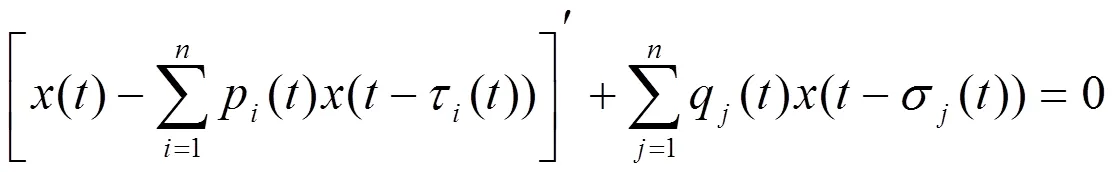
安冉[10]研究了下列欧拉型无界时滞微分方程

定理B方程（1.4）的每一个解振动当且仅当

在文[10]中，作者也给出了方程（1.4）解振动的一些显示充分条件。

本文中，究竟下列具有欧拉形式的无界时滞中立型微分方程

为了推导出微分方程（1.6）解的振动准则，先给出其解以及解为振动的定义。

2 引理

引理2.1[11]设是区间上连续可导的正值函数，如果存在常数和使得对于充分大的成立，.

（2.2）

由（2.1），可得

（3）由（2）可知，

因此，引理证毕。

3 主要结论

在这一节，将应用前面的引理去建立方程（1.6）的所有解振动的一个充分必要条件，并由此出发，建立方程（1.6）的所有解振动的一此显示充分条件。

. （3.1）

必要性：反设方程（1.6）不是所有的解都振动，那么方程（1.6）至少存在一个非振动解。不妨假设是方程的一个最终正解，最终负解时的证明相似，故略. 令

由引理2.3，则最终有

再令

（3.3）

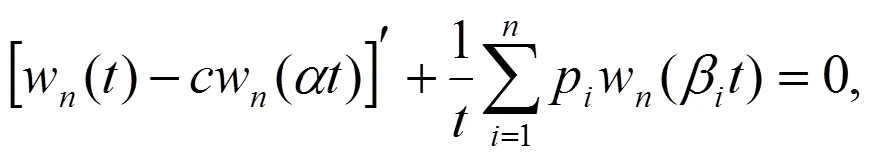
， （3.5）

和

定义集合

.

由（3.4）和（3.6）可得

或者

此表明

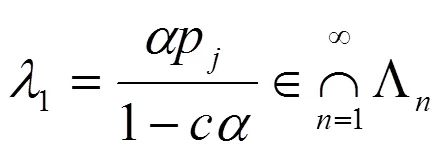
由引理2.1和引理2.2，有

注3.2 在文[10]中，作者研究了非中立型方程（1.4）解的振动性，得到该方程的所有解振动的充分必要条件（1.5）。因此，上述定理3.1将[10]中的结论推广到了中立型微分方程（1.6）.

定理3.3设

， （3.8）

那么方程（1.6）的所有解都振动。

证明：（3.1）等价于

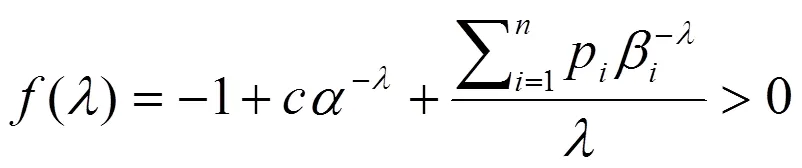
根据定理3.1 ,只须证明当（3.8）成立时，有（3.9）成立即可. 令

那么方程（1.6）的所有解都振动。因此，条件（3.8）改进了（3.10）。

那么方程（1.6）的所有解都振动。

因此

因此有（3.9）成立，利用定理3.1得方程（1.6）的所有解都振动. 定理证毕。

4 例子

下面举例说明定理的应用。考虑一阶中立型时滞微分方程：

考虑一阶中立型时滞微分方程

通过计算，发现定理3.5的所有条件是满足的。因此方程（4.2）的所有解都振动。

[1] Erbe,L.H., Q.K. Kong and B.G. Zhang. Oscillation Theory of Functional Differential Equations [M].Oxford: Clarendon Press, 1991.

[2] GyI. and G. Ladas. Oscillation Theory of Delay Differential Equations with Applications [M].Oxford: Clarendon Press, 1991.

[3] Kulenovic, M.R.S., G. Ladas and A. Meimaridou. Necessary and sufficient condition for oscillation of neutraldifferential equation [J]. J. Austral. Math. Soc. Ser. B, 28(1987):362-375.

[4] Zhang, B.G. Oscillation of first order neutral functional differential equatons [J]. J. Math. Anal. Appl., 139 (1989):311-318.

[5] Jiang, Z.W. Oscillation of first order neutral differential equations [J]. J. Math. Anal.Appl., 196 (1995) :800-813.

[7] Das, P. Oscillation criteria for odd order neutral equations [J]. J. Math. Anal. Appl.,188(1994) :245-257.

[8] Wang, Q.R.Oscillation criteria for first-order neutral differential equations [J]. Appl. Math. Lett.,15 (2002):1025-1033.

[9] Berezansky, L. and E. Braverman. Oscillation criteria for a linear neutral differential equations [J].J. Math. Anal. Appl., 286}(2003) :601-617.

[10] Dahiya, R.S. and T. Candan. Oscillation behavior of arbitrary order neutral differential equations [J]. Appl. Math. Lett., 17 (2004):953-958.

[11] An Ran. Oscillation criteria of solutions for delay differential equations [J].Mathematics in Practice and Theory, 30(3) (2000):310-314.

[12] Guan, K.Z. and J.H. Shen. Oscillation of first order neutral differential equations of Euler form [J]. Analysis, 27(2007):61-7

Oscillation of First-order Neutral Differential Equation of EulerType with Unbounded Delays

WANG Yuan1, SHEN Jianhua2

(1. Institute of Mathematics and Physics, Central South University of Forestry and Technology, Changsha 410004, Hunan, China; 2. Institute of Mathematics and Physics, Hangzhou Normal University, Hangzhou310036, Zhejiang, China)

We have researched the oscillation of solution of first order neutral differential equation of Euler type, which is with unbounded delays in this paper. The existing references have only discussed the equation when c=0 and n=1, but in practice, a lot of problems don't meet this condition. To break the limitation, we extent the equation to n. At first, we introduce its characteristic equation and establish a sufficient and necessary condition for the oscillation of all solutions of the equation. Then some explicit oscillation results are presented. This result is an extension of the existing works, which is significant in both theory and practice.

oscillation; neutral equation; unbounded delay; Euler type.

1672-9129(2016)01-00016-06

O175

A

2016-05-06；

2016-05-24。

国家自然科学基金青年项目NO. 11201490。

王媛（1968-- ），女，湖南永州人，副教授，硕士研究生，研究方向：常微分方程；申建华（1961-- ），男，教授，博士研究生，研究方向：常微分方程。