在空间相关Rice信道下的一种基于非码本的预编码方法在LTE下行系统中的应用

谢文武，刘守印

（1.华中师范大学物理科学与技术学院，湖北武汉430079；2.上海晨思电子科技有限公司，上海201210）

在空间相关Rice信道下的一种基于非码本的预编码方法在LTE下行系统中的应用

谢文武1，2，刘守印1

（1.华中师范大学物理科学与技术学院，湖北武汉430079；2.上海晨思电子科技有限公司，上海201210）

本文所提出的预编码生成方法适合在TD-LTE系统中工作，包括基于信道互易性获取信道状态信息模块，能量分配模块，波束形成模块.该方法充分利用了TDD系统的信道互易性特性，获取下行信道的信道状态信息，并使用基于非码本的预编码方式来增强传输的抗干扰性能，提升小区覆盖范围.与单纯考虑无视距LOS（Line-Of-Sight）分量的衰落信道不同，本文所提出的是在接收端天线之间存在空间相关的下行MIMO系统中，针对拥有LOS分量的莱斯（Rice）信道发射机的预编码设计方案.该方案可以保证非码本预编码算法的快速收敛，且保持较低的计算复杂度.

预编码；LTE；相关Rice信道；非码本

1 引言

长期演进（Long Term Evolution，LTE）系统是基于正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）和多入多出（Multiple-Input Multiple-Output，MIMO）技术的新一代宽带无线通信系统.在LTE物理层定义的传输模式（Transmission Mode，TM）2中，在发送端对于相邻频率子带使用了空频分组码（Space Frequency Block Code，SFBC）获取分集增益并增加链路可靠性［1，2］.同空时编码（Space-Time Block Code，STBC）相比，对于LTE标准提出的高速运动场景，SFBC系统的链路可靠性更高.而随着MIMO技术研究的进一步深入，在信道状态信息（Channel State Information，CSI）可以度量的情况下，发送端通常还会进一步采用预编码技术.预编码技术大致可以分为线性预编码与非线性预编码两大类.对于线性预编码来说，迫零（Zero Forcing，ZF）算法和最小均方误差（Minimum Mean-Square Error，MMSE）算法是两个较为著名的算法；而对于非线性预编码来说，Costa提出的脏纸编码（Dirty Paper Coding，DPC）则是一种典型的非线性预编码算法［3］.由于DPC的复杂性太高以至于难以实际应用，THP（Tomlinson Harashima Precoding）预编码作为DPC的一种性能与复杂度折中的改良方案［4，5］被提出.此外，预编码技术也可以分为基于码本和非码本的预编码方式.因为大多数预编码方案的发送端需要知道当前的信道状态信息，但是由于反馈信道的开销十分昂贵［6］，基于码本的预编码方法在这样的背景下被提出.基于码本的预编码方法使反馈信道所需传输的数据量较小，一般只需要几个比特，大大地减少了成本.基于非码本的预编码方式比较常见的有：基于线性接收机的奇异值分解（SVD）算法、基于迫零串行干扰消除（Zero Forcing-Successive Interference Cancellation，ZF-SIC）接收机的几何均值分解（GMD）算法［7，8］，以及在GMD基础上改进的统一信道分解（UCD）算法［9］等.还有基于上述方案的改进版本，如双码本的MIMO预编码［10］、基于最大 SNR的多用户MIMO预编码［11］等方案.

在TDD系统中，由于上下行传输采用相同的频带，可以利用信道互易性，在基站端通过估计上行的信道，来获得下行的信道信息［12］.因此TDD系统中基于非码本的预编码技术成为可能.本文假设上下行信道之间的互易性是理想的，即通过互易性获得的信道与下行真实的信道之间存在的误差可以忽略，但是在仿真阶段，还是针对估计误差对性能的影响进行了简单的仿真与分析.此时，采用非码本的预编码技术能够有效的抑制干扰，提高系统的性能.

3GPP采用空间信道模型（Spatial Channel Model，SCM）描述MIMO系统的衰落信道［13］.实际上，SCM的衰落可以被抽象为一个具有非零均值的空间相关的莱斯信道，这是因为基站在蜂窝内与接收机之间可能会存在视线分量（Line of Sight，LOS）.当LOS均值为零时，上述信道可退化为传统的瑞利衰落信道.因此，本文的方法针对更为通用的莱斯信道模型.通常，利用信道均值与空间相关的知识作为 CSI，线性的预编码器可进一步改善LTE系统的分集增益.现有文献提出的关于莱斯信道的预编码方案存在如下问题：简化操作使分集性能降低［14］；需要很高的计算复杂度且算法的收敛性不能保证［15］.本文提出了一种以最小化字符差错率（Symbol Error Rate，SER）上界作为优化准则的非码本预编码设计方案，可以在降低复杂度的同时保证算法的收敛.该方法可被应用于LTE系统传输模式 TM2或其他传输模式的备选传输方式中，用于提高蜂窝小区边缘的覆盖能力并增强传输可靠性.

2 信号模型

本文考虑的MIMO系统装配了Nt条发射天线和Nr条接收天线，并假定该系统有Nsub个子载波数，第k个子带上的承载信息为 ck，而在进行信息数据发送之前，使用一个线性预编码矩阵F进行预编码操作.假设在发送一个SFBC码字所经历的频带范围内，MIMO信道矩阵不发生变化.则接收信号可以表示为：

其中ρ表示总的发送信号能量与噪声的比率（SNR）；n 是Nr×Nf的噪声矩阵，噪声矩阵中每个元素服从高斯随机分布 CN（0，1），其中Nf≤Nsub表示码字的字长；C 在LTE协议里面给出了明确定义［1］；Y表示所有子带的接收信号，表示为，其 中yk表示第k个子带上接收端信号，并可以表示为yk=

衰减信道频率响应H可以被看成由两部分组成［13］：确定性的LOS分量和随机的多径衰落分量.具有空间相关的莱斯信道频率响应矩阵可以等效表示为［16］

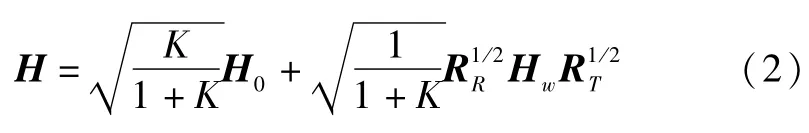
其中K表示莱斯信道的K因子；Hw是一个矩阵元素具有CN（0，I）高斯随机矩阵；H0表示确定性的归一化的信道均值且和RT分别表示接收与发送端空间相关矩阵.为简化分析，定义；并将H进行向量化操作，即h= vec（HH），h表示一个循环对称的高斯随机变量矢量，并且服从均值为、协方差矩阵为RR⊗INt分布，则h的概率密度函数［17］可以表示为ph（h）

3 预编码方案

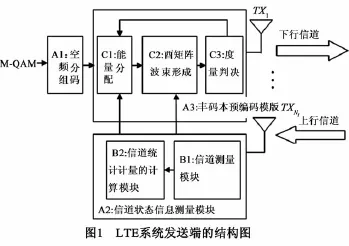
在LTE中发射端的结构图如图1所示，发送信号在经过调制和SFBC编码之后，根据TDD系统信道互易性得到UE端的信道均值¯H和相关矩阵RR等信道统计信息，估计最优的预编码矩阵 F.对于 F的估计包括两部分的内容：能量分配策略与确定波束形成方向.与传统的针对瑞利信道的基于特征值分解（Eigenvalue Decomposition，EVD）的非码本预编码不同，此处能量分配与波束形成方向因为¯H的存在而无法简单求解获得.

在TDD系统下，假定信道互易性是理想的，则接收端已知CSI，于是使用最大似然（ML）方法进行SFBC的解码.为了方便分析，本文采用正交SFBC［18］降低解码复杂度，则在上面假定的前提下，系统的SER的Chernoff上界［19］可表示为

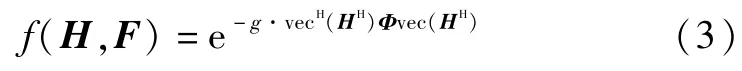
为了求解出最小化f（F）的预编码矩阵，需要对等式（4）进行进一步简化.依据特征值分解，等式（4）可以写成［17］

接着对f（F）做对数运算并删除掉和预编码矩阵F无关的项，此预编码的优化设计便可转化为一个带有归一化能量约束的求最大值的问题，即

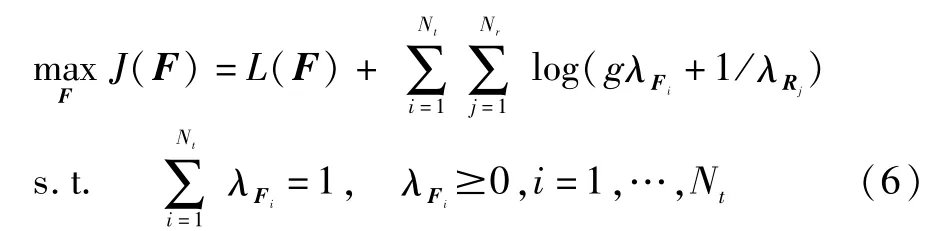
其中与信道均值¯h有关的项为

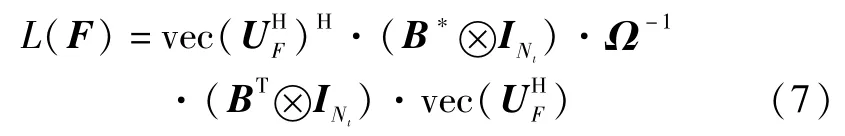
其中［·］*和［·］T分别表示共轭和转置操作；B=，其中根据 J（F）和L（F）的对比可以发现，UF只与L（F）有关，且无法通过简单的EVD分解确定预编码矩阵.可见，对J（F）求解最大值是一个非线性的优化问题，可以通过非线性规划（nonlinear programming）的方式加以解决.另外为了降低计算的复杂度，采用分步求解的方法，即分别求解非码书预编码矩阵的特征值矩阵ΛF（能量分配）和特征向量矩阵UF（波束形成方向）.

4 能量分配模块

将UF代入到L（F）中，则等式（7）将变成一个只与能量分配λF有关的函数，即

经推导，J（λF）关于λFi的二阶导数为

其中

由式（9）可见，J（λF）关于λFi的二阶偏导数总为负，这表明J（λF）是一个关于λFi的凹函数.又因为等式约束为线性的，所以上述优化问题是一个最大化凹函数的凸优化问题.于是，λFi可以使用内点法来求解最优值.一旦获得了最优的λFi便可以将其带如酉矩阵波束形成模块优化UF.

首先，假设ΛF固定，于是只以UF为变量的优化问题可简化为

等式（10）中的约束条件可以分别等价于如下N2t个多项式等式

其中m=1，…，Nt；n=m+1，…，Nt；Re（·）和Im（·）分别用来表示复数的实部和虚部；vFm表示UHF的第m 列.接下来定义两个Hermitian矩阵

其中，

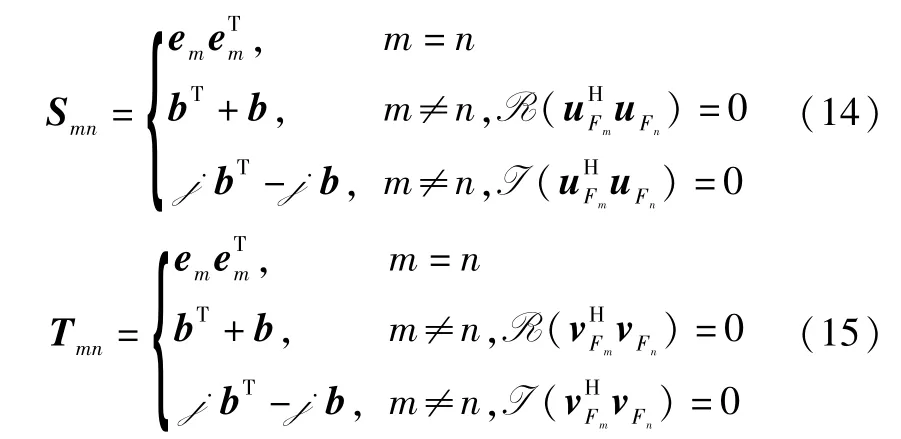
其中j「=-1，b=eneTm，并且em表示第m个单位向量.上述优化问题中的两个酉矩阵约束条件分别满足下述条件

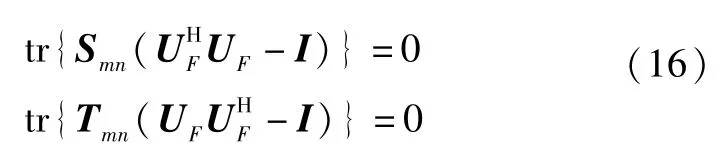
综上各式，进一步定义下述矩阵

在经过一系列的化简之后，上述优化问题中两个酉矩阵约束可以化为下面的实数集映射

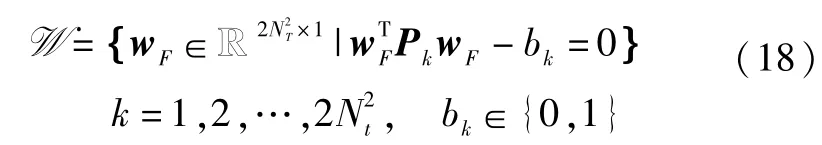
即上述酉矩阵约束转化为2N2t个二次型等式，例如此时，优化问题（最大化L（UF））可以被重写为

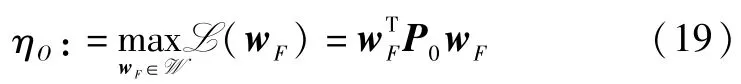
上述问题是一个以wF为自变量的具有二次型约束的二次型优化问题（Quadratic Constrained Quadratic Problem，QCQP）.该问题并不是凸优化问题（convex problem），所以难以求解.基于主函数和对偶函数的对应关系，可以考虑用拉格朗日对偶松弛（Langrangian dual relaxation）方法求解.上述优化问题（最大化L（wF））的Lagrangian形式可以表示为

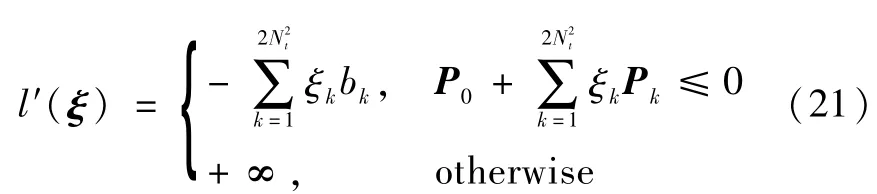
其中矩阵P≤0代表P为非正定矩阵.上述推导使用了显而易见的概念：二次型的上确界要么是0（如果二次型的矩阵非正定），要么是 +∞（如果二次型的矩阵是半正定的）.

显然，l′（ξ）≥ηO总是可以满足，于是利用Lagrangian dual function寻找最佳的上界，即求解最大化L（UF）的对偶问题（dual problem）

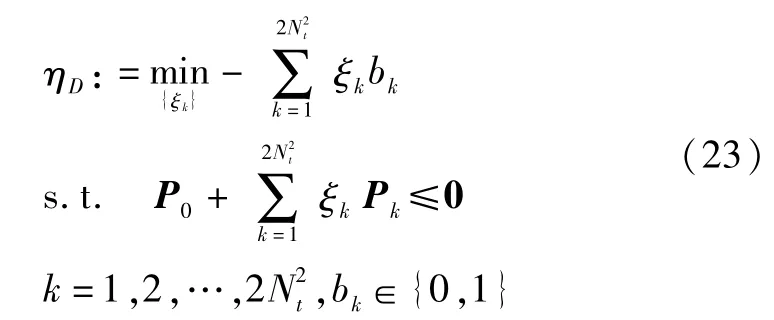
此时，上述问题可以被看做是一个半正定规划（Semi-Definite Programming，SDP）问题，更精确的说是一个以拉格朗日乘子为自变量的线性矩阵不等式LMI（Linear Matrix Inequalities）问题.该LMI问题可以通过LMI优化工具箱求解.

在得到最优拉格朗日乘子ξ*之后，根据KKT条件，便可利用主问题求解模块求解wF，然后再利用优化问题的映射模块进行UF的求解.

5 仿真

为了验证本文方案的性能，本章节在3×3与4×4 的MIMO配置下，分别与文献［14，15］进行了性能对比，如图2和图3.仿真结果显示，在3×3的配置环境下，本文方案在高 SNR情况下比文献［15］性能优1.5dB@SER 0.001%，与文献［14］性能相当，但是本文方案的复杂度更低.在4×4的配置环境下，在高SNR情况下比文献［14，15］性能均优.

为了评估非理想CSI对性能的影响，本文用仿真的性能对其进行了衡量，仿真结果如图4所示.由图中可以看出，在低SNR情况下，对性能影响较大；而在高SNR情况下，影响越来越小，这是因为 CSI的估计在高SNR情况下估计越来越精确的缘故.

6 结论

本文提出的一种以最小化SER上界作为优化准则的非码本预编码设计方案，可以在降低复杂度的同时保证算法的收敛.该方法可被应用于LTE系统传输模式TM2或其他传输模式的备选传输方式中，用于提高蜂窝小区边缘的覆盖能力并增强传输可靠性.本文要解决的问题是：考虑在TDD信道互易性状况下，如何充分利用信道均值和空间相关信息进行下行MIMO系统预编码设计，以提高基于非码本的预编码设计方案.

［1］3GPP TS 36.211，Evolved Universal Terrestrial Radio Access（E-UTRA）；Physical Channels and Modulation［S］. ［2］3GPP TS 36.101，Evolved Universal Terrestrial Radio Access（E-UTRA）；User Equipment（UE）Radio Transmission and Reception［S］.

［3］Costa MHM.Writing on dirty paper［J］.IEEE Transactions on Information Theory，1983，29（3）：439-441.

［4］Tomlinson M.New automatic equalizer employing modulo arithmetic［J］.Electronics Letters，1971，7（5）：138-139.

［5］Harashima H，Miyakawa H.Matched-transmission technique for channels with intersymbol interference［J］.IEEE Transactions on Communications，1972，20（4）：774 -780.

［6］Wang Shu，Kim Hobin.On the feedback channel for MIMO beamforming［A］.Proceedings of Wireless Communications and Networking Conference［C］.USA：IEEE，2008. 683-687.

［7］Jiang Y，Hager W W.The geometric mean decomposition ［J］.Linear Algebra and Its Applications，2005，396（1）：373-384.

［8］Jiang Yi，Li Jiang.Joint transceiver design for MIMO communications using geometric mean decomposition［J］. IEEE Transactions on Signal Processing，2005，53（10）：3791-3803.

［9］Jiang Y，Li J.Uniform channel decomposition for MIMO communications［J］.IEEE Transactions on Signal Processing，2005，53（11）：4283-4294.

［10］刘建国，杨绿溪.有限反馈MIMO系统中一种基于双码本的功率分配与预编码方案［J］.电子学报，2007，35 （6A）：78-82. Liu Jian-guo，Yang Lü-xi.Precoding and power allocation based on double codebook in MIMO systems with limited feedback［J］.Acta Electronica Sinica，2007，35（6A）：78 -82.（in Chinese）

［11］唐万斌，李少谦.基于最大化信干噪比的多用户MIMO下行预编码［J］.电子学报，2007，35（6A）：157-160. Tang Wan-bin，Li Shao-qian.Linear precoding based on maximum SJNR in multi-user MIMO downlink［J］.Acta Electronica Sinica，2007，35（6A）：157-160.（in Chinese）

［12］Roh J C，Rao B D.Multiple antenna channels with partial channel state information at the transmitter［J］.IEEE Transactions on Wireless Communications，2004，3（2）：677-688.

［13］3GPP TR 125.996，Universal Terrestrial Radio Access （UTRA）；Spatial Channel Model for Multiple Input Multiple Output（MIMO）Simulations［S］.

［14］L Zhang，Z Luo，et al.Simplified precoder design for MIMO systems with receive correlation in Ricean channels ［J］.IEEE Signal Processing Letters，2012，19（5）：263 -266.

［15］A Hjorungnes，D Gesbert.Precoded orthogonal space-time block codes over correlated Ricean MIMO channels［J］. IEEE Transactions on Signal Processing，2007，55（2）：779 -783.

［16］John G Proakis，Massoud Salehi.Digital Communications （5th Edition）［M］.USA：McGraw Hill Higher Education，2008.

［17］张贤达.矩阵分析与应用（第二版）［M］.北京：清华大学出版社，2004. Zhang Xianda.Matrix Analysis and Application（2nd Edition）［M］.Beijing：Tsinghua University Press，2004.（in Chinese）

［18］V Tarokh，H Jafarkhani，A Calderbank.Space-time block codes from orthogonal designs［J］.IEEE Transactions on Information Theory，1999，45（5）：1456-1467.

［19］M Fozunbal，et al.On space-time-frequency coding over MIMO-OFDM systems［J］.IEEE Transactions on Wireless Communications，2005，4（1）：320-331.

谢文武 男，湖北荆州人.2004年、2007年分别在华中师范大学获学士和硕士学位.现为华中师范大学物理学院在读博士生，并在上海晨思电子科技有限公司信号处理部门任经理一职，主要从事无线通信算法相关领域研究工作.

E-mail：xiewenwu123@sohu.com

刘守印 男，河南郸城县人.现为华中师范大学物理科学与技术学院教授.主要从事无线通信理论、物联网等领域的研究.先后获湖北省科学技术进步奖，武汉市科技发明奖，韩国政府邀请外国留学生“学术研究奖”等多项荣誉.

E-mail：syliu@phy.ccnu.edu.cn

The Application of a Precoding Method Based on Non-Codebook in LTE Downlink Under Spatial Correlated Rice Channel

XIE Wen-wu1，2，LIU Shou-yin1
（1.College of Physical Science and Technology，Central China Normal University，Wuhan，Hubei 430079，China；2.Shanghai Chensi Electronic and Technology Co.，Ltd.，Shanghai 201210，China）

This paper proposed a method to generate precoding，which is applicable to the TD-LTE system.This method contains three parts：channel state information（CSI）model，energy distribute model，and beam-forming model.This scheme fully uses the character of exchanging channel for the TDD system，which can obtain the CSI of the downlink channel，and enhances the performance of anti-interference by using the precoding based on the non-codebook.Furthermore，it can enlarge the range of the serving cell.The background of this paper is LTE downlink system equipped with these spatial-correlated receive antennas，where a transmitted precoding method is designed for Rice channel with LOS.This method can keep the precoding algorithm based on non-codebook at a quick convergence speed with low calculation complexity.

precoding；LTE；correlated rice channel；non-codebook

TN911

A

0372-2112（2016）04-0983-05

电子学报URL：http：//www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.04.032

2014-12-01；

2015-06-24；责任编辑：孙瑶