基于分数阶四元数傅里叶变换的彩色图像自适应水印算法
2016-10-13王金伟周春飞王水平陈北京孙星明
王金伟 周春飞 王水平 陈北京 孙星明
基于分数阶四元数傅里叶变换的彩色图像自适应水印算法
王金伟①②周春飞①王水平①②陈北京*①②孙星明①②
①(南京信息工程大学计算机与软件学院 南京 210044)②(南京信息工程大学江苏省网络监控工程中心 南京 210044)
针对现有一些彩色图像自适应水印算法在自适应过程中未充分考虑色彩信息或者在嵌入过程中未考虑彩色载体图像分量的整体性等不足,该文提出一种基于分数阶四元数傅里叶变换(FrQFT)的彩色图像自适应数字水印算法。首先利用人类视觉系统(HVS)提取彩色载体图像块的纹理、边缘和色调掩蔽特性,并依据这些特性对适合嵌入图像块自适应分配嵌入强度,然后在FrQFT域以自适应强度采用量化索引调制算法和冗余嵌入策略嵌入水印。实验结果表明,该算法优于现有的基于四元数傅里叶变换(QFT)的算法以及基于分数阶傅里叶变换(FrFT)的算法,具有较好的不可见性和鲁棒性。
彩色图像;自适应水印;四元数;分数阶傅里叶变换
1 引言
数字水印技术是把某些特定的数字信息(即数字水印),通过嵌入算法将其内嵌到数字载体中,由此可以用于确定数字产品的拥有者、传递秘密信息或判断数字内容是否被篡改等,从而实现版权的保护[1]。对于数字图像水印,当前很大部分算法仍然是针对灰度图像。相对少量的针对彩色图像的水印算法大致可以分为3类:灰度化方法[2]、三通道分别处理方法[3]与基于四元数的方法。基于四元数的方法将彩色图像采用纯四元数表示(详见2.1节),然后在四元数空间域或变换域嵌入水印。相对于灰度化方法,基于四元数的方法因为考虑了所有彩色分量,大大增加了水印容量;相对于三通道分别处理方法,基于四元数的方法因为采用了基于四元数的彩色图像表示方法,从而考虑了彩色图像三分量的整体性及其相关性。因此,本文将采用基于四元数的方法。
从信号处理角度看,嵌入水印可以看成是在强信号(即载体图像)上叠加弱信号(即水印图像),只要叠加的信号小于恰可察觉性失真的值,人类视觉系统(Human Vision System, HVS)就无法感受到水印的存在。因此,应该充分利用HVS的视觉特点,在保证含水印图像视觉质量的前提下,自适应的分配嵌入水印的强度,充分提高水印的鲁棒性。当前的彩色图像自适应水印算法考虑的掩蔽特征大部分都是基于灰度化图像提取。比如在唯一公开发表的基于四元数的工作中,江淑红等人[4]就是考虑了灰度化后的彩色载体图像的纹理、边缘和亮度特征,然后在彩色载体图像的四元数傅里叶变换(Quaternion Fourier Transform, QFT)域自适应嵌入水印。这些算法的不足之一在于自适应过程未充分考虑彩色信息。因此,本文的自适应算法将直接在彩色载体上提取纹理、边缘和色调掩蔽特性。
现有水印算法按嵌入域分大致可分为两大类:空域算法和频域算法。相比于空域算法,频域算法具有更强的鲁棒性。因此,很多变换都已成功应用于数字水印领域,常见的包括离散傅里叶变换[7],离散小波变换[8],分数阶傅里叶变换[9]等。本文将基于分数阶四元数傅里叶变换(Fractional Quaternion Fourier Transform, FrQFT)[10]提出一种自适应水印算法。采用的FrQFT是分数阶傅里叶变换[11](Fractional Fourier Transform, FrFT)在四元数域上的扩展,是一种广义的QFT。FrQFT作为一种分数阶变换,随着阶数从0连续增长到1,可以展示出信号从时域逐步变化到频域的所有特征[11],而且还多了一个自由参数(变换阶数),这有利于增强水印算法的安全性。
2 分数阶四元数傅里叶变换
2.1四元数及彩色图像四元数表示
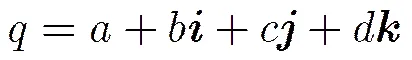
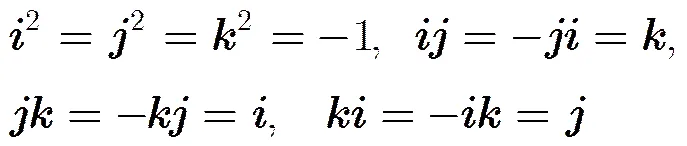
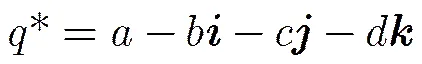
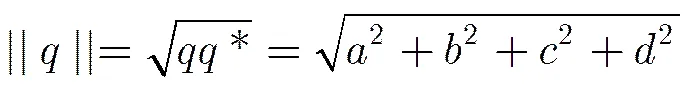
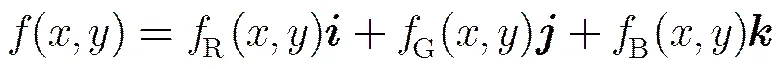
2.2 分数阶四元数傅里叶变换
Xu等人[10]于2008年提出了FrQFT。对于四元数信号,其阶的FrQFT定义为
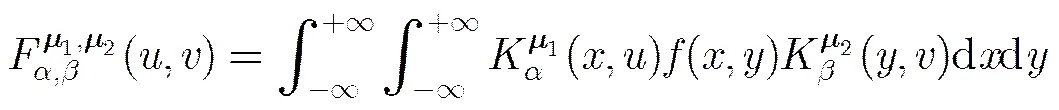
3 彩色图像自适应水印掩蔽
针对当前彩色图像自适应水印算法在自适应过程未充分考虑色彩信息的不足,本文将直接在彩色载体上提取每个块的纹理、边缘和色调3个不同特性,依据这3个特性自适应调节水印嵌入强度。接下来对不同掩蔽特性的提取进行详细解释。
3.1 纹理掩蔽
由于HVS对平滑区的噪声敏感度要高于纹理变化频繁的区域,所以对纹理比较丰富的图像块赋予较高的水印强度[4]。
文献[12]指出:局部方差反映了单个像素值与当前滑动窗内像素均值之间的关系,是判定当前区域是否是纹理丰富区的关键值。因此,该文定义像素点的纹理度为
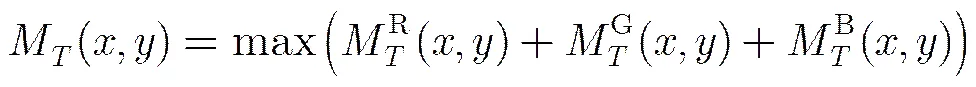
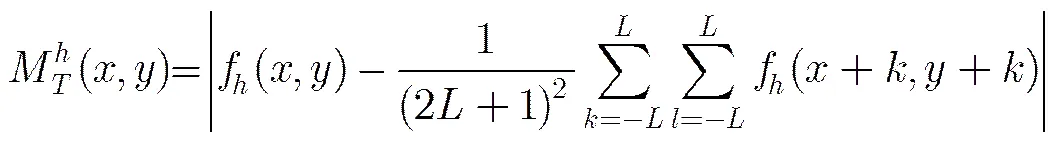
3.2边缘掩蔽
由于HVS对于边缘比较敏感,所以对边缘比较丰富的图像块赋予较小的水印强度[4]。
对于彩色图像来说,从其对应的灰度图像中并不能完全提取出彩色图像的边缘信息[13],彩色图像的边缘检测不仅要考虑图像的亮度变化,而且要考虑色度变化。本文采用文献[14]提出的基于四元数的彩色图像边缘度量方法:基于彩色图像四元数表示方法定义彩色图像的局部对比度函数,然后通过求解该函数的最大值作为边缘度量。该文定义像素点的边缘度量为
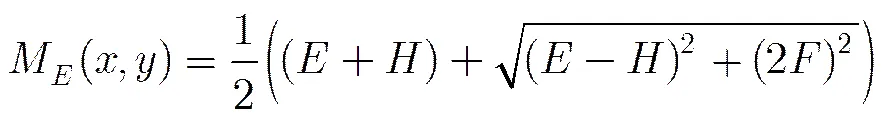
其中,
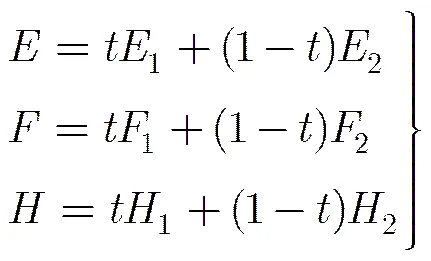
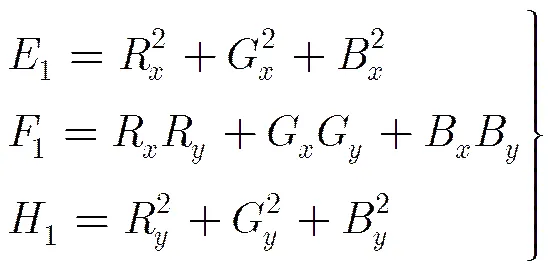
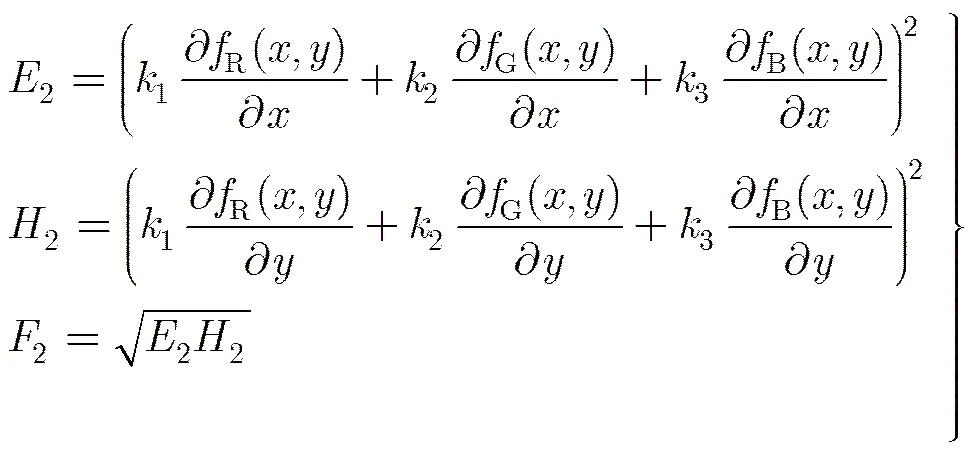
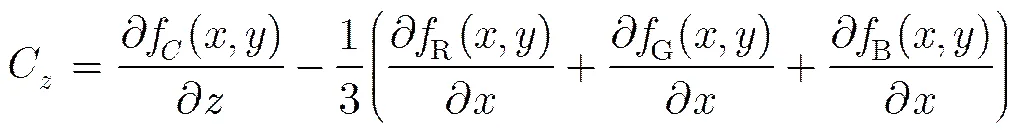
3.3色调掩蔽
彩色图像的一个重要属性就是色调,人眼对于暖色(如红色、黄色)的关注度显著高于冷色(如蓝色、绿色)[15],因此可对暖色图像块赋予较小的水印强度。
文献[16]指出:彩色图像CIEL***空间中的*通道包含绿-红信息,*通道包含蓝-黄信息。如果一个像素的*或者*值较高,那么这点看上去较“暖”,反之,则较“冷”。该文提出计算像素色调的算法如下:
(2)采用最大最小值法对*和*通道进行线性归一化,得到和。
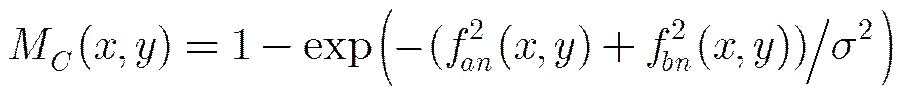
3.4综合自适应掩蔽因子
上述3小节已介绍了单个像素点的纹理、边缘和色调度量的计算。接下来介绍一个块3个度量的计算。
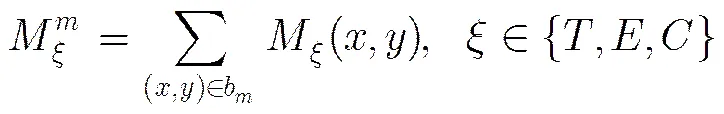
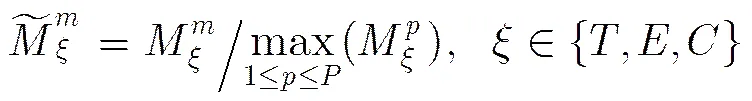
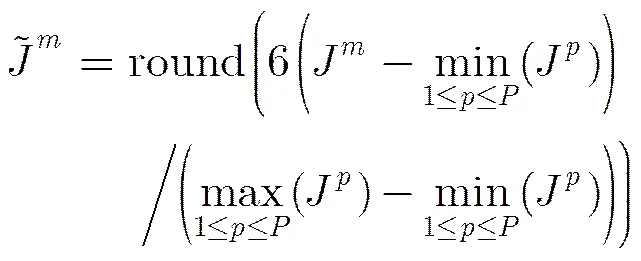
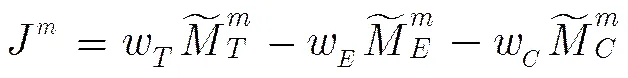
4 基于分数阶四元数傅里叶变换的水印算法
本文综合考虑第3节所介绍的彩色图像的纹理、边缘度和色调掩蔽特性,自适应的确定每个图像块的嵌入强度,在FrQFT域修改中频系数嵌入水印,具体算法流程图如图1所示。
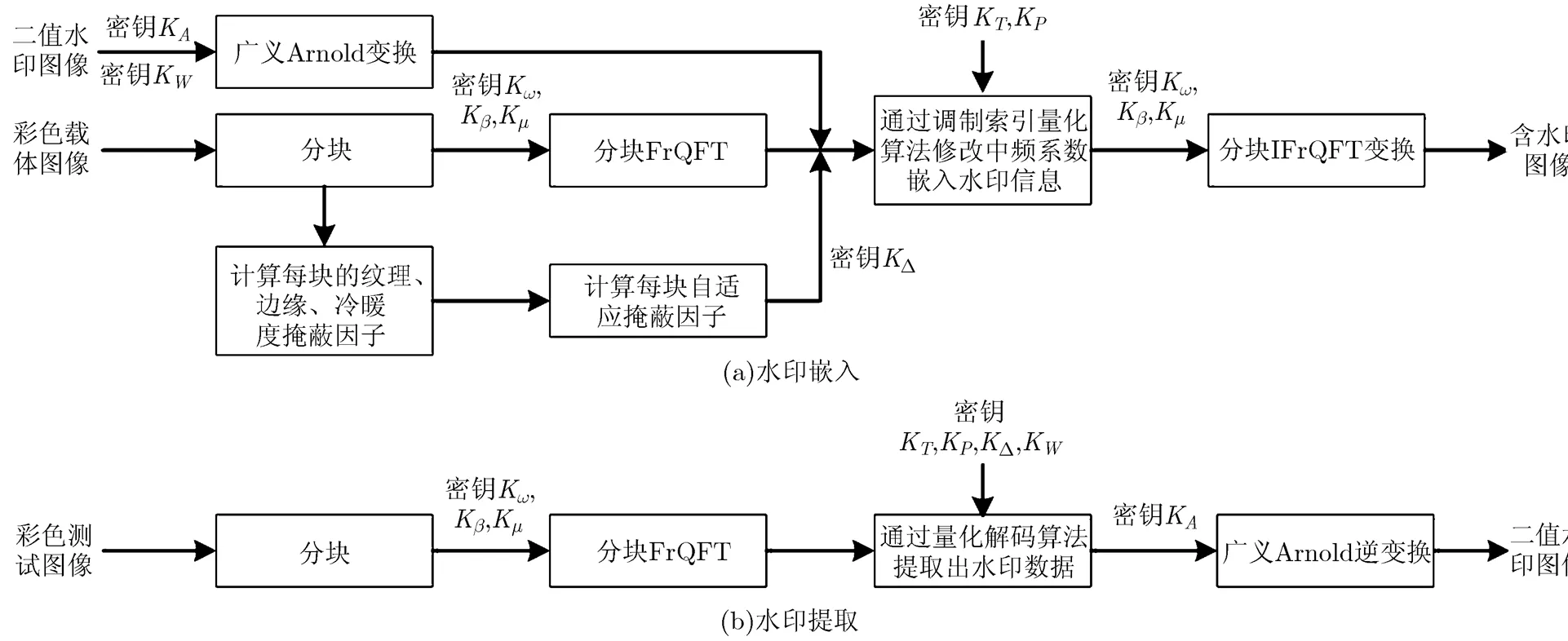
图1 彩色图像水印算法流程图
4.1嵌入水印前提条件
由式(5)可知,彩色图像是用纯四元数矩阵表示,其实部均为0。因此,在修改频域系数嵌入水印时必须保证修改后的系数在经过IFrQFT后得到的四元数的实部为0,否则,丢失非0的实部信息获取含水印图像可能导致提取水印失真。因此,接下来将分析讨论如何避免信息损失的问题。
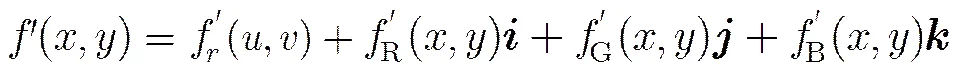
其中,
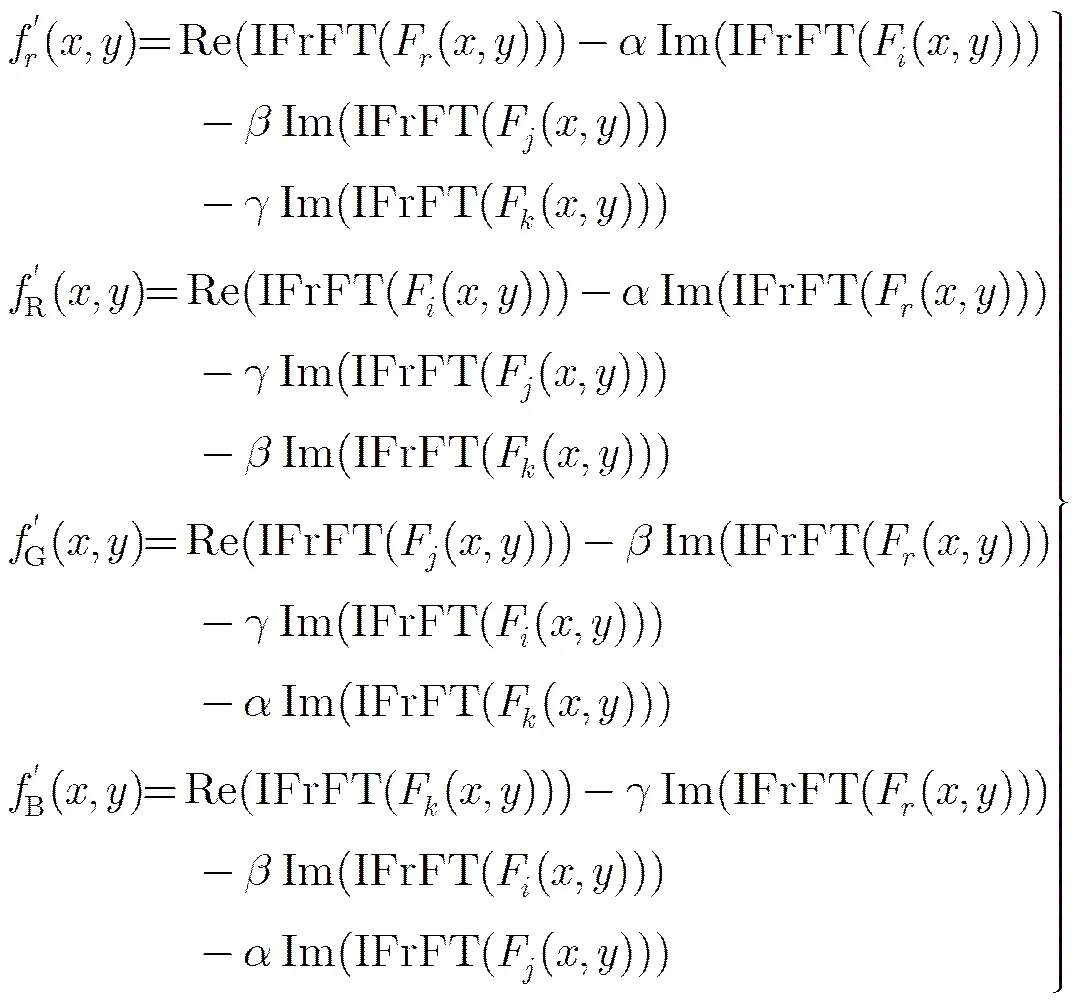
由式(21)可知,为了满足式(20)中的实部为0的前提条件,单位纯四元数不同,系数修改嵌入水印方案也不一样:(1)当,和均不为0时,修改系数后,式(20)实部通常情况下不为0,也就是说此时的单位纯四元数不适用于本文算法;(2)当,和有两个不为0时,此时可以修改,和中的一个分量,即式(21)第1个公式中参数为0所对应的分量;(3)当,和只有1个不为0时,此时可以修改,和中的两个分量,即式(21)第1个公式中参数为0所对应的分量。
4.2 水印嵌入
本算法的水印嵌入流程如图1(a)所示,具体过程
(1)水印图像预处理: 为了增强算法的安全性和抗裁剪攻击的鲁棒性,对水印图像进行广义Arnold变换。将尺寸为的二值水印图像(记为密钥)按式(22)进行次周期为的广义Arnold置乱:
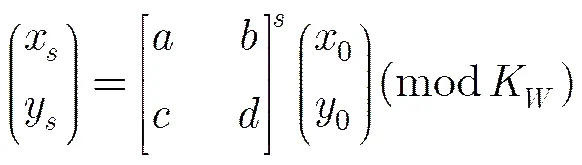
(2)分块FrQFT变换与自适应因子计算: 将彩色载体图像进行分块处理,每块大小为8×8。接下来,一方面对每个块进行阶数为单位纯四元数为的FrQFT(和作为密钥)得到彩色图像的FrQFT频域系数;另一方面,采用式(8),式(10)与式(15)分别计算纹理、边缘与色调掩蔽特性,然后采用式(18)计算每块的自适应因子(0~6级)。
(3)嵌入位置选择: 由于自适应因子为0的图像块相对来讲纹理更不丰富、边缘更丰富以及色彩更暖,因此这些块将不作为水印的嵌入块。对于其他图像块,将每个块的FrQFT系数按模值从大到小排序,考虑将水印嵌入到中间模值所对应的位置(嵌入位置作为密钥记为)。理由如下:如果在较小模值对应位置嵌入水印,则对图像压缩或滤波等攻击敏感,鲁棒性较差;如果在较大模值对应位置嵌入水印,则对载体图像造成较大的扰乱,不可见性较差。
(4)水印信息嵌入: 为了进一步增强算法的抗攻击鲁棒性,采用冗余嵌入策略,将置乱后的水印序列复制次得到新水印序列,并将其作为待嵌入信息。根据4.1节确定的针对单位纯四元数为的系数分量修改方案,对于式(3)中确定的嵌入位置,选择其对应变换系数的4个分量(,,,)中的一个或两个分量,然后将水印序列通过量化索引调制机制算法[5]平均嵌入到每个图像块:
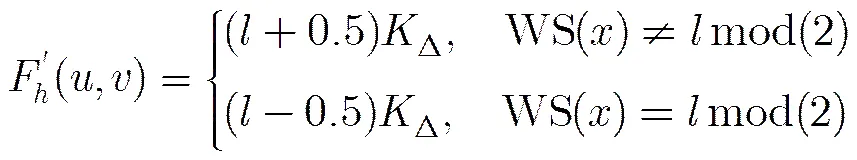
(5)含水印图像生成: 对所有的图像块进行分数阶四元数傅里叶逆变换(IFrQFT),得到含水印图像。
4.3 水印检测
本算法的水印检测流程如图1(b)所示,检测算法不需原载体图像参与,为盲检测。具体过程如下:
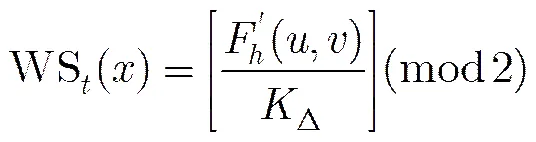
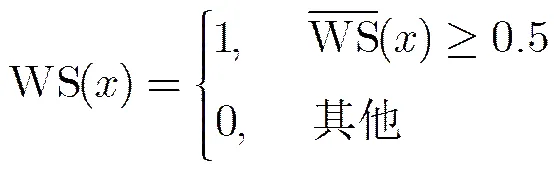
5 实验结果与分析
本节将从水印的不可见性和抗攻击的鲁棒性两方面验证本文算法的有效性。为了更好地展示算法效果,我们与基于FrFT的算法以及江淑红等人[4]提出的基于QFT的算法进行对比。基于FrFT的算法采用本文考虑的3个掩蔽因子自适应确定嵌入强度,然后在彩色图像每个分量的FrFT域嵌入水印。本文选取了6幅大小为512×512的经典标准彩色图像作为载体图像集,如图2(a)~图2(f)所示,2幅大小为64×64的Tmall和Volkswagen的二值logo图像作为水印图像,如图2(g)和图2(h)所示。在测试算法性能时,使用峰值信噪比PSNR[5]评估水印的不可见性,误比特率BER[8]评估水印的鲁棒性。
5.1 单位纯四元数及权值组合的选取
由4.1节可知,单位四元数不同,变换系数不同,修改系数嵌入水印的方案也不同,而由3.4节可知,式(19)中权值组合的不同,选择的嵌入块不同,嵌入强度也不同。因此,单位纯四元数与权值组合都将影响水印算法的性能。因此,我们对100个随机产生的单位纯四元数以及100组随机权值组合进行实验对比,比较不同单位纯四元数和不同权值组合下的算法获取的含水印图像与相应载体图像之间的PSNR值。100个单位纯四元数由随机选取的95个单位纯四元数以及常用5个([5],[5],[5],[5],[17])构成,100组权值组合由随机选取的99组权值组合和(1/3,1/3,1/3)[4]构成。算法其他参数设置:量化单位,分数阶,冗余嵌入次数,每块的具体嵌入位置考虑模值从大到小排序后的第7个位置开始。每个单位纯四元数针对图2中的所有6幅载体图像以及2幅水印图像获取的含水印图像的平均PSNR值如图3所示。由图3可知:(1)算法对于不同的权值组合的差异较大,最大标准差为1.8748,但对于不同的纯四元数的差异较小,最大标准差为0.2626,比较稳定;(2)效果最优的组合为第72个单位四元数0.6477+0.7619和第41个权值组合0.121, 0.056, 0.823构成,其PSNR均值为40.2922。接下来的实验本文算法就采用该最优单位纯四元数和权值组合。

图2 彩色载体图像集及二值水印图
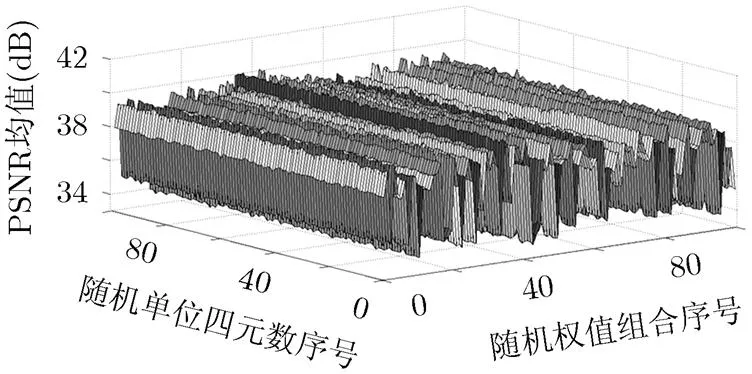
图3 100个单位纯四元数与100组权值组合针对所有载体图像和水印图像的平均PSNR值
5.2 不可见性测试
为了更好地进行不可见性对比实验,3种算法的参数设置基本一致(见5.1节),区别在于:基于QFT的算法[4]的单位纯四元数采用文献[4]中的,而本文算法采用5.1节得到的0.6477+ 0.7619。
表1显示了不同算法下不同载体图像嵌入不同水印图像得到的含水印图像与相应载体图像之间的PSNR值。表2则主要展示了载体图像图2(a)嵌入水印后得到的含水印图像及其在无攻击下提取的水印图像。从表1和表2可以看出,不管对于水印图像图2(g)还是图2(h),本文提出的基于FrQFT的算法优于对比的两种算法,具有较高的PSNR值,在无攻击的情况下能完全正确提取水印。主要原因在于:(1)本文提出算法直接对彩色图像提取自适应掩蔽因子,并将不适合嵌入水印的图像块剔除,而基于QFT的算法则是对灰度化后图像提取自适应掩蔽因子;(2)本文提出算法采用了基于四元数的彩色图像整体处理方案,并考虑了三通道之间的关联性,而基于FrFT的算法则对3个通道分别进行处理。

表1 不同算法下不同载体图像嵌入不同水印图像后PSNR值(注:载体图像集为均值)
5.3 鲁棒性测试
不失一般性,继续采用图2中的6幅载体图像以及2幅水印图像做测试。对含水印图像进行7种不同类型的攻击测试算法的鲁棒性。7种攻击分别为模板大小均为3×3的高斯滤波、中值滤波、均值滤波和运动模糊,质量因子为10~100(间隔为10)的JPEG压缩,均值为0方差为0.001~0.01(间隔为0.001)的高斯噪声,密度为0.2%~2%(间隔为0.2%)的椒盐噪声。
由于水印的不可见性和鲁棒性相互制约,为了保证对比的公平性,对于不同算法,首先通过调整量化单位使对比的两种算法所得到的含水印图像的PSNR值与本文算法在5.2节所得的结果接近,然后再对各含水印图像进行各种攻击实验。以载体图像图2(a)、水印图像图2(g)为例,得到的含水印图像的PSNR分别为:基于QFT的算法为40.5782 (此时),基于FrFT的算法为40.6235(此时),本文提出的基于FrQFT的算法为40.6353(此时)。
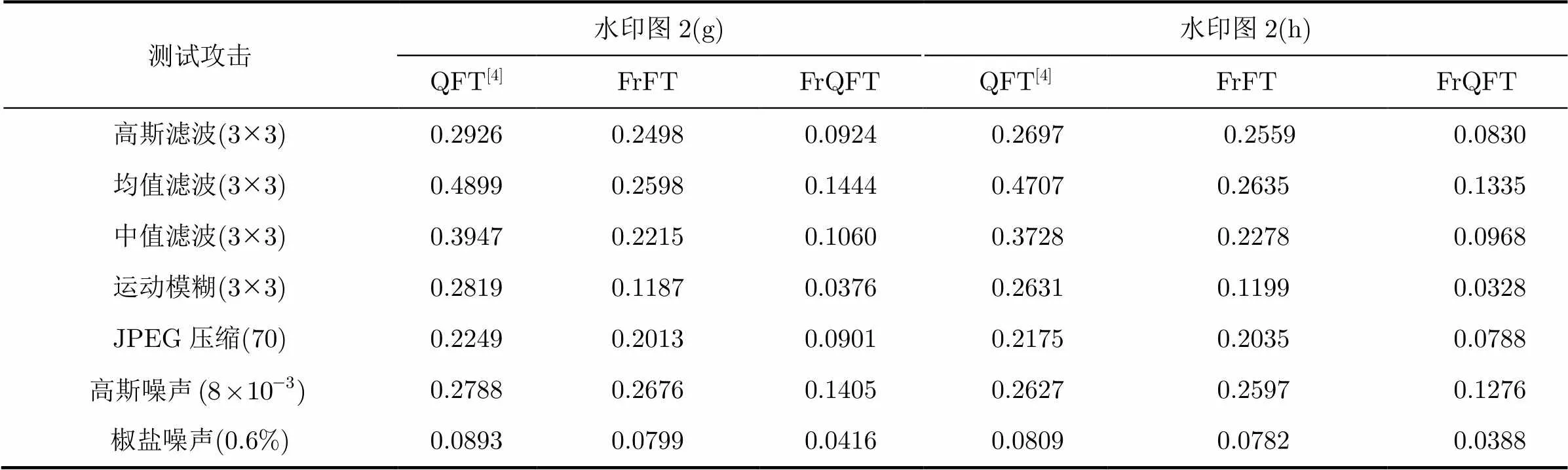
表3和图4给出了3种算法在载体图像图2(a)嵌入不同水印并遭受各种攻击后提取的水印结果。表4则展示了各算法对于整个载体图像集的结果。从这些结果可以看出:(1)对于考虑的不同程度的7种类型攻击,本文提出的基于FrQFT的算法的效果均优于两种对比算法,尤其是对于滤波攻击,各种滤波攻击下提取水印尽管有少许噪声但均易于识别,原因在于:本文算法一方面直接对彩色图像提取自适应掩蔽因子另一方面采用了基于四元数的彩色图像整体处理方案;(2)对于两种对比算法,基于FrFT的算法抗攻击性上在滤波攻击方面优于基于QFT的算法,但在JPEG压缩以及噪声攻击方面,当攻击强度较大时基于FrFT的算法优于基于QFT的算法但强度较小时则相反。
表2 不同算法下载体图像图2(a)嵌入不同水印图像后得到的含水印图像及其提取水印
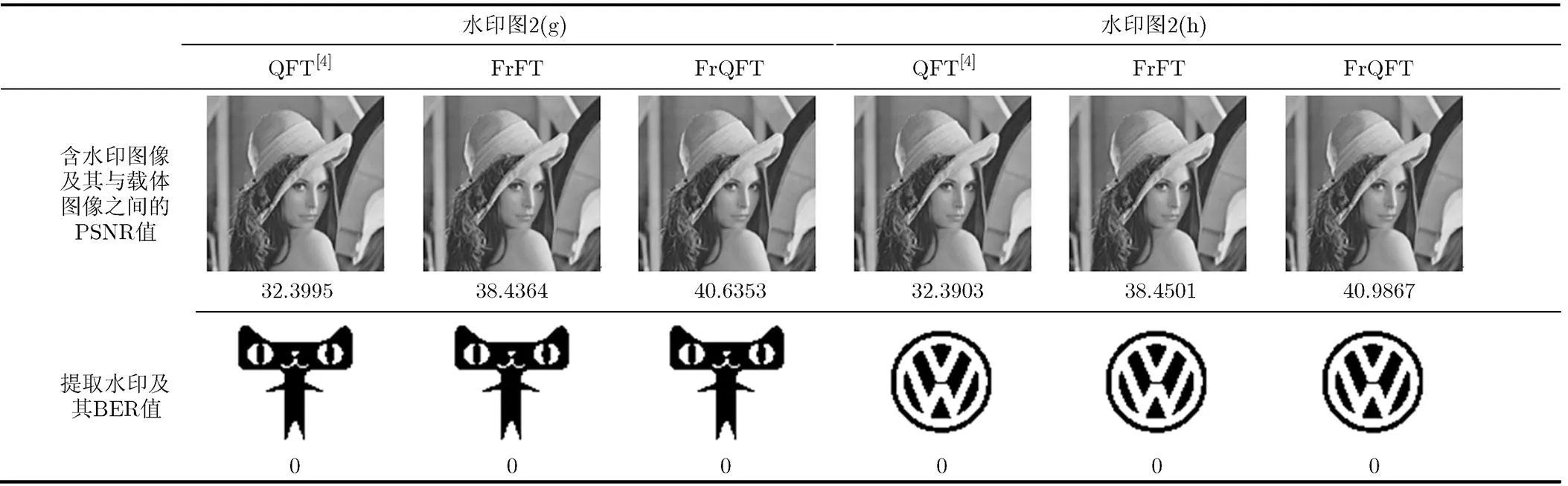
表3载体图像图2(a)嵌入不同水印并遭受滤波攻击后提取的水印及其BER值

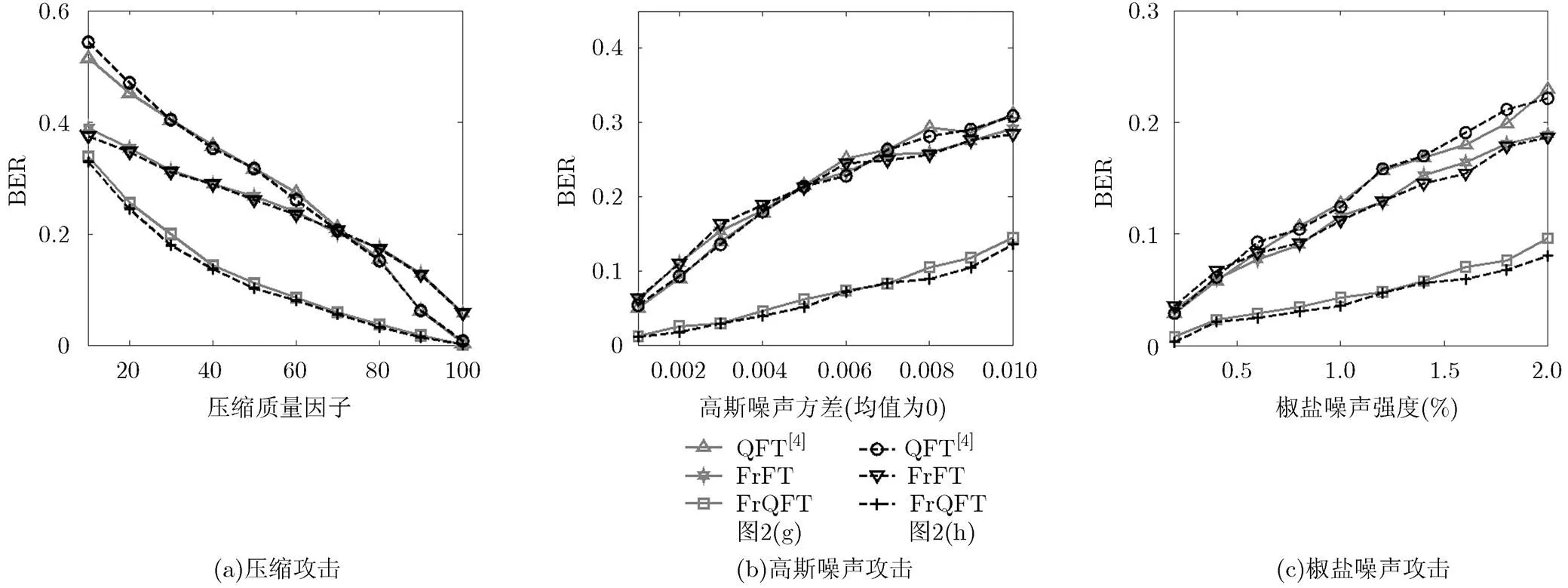
图4 载体图像图2(a)嵌入不同水印后在不同压缩和噪声攻击下提取水印的BER值
表4载体图像集嵌入不同水印后在不同攻击下提取水印的平均BER值
测试攻击水印图2(g)水印图2(h) QFT[4]FrFTFrQFTQFT[4]FrFTFrQFT 高斯滤波(3Í3)0.29260.24980.09240.26970.25590.0830 均值滤波(3Í3)0.48990.25980.14440.47070.26350.1335 中值滤波(3Í3)0.39470.22150.10600.37280.22780.0968 运动模糊(3Í3)0.28190.11870.03760.26310.11990.0328 JPEG压缩(70)0.22490.20130.09010.21750.20350.0788 高斯噪声0.27880.26760.14050.26270.25970.1276 椒盐噪声(0.6%)0.08930.07990.04160.08090.07820.0388
6 结束语
本文提出了一种基于FrQFT的彩色图像自适应水印算法。该算法直接对彩色图像综合考虑了其纹理、边缘和色调的掩蔽特性,自适应地确定水印嵌入强度,在FrQFT域嵌入水印。本文算法较好地平衡了不可见性和鲁棒性,相对于对比的基于QFT的算法以及基于FrFT的算法,对滤波、JPEG压缩和噪声等攻击具有更强的鲁棒性,尤其是滤波攻击。而且,FrQFT的阶数可作为额外的参数密钥,增强了水印系统的安全性。本文提出算法的不足在于对几何变换攻击不鲁棒,下一步将研究有效的方法解决该问题。
[1] HARTUNG F and KUTTER M. Multimedia watermarking techniques[J]., 1999, 87(7): 1079-1107. doi: 10.1109/5.771066.
[2] 王方, 林泓. 基于DCT变换的彩色图像数字水印嵌入算法研究[J]. 软件导刊, 2007, 7(13): 116-117.
WANG F and LIN H. Research on the watermark algorithm of color image based on DCT[J]., 2007, 7(13): 116-117.
[3] THABIT R and KHOO B E. A new robust lossless data hiding scheme and its application to color medical images[J]., 2015, 38: 77-94. doi: 10.1016/j.dsp. 2014.12.005.
[4] 江淑红, 张建秋, 胡波. 彩色图像超复数空间的自适应水印算法[J]. 电子学报, 2009, 37(8): 1773–1778. doi: 10.3321/j.issn: 0372-2112.2009.08.026.
JIANG S H, ZHANG J Q, and HU B. An adaptive watermarking algorithm in the hypercomplex space of a color image[J]., 2009, 37(8): 1773-1778. doi: 10.3321/j.issn:0372-2112.2009.08.026.
[5] CHEN B, COATRIEUX G, CHEN G,. Full 4-D quaternion discrete Fourier transform based watermarking for color images[J]., 2014, 28(5): 106-119. doi: 10.1016/j.dsp.2014.02.010.
[6] 孙菁, 杨静宇. 四元数域彩色图像整体式水印算法[J]. 电子与信息学报, 2012, 34(10): 2389-2395. doi: 10.3724/SP.J.1146. 2011.00789.
SUN J and YANG J Y. Quaternion based holistic color images watermarking algorithm[J].&, 2012, 34(10): 2389-2395. doi: 10.3724/SP.J.1146.2011.00789.
[7] URVOY M, GOUDIA D, and AUTRUSSEAU F. Perceptual DFT watermarking with improved detection and robustness to geometrical distortions[J]., 2014, 9(7): 1108-1119. doi: 10.1109/TIFS.2014.2322497.
[8] ALI M, AHN C W, PANT M,. An image watermarking scheme in wavelet domain with optimized compensation of singular value decomposition via artificial bee colony[J]., 2015, 301: 44-60. doi: 10.1016/j.ins. 2014.12.042.
[9] LANG J and ZHANG Z. Blind digital watermarking method in the fractional Fourier transform domain[J]., 2014, 53: 112-121. doi: 10.1016/ j.optlaseng.2013.08.021.
[10] XU G L, WANG X T, and XU X G. Fractional quaternion Fourier transform, convolution and correlation[J]., 2008, 88(10): 2511-2517. doi: 10.1016/j.sigpro. 2008.04.012.
[11] 陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用[M]. 北京:清华大学出版社, 2009, 1-47.
Tao R, Deng B, and Wang Y. Fractional Fourier Transform and Its Applications[M]. Beijing: Publisher of Tsinghua University, 2009: 1-47.
[12] QI H, ZHENG D, and ZHAO J. Human visual system based adaptive digital image watermarking[J]., 2008, 88(1): 174-188. doi: 10.1016/j.sigpro.2007.07.020.
[13] NOVAK C L and SHAFER S A. Color edge detection[C]. DARPA Image Understanding Workshop, Los Angeles, USA, 1987: 35-37.
[14] JIN L, SONG E, LI L,. A quaternion gradient operator for color image edge detection[C]. IEEE International Conference on Image Processing, Melbourne, Australia, 2013: 3040-3044. doi: 10.1109/ICIP.2013.6738626.
[15] SHEN X and WU Y. A unified approach to salient object detection via low rank matrix recovery[C]. IEEE International Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 2012: 853-860. doi: 10.1109/CVPR.2012.6247758.
[16] ZHANG L, GU Z, and LI H. SDSP: a novel saliency detection method by combining simple priors[C]. IEEE International Conference on Image Processing, Melbourne, Australia, 2013: 171-175. doi: 10.1109/ICIP.2013.6738036.
[17] ELL T A and SANGWINE S J. Decomposition of 2D hypercomplex Fourier transforms into pairs of complex Fourier transforms[C]. European Signal Processing Conference, Tampere, Finland, 2000: 1-4.
Color Image Adaptive Watermarking Algorithm Using Fractional Quaternion Fourier Transform
WANG Jinwei①②ZHOU Chunfei①WANG Shuiping①②CHEN Beijing①②SUN Xingming①②
①(&,&,210044,)②(,&,210044,)
Some existing color image adaptive watermarking algorithms do not fully utilize the color information in the adaptive process, or do not consider the holistic property of the components of a color host image. To overcome these drawbacks, this paper proposes a color image adaptive watermarking algorithm based on Fractional Quaternion Fourier Transform (FrQFT). Firstly, the texture, edge and color tone features of the blocks of the host image are extracted using the Human Vision System (HVS). After that, the embedding strength values of the blocks suitable to watermark embedding are set adaptively according to the extracted feature. Finally, the quantization index modulation and the multiple redundant embedding strategy are used to insert the watermark in the FrQFT domain with the adaptive strength. Experimental results show that the proposed algorithm is superior over the existing algorithm using Quaternion Fourier Transform (QFT) and the algorithm based on Fractional Fourier Transform (FrFT).
Color image; Adaptive watermarking; Quaternion; Fractional Fourier Transform (FrFT)
TP391
A
1009-5896(2016)11-2832-08
10.11999/JEIT160169
2016-02-25;改回日期:2016-07-01;
2016-09-08
陈北京 nbutimage@126.com
国家自然科学基金(61272421, 61572258, 61232016, 61572257),江苏省自然科学基金(BK20151530, BK20150925),江苏高校优势学科建设工程资助项目(PAPD),江苏省大气环境与装备技术协同创新中心资助项目(CICAEET)
The National Natural Science Foundation of China (61272421, 61572258, 61232016, 61572257), The Natural Science Foundation of Jiangsu Province (BK20151530, BK20150925), The Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), The Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology (CICAEET)
王金伟: 男,1978年生,教授,硕士生导师,研究方向为多媒体数字水印、加密与认证.
周春飞: 男,1992年生,硕士生,研究方向为数字图像水印.
王水平: 女,1977年生,副教授,研究方向为音频信号处理.
陈北京: 男,1981年生,副教授,硕士生导师,研究方向为彩色图像处理、彩色目标识别.
孙星明: 男,1963年生,教授,博士生导师,研究方向为网络与信息安全、物联网.
