神经网络敏感性分析的高光谱遥感影像降维与分类方法

高红民 李臣明 周 惠 张 振 陈玲慧 何振宇



神经网络敏感性分析的高光谱遥感影像降维与分类方法

高红民 李臣明*周 惠 张 振 陈玲慧 何振宇

(河海大学计算机与信息学院 南京 211100)

高光谱遥感影像由于其巨大的波段数直接导致信息的高冗余和数据处理的复杂，这不仅带来庞大的计算量，而且会损害分类精度。因此，在对高光谱影像进行处理、分析之前进行降维变得非常必要。神经网络敏感性分析可以用于对模型的简化降维，该文将该方法运用于高光谱遥感影像降维中，通过子空间划分弱化波段之间的相关性，利用差分进化算法(DE)优化神经网络结构，采用Ruck敏感性分析方法剔除掉对分类贡献较小的波段，从而实现降维。最后，采用AVIRIS影像进行实验，所提算法相比其他相近的降维与分类方法能获得更高的分类精度，达到85.83%，比其他相近方法中最优方法高出0.31%。

高光谱遥感影像降维；神经网络敏感性分析；子空间划分；差分进化；Ruck敏感性分析

1 引言

高光谱遥感影像不同于一般的多光谱遥感影像，它除了能够表达地球表面的2维空间信息之外，还增加了1维的光谱信息，因此整个高光谱遥感影像可以看作是一个“图像立方体”。随着波段数目的增加，高光谱遥感影像数据呈几何级数增长。高光谱遥感影像具有光谱分辨率高、波段数目多、数据量庞大、信息冗余度高等特点。这给存储、传输和处理高光谱遥感影像带来麻烦。因此，在对高光谱影像处理之前进行降维十分必要。降维分为特征提取和特征选择。波段选择减少一些不必要的波段，不仅可以降低分类过程的计算量，而且能够有效地避免“Hughes”现象。然而普遍采用的特征提取方法是将原始的特征空间经过线性或非线性的变换，投影到一个低维特征空间，是对各光谱波段间重新组合和优化，如主成分分析法，独立成分分析法等。其在投影之后原始波段的排列顺序发生了改变，波段与波段间的相关性也同样发生了变化。这就改变了原始的波段顺序，破坏了光谱的物理特性，导致光谱信息的丢失，影响了后续的分类精度。高光谱影像波段选择方法是从高光谱影像的全部波段中选择若干个波段出来代表所有波段，选择出来的波段组合要能在随后的分类处理中有效地提高分类精度。本文从波段对分类影响程度大小的角度出发来对高光谱影像实施降维。

神经网络敏感性分析是一种能定量地描述一个模型的输入端对输出端的影响程度。依据实际对这种影响程度进行排序，筛选出影响较大的输入属性而剔除掉对模型输出结果影响很小的输入属性从而简化模型，降低模型的复杂度。神经网络分类器是高光谱遥感影像分类方法中常用的分类器，它对于高维的、非线性结构的高光谱遥感影像具有良好的分类效果。因此，本文结合BP神经网络分类器[8,9]，采用神经网络敏感性分析方法定量地评价波段对于分类精度的影响大小，选择其中影响较大的波段组合从而实现降维。

2 神经网络敏感性分析

敏感性分析(sensitivity analysis)是神经网络研究领域中一个很重要的研究方面。其定义是假设模型表示为(为模型的第个属性值)，令每个属性在可能的取值范围内变动，研究和预测这些属性的变动对模型输出值的影响程度[10,11]。这种影响程度又可以被称为敏感性系数，敏感性系数可以定量地描述属性对输出值的影响。根据实际问题的需要，可以对敏感性系数进行排序，筛选出敏感性系数较大的属性而剔除掉对模型输出结果影响很小的属性，从而简化模型降低计算复杂度，也就是达到了降维的效果。

3 神经网络敏感性分析的高光谱波段选择

神经网络敏感性分析方法结合BP神经网络分类器可以在全波段空间内进行波段选择，挑选出那些对分类贡献大的波段组合从而实现高光谱影像的降维。为了能使得敏感性分析结果更准确，在执行敏感性分析之前，对高光谱遥感影像数据进行预处理，使用子空间划分方法来预选一些相关性弱的波段组合。为了避免BP神经网络初始权值阈值选择的盲目性，采用差分进化算法对BP神经网络进行优化。最后再利用优化后的BP神经网络执行敏感性分析，采用综合评判函数把所有测试样本点的敏感性分析结果综合起来，最终选择出对分类结果影响大的波段。具体实现如下。

3.1数据预处理

在进行神经网络敏感性分析之前，需要对原始的高光谱遥感影像进行预处理。原始的高光谱遥感影像波段数目众多，各波段之间存在着很强的相关性，因此选择相关性弱的波段作为输入端对于敏感性分析最终结果非常重要。解决上述问题的基本思路就是将全部波段划分为若干个子空间，然后再进行波段选择。文献[12]采用基于相关性过滤的自适应子空间分解(Adaptive Subspace Decomposition, ASD) 划分数据源的方法，该方法首先计算出两波段间的相关系数R,j，其中，和分别表示第和波段。R,j的取值范围为。相关系数的绝对值越大，表明波段间的相关性越强；越接近于0，相关性越弱。R,j的定义为

其中，对角线上是自相关系数，其值为1。设定相应的阈值，将的连续波段组合成新的子空间。通过调整的大小可以自适应地改变每个子空间的波段数量和子空间个数。随着的增加，每个空间内的波段数目减少，子空间个数将随之增加。由于高光谱影像波段间的相关性具有分块的特征。因此根据相关系数矩阵可以定量地反映出这种分块特征从而可以把相关性强的连续波段划分在一个子空间内。然后，再在各个子空间内选取波段构成波段组合从而降低波段之间的相关性。

3.2 差分进化算法优化BP神经网络

传统的BP神经网络存在一些缺陷和不足，如网络的学习收敛速度慢，隐含层的层数和隐含层神经元个数的选择没有理论依据，网络中的连接权值和阈值初始化选择具有盲目性等。为了给神经网络敏感性分析求取敏感性系数提供稳定的连接权值和阈值，需要对神经网络初始连接权值和阈值进行优化。通常采用遗传算法(GA)来优化BP神经网络，差分进化算法[16]与遗传算法非常相似，但差分进化算法涉及的参数更少，全局搜索能力强而且收敛速度快。因此，为了能使BP神经网络实际输出和期望输出之间的误差绝对值最小化，采用差分进化算法来优化BP神经网络。具体算法步骤如下：

步骤1 数据预处理。由数据预处理划分子空间，确定BP神经网络拓扑结构。

步骤2 种群初始化。由BP神经网络拓扑结构可以确定整个网络中的权值和阈值个数。假设网络中的权值和阈值总和为，差分进化初始种群个体的维数即为网络权值和阈值总和，对种群个体初始化。以BP神经网络训练误差的绝对值作为适应度函数并计算初始种群的适应度函数值。

步骤3 算法迭代。依次执行差分进化算法的变异操作、交叉操作。用变异个体包含的权值阈值进行BP神经网络训练，计算训练误差绝对值即适应度函数值。执行选择操作时变异个体的适应度值与原个体的适应度值做比较，选择较优个体作为种群的下一代。

步骤4 获取最优权值阈值。算法迭代结束后用最优个体包含的权值阈值初始化BP神经网络。其实现流程图如图1所示。

图1 差分进化算法优化BP神经网络流程图

3.3敏感性分析降维

基于输出变量对输入变量的偏导敏感性分析是一种针对前馈型神经网络(如BP神经网络)而提出的方法。该方法利用网络中的激活函数求偏导，计算输入数据对输出值的影响，具有计算简单、快捷的优势。本文采用文献[17]提出的一种基于偏导的敏感性分析方法(简称Ruck敏感性分析)来进行高光谱影像降维。

其中，w和v1分别表示输入层神经元到隐含层神经元的连接权值以及隐含层神经元到输出层神经元=1的连接权值。分别表示隐含层神经元的激活函数和输出层神经元=1的激活函数的偏导函数。由于输出神经元的激活为线性函数，即可以将式(3)改写为

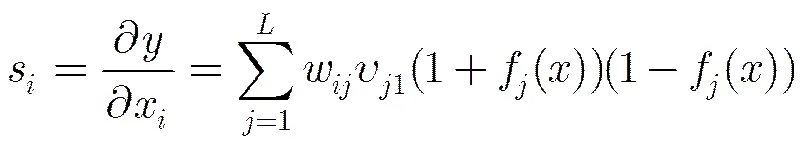
以上Ruck敏感性分析只是针对单个样本测试点输入值对输出值的敏感性分析，需要一个综合评判函数把各个单样本点的敏感性分析结果综合起来。此处选择由文献[18]提出的MSA度量指标作为综合评判函数。设S为所有测试样本输入变量对输出变量的敏感性系数。为第个测试样本输入变量对输出变量的敏感性系数。综合评判函数表示为

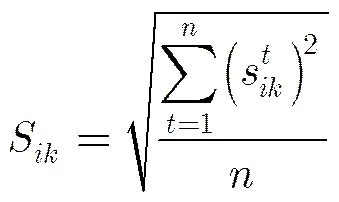
其中，表示样本的总数目，S为非负数。利用S可以对输入的波段对输出类别敏感性进行排序，从而确定输入变量对输出结果的影响程度的先后次序。

基于Ruck敏感性分析的高光谱影像降维的实现步骤如下，其流程图如图2所示。

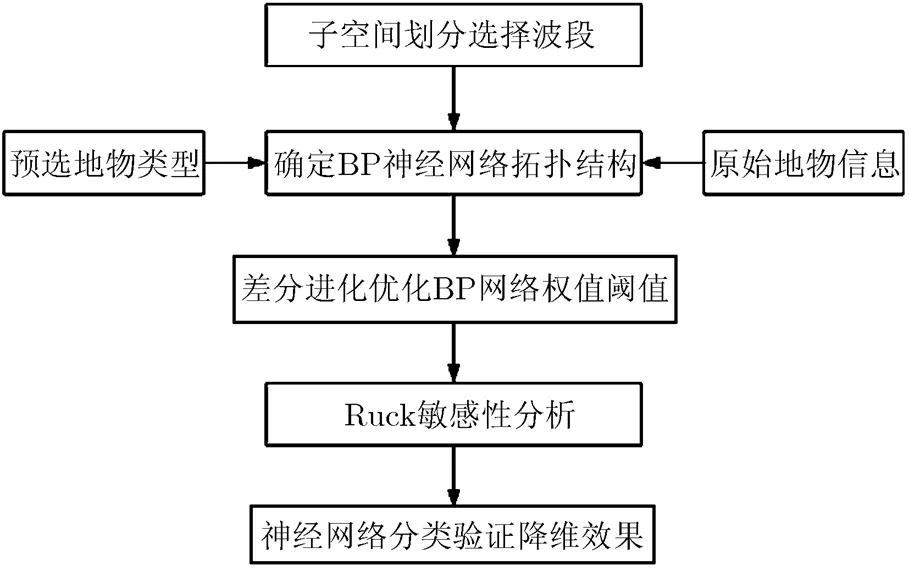
图2 基于Ruck敏感性分析的高光谱影像降维实现流程图

(1)对原始的高光谱遥感影像进行预处理，剔除干扰波段、预选地物类型，子空间划分等，确定BP神经网络的拓扑结构；

(2)差分进化算法对BP神经网络权值阈值进行优化；

(3)Ruck敏感性分析，根据敏感性系数进行排序，剔除掉敏感性系数较小的波段，筛选出对分类结果影响大的波段组合；

(4)使用BP神经网络分类器对筛选后的波段组合进行分类，验证降维的效果。

4 实验仿真与结果分析

本实验选取1992年6月在美国印第安纳州西北部遥感实验区拍摄的一部分AVIRIS高光谱遥感数据，波段数目为224。从原始波段中去除掉受水汽噪声等污染严重的波段(波段1~4, 78, 80~86, 103~110, 149~165, 217~224)，保留剩余的179个波段来进行试验。图3为试验选取第89, 5, 120波段合成假彩色图像。图4为原始地物分类定标图。选取影像中7类地物的样本参与分类实验。表1示出了7类地物的编号，名称，训练和测试样本数量。Ruck敏感性分析的前提条件是网络输出神经元只有1个，由于是对多类地物进行分类，因此输出变量采用的是实数形式而非二进制，这样一个输出神经元可以实现多个类别的分类。所有实验使用的波段组合均在相同的子空间划分下选择相同的波段进行。

图3 由89, 5, 120波段合成的假彩色图像   图4 原始地物分类定标图

表1训练样本和测试样本

类别编号类别名称训练样本测试样本 c1免耕玉米地 239 717 c2玉米幼苗 139 417 c3草地、树林 124 373 c4免耕大豆地 161 484 c5大豆幼苗 4111234 c6整理过的大豆地 102 307 c7木材 216 647 -总计13924179

采用基于相关性过滤的自适应子空间分解，求出各个波段间的相关系数值，由于数值过多，只列出其中部分波段的相关系数值如表2所示，AVIRIS相关系数矩阵灰度图如图5所示，AVIRIS相关系数曲线图如图6所示。灰度图中较亮的点表示相关系数较高的点，最亮的点代表相关系数为1，矩阵对角线的相关系数均为1，从相关系数矩阵灰度图来看，高光谱影像有明显的分块特性，因此利用波段间的相关性进行子空间分解可以合理地将波段分组，而在子空间内进行后续处理也可以有效地提高高光谱数据的处理速度。

图5 AVIRIS相关系数矩阵灰度图        图6 AVIRIS相关系数曲线图

为了使高光谱影像的分组特性较为明显，设定分解后的子空间数目为5，各子空间包含的波段集如表3所示，具体实验分组如表4所示。

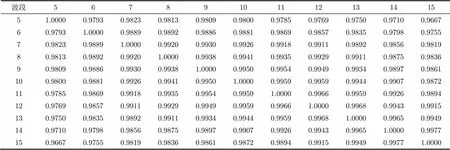
表2 5～15波段的相关系数值

表3 子空间分解维数及所含波段

表4 对比实验

每组实验各做3种不同波段数目情况的比较，前期本项目组研究发现，所选波段是总波段的时易达到分类精度的峰值，因此从划分好的子空间内按比例选取波段，波段总数大约为20, 30, 40构成实验所需的波段组合。BP神经网络的拓扑结构满足Ruck敏感性分析中的网络拓扑结构。设置输入端神经元个数等于每组实验的波段数目。输出层神经元个数= 1。隐含层设置为单隐层，其神经元个数设置为，其中为1~10之间的调节常数。BP神经网络训练和差分进化算法相关参数设置如表5和表6所示。

表5 BP神经网络训练参数设置

表6差分进化参数设置

参数名称参数值 个体维数DIDI=NL+L+LM+M 种群规模NdNd=20 迭代次数MaxDTMaxDT=50 杂交参数CRCR=0.9 差分进化变异模式DE/best/1/bin

图7为C和D两组实验在不同波段数目情况下，分别采用差分进化算法和遗传算法优化BP神经网络最优个体适应度值变化情况。

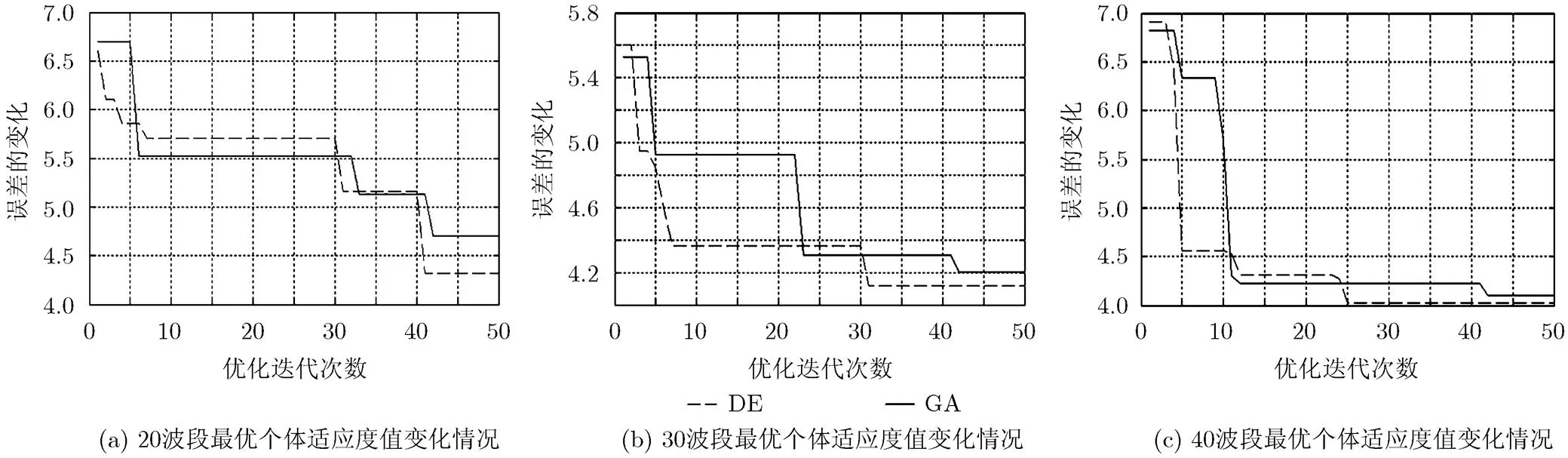
图7 最优个体适应度值变化

从图7的3幅折线图可以直观地看出，在各种不同波段数目情况下，多次迭代后基于差分进化算法优化的BP神经网络训练误差绝对值更小，说明采用差分进化算法优化BP的效果要优于使用遗传算法。

除了A组实验之外，其余3组实验都需要计算敏感性系数，考虑到敏感性系数值较多，表7~表9仅给出D组实验3种不同波段数目下经过Ruck敏感性分析后的敏感性系数值，按从大到小的顺序排列。

由表7~表9可以看到排在最后面的波段对应的敏感性系数已经很小，几乎不到排在最前面的敏感性系数的1/20。决定剔除掉敏感性系数值低于0.3的波段。再对降维后的不同波段组合进行BP神经网络分类，以验证经敏感性分析降维是否有助于提高分类精度。表10所示A, B, C, D 4组实验降维后波段组合参与分类实验得到分类精度。

从表10可以看出，在同一波段数目下C组和D组的分类精度比B组高，意味着对BP神经网络的权值阈值进行优化有助于提高敏感性系数的准确性，即敏感性系数更能真实地反映各个波段对分类结果的影响。其中，D组的分类精度又要高于C组，说明采用的差分进化算法优化BP神经网络最终得到的敏感性系数比C组使用遗传算法优化最终得到的敏感性系数更准确。A组不经过降维直接利用BP神经网络分类，其分类精度不如B, C, D组实验。说明采用40波段的神经网络敏感性分析降维较为有效。采用图8~图10给出实验20, 30, 40波段的分类结果图。

表7 20波段敏感性系数值

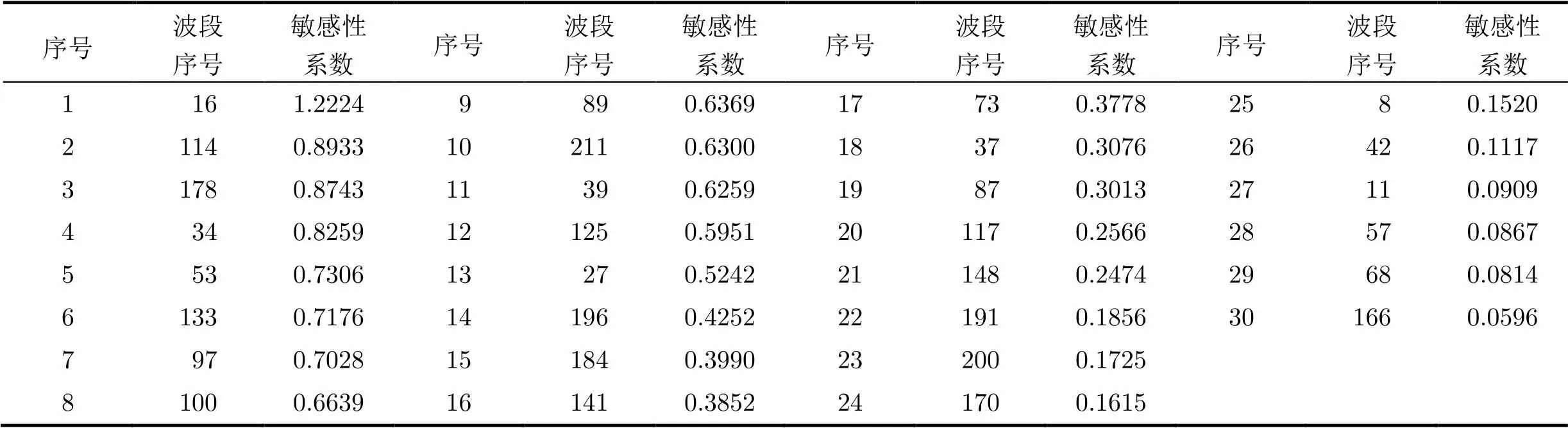
表8 30波段敏感性系数值

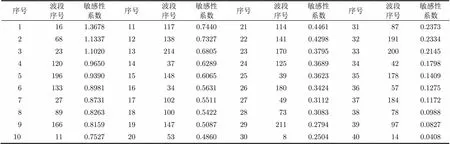
表9 40波段敏感性系数值

表10 4组实验最终分类精度结果(%)

在确定40波段的敏感性分析降维较为有效之后，将本文提出的敏感性分析波段选择和BP神经网络分类的方法(SA-BP)与现有的几种常用的降维与分类方法进行比较以对比其效果。这些方法包括：直接采用支持向量机(SVM)分类方法，遗传算法波段选择和SVM分类方法(GA-SVM)，及粒子群算法波段选择和SVM分类方法(PSO-SVM)，实验得到的最佳波段组合参与地物分类实验得到的生产者精度、用户精度和总体分类精度如表11所示，其中，PA表示生产者精度，UA表示用户精度。

从表11可以看出，SA-BP实验在生产者精度和用户精度总体上要优于其他3组实验，这就说明本文方法产生的漏分误差和多分误差相对较小。对比SVM和GA-SVM实验，虽然两者的总体分类精度仅相差0.1%，但是比较每一类地物的生产者精度和用户精度可以看出GA-SVM的分类方法要优于SVM的分类方法。对比GA-SVM和PSO-SVM，这两种算法在总体分类精度，生产者精度和用户精度上接近，并且均不如SA-BP分类方法有效。综上，神经网络敏感性分析降维与分类是有效的。

表11分类实验的生产者精度、用户精度和总体分类精度(%)

地物类别SVMGA-SVMPSO-SVMSA-BP PAUAPAUAPAUAPAUA c10.81230.83130.82390.82590.82650.82710.83420.8377 c20.81800.84730.80800.84040.83670.84650.83820.8516 c30.88620.86450.85770.86180.85470.86120.89790.8723 c40.81180.83810.81220.83840.82540.82950.81390.8424 c50.84880.82250.84230.82280.84300.83600.85420.8481 c60.82430.82440.83420.84200.82870.84420.85240.8608 c70.89320.89810.89240.89200.89380.89410.89580.8996 总体分类精度84.1884.2884.3385.83

图8 20波段分类结果图

图9 30波段分类结果图

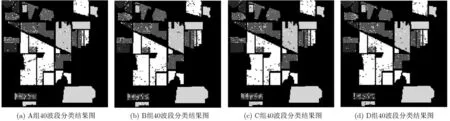
图10 40波段分类结果图

5 结论

结合敏感性分析的基本原理，本文提出将神经网络敏感性分析方法运用到高光谱遥感影像降维当中。考虑到尽可能地降低输入属性之间的相关性，采用自适应的子空间划分来选择波段组合，并利用差分进化算法优化BP神经网络，为神经网络敏感性分析提供稳定的网络连接权值和阈值，采用基于偏导的敏感性分析方法快速计算出敏感性系数，剔除掉系数很小的波段实现降维。通过设计多组对比实验，验证了提出方法的有效性。

[1] 杜培军, 谭琨, 夏俊士. 高光谱遥感影像分类与支持向量机应用研究[M]. 北京: 科学出版社, 2012: 6-35.

DU Peijun, TAN Kun, and XIA Junshi. Classification of Hyperspectral Remote Sensing Images and Applied Research of SVM[M]. Beijing: Science Press, 2012: 6-35.

TONG Qingxi, ZHANG Bing, and ZHENG Lanfen. Hyperspectral Remote Sensing-Principles, Techniques and Applications[M]. Beijing: Higher Education Press, 2006: 33-56.

[3] 吴倩, 张荣, 徐大卫. 基于稀疏表示的高光谱数据压缩算法[J]. 电子与信息学报, 2015, 37(1): 78-84. doi: 10.11999/ JEIT140214.

WU Qian, ZHANG Rong, and XU Dawei. Hyperspectral data compression based on sparse representation[J].&, 2015, 37(1): 78-84. doi: 10.11999/JEIT140214.

[4] GAO Hongmin, XU Lizhong, LI Chenming,. A new feature selection method for hyperspectral image classification based on simulated annealing genetic algorithm and choquet fuzzy integral[J]., 2013: 1-14. doi: 10.1155/2013/537268.

[5] GAO Lianru, LI Jun, KHODADADZADEH M,. Subspace-based support vector machines for hyperspectral image classification[J]., 2015, 12(2): 349-353. doi: 10.1109/LGRS.2014. 2341044.

[6] GURRAM P and KWON H. Coalition game theory based feature subset selection for hyperspectral image classification [C]. IEEE International Geoscience and Remote Sensing Symposium, Quebec, Canada, 2014: 3446-3449.

[7] FALCO N, BENEDIKTSSON J A, and BRUZZONE L. A study on the effectiveness of different independent component analysis algorithms for hyperspectral image classification[J]., 2014, 7(6): 2183-2199. doi: 10.1109/JSTARS.2014.2329792.

[8] 姜宇, 肖鸿, 刘兴鹏, 等. BP神经网络在异向介质基本结构分析中的应用[J]. 电子与信息学报, 2010, 32(1): 195-198. doi: 10.3724/SP.J.1146.2008.01703.

JIANG Yu, XIAO Hong, LIU Xingpeng,. Applications of BP neural network in analyzing metamaterials elemental basic structure[J].&, 2010, 32(1): 195-198. doi: 10.3724/SP.J.1146. 2008.01703.

[9] 张兵, 高连如. 高光谱图像分类与目标探测[M]. 北京: 科学出版社, 2011: 85-101.

ZHANG Bing, GAO Lianru. Hyperspectral Image Classification and Target Detection[M]. Beijing: Science Press, 2011: 85-101.

[10] 蔡毅, 邢岩, 胡丹. 敏感性分析综述[J]. 北京师范大学学报(自然科学版), 2008, 44(1): 9-16.

CAI Yi, XING Yan, and HU Dan. On sensitivity analysis[J].(), 2008, 44(1): 9-16.

[11] 张军, 刘祖强, 张正禄, 等. 基于神经网络和模糊评判的滑坡敏感性分析[J]. 测绘科学, 2012, 37(3): 59-62.

ZHANG Jun, LIU Zuqiang, ZHANG Zhenglu,. Susceptibility of landslide based on artificial neural networks and fuzzy evaluating model[J]., 2012, 37(3): 59-62.

[12] ZHANG Junping, ZHANG Ye, ZOU Bin,. Fusion classification of hyperspectral image based on adaptive subspace decomposition[C]. IEEE International Conference on Image Processing, Vancouver, BC, Canada, 2000, 3: 472-475.

[13] YU Feng and XU Xiaozhong. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network[J]., 2014, 134: 102-113. doi: 10.1016/j.apenergy.2014.07.104.

[14] LIU Ruixin, ZHANG Xiaodong, ZHANG Lu,. Bitterness intensity prediction of berberine hydrochloride using an electronic tongue and a GA-BP neural network[J]., 2014, 7(6): 1696-1702. doi: 10.3892/etm.2014.1614.

[15] 钱文江, 李同春, 丁林. 基于改进BP神经网络的库区渗漏量敏感性分析[J]. 三峡大学学报(自然科学版), 2012, 34(6): 23-27.

QIAN Wenjiang, LI Tongchun, and DING Lin. Sensitivity analysis of reservoir’s seepage discharge based on improved BP network[J].(), 2012, 34(6): 23-27.

[16] WANG Lin, ZENG Yi, and CHEN Tao. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting[J]., 2014, 42(2): 855-863. doi: 10.1016/j.eswa.2014. 08.018.

[17] RUCK D W, ROGERS S K, and KABRISKY M. Feature selection using a multilayer perceptrons[J]., 1990, 2(2): 40-48.

[18] ZURADA J M, MALINOWSKI A, and USUI S. Perturbation method for deleting redundant inputs of perceptron networks[J]., 1997, 14(2): 177-193. doi: 10.1007/978-3-662-45652-1_35.

Dimension Reduction and Classification of Hyperspectral Remote Sensing Images Based on Sensitivity Analysis of Artificial Neural Network

GAO Hongmin LI Chenming ZHOU Hui ZHANG Zhen CHEN Linghui HE Zhenyu

(,,211100,)

The high dimensions of hyperspectral remote sensing images will cause the redundancy of information and complexity of data processing, which also brings tremendous computing workload and damages application accuracy. Therefore, before the analysis of hyperspectral image processing, it is necessary to reduce the high dimensions of hyperspectral data. The Sensitivity Analysis (SA) of artificial neural network can be used in dimension reduction of the model. Now the Sensitivity Analysis of artificial neural network is applied to dimension reduction for hyperspectral remote sensing images in the paper. First of all, all bands are divided into several groups as long as a lower correlation exists between adjacent bands. Furthermore, Differential Evolution (DE) algorithm is used for optimizing neural network structure. Moreover, the bands which make small contribution will be given up based on Ruck sensitivity analysis method. Finally, experiments are conducted with AVIRIS images. The results show that the proposed method can get high classification accuracy of 85.83% at small training samples, 0.31% higher than the best one among other similar methods of dimension reduction and classification.

Dimension reduction for hyperspectral remote sensing images; Sensitivity Analysis (SA) of artificial neural network; Subspace decomposition; Differential Evolution (DE); Ruck Sensitivity Analysis (SA)

TP751.2

A

1009-5896(2016)11-2715-09

10.11999/JEIT160052

2016-01-13；改回日期：2016-06-08；

2016-09-01

李臣明 lichenming55@163.com

中央高校基本科研业务费项目(2014B13214, 2015B 26914)，十二五国家科技支撑计划项目(2015BAB07B03)，河海大学国家级大学生创新训练计划项目(201610294061)

The Fundamental Research Funds for the Central Universities (2014B13214, 2015B26914), The Projects in the National Science & Technology Pillar Program during the Twelfth Five-year Plan Period (2015BAB07B03), The National Undergraduate Training Program for Innovation and Entrepreneurship of Hohai University (201610294061)

高红民： 男，1983年生，博士，讲师，研究方向为图像处理与模式识别.

李臣明： 男，1969年生，副教授，硕士生导师，研究方向为图像处理、图像识别等.

周 惠： 女，1977年生，博士，讲师，研究方向为模式识别与人工智能.

张 振： 男，1985年生，博士，讲师，研究方向为图像处理与模式识别.