速度作用下非线性弹性地基上矩形薄板主共振
2016-10-13李兆瑞汪东林
李兆瑞,汪东林
(安徽建筑大学 土木工程学院,安徽合肥 230022)
速度作用下非线性弹性地基上矩形薄板主共振
李兆瑞,汪东林
(安徽建筑大学 土木工程学院,安徽合肥 230022)
本文基于非线性弹性地基模型及弹性理论,建立了非线性弹性地基上矩形薄板在移动车辆荷载作用下的非线性动力方程,运用Galerkin方法及多尺度法求得该系统主共振的幅频响应方程,以行车速度为调谐参数,分析阻尼系数、车辆荷载、板厚及相位差等参数对非线性弹性地基上矩形薄板在移动车辆荷载作用下主共振幅频响应的影响。结果表明:非线性弹性地基上矩形薄板在行车速度作用下主共振系统的非线性特点不明显,振幅-速度响应曲线接近对称,改变阻尼系数、车辆荷载等参数时对共振区间影响不大。在正常取值范围内,随着阻尼系数值增大振幅-速度响应曲线峰值减小;随着车辆荷载、板厚及相位差的增大振幅-速度响应曲线峰值增大。
主共振;幅频响应;矩形薄板;行车速度
0 引 言
近年来随着交通事业的快速发展,公路里程数大量增加。在进行公路路面、机场跑道等基础设施建设时总会遇到地基板的计算分析问题,所以研究非线性弹性地基上板的振动具有重要的现实意义。Sathyamoorthy[1-2]等对薄板非线性问题进行了研究。Gajiendar[3]、Nath[4]、Dumir[5]、邱平[6]等研究了非线性弹性地基上圆形薄板的振动问题。杨志安[7]等研究了非线性弹性地基上矩形薄板的非线性振动问题。肖永刚、杨翠屏[8]等研究了非线性Winkler地基上矩形薄板在移动荷载作用下的非线性动力问题。上述研究均未涉及到行车速度对非线性弹性地基板振动的影响。
本文主要研究行车速度作用下非线性弹性地基上矩形薄板的主共振,考虑行车速度对系统共振的影响。在研究系统的幅频响应时,大多数学者未考虑到行车速度对系统共振的影响或单纯的把其隐含到失调参数中来整体考虑参数变化时幅频响应曲线的改变,而未把行车速度作为一个单独变量来考虑,这样不能直接地反映问题[9]。文章通过变量代换把隐含在失调参数中的速度变量显含出来,直接研究振幅-速度响应曲线,这样比较直观地反映了行车速度对系统主共振的影响,在进行地基板设计时可以此作为参考因素。例如进行公路板设计时,其上的车辆行驶速度是必要的考虑因素。本文先是建立了动力学平衡方程,利用Galerkin方法把偏微分方程转化为了常微分方程,而后用多尺度法研究了系统主参数共振问题,最后讨论了不同参数改变时对系统主共振的影响。
1 单激励下系统主共振
1.1模型及基本方程的建立
如图1所示建立模型进行分析:假设对边简支矩形薄板,板厚为h,在板的左右边界上受有均匀分布的压力N,x和y方向上的长度分别为a和b,行车速度为v,受有横向车辆荷载 P1sinωt和并考虑有地基反力阻尼力,干扰力的存在

图1 模型图
根据力的平衡条件,可以建立动力学平衡方程如下所示:

其中E是弯曲刚度,υ是泊松比,k1和k2分别为线性和非线性地基系数,δ是阻尼系数,ρ是板的密度,N是纵向荷载,W是板的横向挠度,h是板厚,P1sinωt和P2sin(ωt-θ)是横向车辆荷载。其余的表达式表示如下:
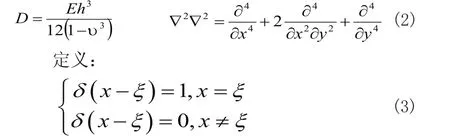
边界条件为:

假设满足边界条件的位移方程为:
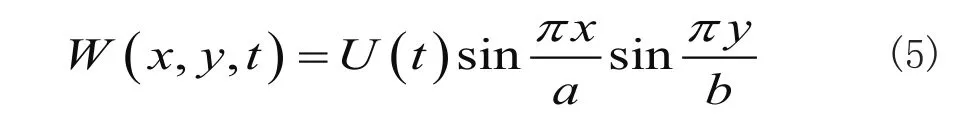
将方程(5)代入到方程(1)中将会产生残差。为了限制残差,可以通过伽辽金方法来建立求解过程。其中纵向荷载方程采用分部积分、和差化积后可得到[10]:

由于式(6)比较繁琐至研究起来不便,可以简化其形式如下:

式(7)中的字母具体表示如下:

1.2主共振的幅频响应
主共振是指激励频率接近于派生系统固有频率时的共振[11]。如果系统是线性小阻尼系统,这时很小的激励幅值F都可以激发出强烈的共振。因此研究系统的主共振时应该对系统阻尼、外激励幅值和频率加以限制,以下为限制条件:

其中0 ≤ε<1,σ被称为激励频率失调参数。下面分析激励为F1cosω1t时的情况,考虑P0=0简化纵向力,此时ω02的表达式如下:

在以上的限制条件下,式(7)可变形为:

研究上述方程的一次近似解时只需要两个时间尺度,可设:

上述偏微分方程中第一式的解为:
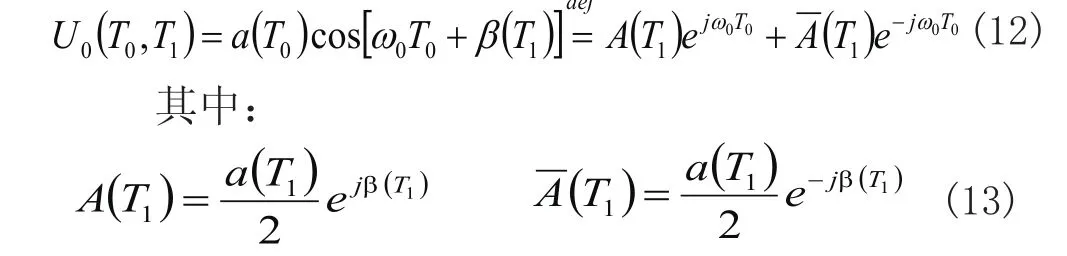
将式(12)、(13)代入(11)式中第二式的右端,可得到消除永年项的条件为:

将式(12)代入到(14)中并应用欧拉公式分离实部和虚部可得到:

这就是一次近似解(10)的慢时变振幅和相位应满足的微分方程。引入(16)后,方程(15)还可转化为自治微分方程(17):

令式(17)中D1a =0、D1ϕ=0可得到振幅和相位应满足的代数方程,而后平方化简得可到幅频响应方程。方程采用原系统参数来表示,其中字母通过上文的限制条件进行代换:
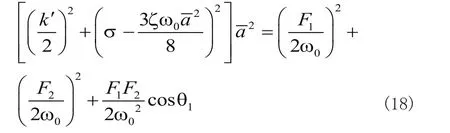
2 行车速度作用下系统主共振
2.1行车速度对系统主共振幅频响应影响
本文是研究行车速度作用下系统主共振,则其振动必然受到行车速度的影响[12]。在式(18)中出现了ω0,比较ω1=ω0+εσ与上文中出现的可知,速度v与激励频率失调参数σ之间存在变量代换。在正常取值范围内可规定ω=ω0,由0≤ε<1可假设ε的取值为0.1。通过变量代换把速度v显含到设计格式中,可直接体现出速度变化时其系统主共振相应振幅的改变,这样可直接观察到行车速度对系统振幅的影响,在进行公路路面及地基板设计时也可作为参考因素。例如在进行路面设计时,板的振动及其振幅的大小必然受到其上车辆行驶速度的影响。
根据上述的变量代换把速度显含到设计格式中,式(18)变动如式(19):
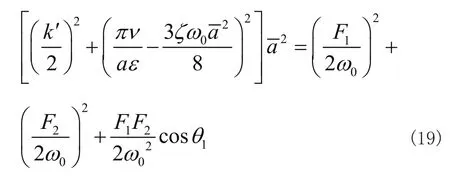
2.2计算实例
移动车辆荷载作用下的矩形薄板系统取值如下:
阻尼系数:δ=0.1,密度:ρ=2.5×10³ kg/m³,
矩形板厚:h=0.2 m,泊松比:υ=0.15,车轴间距:d=2 m, 相位差:θ=π/3,ε=0.1,
弹性模量:E=3.5×109pa,矩形板长:a=3.5 m, 矩形板宽:b=4 m,
其中k1和k2分别为线性和非线性地基系数,其取值根据土的性质查地基系数表可知。
利用了MATLAB软件[13-14],按式(19)计算矩形薄板在移动车辆荷载作用下的主共振的影响曲线:
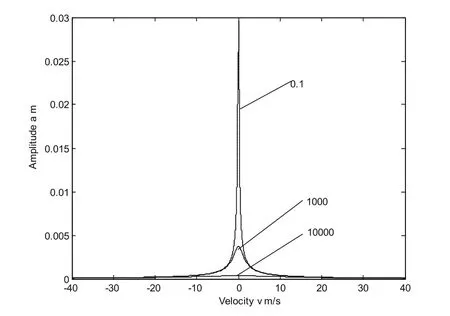
图2 振幅-速度响应曲线(不同阻尼系数)

图3 振幅-速度响应曲线(不同车辆荷载)

图4 :振幅-速度响应曲线(不同板厚)

图5:振幅-速度响应曲线(不同相位差)
图2至图5描述的是不同参数影响下的振幅-速度响应曲线,即表示随着速度的改变其振幅也会出现相应变化。图中的速度正负表示其车辆行驶方向的正负,规定沿x轴正方向为正,则反之为负。
从图2可以看改变阻尼系数对振幅-速度响应曲线的影响,系统非线性特点不明显,曲线接近对称。若是强非线性系统,曲线会很明显偏向一边。随着阻尼系数的增加,其曲线的峰值将会减小;反之增大。由式(19)可以看出:阻尼系数数量级为十分位数,密度为千分位数,厚度为十分位数,其平方值为无限小,所以在正常取值范围内其阻尼系数的改变对整个曲线没有明显影响。
图3反映了改变车辆荷载对振幅-速度响应曲线的影响,即随着车辆荷载的增加曲线的峰值将会增大;反之减小。改变车辆荷载时系统的共振区间变化不大。在实际应用中随着路面通过车辆载重的增加,路面板的振动幅度将会增大,与图表示内容相符。
不同板厚对振幅-速度响应曲线也具有影响,从图4可知随着板厚的改变,其系统共振区间变化不大。板厚增加时曲线的峰值变大;反之减小。由式(19)可以推导出板厚改变可影响其振幅的大小。
改变相位差也会影响振幅-速度响应曲线,由图5可知该系统非线性特点不明显,改变相位差时其共振区间变化不大。随着相位差的增加曲线振幅将会增大;反之减小。
3 结论
本文运用Galerkin理论及多尺度法,建立了非线性弹性地基上矩形薄板在车辆移动荷载作用下的主共振幅频响应方程,把速度作为调谐参数来研究其对系统主共振的影响。通过把速度显含到设计格式中可以比较直观的反映行车速度系统主共振的影响,在进行地基板设计时也可以此作为参考因素。利用MATLAB软件分析了改变阻尼系数、车辆荷载、板厚、相位差等对系统主共振振幅-速度响应曲线的影响,所得的结论对工程实际具有参考价值。研究结果表明:非线性弹性地基上矩形薄板在行车速度作用下主共振系统的非线性特点不明显,振幅-速度响应曲线接近对称,改变阻尼系数、车辆荷载、板厚、相位差等参数时对系统共振区间影响不大。在正常取值范围内,随着阻尼系数值增大振幅-速度响应曲线峰值减小;随着车辆荷载、板厚及相位差的增大振幅-速度响应曲线峰值增大。
[1]袁尚平,张惠桥,王冰.参数激励下简支板的分岔与混沌[J].太原重型机械学院学报,1997,18(2):133-139.
[2]韩强,杨桂通.非线性大挠度矩形板中内共振导致的分叉[J].固体力学学报,2001,22(2):199-204.
[3]Ajiendar N. Large amplitude vibrations of plates on elastic foundation[J]. International Journal of Nonlinear Mechanics, 1967, 2(1):163-168.
[4]Nath. Large amplitude response of circular plate on elastic foundation[J]. International Journal of Nonlinear Mechanics, 1982, 17(4):285-296.
[5]Dumir P C. Nonlinear vibration and postbucking of isotropic thin circular plate on elastic foundation[J]. Journal of Sound and Vibration, 1986, 107(2):253-263.
[6]邱平,王新志.非线性弹性地基上的圆薄板的分岔与混沌问题[J].应用数学和力学,2003,24(8):779-784.
[7]杨志安,赵雪娟,席晓燕.非线性弹性地基上矩形薄板的非线性振动与奇异性分析[J].振动与冲击,2006,25(05):69-71.
[8]肖勇刚,杨翠屏.非线性Winkler地基上矩形薄板在移动荷载作用下的非线性动力分析[J].应用力学学报,2015,32(01):108-111.
[9]李小珍,朱艳,强士中.高速列车作用下简支梁车桥耦合振动随机响应分析[J].振动与冲击,2006,25(05):69-71.
[10]杨志安,赵雪娟,席晓燕.非线性弹性地基上矩形薄板的主参数共振[J].岩土力学,2005,26(12):1921-1925.
[11]杨志安,赵雪娟.温度场中非线性弹性地基上矩形薄板的主共振-主参数共振[J].应用力学学报,2009,26(01):126-129.
[12]王昆鹏,夏禾,郭薇薇,等.移动荷载列作用下简支梁振动响应参数研究[J].振动工程学报,2014,27(03):362-365.
[13]尚涛,谢龙汉,杜如虚.MATLAB工程计算及分析[M].北京:清华大学出版社.2007.
[14]石博强,赵金.MATLAB数学计算与工程分析范例教程[M]. 北京:中国铁道出版社,2005.
The Main Resonance of Rectangular Thin Plate on Nonlinear Elastic Foundation with the Effect of Velocity
LI Zhaorui,WANG Donglin
(School of Civil Engineering,Anhui Jianzhu University,Hefei,230022,China)
Based on the model of the nonlinear elastic foundation and the elastic theory, this paper establishes the nonlinear dynamic equation of rectangular thin plate on the nonlinear elastic foundation under the load of moving vehicles. Using the Galerkin method and the method of multiple scales, the amplitude frequency response equation of the main resonance in this system can be obtained. Taking the driving speed as the turning parameter, this paper analyzes the impact of the damping coeffcient, vehicle load, the plate thickness and phase difference. The result indicates that on the nonlinear elastic foundation, with the effect of driving speed, the nonlinear characteristics of the main resonance system of the rectangular thin plate are not obvious; the amplitude-velocity response curve is close to the symmetry; and the impact of the changes of damping coeffcient and vehicle load on the resonance range is small. In addition, in the normal range, with the increase of the damping coefficient, the peak of the amplitude -velocity response curve decreases; and with the increase of the vehicle load, the plate thickness and the phase difference, the peak of the amplitude-velocity response curve also increases.
main resonance; amplitude frequency response; rectangular thin plate; driving speed
TU348
A
2095-8382(2016)04-045-05
10.11921/j.issn.2095-8382.20160410
2016-03-01
2014年安徽省级质量工程项目(2014tszy023), 2015年省教育厅教学研究重点项目(2015jyxm252).
李兆瑞(1993-),女,硕士研究生,主要研究方向为地下结构计算理论与应用。
