大跨度斜拉桥双边箱梁剪力滞效应研究
2016-10-13谢朋林
谢朋林,胡 成
(合肥工业大学 土木与水利工程学院,安徽合肥 230009)
大跨度斜拉桥双边箱梁剪力滞效应研究
谢朋林,胡 成
(合肥工业大学 土木与水利工程学院,安徽合肥 230009)
为明确宽幅薄壁双边箱梁斜拉桥在最大悬臂施工阶段主要荷载对剪力滞效应的影响,以某斜拉桥为研究对象,采用有限元方法计算分析了混凝土双边箱梁截面在不同荷载单独作用及组合作用下的剪力滞效应。分析表明,自重作用下,距离塔根越近,箱梁剪力滞效应越明显;斜拉索索力对主梁剪力滞效应影响规律与自重类似;纵向预应力作用下,全桥剪力滞效应不明显;通过调整纵向预应力及斜拉索索力参数,可以优化双边箱梁的剪力滞效应。
斜拉桥;双边箱梁;最大悬臂;剪力滞;正应力
0 引 言
在梁桥中,剪力滞系数定义为考虑剪力滞效应后的弯曲应力与按初等梁理论计算的弯曲应力之比。国内外许多学者对剪力滞效应研究提出了许多理论和计算方法,取得了丰硕成果[1-5],不过研究对象以简支梁和连续梁桥的单箱单室箱梁居多[6-8],对于具有多个连续弹性支撑,且同时承受弯矩和轴力的超静定双边箱梁斜拉桥研究较少。
双边箱梁斜拉桥是一种自重轻、便于悬臂施工、承载能力强的斜拉桥形式,规范对双边箱梁剪力滞系数的规定较少。既有研究表明,箱梁截面剪力滞效应在施工过程中对结构的影响较成桥后更大,结构的最不利受力状态可能处于施工过程中[9]。
目前剪力滞理论的研究方法主要有解析理论法和数值解法,而解析理论法已经不能符合高次超静定结构分析的要求,随着计算机技术的迅速发展,数值解法中的有限元法在箱梁截面剪力滞分析中占据越来越重要的地位。本文采用空间有限元法,对最大悬臂施工阶段的某双边箱梁斜拉桥进行剪力滞效应研究。
1 研究背景
某斜拉桥为双塔三跨双索面半漂浮体系斜拉桥,全长620 m,跨径布置为(150+320+150) m(图1)。主梁材料为C55混凝土,采用双边薄壁箱梁断面形式,梁宽31 m,高3.2 m。主塔材料为C50混凝土,采用箱型断面形式。斜拉索材料为1860钢绞线,采用扇形布置。该桥主梁上索距布置为:边跨索距为5×4.5 m+11×7 m+5×6.8 m;中跨索距为5×6.8 m+16×7 m。横隔板板厚40 cm,每段主梁设置一道。
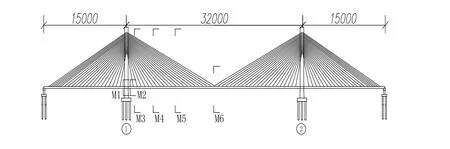
图1 斜拉桥总体布置图 (单位:cm)
2 有限元模型建立
2.1计算参数
根据设计,选取主梁材料为C55混凝土,容重为ρ=26 kN/m³,弹性模量 E=3.5×104 MPa,泊松比γ=0.17;预应力钢束为Φ15.2钢绞线,标准强度fpk=1860 MPa,弹性模量Ep=1.95×105 MPa。斜拉索的索力取自有限元分析程序Midas civil的计算结果,并以集中力的形式作用在模型中。
2.2有限元模型
通过有限元程序 MIDAS/FEA 对该斜拉桥桥进行有限元分析,由于结构对称取一半结构建立模型,以1#号墩桥面中心点坐标为(0,0,0),向中跨方向建立0#~23#号块梁段模型。操作步骤如下:①建立局部桥梁三维模型,主梁模拟为实体单元、预应力钢束模拟为线单元、斜拉索索力采用集中力的形式添加到指定节点,斜拉索从塔根向跨中索号依次为:C1,C2,…C22, 拉索最大悬臂状态恒载索力见表 1。分析共划分84345个实体单元,10429个节点,模型见图2;②计算不同恒载作用下塔根、中跨处断面的剪力滞效应影响,截面标号分别为M1(X=1.5 m),M2(X=3.5 m),M3(X=6.1 m),M4(X=40.1 m),M5(X=81.9 m),M6(X=150 m),塔梁中轴连线交点为原点X=0。③计算在自重、预应力和斜拉索索力单独作用下中跨不同断面的剪力滞效应,并考虑不同荷载系数组合对断面剪力滞效应的影响。
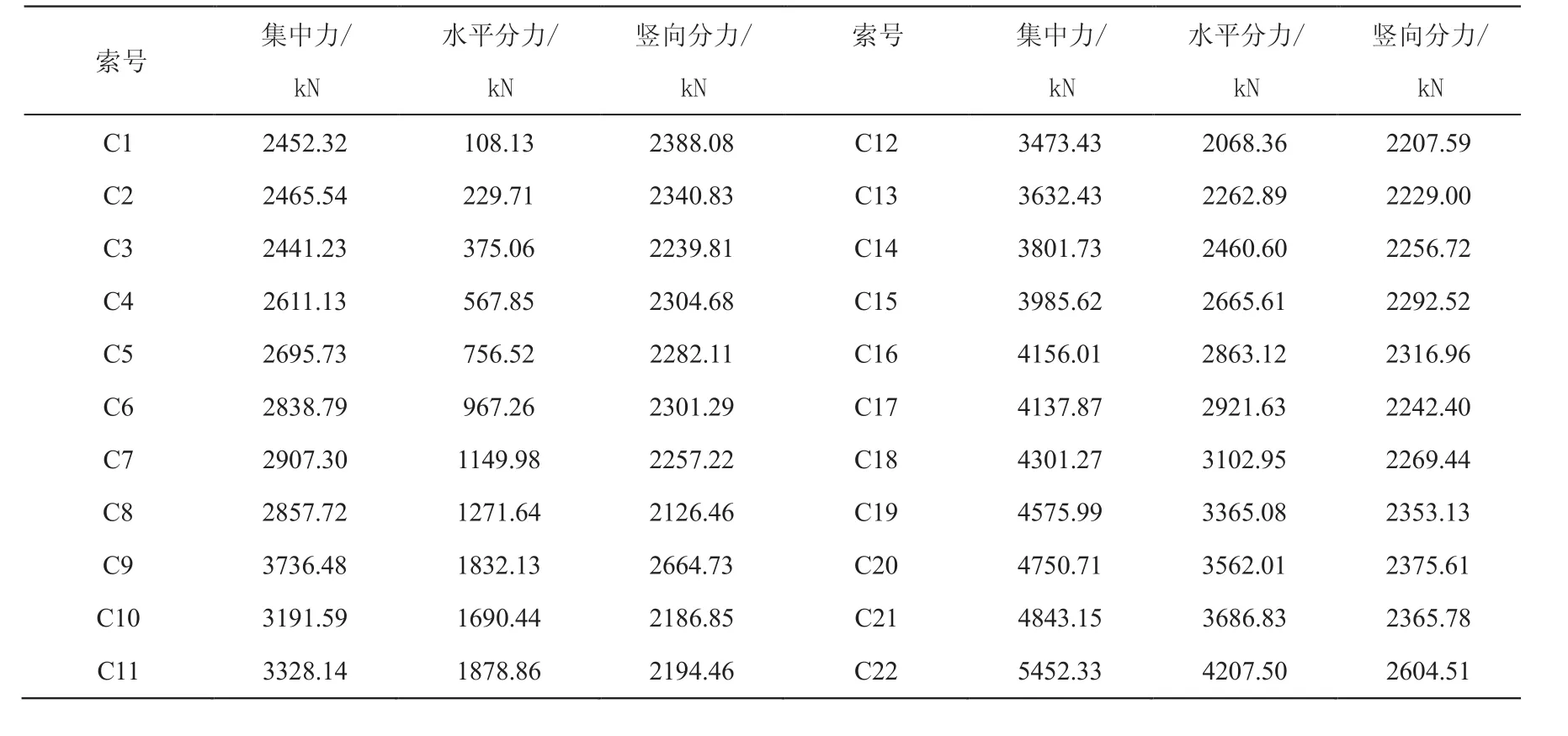
表1 最大悬臂状态索力表

图2 局部有限元模型
3 结果分析
在图3-图6应力计算数值中拉应力为正,压应力为负。由于该桥箱梁顶板的剪力滞现象较底板更为突出,故结果分析中不给出底板剪力滞特性,仅给出顶板剪力滞的变化特性。

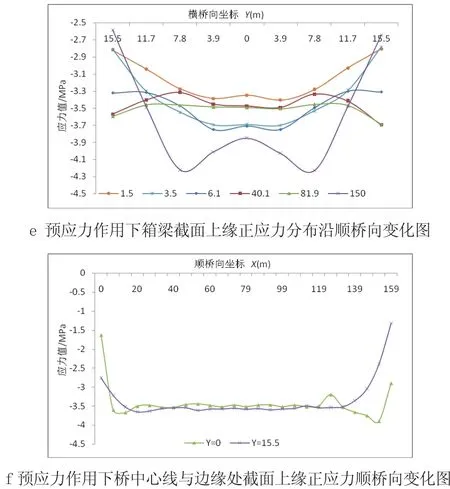
图3 主要荷载作用下不同位置箱梁截面上缘正应力图
3.1自重
图 3a,3c,3e为X=1.5,3.5,6.1,40.1,81.9,150 m处箱梁截面上缘应力变化曲线,每根曲线表示不同的位置,值越大表明距塔根越远悬臂越大;横坐标即横桥向坐标,纵坐标为应力值。图3 b,3d,3f为桥中心线处(Y=0 m)与边缘处(Y =15.5 m)箱梁截面顶缘沿顺桥向应力变化曲线,横坐标即顺桥向坐标,纵坐标为应力值。
由图3a可知,在自重单独作用下,距离塔根越近,箱梁剪力滞效应越明显,箱梁截面的剪力滞系数越大。塔根处(X=0 m)顶板应力骤减,这是因为塔根处箱梁为实腹式截面,大大增加了截面面积故应力值骤减。从图3b中可以看出,距离原点距离越远,梁中线处应力与边缘处应力越接近,梁中心与梁边应力比值越小,即剪力滞效应越不明显。
3.2索力
在斜拉索索力作用下, 箱梁截面上缘应力分布规律与重力作用时基本相同,符号相反。图3d为梁中心线与梁边缘应力比值图,剪力滞系数规律与重力单独作用时基本一致。距离塔根越近,箱梁剪力滞效应越明显,箱梁截面的剪力滞系数越大。当X趋近最大悬臂端(X=158.9 m)时,梁中心线与梁边缘应力比值趋于1.0。
斜拉索水平分力对箱梁截面剪力滞效应的影响远小于竖向分力。由表2和图4可知,斜拉桥箱梁截面正应力的不均匀分布是由轴向应力、弯曲应力的不均匀分布共同导致,在斜拉索水平分力作用下,塔根处箱梁横截面最大应力差为22 MPa;在斜拉索竖向分力作用下,塔根处箱梁横截面最大应力差为667 MPa,竖向分力对箱梁截面正应力的不均匀分布影响更大,即竖向分力对箱梁截面剪力滞效应的影响远大于水平分力。

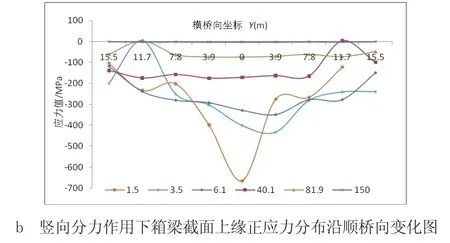
图4 索力分量作用下不同位置箱梁截面上缘正应力图
3.3预应力
在纵向预应力荷载作用下,截面应力分布较均匀,剪力滞效应不明显, 全桥纵向X =13.2~139 m范围内梁中心线与边缘应力比值在1.0附近。这是因为相比自重和斜拉索索力作用,纵向预应力荷载以相等的轴力较均匀的施加在箱梁顶板上,顶板横桥向各点受到相同的轴力作用,相互影响几乎为零,故剪力滞效应不明显。

表2 索力分量作用下截面上缘正应力表 单位:(MPa)
3.4荷载组合
考虑自重、预应力和斜拉索索力共同作用,分析箱梁截面顶板应力分布及剪力滞系数规律。为了使箱梁顶板截面剪力滞效应降到最小,应力分布更加均匀,对不同荷载系数进行调整,文中采用如下5种工况,并以同一断面边缘点(Y=15.5 m)与中心线点(Y=0 m)应力比值来反映调整效果,结果如图6所示。
工况1:1.0自重+1.0预应力+1.0斜拉索索力;
工况2:1.0自重+1.1预应力+1.0斜拉索索力;
工况3:1.0自重+1.0预应力+0.9斜拉索索力;
工况4:1.0自重+1.1预应力+0.9斜拉索索力;
工况5:1.0自重+0.8预应力+1.0斜拉索索力。
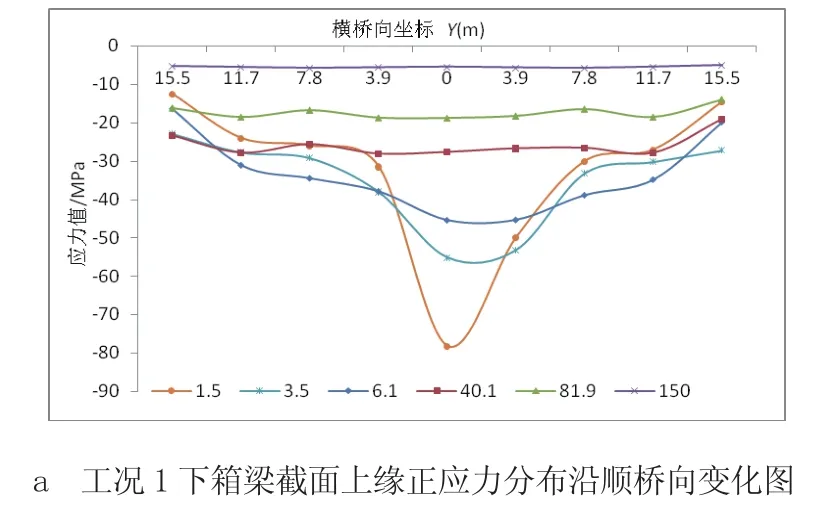

图5 工况1下不同位置箱梁截面上缘正应力图
自重、预应力和斜拉索索力共同作用下,箱梁应力值变小,这是因为斜拉索竖向分力与重力对主梁作用相互抵消。应力分布规律与斜拉索索力单独作用基本相同,纵向预应力对应力分布影响有限。图5b为工况1作用下梁中心线与梁边缘应力比值图,剪力滞系数规律与索力单独作用时基本一致。
由图6可知,纵向预应力增加10%,减小20%,梁中心与梁边沿应力比值变化不大;斜拉索索力减小10%梁中心与梁边应力比值明显增大,比值更接近1.0。相比纵向预应力,斜拉索索力对截面剪力滞效应影响较大,箱梁截面剪力滞系数对索力参数更敏感。工况4作用下,即当增加10%预应力同时减小10%斜拉索索力时,箱梁截面剪力滞效应得到一定的优化。通过适当调整纵向预应力及斜拉索索力的参数,可以优化双边箱梁的剪力滞效应。

图6 不同工况下桥中心线与梁边缘处截面上缘正应力比值
4 结论
1.在自重单独作用下,距离塔根越近,箱梁剪力滞效应越明显,箱梁截面的剪力滞系数越大。
2.斜拉索索力单独作用下,主梁应力分布规律、剪力滞系数规律与自重作用基本相同。斜拉桥箱梁截面的正应力由轴向应力和弯曲应力两部分组成,斜拉索竖向分力对箱梁截面正应力的不均匀分布影响更大,竖向分力对箱梁截面剪力滞效应的影响远大于水平分力。
3.纵向预应力荷载作用下,全桥纵向X=13.2 ~139 m范围内梁中心与翼缘的应力比值在1.0附近,剪力滞效应不明显。
4.通过调整自重、纵向预应力及斜拉索索力的系数,可以优化双边箱梁的剪力滞效应。相比纵向预应力,斜拉索索力对截面剪力滞效应影响较大,箱梁截面剪力滞系数对索力参数更敏感。
[1]陈水生,田正龙,桂水荣.单箱多室波形钢腹板箱梁剪力滞研究[J].公路交通科技,2015,32(7):69-75.
[2]蔺鹏臻,刘应龙,孙理想,等.预应力作用下简支箱梁桥的剪力滞效应分析[J].铁道工程学报,2014,(11):54-58.
[3]郭伶.连续箱梁桥施工阶段负剪力滞效应研究[J].公路与汽运,2015(1):138-143.
[4]雒敏,蔺鹏臻,孙理想.单箱双室箱梁的剪力滞效应分析[J].力学与实践,2013,35(6):70-74.
[5]方飞,张杰,张鲲,等.小半径单箱双室曲线桥梁翼缘有效宽度的研究[J].合肥工业大学学报(自然科学版),2013,36(9):1088-1092.
[6]罗旗帜.基于能量原理的薄壁箱梁剪力滞理论与试验研究[D].长沙:湖南大学,2005.
[7]李小祥,石雪飞,阮欣,等.低高度混凝土单箱单室宽箱梁剪力滞效应研究[J].结构工程师,2008,24(2):43-47.
[8]黄刚.超宽单箱单室箱梁剪力滞效应分析[J].公路交通技术,2010(4):56-58.
[9]周伟,蒋益飞.斜拉桥最大双悬臂施工阶段主梁剪力滞效应分析[J].公路,2008(6):59-64.
Shear lag effect analysis of bilateral box girder of long-span cable-stayed bridge
XIE Penglin, HU Cheng
(HeFei University of Technology,School of civil engineering,Hefei,230009,China)
In order to determine the effect of main loadings on the construction stage of the maximum cantilever on shear lag effect in bilateral box girder of concrete cable-stayed bridge with wide and thin wall, the shear lag effect of concrete bilateral box girder of a cable-stayed bridge under different loads of both independent action and composite actions with the fnite element method was calculated and analyzed. The analysis showed that the shear lag effect of box girder was more obvious when it was closer to the tower under dead weight; In addition, the effect of the law of cable force on the shear lag effect of the main girder is similar to the weight of the girder; The shear lag effect of the whole bridge is not obvious under longitudinal prestress; The shear lag effect of bilateral box girder can be optimized by adjusting the longitudinal prestress and the cable force parameters.
cable-stayed bridge;bilateral box girder;maximum cantilever;shear lag;normal stress
U445
A
2095-8382(2016)04-026-05
10.11921/j.issn.2095-8382.20160406
2016-01-19
谢朋林(1989-),男,硕士研究生,研究方向为大跨度桥梁的施工控制与仿真分析。
