钢曲杆在高温（火灾）下的力学特征数值分析

赵雄夫，孙 强，郭 薇

（安徽建筑大学土木工程学院，安徽合肥 230601）

钢曲杆在高温（火灾）下的力学特征数值分析

赵雄夫，孙 强，郭 薇

（安徽建筑大学土木工程学院，安徽合肥 230601）

高温（火灾）环境下钢曲杆的受力和变形将会产生较大变化，对结构的力学特征影响较大。本文根据结构稳定理论和热力学原理，应用有限元分析方法，结合三种不同工况，分别探讨了高温（火灾）环境下不同支座形式、杆截面形式等因素对钢曲杆力学特征的影响，并对三种工况下钢曲杆力学特征进行了数值分析与对比，得出了H型钢截面无铰钢曲杆更加符合建筑安全要求的结论，研究成果可为钢曲杆抗火研究提供参考。

钢曲杆；高温（火灾）；力学特征；有限元；数值分析

0　引　言

随着钢结构建筑的快速发展，钢曲杆作为一种重要的钢构件在建筑工程中得到了广泛应用。钢曲杆在竖向荷载作用下产生水平推力，将外荷载产生的弯矩转化为轴向压力，所以具有较高的承载能力。但是由于钢结构本身不耐火的特性，在高温（火灾）环境下，钢结构的力学性能会发生很大改变［1］，因此对钢曲杆在高温（火灾）下的力学性能研究非常重要。二十世纪三十年代,英国人就已经对单独的钢构件进行火灾下的试验［2］；九十年代，英国某公司对一栋高八层钢框架进行了多次受火试验，这就是非常有名的卡丁顿试验，通过这个试验得到了大量的试验数据与结论［3］-［5］；国内李国强等人做了许多相关试验，重点研究钢结构在高温下承载力变化，推导出了钢结构力学特性伴随温度变化的规律及有关的计算公式，并在大量理论与试验研究的基础上制订了我国首部抗火规范《建筑钢结构防火技术规程》［6］-［8］，屈立军对火灾下钢结构进行了相关试验，试验表明，保持温度一定，对钢材进行加载时钢材的强度大于载荷一定时对钢材施加温度荷载情况下钢材的强度［9］；国内其他学者也对钢结构抗火做过大量研究［10］-［16］。

本文从单个构件出发，以单个钢曲杆为研究对象，利用有限元软件，对工程中常见的三种形式的钢曲杆进行抗火分析，为今后钢曲杆抗火研究提供理论依据。

1　钢曲杆热分析

通过稳态热分析，确定钢曲杆构件表面环境温度后再进行整体的结构热应力分析。结构分析之处应将单元从热单元转换为结构单元，其次定义材料的力学性能参数，最后需要设定的是进行结构分析时所需施加的各种外荷载包括热分析得到的热荷载与边界限定条件一起，施加到模型上进行应力分析。随后分析求解，即可得到在高温（火灾）作用下钢曲杆位移随时间变化图，最后对钢曲杆位移及应力应变分布图的数据进行列表并分析处理。

2　高温下钢构件的物理参数

（1）比热容：钢结构材料的比热虽然随温度变化但其值仍相对较小，当温度升高超过725 ℃时，其比热则迅速增加。由于材料的比热变化过大，通常情况下，计算实用温度时，通常忽略其与温度的关系取在其范围内的平均值cs=600。

（2）热传导系数：在温度达到750 ℃之前系数值都随温度成线性增长，超过之后则基本不随温度改变。当进行实际工程计算，钢材的厚度不属于较厚时，可以采用假定的与温度无关的热传导系数值，EC3和 EC4建议取λs=45。

（3）热膨胀系数：在0～700 ℃范围内，系数随温度升高近似成线性增加。目前，根据《钢结构设计规范》，一般采用不受温度影响改变的值αs=1.2×105。

（4）密度：大跨钢拱结构单位密度通常取为：ρs=7850 kg³。

3　工程实例

工况一：钢曲杆采用等截面圆钢管，钢曲杆跨长6 m，矢跨比1/6，E1=E2=2.06×108 KN/m²，圆钢管外径D=203 mm，圆钢管内径d=191 mm，圆钢管截面面积A1=37.13 cm²，结构整体惯性矩I1=1803.07 cm4，以下各图中，M为拱截面内力，Ts为温度，f为钢材极限强度标准值。着火位置设定在钢曲杆的外表面某一面。此工况采用两铰钢曲杆模型。

工况二：材料参数与模型一相同，此模型采用无铰钢曲杆模型。

工况三：钢曲杆采用等截面H型钢，拱跨长 6 m，矢跨比1/6，其中h为型钢高度，b为型钢宽度，t1为腹板宽度，t2为翼缘宽度，型钢尺寸h×b×t1×t2=100 mm×100 mm×6 mm×8 mm，E1=E2=2.06×108 KN/m²，H型钢截面面积A1=21.9 cm²，钢曲杆在x-x轴的惯性矩Ix=383 cm4，在y-y轴的惯性矩Iy=134 cm4，其余设置同工况一。此工况选用无铰钢曲杆模型。

4　钢曲杆模型建立

运用有限元分析软件，结合具体工程实例，建立不同工况下钢曲杆有限元模型如图1、图2与图3：

图1　工况一模型

图2　工况二模型

图3　工况三模型

5　钢曲杆力学特征数值分析

（1）对模型一与模型二进行热力耦合分析，选取水平距离钢曲杆左端1.5 m、3 m和4.5 m处三个节点，记录不同时间下，模型一与模型二不同节点处竖向位移，绘制成图4：

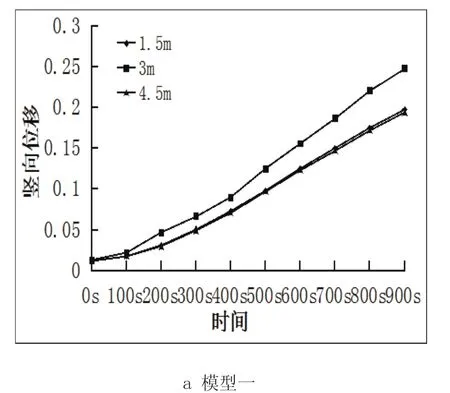
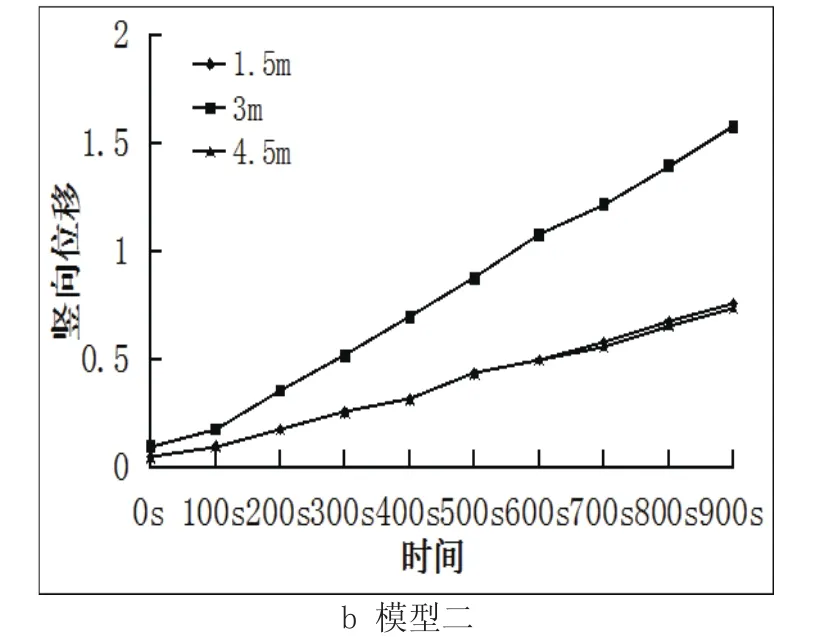
图4　模型一与模型二不同节点处竖向位移随时间变化图（单位：10-5m）

由图4可知：在模型一与模型二中，钢曲杆不同节点处竖向位移随时间变化而改变，并且在节点端点处无位移变形。以跨中为对称点的节点处竖向位移大小近似相等，由于制作不规则、温度不均匀等原因，在合理范围内会存在微小误差。跨中最大高度3米处的竖向位移在不同时间下均为钢曲杆竖向位移变化最大处，可知钢曲杆跨中处于最不稳定位置，在设计时应进行稳定性验算。

（2）记录模型一与模型二在不同时间下不同节点处应变，绘制成表1：

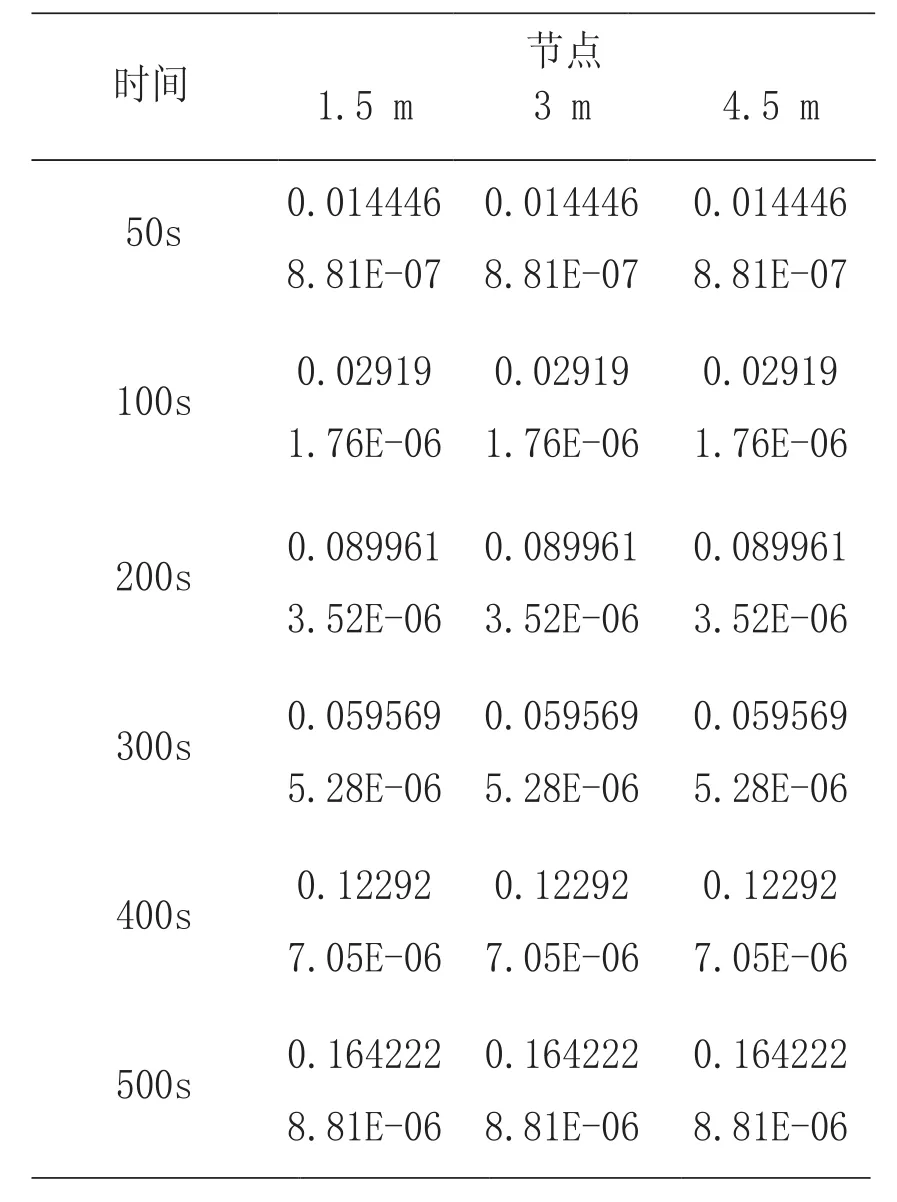
表1　模型一与模型二不同节点处应变随时间变化值（单位：N/mm²）

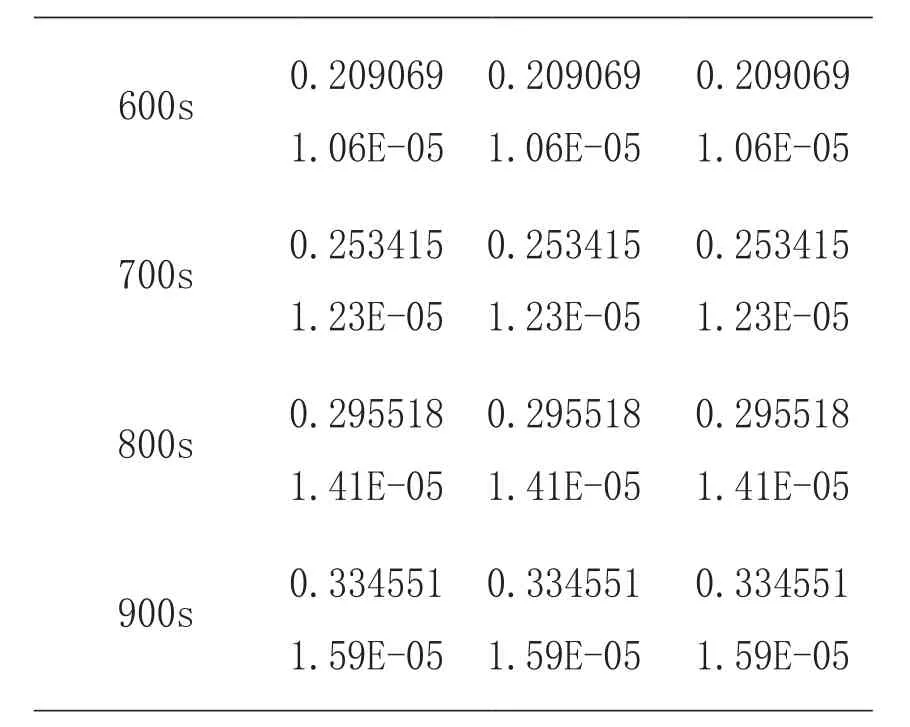
由表1可知，在模型一与模型二中，水平距离钢曲杆左端1.5 m、3 m和4.5 m处节点应变在同一时间下基本相同，同一节点处应变随温度升高而逐渐增大。对比模型一与模型二应变值，模型二应变均小于模型一应变，因此无铰钢曲杆在高温（火灾）环境下比两铰钢曲杆更具稳定性，承载性能更高。

（3）记录模型三钢曲杆跨中截面处上翼缘、腹板与下翼缘处横向竖向位移，绘制成图5：

图5　模型三跨中截面不同位置竖向位移随时间变化图（单位：10-6m）

由图5可知：H型钢截面从上翼缘至下翼缘位移逐渐减小，顶端翼缘处位移位移最大，并且随着温度的升高，中部腹板与底端翼缘位移很小且变化也较小，顶端位移发生很大改变。即H型钢截面钢曲杆在高温（火灾）环境下，顶端翼缘处变形最大，在实际工程中，容易发生破坏，在设计时应进行稳定性验算。

（4）记录不同时间下模型二与模型三不同节点处应变，绘制成表2：

表2　模型二与模型三不同节点处应变随时间变化值（单位：N/mm²）

由表2可知，对比模型二与模型三，不同时间下，模型二不同节点处应变均大于模型三应变，因此，在高温（火灾）环境下，选用H型钢截面钢曲杆较为合理。

6　结论

本文通过应用有限元方法，根据热力耦合分析原理与钢曲杆的力学性质，结合具体工况进行研究分析，得出以下结论：

（1）由模型一与模型二曲杆竖向位移变化可知：在高温（火灾）环境下，钢曲杆跨中竖向位移始终最大，钢曲杆跨中处于最不稳定位置，在设计时应进行稳定性验算。

（2）对比模型一与模型二应变可知：当钢曲杆支座约束不同时，无铰钢曲杆比两铰钢曲杆应变更小，因此无铰钢曲杆承载性能相应较高，结构更安全，更加符合建设要求。

（3）由模型三钢曲杆跨中截面竖向位移可知：在高温（火灾）环境下，H型钢截面钢曲杆顶端翼缘处竖向位移最大，因此处于最不稳定位置，在设计时应进行稳定性验算。

（4）对比模型二与模型三应变可知：当钢曲杆支座约束形式相同，选用H型钢截面比钢管截面的变形要小，H型钢钢曲杆承载性能相应较高。

在钢曲杆结构设计时，选用H型钢截面无铰钢曲杆较为合理，同时应对H型钢截面最薄弱位置（顶端翼缘）加强保护。

［1］郭彦林，窦超.钢拱结构设计理论与我国钢曲杆结构技术规程［J］.steel construction ,2009,24（5）：59.

［2］Thomas I R, Bennetts I D. Development in the design of steel structures for fire［J］. Journal of Constructional Steel Research, 1992, 23（1）：295-312.

［3］Spyros S. Experimental and analytical studies of steel joint components at elevated temperatures［J］.Structure in fire, Sheffield, 2002, 28（2）： 83-94.

［4］European Committee for Standardization. ENV 1993-1-2, Eurocode 3, Design of Steel Structures,Part 1.2： Structural Fire Design［S］.

［5］European Committee for Standardization.ENV 1994-1-2, Eurocode 4, Design of Composite and Concrete Structures, Part 1.2： Structural Fire Design［S］.

［6］李国强.钢结构抗火设计方法的发展［J］. 钢结构，2000（3）： 47-49.

［7］李国强，韩林海，楼国彪，等.钢结构及钢-混凝土组合结构抗火设计［M］.北京：中国建筑工业出版社, 2006.

［8］黄珏倩，李国强.大空间火灾中火焰辐射对钢构件升温的影响［J］.自然灾害学报，2008，17（5）：87.

［9］屈立军，李焕群.Q420钢材高温强度试验研究［J］.消防科学与技术，2004，23（3）： 223-225.

［10］王秀丽，陈志祥.新型加强型钢拱梁的性能分析及优化［J］.建筑科学，2007，23（3）：1-5.

［11］郭彦林，窦超.我国拱形钢结构设计理论研究现状与展望［J］.建筑结构学报，2012，33（7）：1.

［12］孙强.钢结构设计原理［M］.合肥：合肥工业大学出版社，2005.

［13］曾涛，王俊平.浅谈钢拱结构的稳定［J］.山西建筑，2008，34（2）：92-93.

［14］林铃忠，梁书亭.钢管混凝土拱在张弦梁结构中的应用分析［J］.山西建筑，2006,32（18）：5-6.

［15］齐晗兵，王莉莉，卢丽冰.火灾条件下钢结构温度场模拟［J］.油气田地面工程，2005,24（5）：15.

［16］贾宝荣，李晓东.不同跨受火时两层两跨钢框架火灾行为试验［J］.哈尔滨工业大学学报，2008,40（12）：24-28.

The numerical analysis of the mechanical characteristics of steel curved bar under the environment of high temperature （fire）

ZHAO Xiongfu,SUN Qiang,GUO Wei
（School of Civil Engineering,Anhui JianZhu University, Hefei, 230601 ）

Under the environment of high temperature（fre）, the stress and deformation of steel curved bar（SCB）will be greatly changed, as well as its mechanical characteristics in the SCB structure . On the basis of the theory of structural stability and thermodynamics principle, we combine with three different conditions and discussthe infuence that factors such asdifferent support formsunder high temperature （fre）and the cross section forms etc may haveon the mechanical characteristics of steel bars . Thenthe mechanical characteristics of steel bars under three conditions have been discussed and analyzed by applying the fnite element method.Then it is concluded that the H type steel section inarticulata curved rod is more in line with the requirements ofthe construction safety and the results will be valuable for study of the fre resistance of SCB.

Steel curved bar；high temperature （fre）；mechanical characteristics；fnite element；numerical analysis

TU391

A

2095-8382（2016）04-017-05

10.11921/j.issn.2095-8382.20160404

2015-11-06

国家重点基础研究发展计划项目（2012CB719703）, 安徽高校省级自然科学研究重大项目（KJ2014ZD06），安徽省自然科学基金（1408085QE96）。

赵雄夫（1991-），男，硕士生，主要研究方向为钢结构设计理论与应用。