基于方位空变斜距模型的大斜视机动平台波数域SAR成像算法

董 祺 杨泽民 李震宇 孙光才 邢孟道



基于方位空变斜距模型的大斜视机动平台波数域SAR成像算法

董 祺*①②杨泽民③李震宇①②孙光才①②邢孟道①②

①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)②(西安电子科技大学信息感知技术协同创新中心 西安 710071)③(中国电子科技集团第二十九研究所 成都 610036)

由于加速度的存在，非线性轨迹的大斜视机动平台的SAR成像是一个亟待研究的问题。传统的斜距模型一般没有考虑加速度带来的点目标方位空变，在加速度存在的情况下难以获得良好的聚焦效果。为了解决加速度带来的影响，该文提出一种带加速度的非线性轨迹的方位空变模型，在此基础上提出一种大斜视波数域成像算法，通过空变滤波函数去除加速度带来的方位调频率变化和多普勒中心空变。最后通过误差分析证明了所提方位空变模型的有效性，并通过仿真对比实验结果证明了所提成像算法的有效性。

合成孔径雷达；大斜视；方位空变；斜距模型

1 引言

合成孔径雷达由于其全天时全天候高分辨远距离的特性，被广泛应用于军事和民用领域，用于地形测绘、交通疏导、军事侦察及打击。近年来，合成孔径雷达开始逐渐应用于高速机动平台[1,2]，用来为导航控制提供信息。高速机动平台一般采用大斜视工作模式进行成像，以确保有足够的时间调整飞行姿态和轨迹[3,4]。

导弹在飞行过程中，为避免拦截，往往采用不规则飞行轨迹，其运行速度和加速度的大小和指向一直处于变化之中，这使得雷达工作模型较为复杂，且往往不满足方位平移不变性，因而常规频域算法难以获得大范围的聚焦图像。

距离-多普勒算法由于忽略了距离向的距离弯曲差，在正侧视和小斜视角情况近似较为精确，在大斜视模式下成像会产生明显散焦[5]；改进的非线性CS算法充分考虑了沿场景纵深的距离弯曲的空变性，能应用于较大的斜视角，能对较大斜视角的SAR数据进行高分辨成像，但在前斜视情况下不再适用[6,7]。一些利用级数反演方法的成像算法，一般采用四阶斜距模型，通过推导信号2维频谱构造2维的匹配函数，但只能适用于较小的场景，难以用于大场景的高分辨成像。BP算法是一种理论上无近似的时域成像算法[11]，可以用于任何已知轨迹的SAR成像，无需进行任何模型近似，可以获得高质量图像。但在投影过程中，对所有的成像点，都需要逐次回波进行斜距的计算，需要消耗较多处理时间，FBP[12]及FFBP[13]算法等典型的改进BP算法，在一定程度上提升了运算效率，但相对于频域算法，依旧具有较大的运算负担。类似于时域成像算法，波数域算法[14]能够不加近似地实现聚焦，对于其插值带来的较大运算量，通过NUFFT’s(Non-Uniform Fast Fourier Transforms)[15]以及无插值方式[16]快速实现。文献[17-19]提出的斜视SAR俯冲成像的Omega-K算法，首先将斜距模型近似转化为标准Omega-K算法中的斜距形式，再进行成像，其不足之处在于忽略了回波信号沿方位的空变性。

针对以上问题，本文提出一种基于方位空变斜距模型的大斜视机动平台波数域成像算法，首先分析了加速度存在条件下的斜距模型，通过对其空变性进行分析，提出了方位空变补偿函数，再对加速度引起的相位的高阶调制进行补偿，即可用传统Omega-K算法实现聚焦。最后通过点目标仿真实验验证了本文算法的有效性。

2 方位空变斜距模型与等效匀速直线模型

弹载SAR系统为保证时效性，往往采用较短的合成孔径，以实现导弹姿态的实时调整，在一次合成孔径时间内导弹的飞行可近似为匀加速运动，即短时间内加速度的大小和指向认为不变[18]，图1的俯冲SAR成像几何模型基于匀加速直线模型，本文的讨论均基于该模型。如图1所示，导弹的初始速度为，指向方向，加速度与速度的夹角为，这里需要说明的是，加速度是3维矢量，但其垂直于成像斜平面的分量在短合成孔径时间内对相位的影响微乎其微，因此本文只讨论加速度在斜平面的分量对成像的影响，默认为加速度与速度的夹角在斜平面的投影，加速度的垂直分量对相位的影响将在文末给出。雷达前斜视角为，导弹飞行轨迹如图中的实曲线所示。点为场景中任意点，为方位慢时间，点多普勒中心时刻为,为多普勒中心时刻目标与雷达的斜距，则点的瞬时斜距可表示为

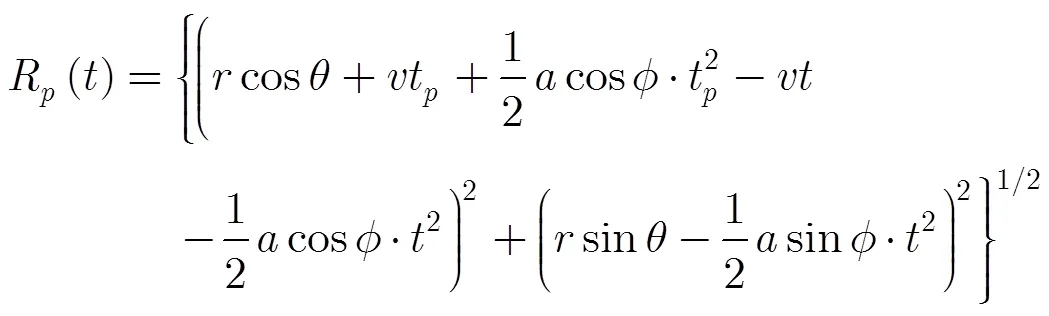
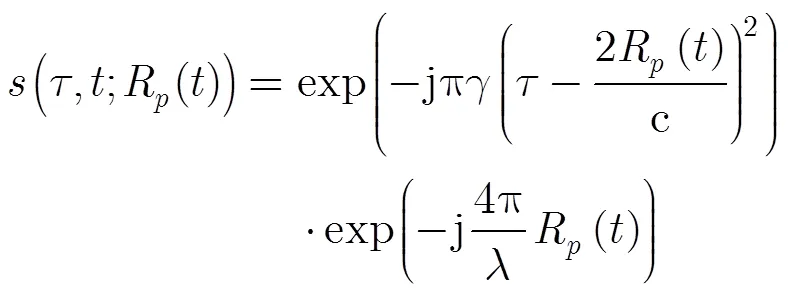
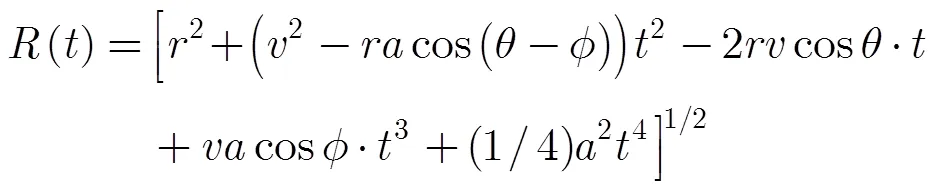
文献[17]针对式(3)所示的匀加速弹载大斜视SAR模型提出了一种等效匀速模型，首先将式(3)进行泰勒展开，先将慢时间的高次项(三阶以上)进行补偿，然后通过一组变量替换：和，则式(3)可简化为

(4)

此时匀加速模型已近似为匀速模型，采用常规Omega-K算法即可成像。该模型忽略了斜距历程的方位空变，即认为，因此该模型针对小场景有效，当场景方位尺寸较大时，该模型可能失效。同时，当加速度较大、前斜视角较小时，可能导致，此时，等效斜视角为复数，甚至,也为复数，该方法在这种情况下并不适用。

3 方位空变斜距模型与等效匀速直线模型

将式(5)泰勒展开，可得

(7)

首先构造距离匹配滤波函数进行距离脉冲压缩，

距离脉冲压缩后，将式(6)代入式(7)，式(7)可表示为

(9)

其中，第1项表征加速度对方位调频率的调制，第2项表征加速度引入的多普勒中心空变，第3项为定值，不影响聚焦。构造空变滤波函数

(11)

即可同时补偿加速度对方位调频率的影响以及多普勒中心空变。该过程可用图2所示的时频图形象表示。图2中忽略了加速度对相位的高阶调制。图中轴表示多普勒频率轴，指多普勒中心。假设场景中沿导弹飞行方向不同方位位置有3个点目标，假设雷达波束指向不变，图2(a)分别画出了3个点的时频线。图中表示出了受加速度的调制，3个点目标的多普勒中心频率存在空变。

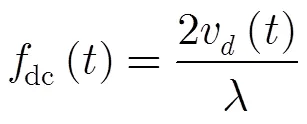
其中，

(13)

图2 加速度二阶调制相位的补偿

弹载前斜视SAR处理往往采用较短的合成孔径快速处理，在短时间内，加速度对相位的调制主要集中在二阶，因此图2没有示意加速度高阶调制相位，若全面考虑加速度的影响，那么信号已非线性调制，此时应补偿加速度对相位的高阶调制，补偿函数为

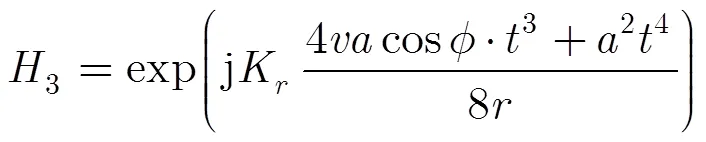
在短合成孔径时间内，经过对加速度调制相位的补偿后，导弹可看作匀速直线飞行，此时可采用Omega-K算法进行处理。利用驻相点法将回波做方位傅里叶变换变到2维频域，信号表达式为

(15)

(17)

再利用Stolt插值消除式(17)中二阶以上的残余相位调制，完成残余距离徙动矫正(Range Cell Migration Correction, RCMC)、残余二次距离压缩(Second Range Compresstion, SRC)和方位压缩，信号可表示为

图3 算法流程图

4 加速度的垂直分量对相位的影响

以上讨论默认加速度方向在斜平面内，而实际中导弹的加速度可能指向任意方向，因此需要分析加速度在斜平面法线方向的投影分量对成像的影响。图4是含有3维加速度的弹载SAR系统瞬时斜距示意图，图中为瞬时斜距在斜平面的投影，为在法线方向的投影分量。

(20)

图4 加速度斜平面法线方向分量斜距贡献示意图

5 仿真实验

5.1 系统建模精度分析

本文讨论均基于式(6)所描述的模型，如前文所述，该模型忽略了斜距历程的方位高次空变，下面通过数值分析验证其在短合成孔径时间下的合理性。假设雷达平台以1000 m/s的初始速度和10 m/s2的加速度向前飞行，加速度与初始速度的夹角为30°，前斜视角为10°，雷达合成孔径时间为0.2 s，作用距离为20 km。

利用MATLAB计算式(1)和式(6)的差，转换成相位(波长为0.018 m)，计算结果如图5所示。图5为慢时间高次项随方位的空变性对相位误差造成的影响，从图中可以看出，在2 km的范围内相位误差未超过，其影响可忽略。

5.2 成像仿真实验

为验证本文方法的有效性，下面用一组弹载前斜视仿真数据进行成像处理，并将处理结果与文献[19]提出的CA-Omega-K算法处理结果进行对比。系统主要仿真参数如表1所示，其中部分参数与5.1节中实验一致，而前斜视角采用45°是为了避免CA-Omega-K算法中等效速度和等效角度出现复数的情况。雷达工作在Ku波段，以8192 Hz的脉冲重复频率(Pulse Repeat Frequency, PRF)在0.25 s时间内收发了2048次脉冲。

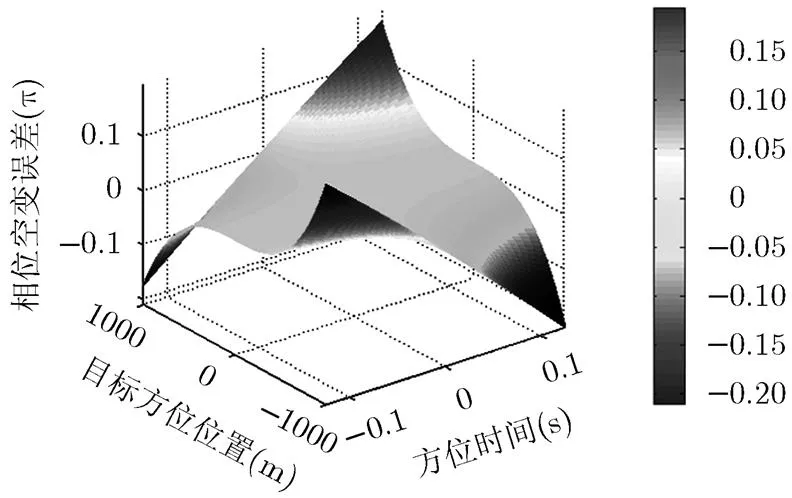
图5 相位误差方位空变分析

表1 系统部分仿真参数

载频16.5 GHz 发射信号带宽75 MHz 采样频率90 MHz 合成孔径时间1 s 下视角60° 导弹初始速度1 km/s 加速度10 m/s2 轨道高度8.66 km 脉冲持续时间3 μs PRF8192 Hz 场景大小4 km×4 km 前斜视角45° 作用距离20 km 加速度与初始速度夹角30°

场景中放置9个点目标，以1000 m间隔均匀分布，如图6所示。分别使用本文算法和CA- Omega-K算法处理回波数据，~点的成像结果分别如图7，图8所示，其中图7为本文算法成像结果，图8为CA-Omega-K算法成像结果，每个点的横向为方位向，纵向为距离向。图7为对点目标的方位向和距离向进行64倍插值的结果，图8同样为对点目标的方位向和距离向进行64倍插值的结果，并对方位向进行了四视处理。需要说明的是，本文算法通过补偿加速度对调频率的调制，导弹可认为匀速飞行，那么系统方位维分辨率为，其中为多普勒调频率，为合成孔径时间，方位分辨率为1.54 m。系统距离维分辨率为1.77 m，其中为光速，为信号带宽。对于CA-Omega-K算法来说，距离维分辨率与本文算法相同，但由于等效速度和等效前斜视角不同于初始速度和初始前斜视角，在本实验中其方位分辨率只有6.57 m。

从图7和图8中可以看出，本文算法的成像质量明显优于CA-Omega-K算法的成像质量，这是由于本文算法对加速度进行了一定的补偿，补偿后平台的不规则飞行过程可近似为一个恒速的飞行过程。对于CA-Omega-K算法而言，中心点可以得到聚焦良好的图像，但远离中心的边缘点的成像质量恶化的较为明显。为了进一步展示本文算法的优势，图9给出了对于同一块场景，两种算法所得成像结果的方位向的峰值旁瓣比以及积分旁瓣比。图9(a)和图9(b)分别表示的是随着目标点偏离场景中心的距离变大，方位向峰值旁瓣比和积分旁瓣比的变化曲线，图9(c)和图9(d)分别表示的是随着目标点偏离场景中心的距离变大，距离向峰值旁瓣比和积分旁瓣比的变化曲线。横坐标1~8表示的是距离场景中心点由近到远的8个点目标，相邻两点之间距离为400 m，即图9定量表示了场景宽度为6400 m时的聚焦效果。当点目标距离中心点越来越远时，从图9(a)和图9(b)中可以看出，本文算法得到的点目标方位向的峰值旁瓣比和积分旁瓣比明显优于CA-Omega-K算法得到的结果，而从图9(c)和图9(d)中可以看出，两种算法得到的距离向聚焦结果没有明显差别。这是由于本文算法是针对加速度造成的方位空变性进行了一定补偿，并没有对距离向的成像进行改进。以上所有仿真实验均说明了本文算法在处理带加速度的大斜视机动平台SAR成像中的优势。

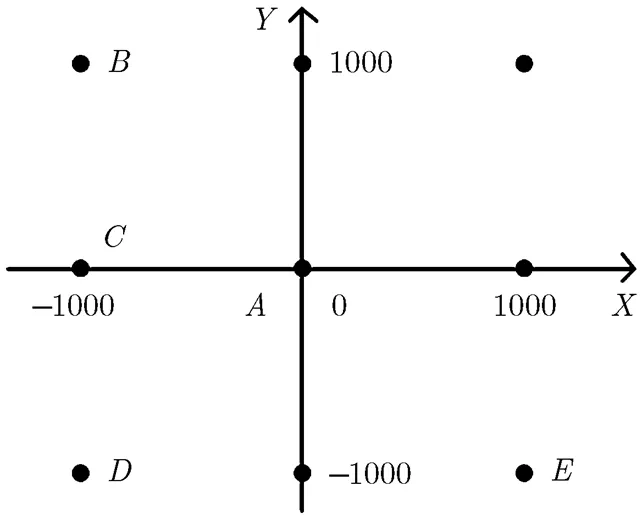
图6 点目标分布

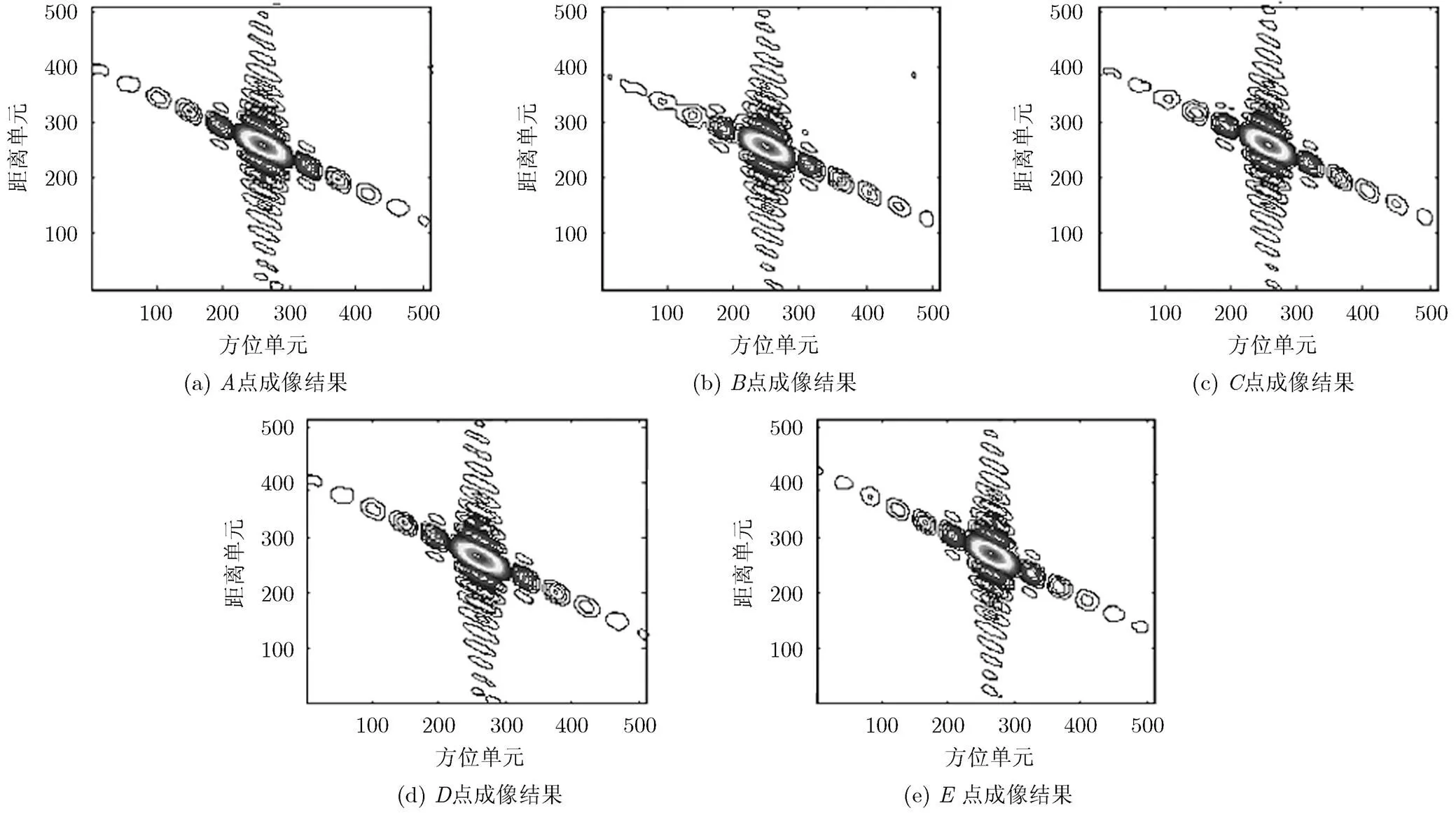
图7 本文算法成像结果

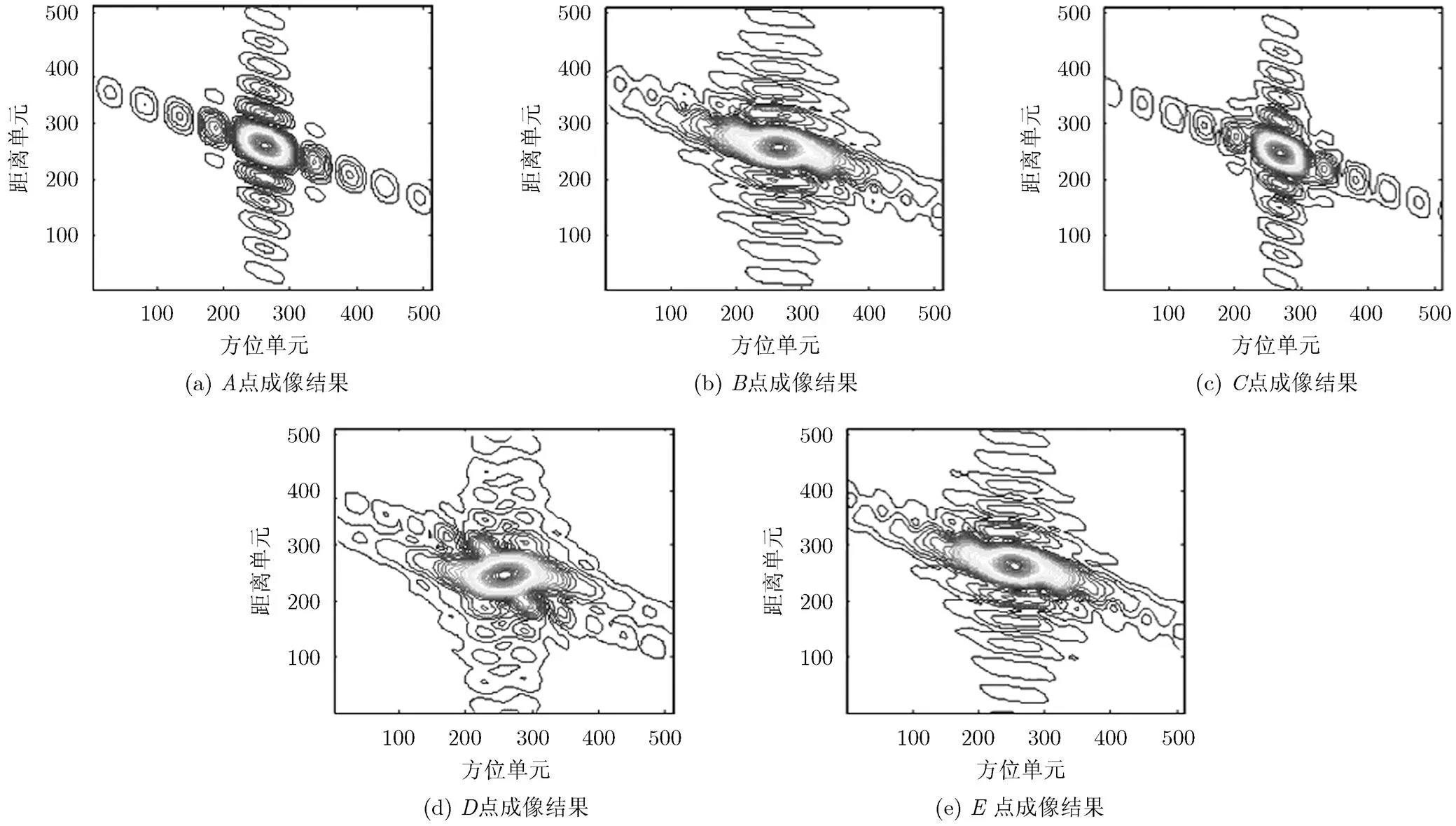
图8 CA-Omega-K算法成像结果

图9 成像质量对比

6 结论

本文提出了一种基于方位空变斜距模型的大斜视机动平台波数域成像算法，该算法利用短合成孔径时间内，机动平台的加速度可近似恒定的性质，提出了一种加速度存在下的方位空变斜距模型，通过对斜距模型进行合理的简化，以及对简化后各个相位项的分析，提出了去方位空变滤波函数，能够去除加速度带来的调频率影响以及成像点沿方位向的时延。该方法较之未考虑方位空变的恒加速算法，如CA-Omega-K算法，能适用于更大的场景，取得更为优质的聚焦效果。模型简化误差的理论分析和仿真实验均证实了本文算法在成像质量上的优势。

参考文献

[1] ZHANG Lei, SHENG Jialian, XING Mengdao,. Wavenumber-domain autofocusing for highly squinted UAV SAR imagery[J]., 2012, 12(5): 1574-1588. doi: 10.1109/JSEN.2011.2175216.

[2] ZHANG Lei, QIAO Zhijun, XING Mengdao,A robust motion compensation approach for UAV SAR imagery[J].,2012, 50(8): 3202-3218. doi: 10.1109/TGRS.2011.2180392.

[3] 李震宇, 梁毅, 邢孟道, 等. 一种俯冲段子孔径SAR大斜视成像及几何校正方法[J]. 电子与信息学报, 2015, 37(8): 1814-1820. doi: 10.11999/JEIT141516.

LI Zhenyu, LIANG Yi, XING Mengdao,New subaperture imaging algorithm and geometric correction method for high squint diving SAR based on equivalent squint model[J].&, 2015, 37(8): 1814-1820. doi: 10.11999/ JEIT141516.

[4] 李震宇, 梁毅, 邢孟道, 等. 一种大斜视 SAR 俯冲段频域相位滤波成像算法[J]. 电子学报, 2015, 43(10): 2014-2021. doi: 10.3969/j.issn.0372-2112.2015.10.020.

LI Zhenyu, LIANG Yi, XING Mengdao,A frequency phase filtering imaging algorithm for high squint SAR in diving movement[J]., 2015, 43(10): 2014-2021. doi: 10.3969/j.issn.0372-2112.2015.10.020.

[5] XIAO Jing and HU Xuecheng. A modified RD algorithm for airborne high squint mode SAR imaging[C]. IEEE 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 2007: 444-448.doi: 10.1109/APSAR. 2007.4418646.

[6] 周松, 周鹏, 李亚超, 等. 弹载SAR下降段成像算法研究[J]. 西安电子科技大学学报自然科学版, 2011, 38(3): 90-98. doi: 10.3969/j.issn.1001-2400.2011.03.015.

ZHOU Song, ZHOU Peng, LI Yachao,. Research on the imaging algorithm for missile-borne SAR with downward movement[J].(), 2011, 38(3): 90-98.

[7] CHEN Si, ZHANG Shuning, ZHAO Huichang,A new Chirp scaling algorithm for highly squinted missile-borne SAR based on FrFT[J].&, 2015, 8(8): 3977-3987. doi: 10.1109/JSTARS.2014.2360192.

[8] 周鹏, 周松, 熊涛, 等. 基于级数反演的弹载 SAR 下降段CZT 成像算法[J]. 电子与信息学报, 2010, 32(12): 2861-2867. doi: 10.3724/SP.J.1146.2010.00452.

ZHOU Peng, ZHOU Song, XIONG Tao,A Chirp-Z imaging algorithm for missile-borne SAR with diving maneuver based on the method of series reversion[J].&, 2010, 32(12): 2861-2867. doi: 10.3724/SP.J.1146.2010.00452.

[9] 周松, 包敏, 周鹏, 等. 基于方位非线性变标的弹载 SAR 下降段成像算法[J]. 电子与信息学报, 2011, 33(6): 1420-1426. doi: 10.3724/SP.J.1146.2010.01124.

ZHOU Song, BAO Min, ZHOU Peng,Imaging algorithm for missile-borne SAR with downward movement based on azimuth nonlinear chirp scaling[J].&, 2011, 33(6): 1420-1426. doi: 10.3724/SP.J.1146.2010.01124.

[10] LI Zhenyu and XING Mengdao. A frequency-domain imaging algorithm for highly squinted SAR mounted on maneuvering platforms with nonlinear trajectory[J]., 2016, 54(7): 4023-4038. doi: 10.1109/TGRS.2016.2535391.

[11] DAVID C, MUNSON J R, JENKINS W K,. A tomographic formulation of spotlight mode synthetic aperture radar[J]., 1983, 72(8): 917-925.doi10.1109/PROC.1983.12698.

[12] YEGULALP A F. Fast back-projection algorithm for synthetic aperture radar[C]. The Record of the 1999 IEEE Radar Conference, Waltham, MA, USA, 1999: 60-65.

[13] ULANDER L M H, HELLSTEN H, and STENSTROM G. Synthetic-aperture radar processing using fast factorized back-projection[J]., 2003, 39(3): 760-776.doi10.1109/TAES. 2003.1238734.

[14] REIGBER A, ALIVIZATOS E, POTSIS A,Extended wavenumber-domain synthetic aperture radar focusing with integrated motion compensation[J].-,ation, 2006, 153(3): 301–310. doi: 10.1049/ ip-rsn:20045087.

[15] WU Yong, SONG Hongjun, SHANG Xiuqin,Improved RMA based on nonuniform fast Fourier transforms[C]. 9th International Conference on Signal Processing, Beijing, China, 2008: 2489-2492. doi: 10.1109/ICOSP.2008.4697654.

[16] LI Zhe, WANG Jian, and LIU Qinghuo. Interpolation-free Stolt mapping for SAR imaging[J]., 2014, 11(5): 926-930. doi: 10.1109/ LGRS.2013.2281847.

[17] LI Zhenyu, LIANG Yi, XING Mengdao,An improved range model and omega-K-based imaging algorithm for high- squint SAR with curved trajectory and constant acceleration [J]., 2016, 13(5): 656-660. doi: 10.1109/LGRS.2016.2533631.

[18] TANG Shiyang, ZHANG Linrang, GUO Ping,Acceleration model analyses and imaging algorithm for highly squinted airborne spotlight-mode SAR with maneuvers[J].&, 2015, 8(3): 1120-1131. doi: 10.1109/JSTARS.2015.2399103.

[19] TANG Shiyang, ZHANG Linrang, GUO Ping,An omega-K algorithm for highly squinted missile-borne SAR with constant acceleration[J]., 2014, 11(9): 1569-1573. doi: 10.1109/LGRS. 2014.2301718.

董 祺： 女，1991年生，博士生，研究方向为机载SAR成像算法等.

杨泽民： 男，1988年生，博士生，研究方向为机载SAR运动补偿、星载SAR成像算法研究等.

李震宇： 男，1991年生，博士生，研究方向为机载SAR运动补偿及成像和弹载SAR成像算法研究等.

孙光才： 男，1984年生，副教授，研究方向为星载高分辨多模式SAR成像算法与动目标成像和干扰抑制等.

邢孟道： 男，1975年生，教授，博士生导师，研究方向为SAR、ISAR成像算法与动目标识别等.

Wavenumber-domain Imaging Algorithm for High Squint SAR Based on Azimuth Variation Range Model

DONG Qi①②YANG Zemin③LI Zhenyu①②SUN Guangcai①②XING Mengdao①②

①(,,,710071,)②(,,,710071,)③(29,610036,)

Due to the acceleration in the moving of the platform, the SAR imaging of highly squinted maneuvering platform becomes a problem to be solved urgently. The majority of currently existing range models fail in taking the azimuth-variation into consideration, so the well-focused images are not obtained. To solve these problems, a new azimuth-variation range model under the non-linear trajectory caused by acceleration is constructed. Based on this model, a wavenumber-domain imaging algorithm for high squint SAR is proposed, which takes advantage of the azimuth-variation filter to remove the azimuth chirp rate changes and Doppler center changes caused by the acceleration. By the analysis of the model error, the precision of the model is confirmed. Contrast simulation results are presented to valid the superiority of the proposed approach.

Synthetic Aperture Radar (SAR); High squint; Azimuth variation; Range model

TN957.52

A

1009-5896(2016)12-3166-08

10.11999/JEIT160785

2016-07-22；改回日期：2016-11-24；

2016-12-13

董祺 dq544120925@126.com

国家自然科学基金(61301292)，空间测控通信创新探索基金(201509A)

The National Natural Science Foundation of China (61301292), The AeroSpace T.T.& C. Innovation Program (201509A)