可提取衍生目标的带标签GM-PHD算法

陈金广，赵甜甜，马丽丽，徐步高,2



可提取衍生目标的带标签GM-PHD算法

陈金广1，赵甜甜1，马丽丽1，徐步高1,2

( 1. 西安工程大学计算机科学学院，西安 710048;2. 德克萨斯州大学奥斯汀分校人类生态系, 德克萨斯州奥斯汀 78712 )

针对带标签的高斯混合概率假设密度滤波算法无法获取衍生目标的问题，提出一种可以提取衍生目标的带标签GM-PHD算法。首先，通过为高斯项加注标签的方式区别不同的目标，以辨别单个目标及其航迹。其次，在滤波过程中，对每一时刻得到的状态估计值与已形成的航迹标签进行匹配关联，实现航迹维持。最后，通过设置衍生阈值来判断状态估计中是否存在衍生目标以及可能产生的目标个数，为新生目标高斯项和可能的衍生目标高斯项重新分配标签，并创建新的航迹。仿真实验结果表明，与传统的带标签GM-PHD算法相比，在衍生目标存在的情况下，改进算法具有更好的跟踪性能。

概率假设密度滤波；随机有限集；状态估计；衍生目标；带标签GM-PHD

0 引 言

20世纪中后期，多目标跟踪问题的研究得到诸多学者的关注，根据是否对数据进行关联可将多目标跟踪算法分为两类，一类是以数据关联为基础的传统多目标跟踪算法，如联合数据关联(JPDA)[1]、多假设跟踪(MHT)[2]；另一类是基于有限统计学理论的概率假设密度(PHD)滤波算法[3]。Vo提出的非线性系统下的序贯蒙特卡罗-概率假设密度(SMC-PHD)滤波[4]以及线性系统下的高斯混合概率假设密度(GM-PHD)滤波[5]，解决了PHD滤波器中多重积分计算复杂的问题。PHD滤波算法避免了多目标跟踪系统中因数据关联导致的计算量大的问题，并已运用到多个领域[6-7]。

由于PHD滤波算法主要思想是将多目标状态和量测作为随机集来处理[8]，而随机集中元素的位置和个数是未知且时变的，因此无法得知当前时刻所估计的状态属于哪条航迹。为了解决该问题，有学者提出在PHD框架下获得目标航迹的方法，大致可分为两类，一类是对PHD滤波结果使用传统的数据关联方法以得到航迹，例如文献[9-10]。另一类是通过为粒子或高斯项加标签的方式来实现航迹的获取，如文献[11-12]是对高斯项添加标签，文献[13-14]对粒子加标签得到航迹信息，文献[15]通过对带标签的GM-PHD算法进行改进实现目标交叉情况下的航迹准确估计。

在上述带标签GM-PHD算法中，通常假定衍生目标不存在或者忽视衍生目标的产生，然而，实际应用中常常存在衍生目标不能被忽视的场景，如多弹头导弹、飞行中的飞机发射炮弹等，因此本文提出可提取衍生目标的带标签高斯混合概率假设密度滤波算法。通过修改文献[12]中的标签管理机制以得到衍生目标存在情况下的目标状态估计和航迹维持。仿真实验结果表明了改进算法的优越性，并且更具有一般性。

1 基于随机有限集的多目标跟踪模型

多目标跟踪问题中，使用有限集统计学理论可以将多目标的状态模型和观测模型表示为随机有限集(RFS)形式。时刻多目标状态集合表示为，量测集合为。和分别表示状态空间与量测空间上所有有限子集的集合，和分别表示时刻目标数与量测数。

同样时刻的量测随机集可表示为

2 带标签的GM-PHD算法

带标签的GM-PHD算法是在标准GM-PHDF基础上，为每个高斯项添加标签信息，通过管理标签实现对不同时刻目标状态之间的关联，达到目标航迹估计的目的。

文献[12]使用树形结构来说明标签的演变过程。在航迹初始阶段，为每个高斯项分配独特的标签，并将高斯项状态作为标签树的根节点，此时的标签树是临时航迹树，若标签树上至少有一个分支有状态估计值，则该标签树被认为是确定航迹树。每棵树表示一个目标的航迹，是该航迹初始时刻，所有树的集合就是目标的航迹。若确定航迹树在当前时刻没有状态估计值，则使用预测值为该航迹弥补状态信息，这样在一定程度上避免了因漏检而导致的航迹信息缺失问题。

具体算法过程如下，首先进行初始化，在=0时刻，强度函数和标签集合表示为：

预测：时刻的预测强度函数和预测标签集合表示如下：

裁剪与合并：使用文献[5]的裁剪合并方法对更新后的高斯项进行处理。

状态估计：提取的状态集和标签集如下：

标签管理及航迹关联：通过下面三个步骤对高斯项及其标签进行管理，得到确定的目标航迹。

1) 对得到的目标估计状态进行裁剪，保证每一个标签只保留最大权值高斯项，其余丢弃。

3 可提取衍生目标的带标签GM-PHD算法

目标新生和消亡的随机性是多目标跟踪问题的一个难点，新生目标主要包括自主产生的新生目标和衍生目标。由于衍生目标是已有目标在某时刻产生的额外目标，因此衍生目标产生时具有与存在目标相同的属性，在衍生目标刚产生的一段时间内，状态和运动轨迹可能会与产生它的目标相同。因此对衍生目标的识别和跟踪是很必要的。

在文献[12]的标签管理机制中，因为衍生目标的状态信息会因与产生它的已有目标属于同一标签树而被舍去，导致目标状态估计误差较大，因此本文提出对标签管理机制的改进。在改进算法的标签管理中，为潜在的衍生目标高斯项分配新的标签，避免与已有目标标签重复，以实现对衍生目标的状态和航迹的估计。改进算法的标签管理和航迹关联过程如下：

4 仿真实验与结果分析

从图1可以得到这样的信息：从目标3衍生后，带标签的GM-PHD算法会产生漏估计，即对目标1和目标3的状态估计不能同时进行，而本文改进算法有效地解决了该问题。从图2中可以看出带标签GM-PHD算法对目标数目的估计比标准GM-PHDF更稳定，更准确，但是当衍生目标3出现后，由于带标签GM-PHD算法假设衍生目标不存在，从而导致了目标个数的漏估计。改进算法在存在衍生目标的多目标跟踪系统中，不会像传统算法一样对目标数目的估计出现较大误差。

图3给出了改进算法与标准GM-PHD算法以及传统的带标签GM-PHD算法经过50次蒙特卡洛仿真实验的OSPA误差距离均值。由于在标准GM-PHD算法中，每一时刻新生目标的权值较小，因此提取出状态信息需要一些时间，故前5个时刻的OSPA误差距离为最大值。从图3中可以看出在衍生目标出现(第66时刻)之前三种算法的性能都比较好，但是在衍生目标出现后，改进算法性能比其他两种算法要好。

图1 目标运动轨迹与算法估计

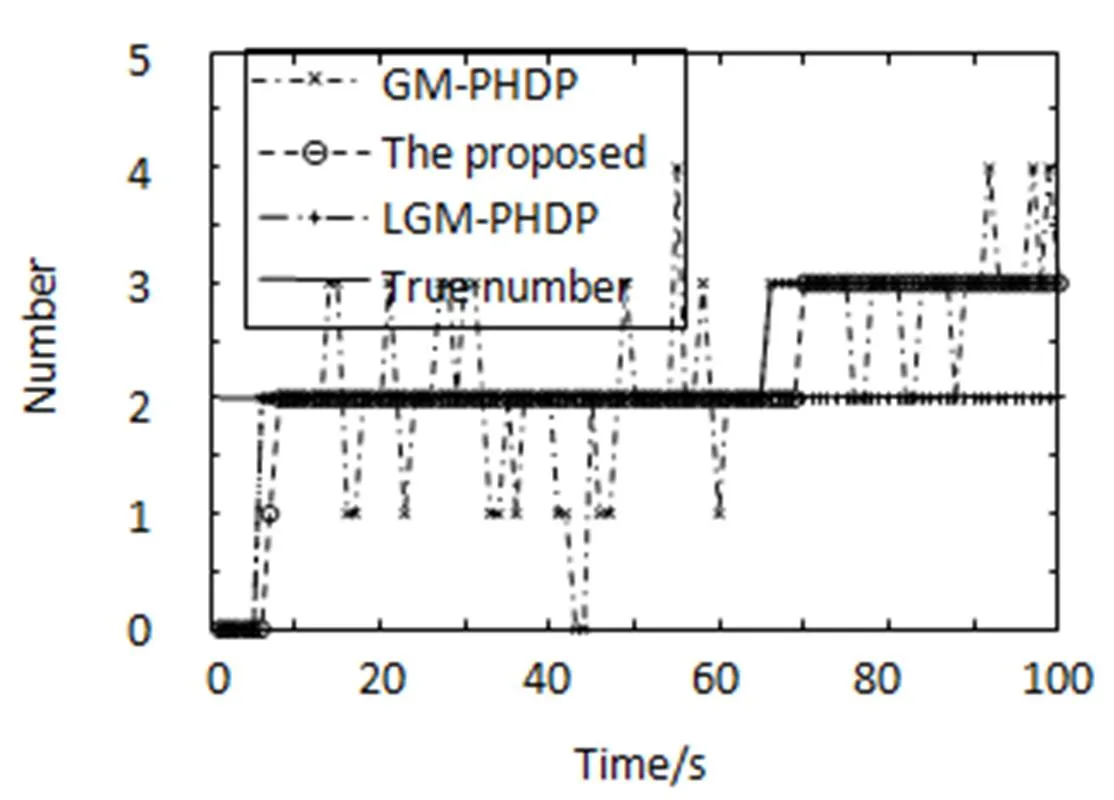
图2 目标数目估计

图3 OSPA距离

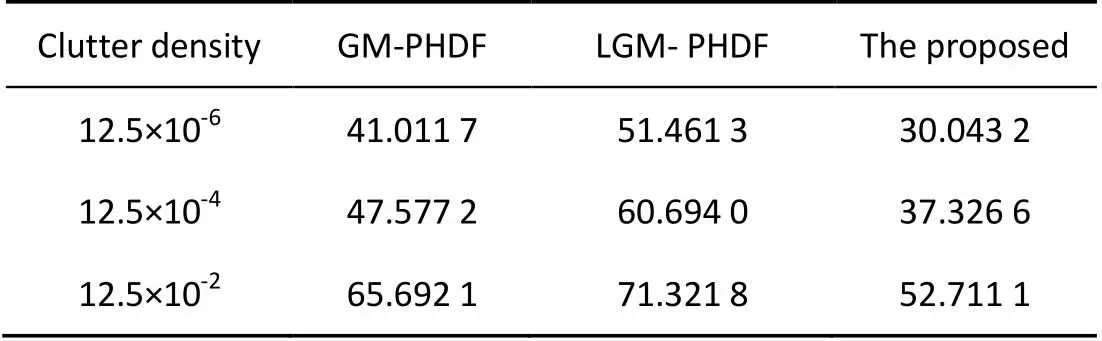
表1 不同杂波密度下的算法性能比较

为了更好的说明算法鲁棒性，在不同杂波密度下对三种算法进行20次蒙特卡洛仿真实验，计算OSPA距离平均值(见表1)。由结果可知，虽然随着杂波密度增加改进算法的状态估计准确性降低，但是与其他两种算法相比仍具有较大的优势。

结束语

本文的贡献在于通过修正标签的管理机制保留衍生目标高斯项信息，并进行航迹关联得到单个目标航迹，使得带标签GM-PHD算法可以较好地处理跟踪过程中出现的目标衍生问题。仿真实验结果表明，改进算法相对传统带标签GM-PHD算法在衍生目标存在情况下具有较好的跟踪性能，且从理论上讲更适用于一般情况。该改进算法的缺点是当杂波密集时，由杂波产生的虚假量测更新得到的高斯项权值较大，可能会被当作衍生目标进行处理，从而导致目标数目的过估计问题。

[1] Blackman S. Multiple hypothesis tracking for multiple target tracking [J]. IEEE Aerospace and Electronic Systems Magazine(S0885-8985)，2004，19(1)：5-18.

[2] Yaakov B S，Peter K W，TIAN Xin. Tracking and Data Fusion：a handbook of algorithms [M]. Storrs：YBS Publishing，2012：125-139.

[3] Mahler Ronald P S. Multitarget bayes filtering via first-order multitarget moments [J]. IEEE Transactions on Aerospace and Electronic Systems(S0018-9251)，2003，39(4)：1152-1178.

[4] Vo Ba Ngu，Singh Sumeetpal，Doucet Arnaud. Sequential Monte Carlo methods for multi-target filtering with random finite [J]. IEEE Transactions on Aerospace and Electronic Systems(S0018-9251)，2005，41(4)：1224-1244.

[5] Vo Ba Ngu，MA Wing Kin. The Gaussian mixture probability hypothesis density filter [J]. IEEE Transactions on Signal Processing(S1053-587X)，2006，54(11)：409-4104.

[6] Frencl V B，do Val J B R. State estimation using GM-PHD filter applied to tracking of individuals [C]// IEEE Radar Conference，Ottawa，Canada，April 29-May 3，2013，13：1-6.

[7] Ramona Georgescu，Peter Willett. The GM-CPHD tracker applied to real and realistic multistatic sonar data sets [J]. IEEE Journal of Oceanic Engineering(S0364-9059)，2012，37(2)：220-235.

[8] Mahler R. A theoretical foundation for the Stein-Winter probability hypothesis density (PHD) multi-target tracking approach [C]// Proceedings of the MSS National Symposium on Sensor and Data Fusion，San Antonio，TX，2000：99-117.

[9] LAI Lin，YAAKOV Bar Shalom，THIA Kirubarajian. Track labeling and PHD filter for multitarget tracking [J]. IEEE Transactions on Aerospace and Electronic Systems(S0018-9251)，2006，42(3)：778-795.

[10] Panta K，Vo Ba Ngu，Singh Sumeetpal. Probability hypothesis density filter versus multiple hypothesis tracking [J]. Proceedings of SPIE(S0277-786X)，2004，5249：284-295.

[11] Clark D，Panta K，Vo Ba Ngu. The GM-PHD filter multiple target tracker [C]// Proceedings of the 9th International Conference on Information Fusion，Florence，Italy，July 10-13，2006：1-8.

[12] Panta Kusha，Clark Daniel E，Vo Ba Ngu. Data association and track Management for Gaussian Mixture Probability Hypothesis Density Filter [J]. IEEE Transactions on Aerospace and Electronic Systems(S0018-9251)，2009，45(3)：1003-1016.

[13] ZHU Hongyan，HAN Chongzhao，LIN Yan. Particle labeling PHD filter for multi-target track-valued estimates [C]// Proceedings of the 14th International Conference on Information Fusion，Chicago，USA，July 5-8，2011：1-8.

[14] 林晓东，朱林户，王瑛. 一种改进的基于概率假设密度滤波的多目标跟踪方法 [J]. 控制与决策，2011，26(9)：1367-1372.

LIN Xiaodong，ZHU Linhu，WANG Ying. Improved probability hypothesis density（PHD） filter for multi-target tracking [J]. Control and Decision，2011，26(9)：1367-1372.

[15] ZHANG Huanqing，YONG Jinlong，GE Hongwei，. An improved GM-PHD tracker with tracker management for multiple target tracking [C]// 2015 International Conference on Control, Automation and Information Science(ICCAIS)，Changshu，China，Oct 29-31，2015：185-190.

Labeling GM-PHD Filter with Spawning Targets

CHEN Jinguang1，ZHAO Tiantian1，MA Lili1，XU Bugao1,2

( 1. School of Computer Science, Xi’an Polytechnic University, Xi’an710048, China;2. School of Human Ecology, University of Texas at Austin, Austin 78712, Texas, USA )

The Labeling Gaussian Mixture Hypothesis Probability Density filter (LGM-PHD) cannot get the spawn targets. Addressing this problem, an improved algorithm is presented. Firstly, the labels are applied to the Gaussian items in the GM-PHD filter to distinguish different targets, and their tracks are determined. After that, in the period of filtering, the track labels between the current step and former step are matched, associated and maintained. Finally, the spawn threshold is used to determine if there are spawn targets or not and determine the number of possible spawn targets, then the labels for Gaussian items of new targets and possible spawn targets are reallocated. The simulation results show, in the situation of existing spawn targets, the improved algorithm has better tracking performance than the LGM-PHD.

probability hypothesis density filter; random finite sets; sate estimation; spawn targets; labeling GM-PHD

1003-501X(2016)12-0079-06

TP931

A

10.3969/j.issn.1003-501X.2016.12.013

2015-12-24；

2016-07-25

国家自然科学基金项目(61201118)；陕西省自然科学基础研究计划项目(2016JM6030)；西安工程大学研究生创新基金项目(CX201631)；西安工程大学学科建设项目

陈金广(1977-)，男(汉族)，河南南阳人。副教授，博士，主要研究工作是多源信息融合、目标跟踪。E-mail: xacjg@163.com。