电动机离散变频软起动分频及最优切换相位控制

周封， 曹俊雷， 刘健， 王丙全， 王晨光

（哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨150080）

电动机离散变频软起动分频及最优切换相位控制

周封， 曹俊雷， 刘健， 王丙全， 王晨光

（哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨150080）

为了提高重载时异步电动机离散变频软起动的性能，解决采用标准触发角起动中各频段切换时产生较大的转矩脉动及转速波动等问题，进行了分频相位组合以及最优切换相位的研究。通过对离散变频相位组合及其序分量的理论分析，得到合理的分频系数。针对三相不对称频段，采用对称分量法建立了相序分量表，求出了正序分量最大的相序组合。建立了离散变频软起动仿真模型，计算分析了各频段的电流和转矩，确定了最佳分频等级及过渡频段。对各频段采用不同切换相位进行仿真，得到了最优切换相位的确定规律。最终确定了一种最合理的离散分频软起控制方案，为离散变频闭环控制策略的研究提供了理论依据，为异步电机重载软起动提供了新思路。

异步电机；离散变频；最优分频等级；最优切换相位；软起动

0　引言

三相异步电动机作已被广泛应用于工矿企业、交通运输、国防工业等各个领域。据统计，异步电动机每年耗电量占全国发电量的50%以上。然而，电动机直接起动时出现的冲击电流一般高出额定电流7～10倍。这样大的电流不仅会使供电电网受到冲击，还会导致母线电压下降，从而影响电网供电质量，而且产生的巨大转矩冲击会使电动机发生猛烈振动［1-3］。

针对直接起动电流过大的问题，基于各种起动方法和控制策略的软起动技术相继出现，并形成了许多成熟的产品［4-5］。常规软起动器通过改变晶闸管的触发角调节电机的起动电压来减小起动电流，但由于电机的起动转矩与电压的平方成正比，因此当降压起动电动机时，会大大降低电动机的起动转矩［6］。

Ginart等人［7］提出离散变频软起动方法，该方法通过有选择地触发半波导通，达到了变压变频的目的，弥补了常规软起动器的转矩低的不足［8-10］。离散变频软起动方法提出后引起了学者的广泛关注，给出了合理的离散变频方案［11-12］，对离散变频理论进行了补充和发展。其他学者的研究主要集中在离散变频技术在提高电机转矩、降低起动电流的能力方面［13-16］。

目前研究仅限于离散变频过程的实现，而对于控制策略及性能优化等问题，如各频段之间如何优化切换相位、采用标准触发角控制时对电机起动特性的影响等均无相关研究。通过对当前采用的标准触发角离散变频控制进行分析发现，虽然能够实现电机高转矩、低电流起动，但当各频段间采用不同的切换相位时，会对电机的转矩脉动、以及转速连续性产生重大影响。

为了解决这一问题，本文提出了一种可应用于标准触发角离散变频控制中的最优触发脉冲产生策略，该策略可具体设置不同频段之间的切换相位，从而能够对离散变频过程中各频段之间不同切换相位对电机起动过程中转矩、转速波动的影响进行充分研究，以获得各频段最优切换相位，为离散变频软起动器具体软件系统的编制提供了参考依据，同时为离散变频控制策略的深入研究提供了理论基础，由于控制简便性及良好的起动特性，因此可在电机起动领域获得较广泛的应用，具有较高的工程应用价值。

1　离散变频相位组合及其序分量分析

1.1有效相位组合频段分析与确定

由于离散变频中各频段存在多种相位组合，且有些相位组合所对应的频段对起动电机是无效的，因此需要经过理论分析确定存在有效相位组合的频段。

一般用下式表示三相电压瞬时值：

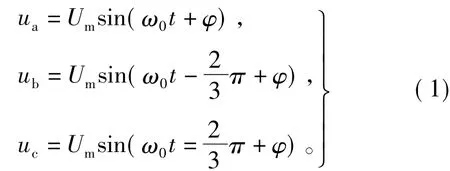
式中ω0=2πf0，其中f0=50 Hz；，其中Up为相电压有效值；φ为电压初始相位。

设离散变频后新的分频电压的角频率为ωn，分频数为n，则有

由上面分析可得出分频后三相电压的基波分量应满足下面的公式：

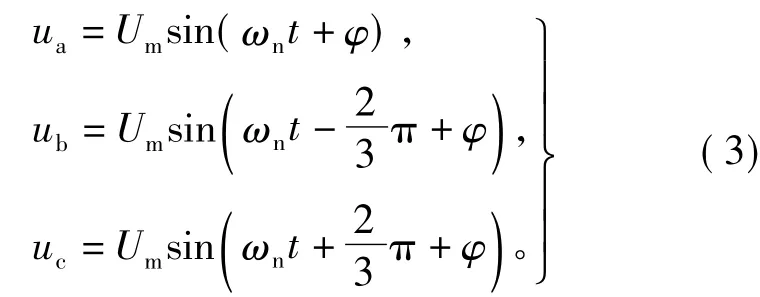
为简化分析，将分频后A相基波电压的过零点与电网A相电压的过零点一致，即：令φ=0，则此时B相基波电压的过零点的应满足：

将式（2）代入式（4），可得

为降低成本，离散分频技术使用的开关管为晶闸管，其关断不可控，依靠电压过零后晶闸管自然关断，因此，离散分频控制必须保证变换后的电压输出周期为工频周期的整数倍，才能保证变频后的电压平稳，由此规律可确定分频后的相电压过零时刻一定是工频电压过零。工频B相电压过零点应满足下式：

为了保证分频后A、B、C三相电压基波分量依然为对称关系，因此需要使分频后B相的过零点为电网B相过零点的其中一个，且分频后B相过零点应满足下式：

由式（7）可知，若要使分频系数n为整数，m应为偶数。因此当m=2、4、6…时，通过上述两式即可求得相应的分频系数，同时也可知道该分频系数下电压基波分量的相序。例如：当m=2、4、6…时，代入式（7）可得n=4、7、10…，此时分频后的电压基波分量为正序，即三相完全对称。而n不满足上述条件时，存在负序分量，此时三相不对称，需要进行进一步分析。

假设分频后三相电压与电网电压相序相同，但三相不对称，设分频后基波分量中B相滞后A相的角度为θB，可将式（4）变为

上式两边同时乘上分频数n可得到

从而求出分频后B相信号的初始相位θB

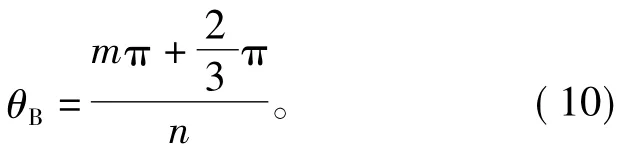
同理可得C相信号的初始相位θC

由于电网电压波形在一个周期中存在正、负两个过零点，因此在分频电压中所包含过零点数量为

以A相为参考相，B相电压基波分量的初始相位可选择值存在k种。且k决定了式（10）、式（11）中过零点序号m的取值范围，即m=0、1、2、…、k-1。同理，A、B、C三相电压可能的组合数共有k2种。根据式（10）、式（11）分别计算出各级子频率系统的相位角列表1、表2所示。

表1　n=2时分频后B、C相基波分量的初始相位（θA=0°）Table 1　Initial phase of the fundamental component about B，C phases after frequency splitting when n=2

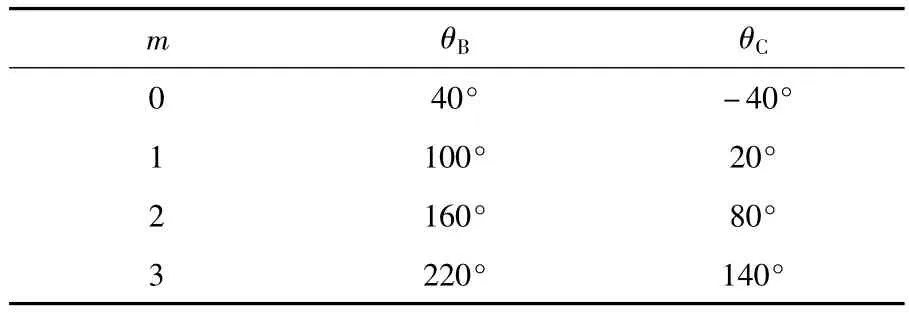
表2　n=3时分频后B、C相基波分量的初始相位（θA=0°）Table 2　Initial phase of the fundamental component about B，C phases after frequency splitting when n=3

1.2三相不对称时正序分量最大的相位组合研究

与确定

由以上分析可知，在各频段能够产生正序分量的相位组合存在多组，因此需要对各频段下的具体相位组合进行分析，以确定能够产生最大正序分量的相位组合，从而确定具体的晶闸管触发方式。

为此在确定了2、3分频可出现的相序组合后，由对称分量法可求出不同相序组合下的正序、负序和零序分量的含量，其中只有正序分量才可使电机正转，因此需要采用对称分量法求出正序分量最大的相序组合。

对称分量法可表示为

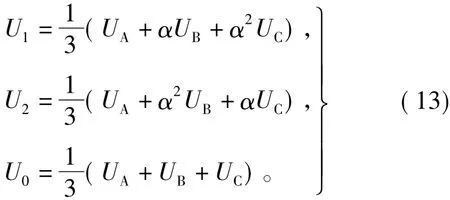
式中，U1、U2分别为正负序分量，α=ej120°。

将2分频的各种电压相序组合用对称分量法分析后，其各序分量值如表3所示。

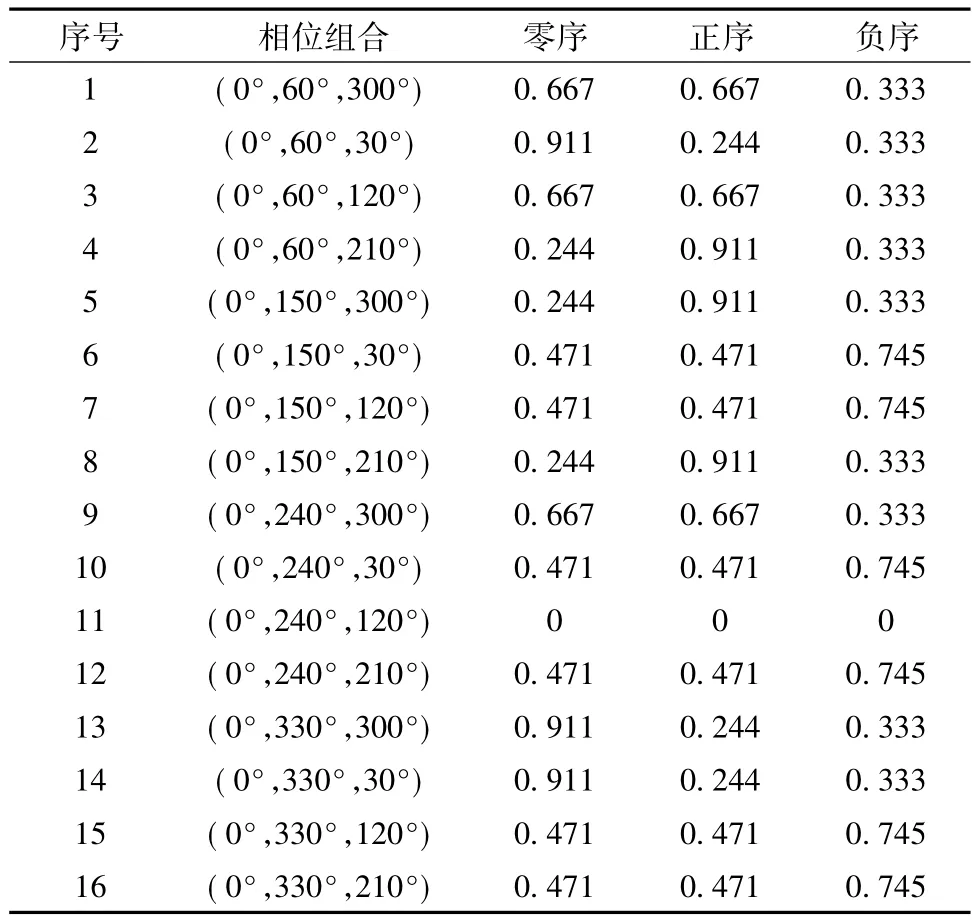
表3　2分频相序分量表Table 3　Phase sequence subscale of 2 splitting frequency

由表中可知，相位组合（0°，60°，210°）、（0°，150°，210°）、（0°，150°，300°）时，2分频的正序含量最大。同理，可求出相位组合（0°，100°，260°）、（0°，100°，200°）、（0°，160°，260°）时，3分频正序含量最大。

2　离散变频软起动系统结构及仿真建模

离散变频软起动控制系统结构如图1所示。其基本原理是用控制器控制双向晶闸管连续半波导通与关断，实现三相电源等效分频，进而实现异步电动机离散分频软起动控制。

图1　系统结构框图Fig.1　Diagram of the system structure

离散变频软起动器的仿真模型由三相电源、触发角模块、脉冲发生器模块、三相接触器、晶闸管组、电动机测量模块组成，其具体结构如图2所示。其参数如下：PN=7 500 W，VN=400 V，fN=50 Hz Lm= 0.124 2 H，RS=0.738 4 Ω，L1S=0.003 045 H，Rr= 0.740 2 Ω，L1r=0.003 045 H，p=2，J=2.67kg·m2。

图2　标准触发角离散变频软起动仿真模型Fig.2　Simulation model of discrete frequency conversion soft starter under standard trigging angle

3　最佳分频等级及过渡频段分析确定

3.1最佳分频等级分析及确定

实践证明，电动机供电频率越低，起动转矩越大，同时电动机的起动电流也相对比较小。电动机工频条件下的起动力矩相对较小，重载条件有时甚至无法完成起动，此时可选择使用离散变频技术，提高电动机的启动转矩，顺利起动电机。然而，离散分频的频率怎么选择，其相邻两个分频频率之间过渡方案怎样设计，这些都是影响其效果的主要因素。

在选择使用三相对称的分频频率，其主要出发点是提高电动机的正向力矩，减少电动机的振动，降低电动机的发热，故优先选择4分频、7分频、10分频和13分频。

图3为13分频、10分频、7分频的电机起动电流、转矩有效值波形图，图3（c）、3（d）分别为10分频下电机起动电流、转矩有效值波形图，图3（e）、3（f）分别为7分频下电机起动电流、转矩有效值波形图。

由图3可知，当采用半波方式触发时，不同频段下的电流随分频数的减小而减小，转矩在13分频与10分频时相差不大，但采用7分频时，转矩随着时间的延长而增大，电机在13分频及10分频起动时，转矩升高到额定运行时的5倍，电机在7分频运行时，初始转矩为额定值的3倍，但其转矩随时间增加而逐渐升高，因此采用该频段起动电机波动较小。由电流波形图可知，电机电流在上述三个频段下几乎均为额定值的4倍左右，为了尽可能缩短电机的起动时间并减小两频段之间的速度差以减小电机的震荡，不选用10分频，初步选定的频段应包含13分频和7分频。在正序对称的频段中，4分频最接近工频，因此频率选择必须包含4分频。

3.2最优过渡频段的分析与确定

使用离散分频技术起动电动机时，若只考虑选择三相对称的频段，则直接从4频段切换至工频，其转速会骤升，不利于电机稳定运行。图4为从4频段切换至工频时的电动机运行仿真曲线，由图中可看出，由于起始转速的限制会导致电机的反电势较小，因此使电机电流迅速升至额定值7倍左右，且电机在切换瞬间会剧烈振动。

为了避免上述情况的发生，下面就离散变频过程中高频段可能的切换方式进行分析和研究，为了寻找切换过程中波动最小的过渡频段，首先对3分频及2分频下电机转矩的大小进行分析。由上文可知，2分频中相序组合大部分负序分量含量较大，（0°，60°，210°）、（0°，150°，210°）、（0°，150°，300°）为2分频中正序分量最大的相序组合，同时确定了（0°，60°，210°）为其最佳相序组合，上文也已求出了3分频的最佳相序组合。

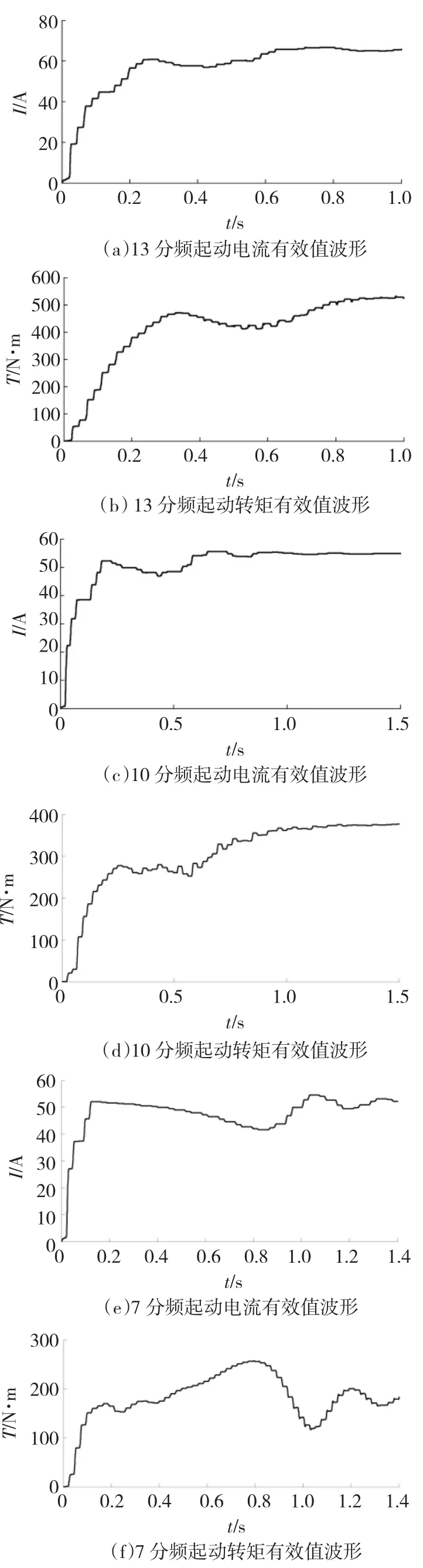
图3　各频段起动情况Fig.3　Starting condition under different frequency splitting

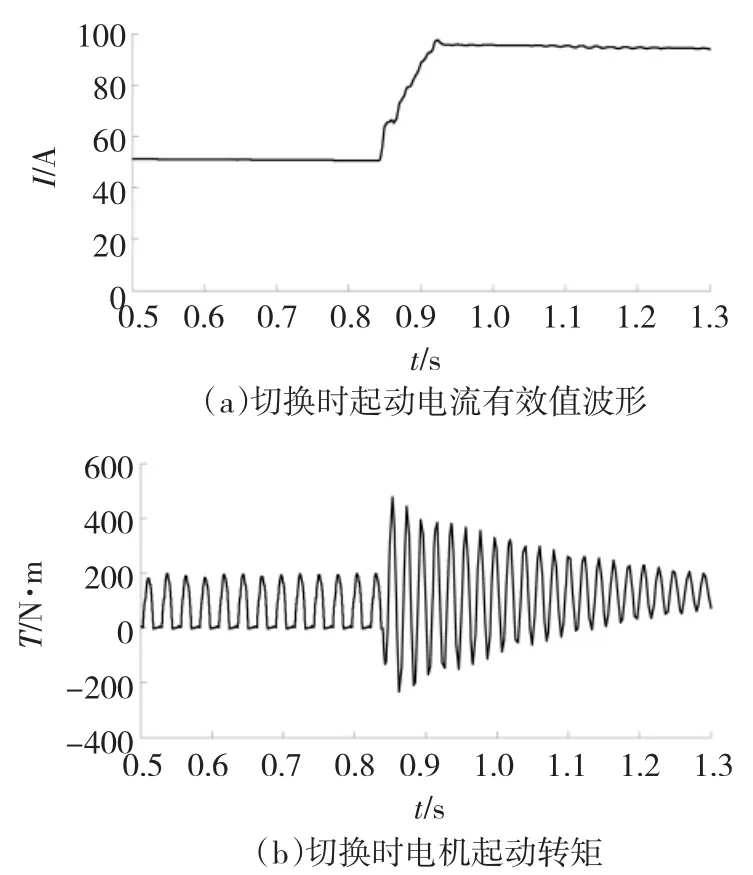
图4　4分频过渡到工频情况Fig.4　Situation of the transition from four splitting frequency to power frequency

图5为电机在f/4-f/3-f/2-f下电机转矩波形图，从图可以看出，电机在4分频到3分频的切换瞬间转矩未发生较大波动，但当3分频切换到2分频时，由于2分频中含有大量的负序分量，因此该频段下电机的转矩较小，使电机的起动时间加长，电机大约运行了3s左右，才达到2分频额定转速，而3分频在整个离散变频起动过程中只运行了0.9s左右，其转速即可达到3分频的额定转速，且整个过程中转矩未出现波动。考虑到2分频的负序分量相对较大，启动速度相对缓慢，对电动机非常不利，故选择三分频作为最后切入工频的频率，即离散变频切换形式为f/13-f/7-f/4-f/3-f。

图5　f/4-f/3-f/2-f下电机转矩波形图Fig.5　RMS current and torque waveforms of the motor under f/4-f/3-f/2-f

4　各频段最优切换相位分析与确定

在整个起动过程中，共有四次频率切换：开始频率f=3.85Hz；而后依次切换到 f=7.14Hz、f= 12.5Hz、f=16.7Hz、f=50Hz。不同频率间切换时，由于不同频率供电的波长不同，三相电压不能同时保证切换前后相位一致，必然导致电动机内部磁场需要重新构建，这将导致在切换的瞬间电动机会出现转速和出力下降、振动增大等现象，需要对不同切换角度下的过渡过程进行研究，找到一种转速和转矩平滑过渡的切换方案。

4.113分频最优切换相位分析及确定

图6、图7分别为13分频不同切换相位下转速波形和转矩波形，可以看出，转速和转矩波动之间是紧密对应的。当13分频采用1/4周期切换时，转速下降幅度最大；当采用1/2、3/4周期切换时，转速下降幅度比上述情况要小；因此当选择最优切换相位时，应排除掉13分频1/4周期切换。当采用1/2周期切换时，在13分频与7分频切换时刻转矩波动最大；当采用3/4周期切换时，只是在某一段切换时出现了转矩的较大波动，而1/2周期切换却出现了两次大的转矩波动，因此，当采用13分频3/4周期切换时，对电机的转矩和转速的影响最小，即该切换相位为13频段与7分频切换时的最优切换相位。

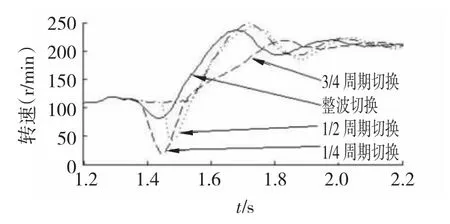
图6　13分频整、1/4、1/2、3/4周期切换时转速波形图Fig.6　Speed waveform switching at the whole，1/4，1/2，3/4 cycle of thirteen splitting frequency

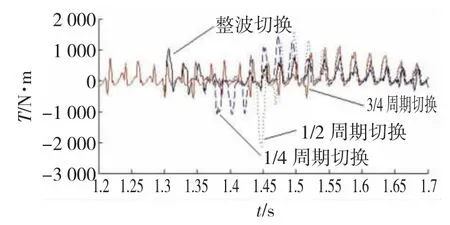
图7　13分频整、1/4、1/2、3/4周期切换时刻转矩波形放大图Fig.7　Torque partial enlarged view of the motor at each band switching at the whole，1/4，1/2，3/4 cycle of 13 splitting frequency

4.27分频最优切换相位分析及确定

图8为7分频不同切换相位下转速波形比较图。采用整周期切换时，7分频与4分频切换转速下降幅度较大；当采用3/8周期切换时，转速波动最小，转速降也最小。因此，7分频3/8周期切换为离散变频过程中的最优切换相位。

图8　7分频整、1/4、3/8、5/8周期切换时转速波形图Fig.8　Speed waveform switching at the whole，1/4，3/8，5/8 cycle of 7 splitting frequency

4.34分频最优切换相位分析及确定

图9为4分频不同切换相位下转速波形图。当4分频采用整周期切换时，转速下降幅度较另外三种情况要小得多。故4分频选择整波切换控制策略。

图9　4分频整、1/4、1/2周期切换时转速波形图Fig.9　Speed waveform switching at the whole，1/4，1/2 cycle of 4 splitting frequency

至此，得到了异步电动机离散分频软起动切换角控制方案，即在整个离散变频启动过程中，13分频采用3/4周期、7分频采用3/8周期、4分频采用整周期切换，可实现转速及转矩波动最小的起动过程。

4.4各分频采用最优切换相位启动过程

通过上述分析，可计算得到图10的最优切换相位启动速度仿真曲线，图11为对应的电流变化曲线。可以看出，电动机在频率切换过程中会出现短时的转速波动，这种频率切换带来的影响是不可避免的，但通过控制，可减轻影响。在离散分频启动过程中，电动机的电流峰值接近于直接启动电流峰值，但由于分频后电流不是连续的，电动机电磁功率下降很多，可降低对电源功率的要求。

在各频段最优切换相位的基础上，可具体计算出每一频段工作时间，而后可在开环离散变频控制程序编写过程中，对各频段运行时间及切换时间进行具体设置，即可实现最优切换相位的效果。

图10　全部启动过程转速曲线Fig.10　Curve of rotational speed during starting process

图11　启动过程电流曲线Fig.11　Curve of current during starting process

5　结论

本文提出了一种新型的最优触发脉冲发生控制策略，在分析确定最佳分频等级及过渡频段的基础上，对各频段最优切换相位进行了逐级优化分析。结果表明：

1）确定了离散变频过程中的最佳分频等级即f/13-f/7以及最优过渡频段即f/4-f/3-f，电机在选定的最优过渡频段下，电机输出转矩较大，且各频段转矩波动较小，可大大缩短电机的起动时间。

2）采用所求得的最优切换相位即13分频3/4周期切换、7分频3/8周期切换及4分频整周期切换，可采用标准触发角控制与最优切换相位相结合成为新的控制策略，该策略可较大程度简化离散变频软起动程序，且能够大幅度减小该控制下电机在不同频段切换瞬间转矩和转速的波动。

该控制策略对离散变频采用频段时间控制具有较高的参考价值，同时为离散变频其他控制策略提供了理论基础，具有较高的理论价值；由于其可大幅度减小电机振动，能够防止电机在起动过程中发生机械损伤，可广泛应用于电机软起动领域，因此该控制策略具有较高的工程实际应用价值。

［1］甘世红，褚建新，顾伟.基于开关变压器的中压异步电动机软起动器［J］.中国电机工程学报，2005，25（16）：153-157. GAN Shihong，CHU Jianxin，GU Wei.Middle-Voltage AC motor soft starter based on the ON-OFF transformer［J］.Proceedings of the CSEE，2005，25（16）：153-157.

［2］吕广强，纪延超，俞红祥.基于自关断器件的新型软起动［J］.中国电机工程学报，2004，24（5）：141-147. LÜ Guangqiang，JI Yanchao，，YU Hongxiang.A novel soft starter for induction motors based on self-commutated switches［J］.Proceedings of the CSEE，2004，24（5）：141-147.

［3］Gürkan Zenginobuz，Isik Cadirci，Muammer Ermis，etc.Performance optimization of induction motors during Voltage-Controlled soft starting［J］.IEEE Transactions on Energy Conversion，2004，6 （19）：278-288.

［4］Chia-Chou Ye，Demerdash N.A.O.Fault-Tolerant Soft Starter Control of Induction Motors With Reduced Transient Torque Pulsations［C］//IEEE Power Electronics Specialists Conference，2009：848-859.

［5］RAJAJI L，KUMAR C.Adaptive Neuro Fuzzy based Soft Starting of Voltage-Controlled Induction Motor Drive［C］//IEEE South East Con April 3-6，2008，Tamilnadu，India.2008：448-453.

［6］佘致廷，皮玉，周米洋.感应电机离散变频高转矩软启动器的研究［J］.电气传动，2010，40（3）：17-19. SHE Zhiting，PI Yu，ZHOU Miyang，et al.Research on high torque starter of induction motors based on discrete variable frequency ［J］.Electric Drive，2010，40（3）：17-19.

［7］佘致廷，郑勇，张前海.基于多级离散变频的高转矩软启动技术［J］.电源技术，2012，36（9）：1374-1376. SHE Zhiting，ZHENG Yong，ZHANG Qianhai，et al.High torque soft start technology based on Multilevel discrete variable frequency ［J］.Chinese Journal of Power Sources，2012，36（9）：1374 -1376.

［8］赵凯岐，王毅，徐殿国，等.晶闸管控制的感应电机中提高起动电磁转矩的一种新策略［J］.中国电机工程学报，2004，24 （3）：145-150. ZHAO Kaiqi，WANG Yi，XU Dianguo et al.A new strategy to improve electromagnetic starting torque for thyristor controlled induction motors［J］.Proceedings of the CSEE，2004，24（3）：145 -150.

［9］DU Jiang，MO Guofan，WU Guowei.An Improved Method for Induction Motor Constant Current Soft-starting Using Fuzzy-control ［C］//Sixth International Conference on Fuzzy Systems and Knowledge Discovery，2009：52-56.

［10］Nied A.，de Oliveira J.，de Campos R.F..Soft Starting of Induction Motor with Torque Control［C］.IEEE Industry Applications Society Annual Meeting，2008：1-6.

［11］王毅，赵凯岐，徐殿国.电机软起动控制系统中功率因数角的研究［J］.中国电机工程学报，2002，22（8）：82-87. WANG Yi，ZHAO Kaiqi，XU Dianguo.Research on displacement angle in the control system of motor soft starter［J］.Proceedings of the CSEE，2002，22（8）：82-87.

［12］李冬辉，吴昊，段克亮.基于离散变频技术的电机重载软起动系统［J］.天津大学学报，2009，42（6）：471-475. LI Donghui，WU Hao，DUAN Keliang.Heavy-Load soft starting of induction motor based on discrete variable frequency technology ［J］.2009，42（6）：471-475.

［13］严垚，王宏华.异步电动机离散变频软启动技术的发展［J］.机械制造与自动化，2012，6：196-199. YAN Yao，WANG Honghua.Development of discrete variable frequency induction motors soft starter［J］.Machine Building&Automation，2012，6：196-199.

［14］佘致廷，肖岸文，董璞.基于分级变频高转矩软起动器的研究［J］.湖南大学学报，2004，31（6）：46-50. SHE Zhiting，XIAO Anwen，DONG Pu.Study of high torque soft starter based on discrete frequency［J］.Journal of Hunan University，2004，31（6）：46-50.

［15］ 钟士元，田建设.基于MATLAB的模糊异步电动机软起动系统的仿真［J］.计算机仿真，2005，22（7）：157-160. ZHONG Shiyuan，TIAN Jianshe.MATLAB-based simulation of fuzzy system for soft-starting asynchronous motors［J］.Computer Simulation，2005，22（7）：157-160.

（编辑：刘素菊）

Optimal switching phase and frequency splitting strategy of discrete frequency conversion soft starting control for asynchronous motor

ZHOU Feng， CAO Jun-lei， LIU Jian， WANG Bing-quan， WANG Chen-guang
（College of Electrical and Electronic Engineering，Harbin University of Science and Technology，Harbin 150080，China）

In order to improve the performance of discrete frequency conversion soft starting of asynchronous motors with heavy loads and the problems were solved，such as the pulse of torque and fluctuation of speed when switched in every frequency band by using standard triggering angle during starting process，the frequency splitting phase and the optimal switching phase was discussed.The reasonable frequency splitting factor was obtained by analyzing the combination relationship of frequency splitting phase as well as its sequence components.For the unbalanced three-phase frequency bands，the form of the phase sequence components was established and the phase sequence combination with the largest positive sequence component obtained by using the symmetrical component method.The simulation model of discrete frequency conversion soft starting was established，the current and torque in every frequency band was calculated and analyzed，thereby the best discrete frequency conversion level and transition frequency band was determined.Each frequency bands with different switching phases was simulated and the law of optimal switching phase was obtained.Finally，the most reasonable control scheme of discrete frequency conversion soft starting was determined，which provided the theoretical basis for the research of discrete frequency conversion closed-loop control strategy and a new idea for the soft starting of asynchronous motors with heavy loads.

asynchronous motors；discrete frequency conversion；optimal discrete frequency conversion level；optimal switching phase；soft staring

10.15938/j.emc.2016.03.003

TM 346

A

1007-449X（2016）03-0013-07

2014-03-27

黑龙江省科技计划（攻关）项目（GZ11A213）

周封（1970—），男，博士，教授，研究方向为大型电机综合物理场计算工业设备节能控制与故障监测，新能源发电监测控制等。

周封