考虑天气因素的输电网可靠性区间评估及其仿射算法

李小燕，丁 明，齐先军



考虑天气因素的输电网可靠性区间评估及其仿射算法

李小燕，丁 明，齐先军

(安徽省新能源利用与节能省级实验室(合肥工业大学), 安徽 合肥 230009)

为了考虑故障率和天气因素的不确定性对电网可靠性评估的影响，在输电线路分段模型的基础上，引入区间概率用于可靠性参数不确定的元件停运率建模。采用状态枚举法和区间运算对IEEE-RBTS系统进行可靠性评估。针对区间运算结果过于保守的问题，引入仿射算法，有效缩减了计算结果的区间范围。计算结果表明，天气因素对输电网可靠性评估的影响不容忽视，区间数形式的可靠性指标可以反映不确定部分的大小，证明了该方法的合理性和有效性。

天气因素；输电网；可靠性评估；区间概率；仿射算法

0 引言

由于运行环境的差别，电力系统中输电设备的故障率一般高于发电设备，重要输变电设备的停运是引起系统潮流转移，诱发大面积停电事故的关键，往往会造成严重的社会和政治经济影响[1-2]。在恶劣天气条件下，元件发生故障的机率明显增加，并使输电网发生多重相关或不相关故障的可能性急剧增大，即出现所谓的“故障聚集”现象[3]，因此在电力系统可靠性评估中考虑恶劣天气的影响是十分必要的。对于横跨多种复杂气候条件的长距离输电线路而言，恶劣天气的影响往往是局部而非全局性的，因此一条线路的不同地段可能处在不同天气环境下，采用均匀的气候状态建模不能得到合理的结果，有必要建立更为细致的分段可靠性模型。

目前的文献一般将影响电力系统运行的天气分为正常天气、恶劣天气和大灾难天气，采用两状态或三状态模型来描述不同天气情况下的故障率[4-6]，采用蒙特卡罗抽样或状态枚举法进行计算[7]，这些方法都是基于输电元件的精确停运模型，采用传统的精确概率评估天气对输电网络可靠性的影响。统计数据的缺失和天气情况的复杂性导致了可靠性评估原始数据(输电元件的故障率、修复率等)存在很大的不确定性[8-9]。对于不确定性问题的处理一般采用模糊集理论、灰色系统理论和区间分析方法[10-11]。采用模糊集理论时，隶属函数的确定和指定参数的模糊化会掺杂人为因素并失去有用信息；灰色系统理论对参数要求不高，但分辨系数的确定带有一定的主观性；而运用区间分析求解不确定性问题可以减少人为因素的影响，提高分析结果的可信性。文献[12]将区间数学思想引入可靠性评估，以对大量不确定信息加以科学的处理。文献[13-15]考虑原始参数的不确定性，采用区间算法对配电系统进行可靠系统性评估。输电系统由于跨度大、不同区域甚至同一条线路可能出现多种复杂气候需要分别、分段模拟，与配电系统可靠性建模有明显差别，运用区间分析方法研究受天气因素影响的输电网可靠性评估是必要的。

本文将线路可靠性模型与区间概率理论结合起来[3,16]，建立了输电系统非精确可靠性评估模型，采用区间指标评价输电系统可靠性；为了克服传统区间运算由于忽略变量之间相关性造成运算结果过于保守的问题[17]，本文在区间运算中进一步引入仿射算法，缩减了区间宽度，获得更为精确的区间可靠性指标。

1 区间运算和仿射算法

1.1 区间运算

文献[18]详细阐述了区间概率的定义及性质。由于区间概率是区间数，所以其运算符合区间运算法则。设，为区间数，区间运算规则如下。

区间运算的缺点是过于保守，得到的区间往往比实际范围大的多。例如对于区间数，，不等于0。这是由于在区间运算中认为两个区间数是相互独立的，而忽略了其相关性造成的。在科学计算中，如果不考虑这种相关性，尤其在一个接一个区间运算的长计算中，将会导致区间结果远远超过真实值的范围，这称为区间运算的“不独立性”。

1.2 仿射算法

为了解决区间运算“不独立性”问题，引入仿射算法予以改进[19]。假设变量，其仿射型为，其中是大小未知的实变量，称为噪声元，并且各个噪声元是相互独立的。是的中心值，R是对应于的偏增量。每个噪声元代表了量的所有不确定性中的一个独立的元素，相应的系数给出了这个元素的大小。

区间数和仿射型是可以相互转化的，如式(1)所示。

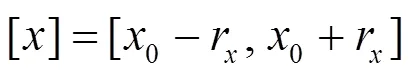
(2)

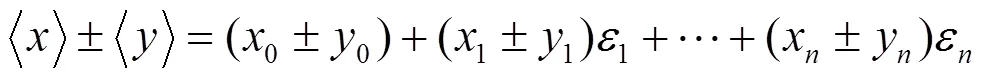
(4)

(5)

2 可靠性评估模型

2.1 元件概率的区间运算

(1) 元件概率区间值的一般计算

(8)

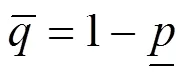
(2) 长距离输电线的区间概率

对于长距离输电线路，可能会经历不同的气候区域。为减少可靠性评估误差，对此类线路采用分段模拟，不同天气条件下的各线路分段采用不同的故障率、修复率表示，整条线路可以看成由不同故障概率元件串联起来的元件，如图1所示，其中是各分段的故障率区间值，是总分段数。

图1 输电线路分段模拟等效元件

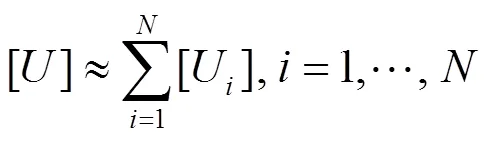
(11)

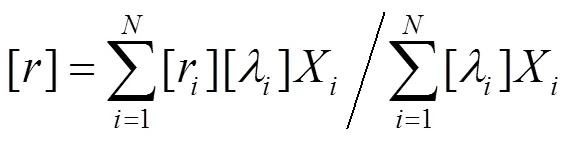
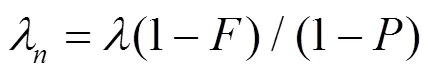
(14)

式中：为故障发生在恶劣天气下的比例；为恶劣天气出现的概率。考虑天气状态变化的不确定性按一定比例形成区间值，而一般采用点值。

2.2 系统状态选择和分析

在发输电组合系统中，输电部分故障概率比较小，采用蒙特卡洛抽样法形成多重故障的可能性很小，不利于可靠性指标的累计，不能准确评估天气对输电线路运行的影响，故在本文中采用状态枚举法。

在可靠性评估中，对每一个状态，如果出现元件停运情况，要进行系统状态分析，包括潮流分析和最优负荷削减。本文采用直流潮流确定节点过负荷和线路越限情况，运用发电有功再调度模型计算必要的负荷削减量及削负荷地点[20]，该计算采用实数运算而非区间运算。

2.3 可靠性指标的区间运算

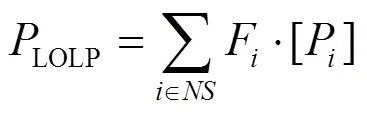
(17)

(18)

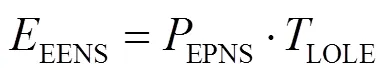
2.4 基于仿射算法的流程图

上述可靠性指标计算采用的是区间运算，结果的区间过宽，可信度降低。采用1.2节介绍的仿射算法代替区间运算可以得到更窄更精确的区间值，具体流程如图2所示。

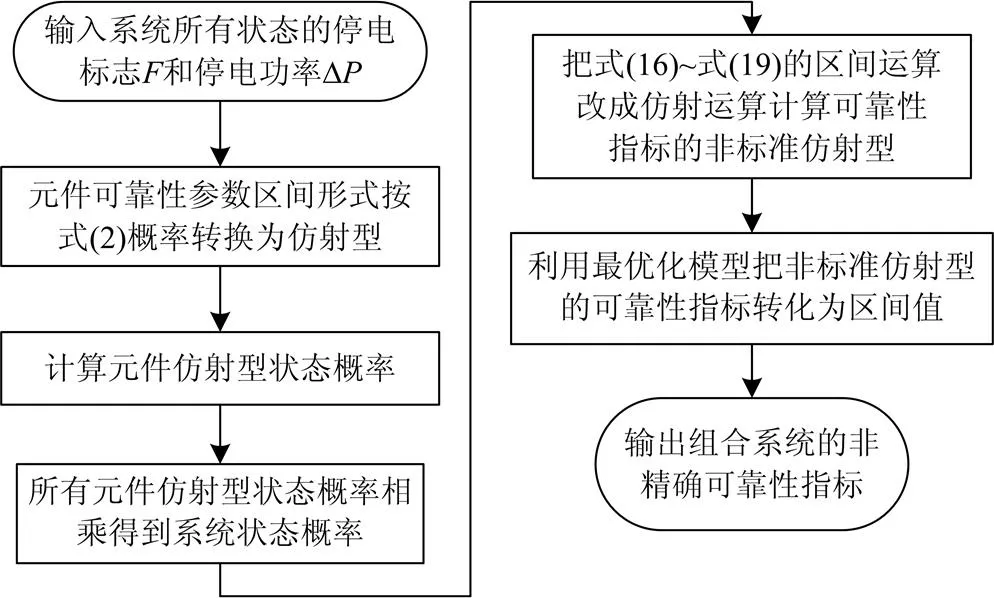
图2 基于仿射算法的区间值计算流程图

3 算例分析

本文以IEEE-RBTS[21]可靠性测试系统进行发输电系统可靠性评估计算。RBTS系统有6个节点，11台发电机组，9条输电线路，总装机容量为240 MW，总负荷为185 MW。因为大灾难天气出现的几率很小，所以只考虑两状态天气，即正常天气和恶劣天气。根据文献[8]的资料和的取值分别为0.4和0.018，恶劣天气下平均修复时间为正常的1.5倍，讨论以下算例。

算例 1：仿射算法对区间运算的改进

假设系统中线路5、8、9处于恶劣天气下，考虑天气变化的不确定性以变化形成区间故障率，其他元件参数为点值。分别利用区间运算和仿射算法得到系统的可靠性指标如表1，其中表示区间数上下界之差。从表1中可以看出区间结果都包含了点值，表明区间运算的合理性。比较两种算法的结果发现采用仿射算法得到的区间更窄，所以仿射算法的精度更高，更具实际参考价值。以下其他算例均采用仿射算法。

表1 区间运算及仿射算法结果

算例2：天气状态不确定性对可靠性影响

天气对系统影响的不确定性表现为受天气影响线路故障率的波动。图3给出了LOLP指标随故障率波动的变化曲线。从图3可以看出，随着故障率波动增加，可靠性指标的区间宽度都增加，表明元件参数的不确定性最终体现在可靠性指标上；区间值能反映可靠性原始参数在一定范围内变化所导致的可靠性指标的变化，即通过一次计算可以合理评估天气变化对系统可靠性的影响，避免多次点值评估造成计算量增加。

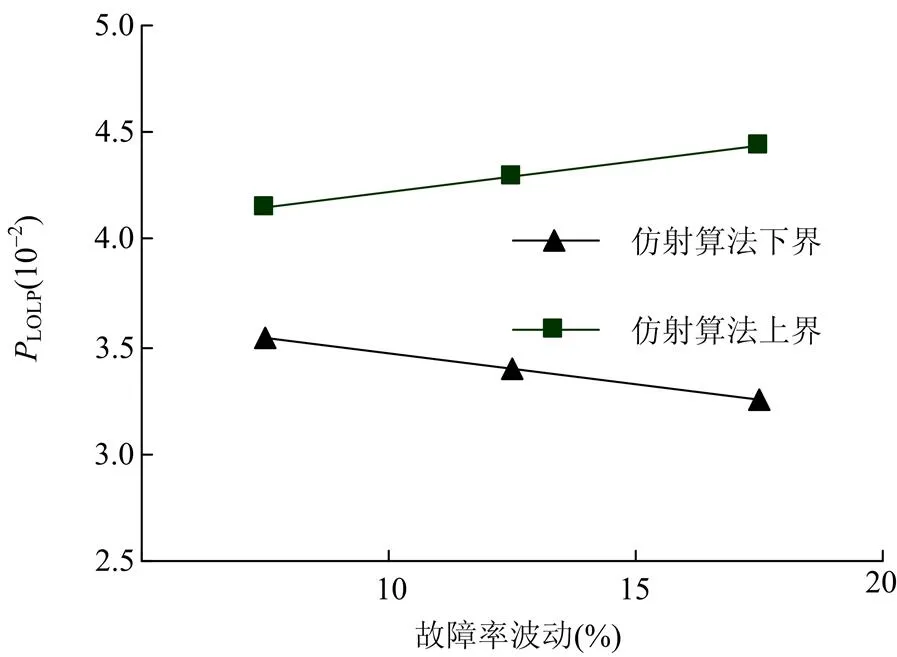
图3 可靠性指标随故障率变化曲线

算例3：值对可靠性的影响

值反映了线路“故障聚集”程度，值越大线路故障率越高，而且不同地理地区的值是不同的，例如在地形复杂的山区值较平原地区要高。不同的值，可靠性指标变化如图4所示，以LOLP和EENS指标为例。

从图4中可以看出随着的增大，指标呈快速增长趋势，并且其区间宽度也变大，所以当值较大的情况下，采用区间概率用于可靠性评估其精度会下降。

算例4：线路分段模拟的作用

对长距离输电线路，可能出现一条线路跨越多个天气区域的情况，在可靠性评估中如果认为这些线路处于同一个天气状态下，所得结果可能过于乐观或悲观。在RBTS系统中，线路2，3，7为长距离输电线路，假设以节点2为中心，三条线路各有50%区域处于恶劣天气，剩下50%处于正常天气，可靠性参数同算例 1，计算结果如表2所示。方案1：整条线路处于恶劣天气状态下；方案2：线路部分处于恶劣天气状态。

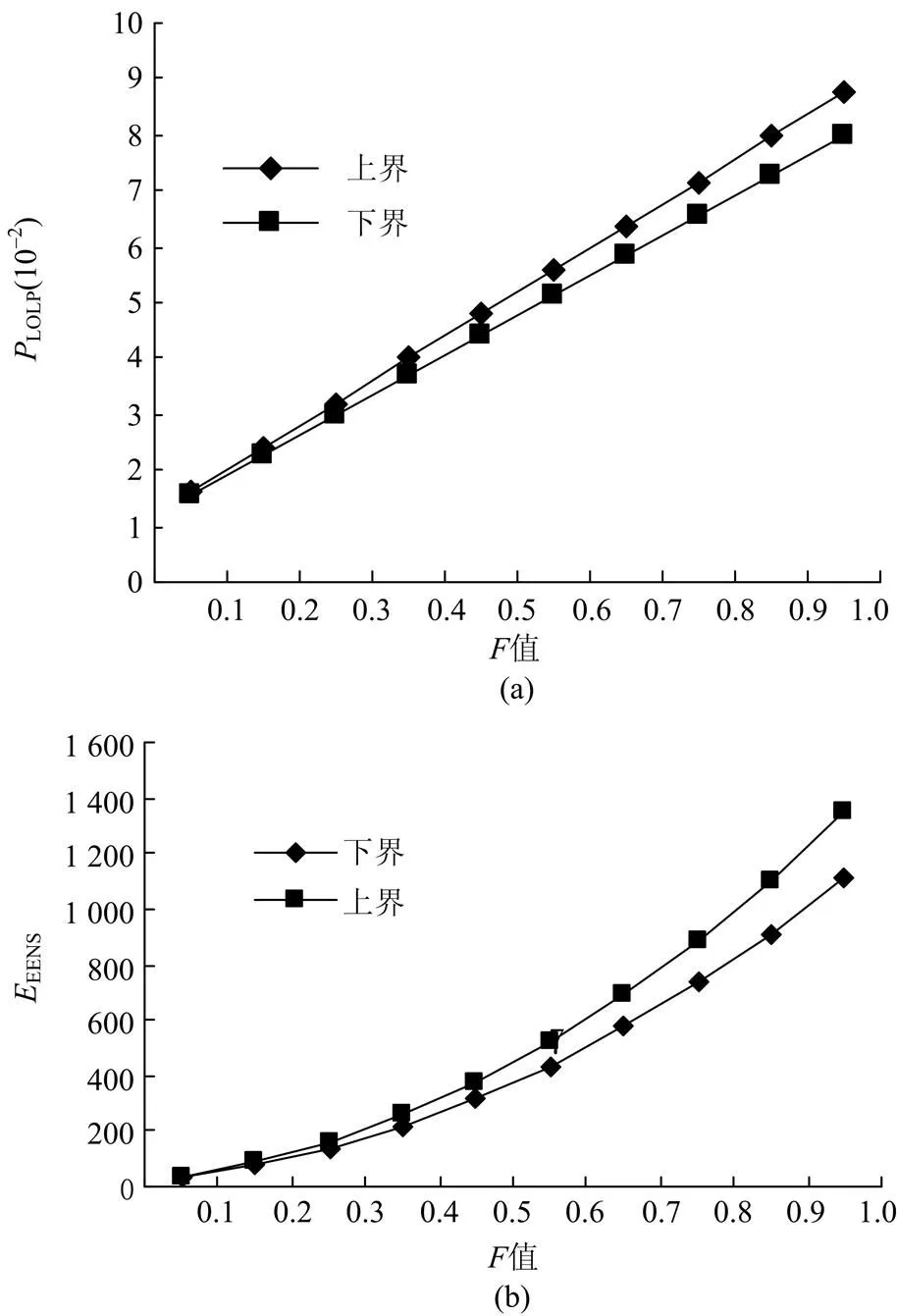
图4 F值对可靠性指标的影响

从表2中可以看出相比方案1，在方案2中各可靠性指标都有明显下降，即风险变小，这与实际情况吻合，所以在输电网络可靠性评估中考虑线路受天气因素影响时，不能忽视线路所处地理区域不同而导致的气象影响的不均匀性。

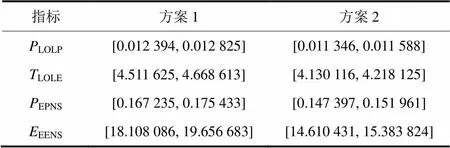
表2 不同天气状态下的可靠性指标

图5给出了各节点的可靠性指标相对误差绝对值区间数，相对误差计算以方案1为基准值。从图5中可以看出各节点受天气影响程度不一，2号节点受影响最小，因为2号节点装有发电机，其削负荷主要由发电容量不足引起，线路故障对其影响甚少。其他通过线路和发电机相连的各节点受天气影响较大，尤其是3、4号节点EENS指标相对误差较大，说明其对天气状态较敏感。

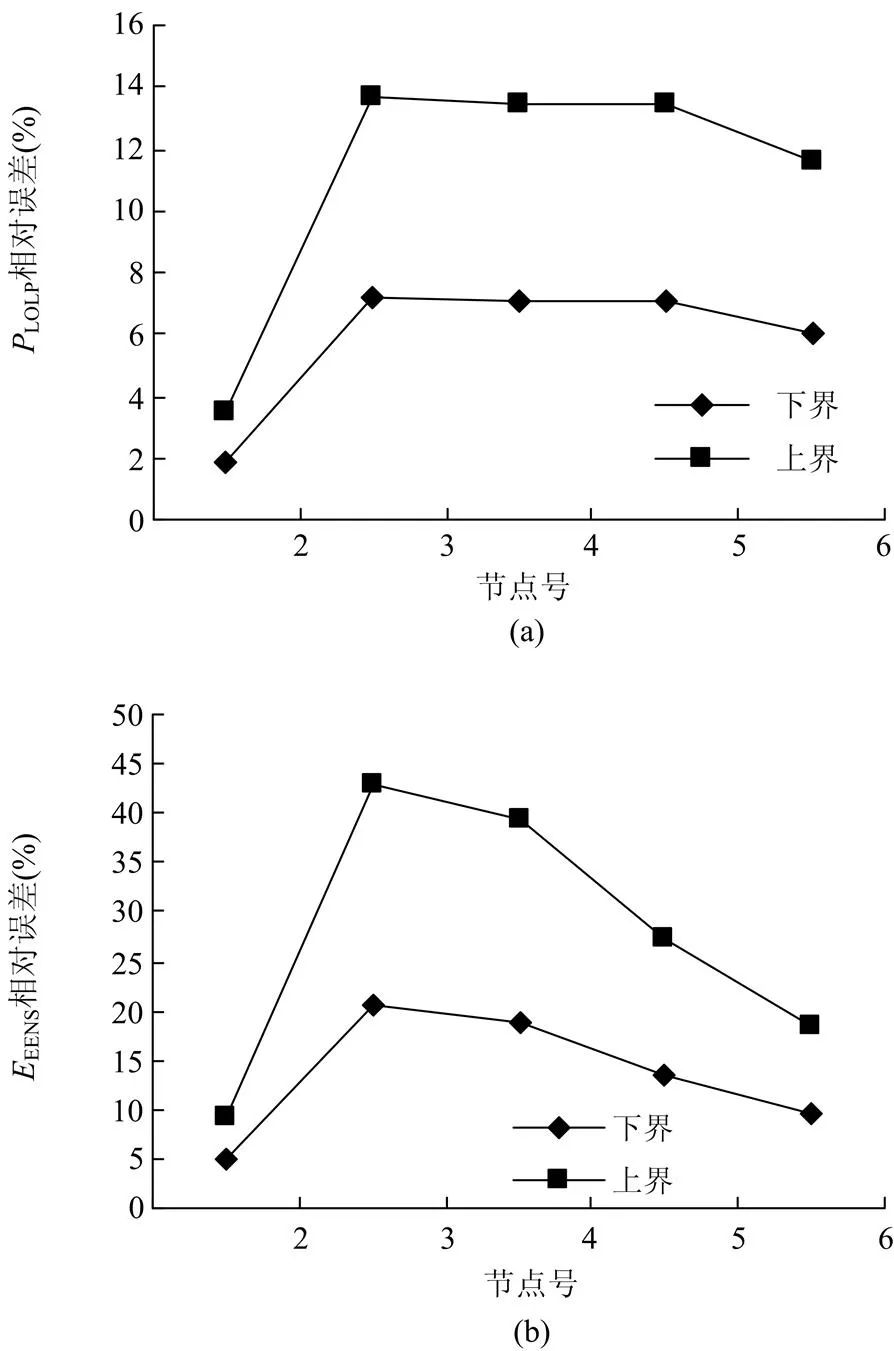
图5 节点可靠性指标相对误差

4 结语

本文分析了天气因素对输电网可靠性的影响，采用区间概率用于线路可靠性建模，区间概率相比点概率更能体现气象因素的不确定性。仿射算法解决了区间算法结果过宽的问题，得到的结果更为精确。

考虑长距离输电线由于所处地域不同导致天气因素影响不均匀性，采用分段模拟法用于该类元件的建模，结果表明该模型解决传统模型过高评估天气输电网可靠性的影响的问题。

故障发生在恶劣天气下的比例值的大小对可靠性指标的影响较大，随着增大，系统可靠性水平急剧下降，所以对电力部门来说不可忽视恶劣天气对电网运行的影响。

恶劣天气对负荷节点影响程度不一，远离发电机的节点更易受天气状态影响。

[1] 熊小伏, 王建, 袁峻, 等. 时空环境相依的电网故障模型及在电网可靠性评估中的应用[J]. 电力系统保护与控制, 2015, 43(15): 28-35.

XIONG Xiaofu, WANG Jian, YUAN Jun, et al. Temporal and spatial environments dependent power grid failure method and its application in power grid reliability assessment[J]. Power System Protection and Control, 2015, 43(15): 28-35.

[2] 薛禹胜, 吴勇军, 谢云云, 等. 停电防御框架向自然灾害预警的拓展[J]. 电力系统自动化, 2013, 37(16): 18-26.

XUE Yusheng, WU Yongjun, XIE Yunyun, et al. Extension of blackout defense scheme to natural disasters early- warning[J]. Automation of Electric Power Systems, 2013, 37(16): 18-26.

[3] 丁明, 戴仁昶, 洪梅, 等. 影响输电网可靠性的气候条件模拟[J]. 电力系统自动化, 1997, 21(1): 18-20.

DING Ming, DAI Renchang, HONG Mei, et al. Simulation to the weather condition affecting the reliability of transmission network[J]. Automation of Electric Power Systems, 1997, 21(1): 18-20.

[4] IEEE Standard 346:1973, terms for reporting and analyzingoutages of electrical transmission and distribution facilities and interruptions to customer services[S].

[5] BILLINTON R, SINGH G D. Reliability assessment of transmission and distribution systems considering repair in adverse weather conditions[C] // Proceedings of the 2002 IEEE Canadian conference on electrical and computer engineering. Vol 1. Piscataway (NJ): IEEE, 2002: 83-93.

[6] BILLINTON R, SINGH G D. Application of adverse and extreme adverse weather: modeling in transmission and distribution system reliability evaluation[J]. IEE Proc Gener, Transm, and Distrib, 2006, 153(1): 115-120.

[7] 郭静丽, 王秀丽, 侯雨伸, 等. 基于改进FD 法的柔性直流输电系统可靠性评估[J]. 电力系统保护与控制, 2015, 43(23): 8-13.

GUO Jingli, WANG Xiuli, HOU Yushen, et al. Reliability assessment of the VSC-HVDC transmission system based on a modified FD method[J]. Power System Protection and Control, 2015, 43(23): 8-13.

[8] 赵洪山, 赵航宇. 考虑元件故障率变化的配电网可靠性评估[J]. 电力系统保护与控制, 2015, 43(11): 56-62.

ZHAO Hongshan, ZHAO Hangyu. Distribution system reliability analysis considering the elements failure rate changes[J]. Power System Protection and Control, 2015, 43(11): 56-62.

[9] 何剑, 程林, 孙元章, 等. 条件相依的输变电设备短期可靠性模型[J]. 中国电机工程学报, 2009, 29(7): 39-46.

HE Jian, CHENG Lin, SUN Yuanzhang, et al. Condition dependent short-term reliability models of transmission equipments[J]. Proceedings of the CSEE, 2009, 29(7): 39-46.

[10] 邹欣, 孙元章, 程林. 基于模糊专家系统的输电线路非解析可靠性模型[J]. 电力系统保护与控制, 2011, 39(19): 1-6.

ZOU Xin, SUN Yuanzhang, CHENG Lin. Non-analytic reliability model of transmission lines based on fuzzy expert system[J]. Power System Protection and Control, 2011, 39(19): 1-6.

[11] 胡启洲, 张卫华. 区间数理论的研究及其应用[M]. 北京: 科学出版社, 2010.

[12] ZHANG Peng, WANG Haizhen. Interval mathematics based large-scale distribution system reliability analysis[C] // Proceedings of IEEE PowerCon2002. Kunming, China, 2002: 2526-2531.

[13] 任震, 万官泉, 黄雯莹. 参数不确定的配电系统可靠性区间评估[J]. 中国电机工程学报, 2003, 23(12): 68-73.

REN Zhen, WAN Guanquan, HUANG Wenying. An interval approach to evaluation distribution system reliability with parameters uncertainty[J]. Proceedings of the CSEE, 2003, 23(12): 68-73.

[14] 郑彦芹, 娄北, 张鸿雁, 等. 基于区间数和价值理论的配电网可靠性评估[J]. 电力系统保护与控制, 2008, 36(18): 19- 23.

ZHENG Yanqin, LOU Bei, ZHANG Hongyan, et al. Reliability evaluation of distribution system based on interval data and value[J]. Power System Protection and Control, 2008, 36(18): 19-23.

[15] 张鹏, 王守相. 大规模配电系统可靠性评估的区间算法[J]. 中国电机工程学报, 2004, 24(3): 77-84.

ZHANG Peng, WANG Shouxiang. A novel interval method for reliability evaluation of large scale distribution system[J]. Proceedings of the CSEE, 2004, 24(3): 77-84.

[16] 史新红, 齐先军, 王治国. 基于UGF的发电系统区间可靠性评估及其仿射算法改进[J]. 合肥工业大学学报(自然科学版), 2014, 37(3): 286-291.

SHI Xinhong, QI Xianjun, WANG Zhiguo. Interval reliability estimation of power generating system based on UGF method and its modification by using affine arithmetic[J]. Journal of Hefei University of Technology (Natural Science Edition), 2014, 37(3): 286-291.

[17] 莫海勇. 基于最小路与区间运算相结合的配电系统可靠性[D]. 天津: 天津大学, 2007.

[18] 钟佑明, 吕恩琳, 王应芳. 区间概率随机变量及其数字特征[J]. 重庆大学学报(自然科学版), 2001, 24(1): 24-27.

ZHONG Youming, LÜ Enlin, WANG Yingfang. Interval probability random variable and its numerical characters[J]. Journal of Chongqing University (Natural Science Edition), 2001, 24(1): 24-27.

[19] 丁涛, 崔翰韬, 顾伟, 等. 基于区间和仿射运算的不确定潮流算法[J]. 电力系统自动化, 2012, 36(13): 51-55.

DING Tao, CUI Hantao, GU Wei, et al. An uncertainty power flow algorithm based on interval and affine arithmetic[J]. Automation of Electric Power Systems, 2012, 36(13): 51-55.

[20] 丁明, 李小燕, 毕锐, 等. 含VSC-HVDC的交直流混合发输电系统可靠性评估[J]. 电网技术, 2006, 32(16): 53-58.

DING Ming, LI Xiaoyan, BI Rui, et al. The reliability assessment of hybrid AC/DC power system including the VSC-HVDC[J]. Power System Technology, 2006, 32(16): 53-58.

[21] BILLINTON R, KUMAR S, CHOWDHURY N, et al. A reliability test system for educational purposes-basic data[J]. IEEE Transactions on Power Systems, 1989, 4(3): 1238-1244.

(编辑 周金梅)

Interval reliability evaluation and affine arithmetic of transmission network considering weather factors

LI Xiaoyan, DING Ming, QI Xianjun

(Provincial Laboratory of New Energy and Energy Conservation, Hefei University of Technology, Hefei 230009, China)

By taking into consideration the effect of uncertainty of failure rate and weather condition on reliability evaluation of power system, based on the piece-wise model of transmission line, this paper presents a new reliability assessment model based on the interval probability theory to solve the uncertainty problem. The method uses interval arithmetic and state enumeration method to calculate interval-valued reliability indices of IEEE-RBTS. Furthermore, a large overestimate of boundaries in the interval arithmetic can be improved by affine arithmetic. The result shows that the weather condition will affect the reliability evaluation of the transmission system greatly, and the reliability indices in form of interval number also give the size of the uncertain part, which proves the efficiency and validity of the proposed method. This work is supported by National Natural Science Foundation of China (No. 51007017).

weather factors; transmission network; reliability evaluation; interval probability; affine arithmetic

10.7667/PSPC151617

国家自然科学基金资助项目(51007017)

2015-09-10；

2016-01-14

李小燕(1979-)，女，通信作者，博士，讲师，主要研究方向为电力系统可靠性评估；E-mail:leexiaoyan2002@ 163.com丁 明(1956-)，男，教授，博士生导师，主要研究方向为电力系统规划及可靠性评估，新能源利用，微网仿真和控制等；E-mail: mingding56@126.com 齐先军(1977-)，男，副教授，硕士生导师，主要研究方向为电力系统规划及可靠性评估。E-mail: qxj_216@163.com