无证书强指定验证者多重签名

杜红珍，温巧燕



无证书强指定验证者多重签名

杜红珍1，温巧燕2

(1. 宝鸡文理学院数学与信息科学学院，陕西宝鸡 721013；2. 北京邮电大学网络与交换技术国家重点实验室，北京 100876)

为了满足在司法行政、电子政务等领域的应用需求，提出了无证书强指定验证者多重签名的概念和敌手模型，利用双线性对构造了第一个无证书强指定验证者多重签名方案，在计算双线性Diffie-Hellman问题和计算Diffie-Hellman问题假设下证明了该方案是存在性不可伪造的，而且该方案满足强指定验证者签名和多重签名应具备的性质。方案执行效率高，生成的指定验证者多重签名长度仅为160 bit，签名验证时需要的双线性对运算个数是固定的，仅需一个双线性对。所以，即使在计算资源与网络带宽受限的无线网络中方案也非常实用。

无证书公钥密码学；指定验证者多重签名；不可伪造性；双线性对

1 引言

2003年，Al-Riyami等[1]提出了无证书公钥密码学（CL-PKC, certificateless public key cryptography），CL-PKC性能优良，汲取了传统公钥密码体制和基于ID的密码体制的优点，因为它不需要附带证书来认证用户的公钥，从而去掉了维护证书的费用，同时又不存在密钥托管问题，所以对CL-PKC的研究很有理论意义和实际应用价值。目前已有很多的无证书加密、签名方案[2~8]被提出。

普通数字签名的验证权是不可控的，即只要有签名人的公钥就可以检验签名的有效性，但在有些环境如电子投招标、电子购物、电子拍卖和知识产权保护等应用中，签名人希望由自己指定签名验证者，从而控制签名的验证权。为了满足这种应用，Jakobsson等[9]提出了指定验证者签名（DVS, designated verifier signature）的概念。在文献[9]中，Jakobsson等还提出了强指定验证者签名（SDVS, strong designated verifier signature）。在一个SDVS方案中，签名验证时要用到指定验证者的私钥，所以除了签名人指定的验证者以外，其他人都不能验证签名的有效性。2003年，Steinfeld等[10]提出了广义指定验证者签名（UDVS, universal designated verifier signature）的概念，UDVS与SDVS的主要区别是：前者允许任何一个（普通）签名持有者（不一定是签名者本人）根据自己的意愿来指定签名验证者，再将该（普通）签名转化为指定验证者签名。而后者是签名人自己确定签名的验证者，再直接生成指定验证者签名。

目前，在CL-PKC下研究指定验证者签名的成果颇丰。2006年，Huang等[11]利用双线性对提出了第一个无证书SDVS方案。2008年，Chen等[12]构造了一个无证书SDVS方案，生成的签名长度可压缩到160 bit。He等[13]构造了一个无需双线性对的无证书SDVS方案。李继国等[14]提出了一个基于证书的SDVS方案，签名的长度仅160 bit。Ming等[15]给出了无证书UDVS的概念。Du等[16]提出了第一个高效的无证书指定验证者代理签名方案。Hafizul等[17]在CL-PKC下提出了一个广义指定验证者多重签名方案，然而，该方案缺陷较多，比如作者概念不清，误称他们提出了一个无证书强指定验证者多重签名方案，且方案不能抵抗恶意但被动KGC的攻击。2015年，张玉磊等[18]在CL-PKC下提出了一个广义指定验证者聚合签名方案，该方案生成的聚合签名长度为320 bit，签名验证需要的双线性对个数固定，仅需4个对，所以方案执行效率较高。

多重签名（MS, multi-signature）的概念由Itakura等[19]提出，MS是一种多方参与的特殊签名，允许多个签名人在同一个消息上进行签署，生成的多重签名的长度远小于每个人对的普通签名的长度之和，且的验证代价同样大大低于验证多个所需计算量。多重签名在电子政务、电子病历、蜂窝电话、电子射频技术、传感器等领域应用广泛。

随着新型网络形态和网络服务的出现，研究多方参与的特殊签名已成为密码学界一个新热点。本文在CL-PKC下将指定验证者签名与多重签名结合，提出了一种特殊签名——无证书强指定验证者多重签名（CL-SDVMS, certificateless strong designated verifier multi-signature），它允许多个用户对同一个消息生成多重签名，且该多重签名的有效性只有这多个用户指定的验证者才能验证，其他第三方都无法验证签名。与强指定验证者签名类似，一个安全的CL-SDVMS方案应该具备强壮性（第三方不可验证性）、不可伪造性、不可传递性和签名源的隐匿性。现实生活中，CL-SDVMS有很多应用场景，比如多个目击者想要向法官揭发某个犯罪嫌疑人，但为了防止遭到报复，目击者们就指定该法官为签名验证者，采用CL-SDVMS方案来检举犯罪嫌疑人，这样，只有该法官可以验证签名的有效性，从而相信签名的真实性。同时CL-SDVMS的不可传递性也使目击者得到保护，因为其他人不会相信签名是目击者生成而不是法官生成的。CL-SDVMS在司法行政如呈报减刑、假释等工作和电子政务等领域有很好的应用前景。

本文首先提出了CL-SDVMS的定义和安全模型，接着利用双线性对构造了第一个CL-SDVMS方案，该方案满足强壮性、不可伪造性、不可传递性和签名源的隐匿性。方案执行效率高，因为它是非交互的，且签名的验证仅需一个双线性对，另外，生成的指定验证者多重签名长度固定，不会随签名人数的增加而增长。

2 预备知识

1) 双线性对

2) 计算Diffie-Hellman(CDH)问题

3) 计算双线性Diffie-Hellman(CBDH)问题

迄今为止，CDH问题和CBDH问题仍是困难的。

3 CL-SDVMS方案的形式化定义和安全模型

3.1 CL-SDVMS方案的形式化定义

定义1 CL-SDVMS方案的参与实体：一个私钥生成中心（KGC），个签名用户和一个由这个用户指定的验证者。CL-SDVMS方案由以下6个算法构成。

1) 系统建立（Setup）算法：输入一个安全参数，输出系统主密钥和系统参数，该算法由KGC执行。

2) 部分私钥生成(Partial-Private-Key-Extract)算法：由KGC执行，输入、和身份, 返回用户的部分私钥。

3) 用户密钥生成(User-Key-Generate)算法：由用户执行，输入、，输出该用户的秘密值和公钥（x,Pk）。

6) 签名模拟(Simulation)算法：该算法由指定验证者执行，输入，,set=，，，指定验证者的部分私钥/秘密值（D,x），输出一个与个签名人生成的不可区分的签名副本。

3.2 CL-SDVMS方案的安全模型

在一个CL-SDVMS方案中，存在2种具备不同攻击力的敌手A1和A2。第一种敌手A1模拟恶意用户，他掌握用户的秘密值，可以替换任意用户的公钥，但不知道系统主密钥和用户的部分私钥。第2种敌手A2模拟的是恶意但被动（malicious-but- passive）KGC，他拥有系统主密钥并可以求出用户的部分私钥，但不知道用户的秘密值，且不能替换用户的公钥。

下面通过引入挑战者X和敌手A（A1或A2）之间的Game来模拟CL-SDVMS的不可伪造性安全模型。

1) Setup：X运行Setup算法生成系统主密钥和公开参数，秘密保存，将发送给A。如果A是第2种敌手A2，则发送和给A2。

2) Query：A可以适应性询问以下预言机。

Hash询问：当A询问任意一个散列函数值时，X输出相应的散列值给A。

Partial-Private-Key-Extract询问：输入，X返回部分私钥给A（此预言机仅针对A1，A2不需要询问该预言机，因为它知道用户的部分私钥）。

Sign询问：A输入签名者/指定验证者身份（ID,ID），公钥(Pk,Pk), 消息，身份集set，X运行Sign算法生成相应的部分签名，再返回给A。

Verify 询问：A输入签名者/指定验证者身份（ID,ID），公钥(Pk,Pk)，消息/签名（，），身份集set，X运行Verify算法判断的有效性，再输出“1”或“0”给A。

①如果A是第一种敌手A1，中至少有一个)和指定验证者没有提交给Partial-Private-Key-Extract预言机，且（，，）没有提交给Sign预言机，则A获胜；

②如果A是第2种敌手A2，中至少有一个)和指定验证者没有提交给Secret-Value-Extract预言机，且（，，）没有提交给Sign预言机，则A获胜。

定义2 如果不存在概率多项式时间敌手A(A1或A2)在以上Game中能以不可忽略的优势获胜，则一个CL-SDVMS方案在适应性选择消息攻击下是存在性不可伪造的（EUF-CL-SDVMS-CMA2安全）。

4 一个高效的无证书强指定验证者多重签名方案

4.1 基本方案

本节构造了一个无证书强指定验证者多重签名方案，由下面6个算法组成。

5) 验证算法：输入，，，指定验证者ID(其部分私钥D=sQ，秘密值x)计算如下。

6) 签名模拟算法：对消息，指定验证者ID可以生成有效的指定验证者多重签名副本。

下面给出方案正确性的证明。

4.2 方案的安全性分析

4.2.1 不可伪造性

定理1 在Random Oracle模型和CBDH及CDH难题假设下，本文的CL-SDVMS方案在2类敌手A1和A2的攻击下是EUF-CL-SDVMS-CMA2安全的。

定理1由引理1和引理2推出。

引理1 在Random Oracle模型下，假定有敌手A1在概率多项式时间内以优势攻破了本文CL-SDVMS方案，记A1最多询问Create-User，Partial-Private-Key-Extract，Sign和Verify的次数分别为、、和，则存在一个算法X，使用A1为黑盒子，在时间内，以的优势解决CBDH难题，是1群上一个标量乘时间，是一个双线性对运算时间，inv是计算Z*上一个求逆时间。

证明 本CL-SDVMS方案涉及个签名用户和一个由这个用户指定的验证者ID，不妨假设除用户以外，其余−1个用户都被敌手A1贿赂（本文赋予了敌手更强的攻击能力，此处模拟的是一种极端情形，实际场景中一般不少于一个诚实者）。设X为挑战者，给定群上CBDH问题的任意实例，其中，,,未知，X最终目的是输出值。

Create-user：A1输入，X调出列表查看，如果用户已被创立，X只需将的公钥Pk返回给A1；否则，X执行如下。

Partial-Private-Key-Extract：当A1输入（以下默认用户已被创立），X调出列表，如果，则返回、；否则，停止模拟，输出failure。

Public-Key-Replace：当A1输入()进行公钥替换询问，X调出列表，用替换Pk，即Pk=再替换对应的秘密值。

Secret-Value-Extract：A1输入，X调出列表,返回给A1。

Sign：A1输入签名者/指定验证者的身份（ID,ID）和公钥(Pk,Pk), 消息，身份集set，X执行如下。

1) 如果ID≠ ID,ID时，X调出列表list()、列表list和列表list，计算，返回指定验证者签名给A1。

Verify：A1输入签名者/指定验证者的身份（ID,ID）和公钥(Pk,Pk)、消息/指定验证者签名（，）、身份集set，验证如下。

Forgery：最后，敌手A1伪造了一个在消息上关于的有效指定验证者多重签名*，其中，个签名者的身份/公钥为（）），指定验证者身份/公钥为（）。若和，则X停止模拟，输出failure；否则，，且，下面不妨假设I=。

从而，X可以计算

即X可以解决CBDH难题，但目前CBDH问题是困难的，所以规约出本文方案是EUF-CL-SDVMS- CMA2安全的。

下面计算X成功的概率。用E1、E2、E3、E4、E5表示5个事件如下。

1) E1：X回答A1的询问时没有失败。

2) E2：X回答A1的询问时没有失败。

3) E3：X回答A1的询问时没有失败。

4) E4：A1成功地伪造了1个在消息上的指定验证者多重签名*，其中，个签名者的身份为，指定验证者身份为。

5) E5：在发生情况下，有和。

显然，

则

当事件E1、E2、E3、E4、E5都发生时，X获胜，其概率为。

将X在Game中每次应答时进行的运算时间加起来可得

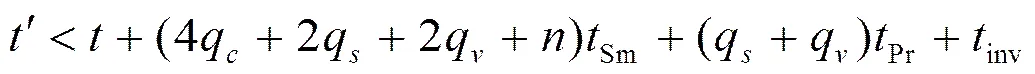
引理2 在Random Oracle模型下，假定有敌手A2在概率多项式时间内以优势攻破了本文CL-SDVMS方案，记A2最多询问Create-User、Secret-Value-Extract、Sign和Verify的次数分别为、、和，则存在一个算法X，使用A2为黑盒子，在时间内，以的优势解决CDH难题，是G1群上一个标量乘时间，是一个双线性对运算时间。

Create-user：A2输入，X调出列表查看，如果用户已被创立，A只需将的公钥Pk返回给A2；否则，X选2个随机数，计算，，用户的部分私钥，。接着计算用户的公钥如下。

Secret-Value-Extract：A2输入，如果，X调出列表，返回给A2；否则，输出failure。

Sign：A2输入签名者/指定验证者的身份（ID,ID）和公钥(Pk,Pk), 消息，身份集set，X调出列表()、列表和列表list，计算，返回指定验证者签名给A2。

Verify：A2输入签名者/指定验证者的身份（ID,ID）和公钥(Pk,Pk), 消息/指定验证者签名（，）、身份集set，X调出列表()、列表和列表list，检验，如果等式成立则返回“1”，表示签名有效；否则，返回“0”，说明签名无效。

Forgery：最后，敌手A2伪造了一个在消息上关于的有效指定验证者多重签名，其中，个签名者的身份/公钥为（）），指定验证者身份/公钥为（），若和，则X停止模拟，输出failure；否则，，且，下面不妨假设ID=。X调出列表或list，查看记录或，如果或list中没有这样的记录，则失败退出；否则，就有，从而X得到值，即X可以解决CDH难题，但目前CDH问题仍是困难的，所以，可规约为本文方案在A2攻击下是EUF-CL- SDVMS-CMA2安全的。另外，X成功的概率计算方法与引理1的相同，此处不再赘述。

4.2.2 强壮性（第三方不可验证性）

4.2.3 签名源隐匿性

签名源隐匿性是指给定一个消息/指定验证者多重签名对（,），即使第三方Coral知道个签名人和指定验证者ID的私钥，也不能判断出是ID还是ID生成的。

本文CL-SDVMS方案满足签名源隐匿性，下面对Coral赋予不同的攻击能力，分以下2种情况证明该性质。

1) Coral模拟敌手A：A拥有系统参数，签名人和指定验证者ID的公钥，且掌握−1个签名人ID的私钥（即部分私钥和秘密值。

2) Coral模拟敌手T：T除了具备A的攻击能力外，他还掌握所有签名人和指定验证者ID的私钥。

但是，如果用ID的私钥可以计算，其中，，。

综上，本文的CL-SDVMS方案满足签名源隐匿性。

4.2.4 不可传递性

不可传递性是指指定验证者ID虽然可以验证多重签名的有效性，但他不能使任何第三方相信就是个签名人所签，因为ID可以通过签名模拟算法生成与不可区分的签名副本。

显然，由签名源隐匿性可推出CL-SDVMS方案满足不可传递性。因为给定签名，即使第三方知道个签名人和指定验证者ID的私钥，也不能判断出是ID还是ID生成的，所以，如果指定验证者ID给他出示时，他不能相信就是所签。

4.3 方案的性能分析

Hafizul Islam SK方案[17]是一个无证书广义指定验证者多重签名方案，与本文方案最为接近，所以将本文CL-SDVMS方案与文献[17]方案进行了比较，如表1所示。其中，Sm、Pr分别表示群G1上1次标量乘计算、1次双线性对计算，其他运算耗时较短，此处忽略不计。

表1 方案性能比较（共n个签名用户）

4.3.1 效率分析

由于双线性对计算最昂贵，1次双线性对计算耗时至少是标量乘计算时间的20倍以上[20],即1（、分别表示一个双线性对运算与一个标量乘运算时间），则本文方案签名和验证的计算总时间量为，文献[17]方案的计算总时间量为。显然，，如取签名人数=5，则本文方案的签名和验证总耗时是文献[17]方案的56.1%。

另外，本文生成的签名长度为160 bit，文献[17]方案为320 bit，即本文方案传输签名的带宽比文献[17]方案节省了50%。

综上，本文方案的计算与通信代价大大低于文献[17]方案。

4.3.2 安全性分析

1) 本文方案满足不可伪造性，但文献[17]方案不能抵抗恶意但被动的KGC的伪造攻击。

2) 本文方案是非交互的，即签名前或签名过程中都不需要参与方交互信息来生成签名。文献[17]方案是交互的，在签名生成过程中需要每个签名人给其他签名人广播信息，且只有收到其他签名人的广播信息后才可以继续实施签名，这种交互的方案实用性不好。

由1)和2)可见，本文方案是一个性能良好的安全高效的CL-SDVMS方案。

5 结束语

CL-SDVMS在司法行政如呈报减刑、假释等工作和电子政务等领域有很好的应用前景。本文提出了第一个非交互、紧凑的CL-SDVMS方案，经证明方案满足强壮性、不可伪造性、不可传递性和签名源隐匿性。另外，该方案的实施所需计算量与通信量都很小，非常适合计算资源、网络带宽受限的新型无线网络环境。接下来的工作是构造无需双线性对的高效CL-SDVMS方案。

[1] AL-RIYAMI S, PATERSON K G. Certificateless public key cryptography[C]//ASIACRYPT 2003, LNCS 2894, Springer-Verlag.c2003: 452-473.

[2] YUM D H, LEE P J. Generic construction of certificateless encryption[C]//ICCSA 2004. LNCS 3043, Springer-Verlag, c2004:802-811.

[3] HE D B, HUANG B, CHEN J H. New certificateless short signature scheme[J]. Information Security IET, 2013, 7(2):113-117.

[4] YUAN Y, WANG C. Certificateless signature scheme with security enhanced in the standard model [J]. Information Processing Letters, 2014, 114, 492-499.

[5] DU H Z, WEN Q Y. Security analysis of two certificateless short signature schemes [J]. IET Information Security, 2014, 8(4): 230-233.

[6] CHEN Y C, TSO R, HORNG G, et al. Strongly secure certificateless signature: cryptanalysis and improvement of two schemes [J]. Journal of Information Science and Engineering, 2015, 31: 297-314.

[7] YEH K H, TSAI K Y, FAN C Y. An efficient certificateless signature scheme without bilinear pairings[J]. Multimed Tools Appl. Doi: 10.1007/s11042-014-2154-4.

[8] SEO S H, NABEEL M, DING X Y, et al. An efficient certificateless encryption for secure data sharing in public clouds[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(9):2107-2119.

[9] JAKOBSSON M, SAKO K, IMPAGLIAZZO R. Designated verifier proofs and their applications[C]//Advances in Cryptology-Eurocrypt 1996. LNCS 1070, Berlin, Springer-Verlag, c1996: 142-154.

[10] STEINFELD R, BULL L, WANG H, PIEPRZYK J .Universal designated verifier signatures[C]//Advanced in Asiacrypt’03, Berlin: Springer-Verlag, c2003: 523-542.

[11] HUANG X Y, SUSILO W, MU Y and ZHANG F T. Certificateless designated verifier signature schemes[C]//SNDS 2006, IEEE Computer, c2006: 15-19.

[12] CHEN H, SONG R S, ZHANG F T, et al. An efficient certificateless short designated verifier signature scheme[C]//WiCOM, IEEE, c2008: 1-6.

[13] HE D B, CHEN J H. An efficient certificateless designated verifier signature scheme[J]. International Arab Journal of Information Technology, 2013, 10(4): 389-396.

[14] 李继国, 钱娜, 黄欣沂, 等. 基于证书强指定验证者签名方案[J]. 计算机学报, 2012, 35(8): 1579-1587.

LI J G, QIAN N, HUANG X Y，et al. Certificate-based strong designated verifier signature scheme[J]. Chinese Journal of Comupters, 2012, 35(8): 1579-1587.

[15] MING Y, SHEN X Q, WANG Y M. Certificateless universal designated verifier signature schemes[J]. The Journal of China Universities of Posts and Telecommunications, 2007,14(3): 85-90.

[16] DU H Z, WEN Q Y. Efficient certificateless designated verifier signatures and proxy signatures[J]. Chinese Journal of Electronics, 2009, 18(1): 95-100.

[17] HAFIZUL I S, BISWAS G P. Certificateless strong designated verifier multisignature scheme using bilinear pairings[C]//International Conference on Advances in Computing, Communications and Informatics. c2012: 540-546.

[18] 张玉磊, 周冬瑞, 李臣意, 等. 高效的无证书广义指定验证者聚合签名方案[J]. 通信学报, 2015, 36(2): 1-8.

ZHANG Y L, ZHOU D R, LI C Y, et al. Efficient certificateless aggregate signature scheme with universal designated verifier[J]. Journal on Communications, 2015, 36(2): 1-8.

[19] ITAKURA K and NAKAMURA K. A public-key cryptosystem suitable for digital multisignatures[J]. NEC Research and Development, 1983, (71):1-8.

[20] CHEN L, CHENG Z, SMART N P. Identity-based key agreement protocols from pairings[J]. International Journal of Information Security, 2007, 6(4): 213-241.

Certificateless strong designated verifier multi-signature

DU Hong-zhen1, WEN Qiao-yan2

(1. School of Mathematics and Information Science, Baoji University of Arts and Sciences, Baoji 721013, China; 2. State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing 100876, China）

In order to satisfy the application requirements in the fields of judicial administration, e-government, etc., the definition and security model for certificateless strong designated verifier multi-signature were proposed. Then, the first certificateless strong designated verifier multi-signature scheme from bilinear pairings was constructed and it was proved that the scheme is existentially unforgeable under the computational bilinear Diffie-Hellman assumption and the computational Diffie-Hellman assumption. Moreover, the scheme meets the properties of both strong designated verifier signatures and multi-signatures. The scheme achieves high efficiency since the length of designated verifier multi-signature generated by the scheme is only 160 bits and the computational cost of bilinear pairings necessary for verification algorithm is constant, i.e., one bilinear pairing. So, it can be applied in wireless networks of the limited computing resources and network bandwidth.

certificateless public key cryptography, designated verifier multi-signature, unforgeability, bilinear pairing

TP309

A

10.11959/j.issn.1000-436x.2016112

2015-12-27；

2016-05-11

国家自然科学基金资助项目（No.61402015, No.61402275）；陕西省教育厅专项科研基金资助项目（No.15JK1022）；陕西省自然科学基础研究基金资助项目（No.2015JM6263）

The National Natural Science Foundation of China (No.61402015, No.61402275), The Scientific Research Project of Shaanxi Provincial Educations Department (No.15JK1022), The Basic Research Project of Natural Science in Shaanxi Province (No.2015JM6263)

杜红珍（1978-），女，陕西扶风人，博士，宝鸡文理学院副教授，主要研究方向为密码学、物联网安全和数字签名技术。

温巧燕（1959-），女，陕西西安人，北京邮电大学教授、博士生导师，主要研究方向为密码学与信息安全。