颗粒级配对粗骨料充填料浆离析的影响

吴爱祥，王建栋，彭乃兵



颗粒级配对粗骨料充填料浆离析的影响

吴爱祥1, 2，王建栋1, 2，彭乃兵1, 2

(1. 北京科技大学金属矿山高效开采与安全教育部重点实验室，北京，100083；2. 北京科技大学土木与环境工程学院，北京，100083)

基于不合理的颗粒级配是粗骨料充填料浆发生离析的重要因素，以富勒公式为基础，建立平均粒径和粒径分散系数2个级配表征参数。基于魏茅斯干涉级配理论设计11种颗粒级配，并以此进行离析实验确定粒径分散系数的合理范围，利用云南某矿固体物料进行室内验证实验。研究结果表明：以屈服应力175~225 Pa、膏体料浆粒度低于20 μm颗粒质量分数为约束条件，可得当粗骨料充填料浆合理离析率为11.65%~14.53%时，其粒径分散系数为1.43~1.45，平均粒径为1.89~2.00 mm；基于原级配的优化调整必要且有效；料浆质量分数为68%的3和质量分数为70%的2离析率测量值与合理离析率相比，误差分别为3.23%和5.75%，粗骨料充填料浆粒径分散系数和平均粒径的范围可靠、准确。

颗粒级配；粗骨料；离析率；粒径分散系数

废石、水淬渣等固体废弃物是矿山废渣的重要组成部分。矿山在充填料浆中加入上述粗骨料，不仅可以提高固体废弃物的综合利用率，减少其地表堆存造成的占地和环境污染等问题，而且可提高充填体强度，改善充填料浆的流动性[1]。但充填料浆中骨料离析所导致的堵管、充填体分层等现象时有发生，不合理的颗粒级配则是导致料浆离析的重要因素之一[2−3]。长期以来，国内外学者对颗粒级配的理论和设计方法进行了大量的研究。SCHLANGEN等[4−5]分析了富勒最大密度曲线，认为颗粒级配曲线越接近抛物线，密度越大；张爱勤等[6−7]介绍了泰波理论，认为最大密度受泰波递减指数的影响而存在一定范围的波动；刘晏荣等[8−9]阐述了魏茅斯粒子干涉理论，认为要达到最大密度，颗粒间的空隙应由次一级颗粒填充，剩余空隙又由再次一级颗粒填充，并且填充空隙的颗粒粒径不得大于其间隙的距离，否则不同粒度的颗粒间会发生干涉现象；林绣贤[10]推广最大密度理论，提出了以通过百分率的递减率为参数、能应用于实际工程的理论式等。目前，人们对有关级配对粗骨料充填料浆离析的影响研究很少，大部分研究只针对混凝土领域。为此，本文作者拟建立颗粒级配的表征参数，结合理论级配设计和离析实验，分析颗粒级配对粗骨料充填料浆离析的影响规律，以便为不同粒径粗骨料在充填采矿中的合理配比提供参考。

1 颗粒级配设计

1.1 设计原理

以魏茅斯干涉级配理论为基础，通过计算次级粒径颗粒的实积率设计骨料连续级配。当前一级颗粒间隙距离等于次一级颗粒粒径时，骨料组成体系即处于理想临界状态，计算公式为

式中：为次一级颗粒粒径，连续级配时，=0.5；为前一级颗粒粒径；为次一级颗粒的实用实积率，即分计筛余百分率；为次一级颗粒的理论实积率，即堆积密度与表观密度之比。级配设计时，先测量每一级颗粒的堆积密度和表观密度，并据此计算该粒级颗粒的理论实积率和实用实积率，得到各级骨料的分计筛余百分率[11]，从而制配符合实验要求的粗骨料。

1.2 参数表征

累积筛余百分率表和粒度分布曲线能够很好地反映某一集料的粒径分布情况，但其缺点是数据繁多且分散。若以颗粒级配作为具体物理量来进行分析，则需要建立能够表征颗粒级配的若干参数。由于实验所用骨料级配是基于式(1)设计的，其理想临界状态可达到最大密度，用富勒公式对设计的级配进行函数拟合：

式中：d为某筛孔尺寸；max为集料的最大粒径；T为颗粒粒径d的通过率，%；和均为拟合系数。以式(2)作为颗粒粒径的分布函数()，对()求导可得颗粒粒径的概率密度函数()。对于集料体中的某一粒径，其在任意粒径区间[，]的分布概率为[12]

基于式(4)，借鉴概率统计标准差的算法，建立集料体粒径分散系数的计算公式：

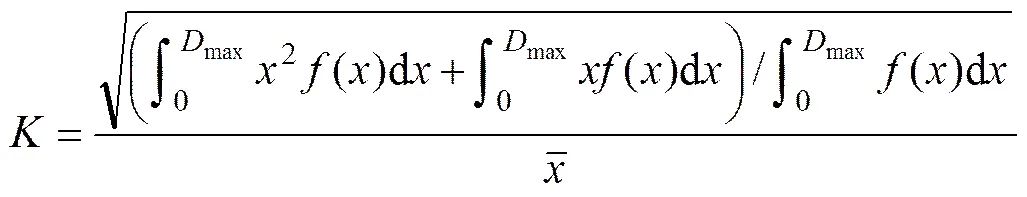
由式(4)和式(5)可知：平均粒径和分散系数能够体现集料体中任意颗粒粒径和分布规律，适合表征颗粒级配。

2 实验

2.1 实验材料

实验所用材料主要有全尾砂、胶结剂和粗骨料。全尾砂来自新疆某铜矿，其中粒度小于20 μm的极细颗粒质量分数为31.6%，粒度小于74 μm的颗粒质量分数为64.32%；胶结剂采用早强型复合硅酸盐水泥(P.C32.5R)；粗骨料源于矿山碎石，根据国家标准GB6003—85“实验筛”的筛孔尺寸[13]，配制最大粒度分别为4.75，9.50和16.00 mm这3种粒级的粗集料。

2.2 实验装置

本次实验装置以改进的混凝土捣实系数仪为主，如图1所示。将搅拌均匀的粗骨料充填料浆倒入漏斗，1 min后，使浆体自由落入到底部高420 mm、长和宽均为100 mm的模具中[14]。浆体填满模具后，不经捣实或振动，静置7 d后拆模，用刀具沿着试块高的方向将充填体试样平均切割成两半。同时，为减少实验误差，每组实验进行3次取平均值。

图1 离析实验装置

2.3 实验方案

2.3.1 粗集料配制

针对最大粒径为4.75 mm的粗集料设计5种不同的颗粒级配，将式(1)的计算结果作为标准实用实积率，并以此配制第1种级配1，其余几种级配的实用实积率在标准实用实积率的基础上增减：2的实积率减0.05，3的实积率减0.08，4的实积率加0.05，5的实积率加0.08。

同理，根据最大粒径为9.5 mm粗集料的标准实用实积率配制6，实积率在标准实用实积率的基础上减0.05得7，加0.05得8。最大粒径为16 mm粗集料的配制方案与前面的相同，可得到9，10和11这3种级配。按要求配制完成后，通过筛分实验测量11种粗集料的实际级配，结果如表1所示。

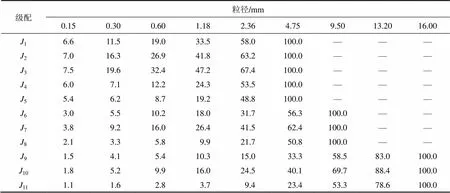
表1 粗集料级配(通过率)

2.3.2 料浆屈服应力测定

屈服应力与充填料浆的离析率成负相关，即屈服应力越大，浆体内部颗粒离析程度越小[15−17]。按照魏茅斯理论，若次一级颗粒不能完全填充前一级颗粒的空隙，则粗集料骨架结构无法达到最大密实，也就体现在浆体易被搅动，屈服应力降低。为确定充填料浆的合理离析范围，需建立颗粒级配、料浆屈服应力和离析率三者之间的关系。

实验采用Brookfield R/S plus型浆式流变仪测定每组充填料浆的屈服应力，料浆的参数设置均相同(不包括颗粒级配)：质量分数为68%，灰砂比为0.1，全尾砂与粗集料的质量比(简称尾碎比)为2。

2.3.3 离析率测定

将实验切割出的试块横截面水平等分成6份(如图1所示)，并分离出每份中颗粒粒径大于1 mm的粗骨料称质量，据此计算粗骨料充填料浆的离析率：

式中：M为每一等份中粒度大于1 mm的粗骨料质量，g；为试块中粒度大于1 mm的粗骨料平均质量，g；为粗骨料充填料浆的离析率，%。

2.4 实验结果

不同级配的充填料浆均进行3次实验，所测离析率取平均值，实验结果见表2。

表2 实验结果

3 结果分析

3.1 级配表征参数计算

根据表1数据绘制不同级配的粒度分布曲线，利用式(2)对曲线进行拟合，可确定不同级配的概率密度函数，从而求得不同级配相对应的平均粒径和粒径分散系数。以级配9为例，其粒度分布曲线和拟合曲线如图2所示。

1—级配J9的粒度分布曲线；2—拟合曲线。

结合式(2)和拟合曲线可得9颗粒粒径的分布函数：

由式(8)可得9的平均粒径为7.73 mm，粒径分散系数为1.22。同理，其余各级配的平均粒径和粒径分散系数如表3所示。

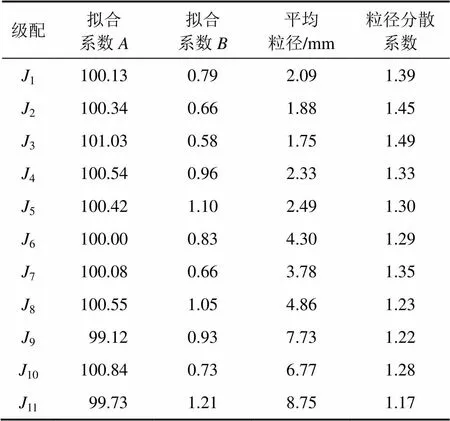
表3 粗集料平均粒径和粒径分散系数

3.2 料浆屈服应力对离析率的影响

根据表2中数据绘制粗骨料充填料浆屈服应力和离析率之间的关系曲线，如图3所示。

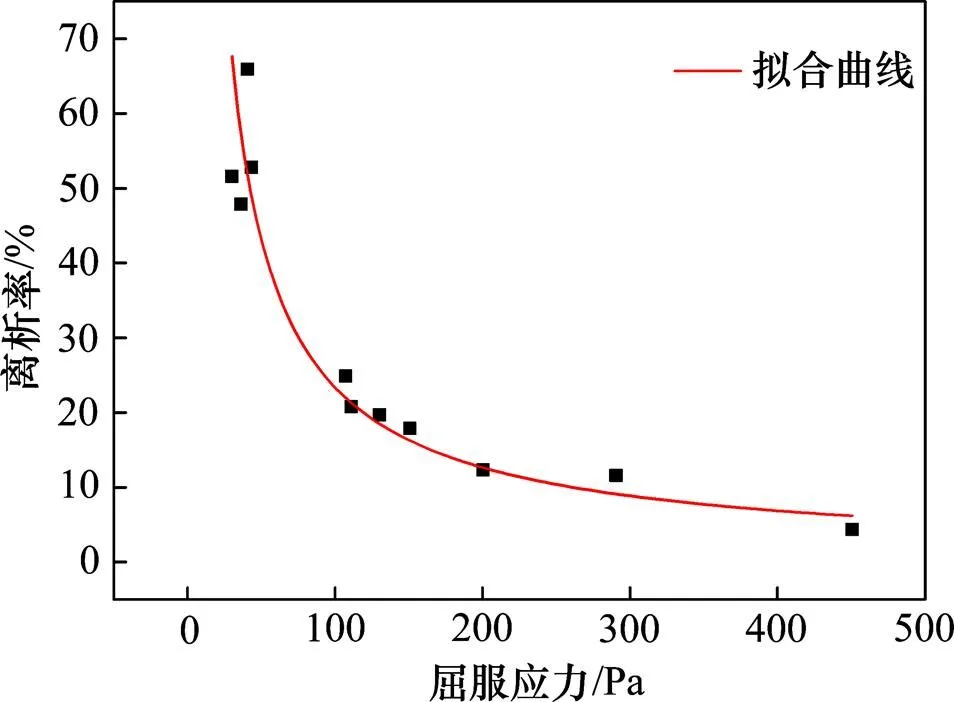
图3 料浆屈服应力与离析率关系

采用Allometric模型对图3中的关系曲线进行拟合，回归方程为

式中：为充填料浆的离析率，%；1为粗骨料充填料浆的屈服应力，Pa；复相关系数2=0.849。

充填料浆完全不离析是无法实现的，对于粗骨料混凝土而言，其振动离析率应小于等于10%[18−19]，但并没有衡量充填料浆抗离析性能的离析率控制值。当充填料浆达到不离析的膏体状态时，其中粒度小于 20 μm颗粒的质量分数约为20%，屈服应力为(200±25) Pa[20−23]。但过大的屈服应力也会导致浆体自流性差，工程应用难[24]。本文以屈服应力175~225 Pa作为充填料浆合理离析率的控制条件，将屈服应力范围临界值代入式(9)，可得粗骨料充填料浆拥有的合理离析率范围为11.65%~14.53%。

3.3 粒径分散系数对离析率的影响

结合表2和表3的数据绘制粗集料粒径分散系数和料浆离析率的关系曲线，如图4所示。

图4 粒径分散系数与离析率关系

对粒径分散系数和离析率两者之间的关系进行回归，最终回归方程为

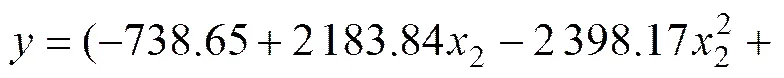
式中：为充填料浆的离析率，%；2为级配的粒径分散系数；复相关系数2=0.938。

结合图4和式(10)可知：充填料浆离析率并不随粒径分散系数的变化而单调增减，而是当处于某一临界值时，离析率最小。同时，据图4中虚线与拟合曲线的交点可初步确定：当满足合理离析率范围为11.65%~14.53%时，此级配范围对应的的范围为[1.35, 1.37][1.43, 1.45]。

当实验料浆质量分数为68%，灰砂比为0.1，尾碎比为2以及全尾砂中粒度小于20 μm的颗粒质量分数为31.6%时，全尾砂为整个料浆体系贡献了19.22%粒度小于20 μm的颗粒。为使膏体料浆粒度低于20 μm的颗粒质量分数达到20%，粗集料还需提供剩余的0.78%粒度小于20 μm的颗粒，则粗集料自身粒度小于20 μm的颗粒质量分数为2.57%。根据式(2)和表3中的拟合系数，可计算不同级配粗集料中粒度小于20 μm的颗粒质量分数，见表4。

表4 不同级配粗集料粒度小于20 μm的颗粒质量分数

由表4可知：级配介于1和2之间，才能满足粒度小于20 μm的颗粒质量分数为2.57%，此级配范围对应的粒径分散系数范围为1.39~1.45，结合满足合理离析率的范围为[1.35, 1.37][1.43, 1.45]，可最终确定：当粗骨料充填料浆达到膏体状态、合理离析率为11.65%~14.53%时，其所含粗集料粒径分散系数为1.43~1.45，平均粒径为1.89~2.00 mm。

3.4 室内实验验证

3.4.1 实验材料

选择云南某矿制备充填料浆的基本物料(主要包括最大粒径为5 mm的粗集料、全尾砂和水泥)进行室内验证实验，该矿所用粗集料的原有级配1见表5。

表5 云南某矿粗集料级配

根据表5中的级配数据，拟合和计算得该矿所用粗集料的平均粒径为2.50 mm，粒径分散系数为1.32。将式(2)代入式(4)和(5)可得：

调节平均粒径和粒径分散系数使其分别满足前面所求的约束范围，则可取0.65和0.66，由表3可知拟合系数约为100，则可据此调整出满足约束范围的2种级配2和3，其平均粒径分别为1.97 mm和1.99 mm，粒径分散系数分别为1.44和1.45。2种级配的累积筛余百分率见表6。

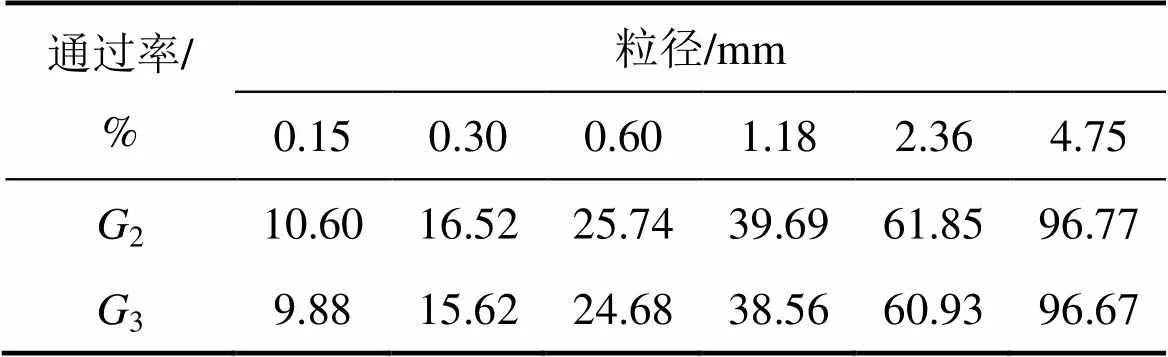
表6 调整后的粗集料级配

3.4.2 实验测定

配制质量分数为68%，69%和70%，灰砂比均为0.1，尾碎比均为2的充填料浆，不同质量分数的料浆均采用上述3种级配，分别进行离析实验，离析率实验结果如表7所示。

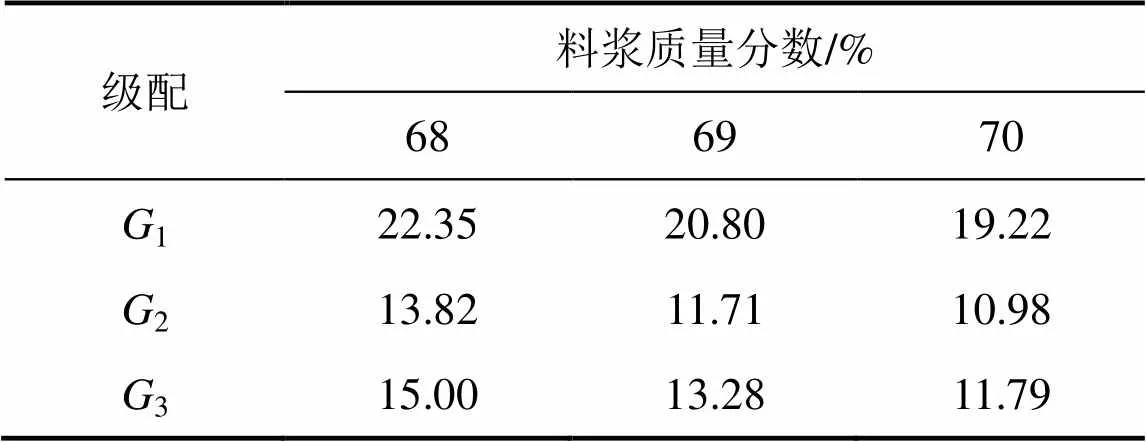
表7 离析率实验结果

3.4.3 验证结果

由表7可知：随着充填料浆质量分数增加，料浆离析率有所减小，但室内验证实验所选取的料浆质量分数已经达到膏体的临界值，再增大质量分数会提高矿山的充填成本，所以，上述3种质量分数下的离析率可为现场充填提供一定参考。

以质量分数为68%的料浆为例，该矿山原有级配1的离析率高达22.35%，而2和3的离析率只有13.82%和15.00%，离析率明显降低，表明级配调整必要且有效。而在这3种质量分数下，质量分数为68%的3离析率为15.00%，质量分数为70%的2离析率为10.98%，与合理离析率11.65%~14.53%相比，误差分别为3.23%和5.75%。

4 结论

1) 将富勒公式作为粗集料颗粒粒径的分布函数，并以此建立颗粒级配的表征参数：平均粒径和粒径分散系数。这表明参数能够反映集料体中任意颗粒粒径和分布规律，适合表征颗粒级配。

2) 以屈服应力175~225 Pa作为边界条件，可得粗骨料充填料浆的合理离析率为11.65%~ 14.53%。根据粒径分散系数与充填料浆离析率的关系拟合方程，结合合理离析率反推得粒径分散系数的初始范围。

3) 以料浆中粒度小于20 μm颗粒质量分数为约束条件，最终确定粒径分散系数的取值：当粗骨料充填料浆达到膏体状态、满足合理离析率范围时，其所含粗集料粒径分散系数为1.43~1.45，平均粒径为1.89~2.00 mm。

4) 采用云南某矿固体物料进行室内实验验证，结果表明基于原级配的优化调整必要且有效；质量分数为68%的3离析率、质量为70%的2离析率与合理离析率范围相比，误差分别为3.23%和5.75%。

[1] 王洪江, 吴爱祥, 肖卫国, 等. 粗粒级膏体充填的技术进展及存在的问题[J]. 金属矿山, 2009(11): 1−5. WANG Hongjiang, WU Aixiang, XIAO Weiguo, et al. The progresses of coarse paste fill technology and its existing problem[J]. Metal Mine, 2009(11): 1−5.

[2] 高丹盈, 汤寄予, 赵军. 骨架密实型沥青混合料矿料级配的设计与优化[J]. 公路, 2008(11): 190−195. GAO Danying, TANG Jiyu, ZHAO Jun. Design and optimization for gradation of skeleton densified asphalt mixture[J]. Highway, 2008(11): 190−195.

[3] 付长怀. 粗骨料对膏状浆体管输阻力的影响[J]. 黄金, 1995, 16(7): 20−23. FU Changhuai. The influence of the coarse aggregate on the resistance of pipeline transportation[J]. Gold, 1995, 16(7): 20−23.

[4] SCHLANGEN E, MIER J G M V. Simple lattice model for numerical simulation of fracture of concrete materials and structures[J]. Materials & Structures, 1992, 25(9): 534-542.

[5] LARRARD F D, SEDRAN T. Mixture-proportioning of high-performance concrete[J]. Cement & Concrete Research, 2002, 32(11): 1699−1704.

[6] 张爱勤. 泰波理论在矿料级配设计中的应用[J]. 山东建材学院学报, 2000, 14(2): 141−142. ZHANG Aiqin. Application of Talbol’s theory in grading design of sand and crushed rock mixture[J]. Journal of Shandong Institute of Building Materials, 2000, 14(2): 141−142.

[7] 彭浩. 基于骨料级配优化的混凝土配合比设计方法研究[D]. 北京: 北京建筑大学土木与交通工程学院, 2014: 5−6. PENG Hao. Research on concrete mixture design method based on aggregate gradation optimum[D]. Beijing: Beijing University of Civil Engineering and Architecture. School of Civil and Transportation Engineering, 2014: 5−6.

[8] 刘晏荣, 曹梦醒, 廖陈林. 级配理论的应用研究[J]. 山西建筑, 2007, 33(12): 165−167.LIU Yanrong, CAO Mengxing, LIAO Chenlin. Application and research of grade-suit theory[J]. Shanxi Architecture, 2007, 33(12): 165−167.

[9] 陈忠达, 袁万杰, 郑东启. 级配理论应用研究[J]. 重庆交通大学学报(自然科学版), 2005, 24(4): 44−48. CHEN Zhongda, YUAN Wanjie, ZHENG Dongqi. Study on the application of grading theory[J]. Journal of Chongqing Jiaotong University (Natural Science), 2005, 24(4): 44−48.

[10] 林绣贤.沥青混凝土合理集料组成的计算公式[J]. 华东公路, 2003(1): 82−84. LIN Xiuxian. A formula for reasonable aggregate composition of asphalt concrete[J]. East China Highway, 2003(1): 82−84.

[11] 刘金杰. 骨架密实型水泥碎石基层研究[D]. 石家庄: 河北工业大学土木与交通学院, 2007: 13−14. LIU Jinjie. Dense framework cement gravel grassroots re-search[D]. Shijiazhuang: Hebei University of Technology. School of Civil and Transportation Engineering, 2007: 13−14.

[12] 包秀宁, 张肖宁, 吴旷怀, 等. 级配对矿质颗粒体离析的影响研究及应用[J]. 中山大学学报(自然科学版), 2009, 48(6): 48−53. BAO Xiuning, ZHANG Xiaoning, WU Kuanghuai, et al. Research and application of the gradation impact on mineral granular masses segregation[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2009, 48(6): 48−53.

[13] JTG E42—2005,公路工程集料试验规程[S]. JTG E42—2005, Test methods of aggregate for highway engineering[S].

[14] BUI V K, MONTGOMERY D, HINCZAK I, et al. Rapid testing method for segregation resistance of self-compacting concrete[J]. Cement and Concrete Research, 2002, 32(9): 1489−1496.

[15] BERIS A N, TSAMOPOULOS J A, ARMSTRONG R C, et al. Creeping motion of a sphere through a Bingham plastic[J]. Journal of Fluid Mechanics, 1985, 158: 219−244.

[16] SAAK A W, JENNINGS H M, SHAH S P. New methodology for designing self-compacting concrete[J]. ACI Materials Journal, 2001, 98(6): 429−439.

[17] KOEHLER E P, FOWLER D W. Static and dynamic yield stress measurements of SCC[C]// Third North American Conference on the Design and Use of Self-consolidating Concrete. Chicago, USA: ACBM, 2008: 11.

[18] JGJ/T 282—2012,自密实混凝土应用技术规程[S]. JGJ/T 282—2012, Technical specification for application of self-compacting concrete[S].

[19] ASTM C1610/C1610M—10, Standard test method for static segregation of self-consolidating concrete using column technique[S].

[20] 吴爱祥, 刘晓辉, 王洪江, 等. 考虑时变性的全尾膏体管输阻力计算[J]. 中国矿业大学学报, 2013, 42(5): 736−740. WU Aixiang, LIU Xiaohui, WANG Hongjiang, et al. Calculation of resistance in total tailings paste piping transportation based on time-varying behavior[J]. Journal of China University of Mining & Technology, 2013, 42(5): 736−740.

[21] 王勇, 吴爱祥, 王洪江, 等. 深锥浓密机体积确定方法及其应用[J]. 中国矿业大学学报, 2013, 42(1): 45−49. WANG Yong, WU Aixiang, WANG Hongjiang, et al. A method to determine deep cone thickener volume and its application[J]. Journal of China University of Mining & Technology, 2013, 42(1): 45−49.

[22] FALL M, CELESTIN J, HAN F S. Potential use of densified polymer-paste fill mixture as waste containment barrier materials[J]. Waste Management, 2010, 30(12): 2570−2578.

[23] JEWELL R J, FOURIE A B. Paste and thickened tailings: a guide[M]. Perth: Australian Centre for Geomechanics (ACG), 2002: 27−30.

[24] 王勇, 吴爱祥, 王洪江, 等. 从屈服应力角度完善膏体定义[J]. 北京科技大学学报, 2014, 36(7): 855−860. WANG Yong, WU Aixiang, WANG Hongjiang, et al.Further development of paste definition from the viewpoint of yield tress[J]. Journal of University Science and Technology Beijing, 2014, 36(7): 855−860.

Effect of grain composition on coarse aggregate filling slurry segregation

WU Aixiang1, 2, WANG Jiandong1, 2, PENG Naibing1, 2

(1. Key Laboratory of High-Efficient Mining and Safety of Metal Mines, Ministry of Education, University of Science and Technology Beijing, Beijing 100083, China; 2. School of Civil and Environmental Engineering, University of Science and Technology Beijing, Beijing 100083, China)

Considering that unreasonable grain composition is an important factor of coarse aggregate filling slurry segregation, the representation parameters of gradation, i.e., averagegraindiameter and particle size distribution index, were established based on the Fuller formula. Eleven types of gradation based on Weymouth gradation theory were used for segregation test to study the range of particle size distribution index. Solid materials from a certain mine in Yunnan Province were used for verification test. The results show that, at constraint conditions, i.e. yield stress of 175−225 Pa and mass fraction of paste slurry with diameter of less than 20 μm, reasonable segregation rate of coarse aggregate filling slurry is from 11.65% to 14.53%. Particle size distribution index is from 1.43 to 1.45 and average grain diameter is from 1.89 mm to 2.00 mm. The optimization and adjustment of natural gradation is necessary and effective. Compared with reasonable segregation rate, the segregation rates of3with slurry mass fraction being 68% and2with 70% have a discrepancy of 3.23% and 5.75%, respectively. Hence, the ranges of particle size distribution index and averagegraindiameter determined in the paper are accurate and reliable.

grain composition; coarse aggregate; segregation rate; particle size distribution index

10.11817/j.issn.1672-7207.2016.09.039

TD853

A

1672−7207(2016)09−3201−07

2015−12−22；

2016−02−12

国家自然科学基金资助项目(51374034，51304011，51374035)；国家“十二五”科技支撑计划项目(2012BAB08B02) (Projects(51374034, 51304011, 51374035) supported by the National Natural Science Foundation of China; Project(2012BAB08B02) supported by the National “Twelfth Five-Year” Plan for Science & Technology of China)

吴爱祥，博士，教授，从事膏体充填采矿、矿山岩石力学、溶浸采矿等研究；E-mail:wuaixiang@126.com

(编辑 陈灿华)