土石坝漫顶溃坝模拟分析计算

李钦智

(新疆石河子市新疆玛纳斯河流域管理局， 新疆 石河子　832000)



土石坝漫顶溃坝模拟分析计算

李钦智

(新疆石河子市新疆玛纳斯河流域管理局， 新疆 石河子832000)

本文对土石坝的溃坝模式进行了简述，针对土石坝漫顶溃坝模拟分析的概化数学模型编制了计算程序，并结合大洼水库溃坝的工程实例进行数值模拟，与该工程实例的实测数据进行了比较分析，进一步说明土石坝漫坝计算过程中数学模型与假设对计算结果、精度、风险分析的重要性。

土石坝； 漫坝； 模型； 计算分析

1　引　言

随着中国经济的飞速发展，中国水利水电工程的建设也在讯速发展。据统计，目前中国的土石坝数量居世界首位，而中国土石坝的年溃坝概率也从以前远超世界其他国家逐渐转变为低溃坝率国家[1]。资料显示，土石坝的溃坝主要由两方面造成：ⓐ洪水等原因引起的漫坝，导致坝体坍塌破坏而造成溃坝；ⓑ坝基等渗透破坏，逐渐造成坝体渗漏最终导致土石坝的渗透溃坝。本文主要研究土石坝漫顶溃坝时溃口的流量过程变化。土石坝的溃决属于逐渐溃决，漫顶溃决时间可能持续若干小时，溃坝洪水流量逐步增大，至峰值流量后逐步减小。溃口洪水流量过程决定了对下游影响的范围和程度，通过对溃口形状的假设，用数学模型来概化描述溃口及洪水的发展过程，为实际工程中的洪水过程预测与风险分析提供依据。

溃坝的发生、发展和溃决程度等受到多种因素(如溃坝原因、坝体尺寸和材料、库容及下游水位等)影响，模拟难度非常大。尽管如此，在过去几十年中，中国在土石坝的溃坝模拟领域取得了相当大的进展，出现许多新的研究成果，如：溃口发展模式、溃决机理、大尺度物理模型实验成果等。土石坝溃决模型可分为两大类。第一类主要利用一些关键参数(如：溃口历时、溃口最终宽度等)，通过简单的时变过程(如：溃口尺寸的线性发展假设)模拟溃口的发展；还有一些模型通过建立库容等关键参数与溃口发展速度、最大溃坝洪水流量之间的回归方程来模拟溃坝过程。总的来说这类模型较简便，对数据输入要求较少，使用较方便，但由于未涉及实际的溃坝机理，精确度较低，故此类模型仅可用于初步计算。第二类模型通过结合水力学、泥沙、土力学等学科的综合知识构建一个时变过程以模拟实际的溃坝过程和溃坝洪水过程线，比较典型的有P-T模型、BEED模型和BREACH模型等[2]。

2　土石坝溃口概化模拟分析

2.1溃口流量概化过程及其验证

邓刚等[8]提出了基于假设的溃口流量概化模型，模型基于如下假设：ⓐ溃口形状假定为倒梯形；ⓑ以恒定值的材料冲刷速度作为溃口深度发展的控制指标；ⓒ假设溃口达到洪峰流量时溃口深度停止发展；ⓓ采用宽顶堰流量公式计算溃口流量。

考虑到溃口开始及溃坝结束时均存在一个渐进过程，即溃口流量增长并非在溃坝开始时就达到一定速度，而溃坝结束时，流量也是缓慢减小，直至与水库入流逐步达到一致，本文对上述模型[8]的假设进行了一定调整，将达到峰值前后的土石坝溃口流量过程线分别概化为不同的二次函数过程，以在继续保证模型简洁性的同时改善模型的数值特性，使溃坝流量过程线两端光滑可导，以便在分析中与原流量过程无缝连接。具体过程如下：

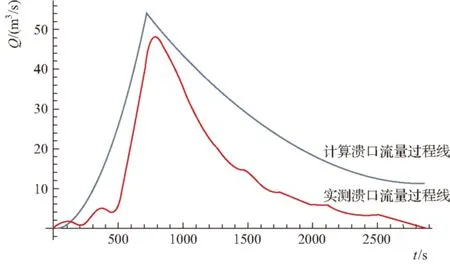
当0

(1)

当t1

(2)

设溃坝全过程中水库水量变化值为ΔV，则

(3)

即

(4)

全过程水量平衡可知出库洪量等于入库洪量与库容减少量之和，可得：[8]

(5)

(6)

代入式(1)可得：

(7)

同理，溃口平衡以后:

(8)

即

(9)

综上，溃口发展的全过程可概化为：

(10)

2.2迭代算法的验证

本文所描述溃坝流量计算过程具体算法流程图见图1。

图1　溃坝流量过程线计算流程

将此计算模型代入以下工程实例[3]当中计算，大洼水库溃坝时，一些实测数据及数值模拟参数见表1、表2。

表1　溃坝实测数据

表2　大洼水库漫顶溃坝过程数值模拟参数表[3]

注H为坝高；W为坝顶宽度；S为下游坡比；B0为初始溃口宽度；Hco为初始溃口深度；Qc为上游入库流量；d50为平均粒径；d90/d30为粒径比；n为坝体孔隙率；γs为坝体颗粒重度；φ为坝体内摩擦角；θ为坝体下游坡角；c为坝体黏聚力，m为流量系数。

通过此数学模型编制的程序对上述工程实例进行计算可得:

t1=721.305s,z1=6.81478m,H1=9.7m,Qp=54.304m3/s,H2=7.958m,t2=2863.1s。根据计算数据得出的溃口流量过程曲线见图2。

图2　溃口流量过程线

计算流量过程与模型实测结果在规律上较为一致，计算溃口峰值流量Qp=54.304m3/s。略大于实测峰值流量Q=42.25m3/s,计算峰值流量出现在721s,而实测峰值出线在800s左右，数据较为接近，当溃口结束时计算时间约为47min,实测数据中溃口结束发展的时间为45min，具有较小误差。计算溃口流量过程线中右侧趋于定值是因为原模型假设中溃口最终状态是进出水量达平衡状态，曲线最终趋于定值，而实测溃口数据为停止进水，故实测流量过程线中曲线最终Q为零。模型计算图像的整体趋势与实测数据相似，故可说明模型在实际工程计算中是可用的，且具有较高准确度。

3　结　语

本文对溃口及洪水水流进行假设，以数学模型为基础编制程序对土石坝的溃口洪水流量进行了模拟计算，并对模型模拟计算的结果进一步进行计算分析，发现影响溃口流量及峰值出现时间的两个重要因素为溃坝的来水流量及土石坝坝体下游坡角。这两个因素分别从坝体外部洪水的影响和坝体自身两个方面描述出了土石坝漫坝溃坝的重要原因，同时提醒我们在进行土石坝的溃坝分析时要对洪水、土石坝自身材料、结构进行着重分析。

该模型及程序可以较好地运用到梯级水库防洪应急调度及风险分析当中，通过两个模型对同一工程实例的模拟计算分析，说明程序具有较高准确度。

综合对模型计算时的调试过程，土石坝的漫顶溃坝受到外来洪水及土石坝坝体自身的影响，也对土石坝在设计及建造过程提出了建议。在土石坝的设计建造过程中应该充分分析水文条件的影响，并对土石坝设计、施工的质量提出更高的要求。同时需要对溃坝模拟分析进行更深层次研究，以便可以更准确、更形象地描述土石坝漫坝时溃口的发展过程，并能更好地对梯级水库群溃坝风险分析做出贡献。

[1]水利部大坝安全管理中心.全国水库垮坝登记册[Z].南京：水利部大坝安全管理中心，2008.

[2]姚志坚，彭瑜.溃坝洪水数值模拟及其应用[M].北京：中国水利水电出版社，2013.

[3]陈生水.土石坝溃决机理与溃坝过程模拟[M].北京：中国水利水电出版社，2012.

[4]钱宁，万兆惠.泥沙动力学[M].北京：科学出版社，1999.

[5]韩其为，何明民.泥沙起动规律及起动流速[M].北京：科学出版社，1999.

[6]SINGH V P.Dam breach modelling technology[M].Dordrecht:Kluwer Academic Publishers，1996.

[7]李家星，赵振兴.水力学[M].南京：河海大学出版社，2001.

[8]邓刚.土石坝漫顶溃口洪水过程概化计算模型[A].中国大坝协会.高坝建设与运行管理的技术进展——中国大坝协会2014学术年会论文集[C].北京：中国大坝协会，2014.

Simulation analysis and calculation of earth-rock dam overtopping failure

LI Qinzhi

(XinjiangShiheziXinjiangManasiRiverBasinAdministration,Shihezi832000,China)

In the paper, dam failure mode of earth-rock dam is introduced briefly. Computing procedure is formulated aiming at the generalization mathematical model of earth-rock dam overtopping failure simulation analysis. In addition, the engineering example of Dawa Reservoir dam failure is combined for numerical simulation. The data is comparatively analyzed with measured data in the engineering example. The importance of mathematical models and assumptions on calculation results, precision and risk analysis in the process of earth-rock dam overtopping calculation is further described.

earth-rock dam; overtopping; model; calculation and analysis

10.16616/j.cnki.11- 4446/TV.2016.09.009

TV641

B

1005-4774(2016)09- 0033- 03