转子系统不平衡响应的逆向分析
2016-10-12刘翠红王克明
刘翠红,王克明,夏 锟,石 峰
(沈阳航空航天大学 航空航天工程学部(院),沈阳 110136)
转子系统不平衡响应的逆向分析
刘翠红,王克明,夏锟,石峰
(沈阳航空航天大学 航空航天工程学部(院),沈阳 110136)
不平衡引起的振动故障在航空发动机故障中最为常见,对不平衡响应进行计算分析在实际工程应用中具有重要意义。根据转子在单盘激励和多盘激励下的不平衡响应分析方法,提出了一种常见不平衡响应分析的逆向分析方法——位移激励法,即通过控制单盘或多盘的响应位移分析不平衡的方法。对比分析转子在不平衡激励下各盘的响应幅值和将不平衡盘的响应幅值作为位移激励时各盘的响应,结果表明2种方法同转频时各盘响应一致。为了避免转子挠度过大而发生碰摩,根据转子不平衡响应与各盘上不平衡量的分布关系,利用控制转子各盘响应位移的方法分析转子的不平衡响应,得到转子系统在某个转速下工作时各盘允许的最大不平衡量。
转子动力特性;不平衡响应;控制位移法;反共振;逆向分析
转子系统是旋转机械的重要组件,机械加工误差及装配误差,都将引起转子的不平衡。统计资料表明,旋转机械的故障约有60%源于不平衡引起的振动[1-2]。转子的不平衡响应是转子动力学研究的一个重要问题。目前对转子不平衡响应的研究大都是针对定转速时的稳态响应和变转速时的瞬态响应特性分析[2],主要应用2类方法:传递矩阵法和有限元法。传递矩阵法程序简单,计算机时较短,但是该方法比较适用于链式结构,对于大型复杂结构的转子动力学问题计算的精度不高;有限元法分析转子动力学问题考虑了转动惯量、陀螺力矩及剪切变形等影响因素,在计算不平衡响应及稳定性等方面的问题取得了很好的结果。
以往不平衡响应的计算大都是在不平衡激振力下计算转子各截面的幅频响应,本文则通过限制转子模型各盘的响应幅值[3-4],反求各盘上的不平衡量,即以控制位移的方法限制响应幅值求解不平衡量。已知响应求激励是振动力学中的逆问题。通过分析转子系统在限制了各盘响应幅值后的响应,得到不平衡分布,可以优化转子系统设计,大大减小由于转子挠度过大引起的碰摩故障,提高转子系统的安全性[5]。
1 理论基础
转子系统的动力学方程如式(1)所示。
(1)

不平衡量等于不平衡质量m和其质心距转子轴线的距离e的乘积如式(2)
U=me
(2)
不平衡产生的激振力如式(3)
F0=Uω2=meω2
(3)
2 有限元模型的建立
参照涡轮发动机的结构特征,利用ANSYS建立一个具有航空发动机转子基本特征的转子盘轴结构三维有限元模型[7-8],轴长L=1.5m,轴半径为0.02m,各盘的厚度均为0.04m,半径为0.2m,材料的弹性模量为2.1×1 011Pa,密度为7 850kg/m3。各轮盘分布如图1(a)所示,支承方案为两端简支。利用ANSYS有限元前处理功能划分网格,共划分11 810个单元,节点数为14 369,其中4个盘的盘心节点号分别为4 744,4 768,4 792和4 850,模型如图1(b)所示。有限元模型中转子为实体单元[9],单元类型选择三维八节点的Solid185,每个节点有3个自由度,轴承选择Combin214弹簧阻尼单元,刚度为3×107N/m。

图1 转子有限元模型
3 转子的固有特性计算
为了更好地分析转子不平衡响应,先对转子模型进行模态分析[10],计算前三阶固有频率和主振型以及前三阶临界转速。
利用ANSYS中QR阻尼法计算并提取转子前三阶固有频率,它们分别为10.628Hz、42.145Hz和77.140Hz,图2~图4为前三阶模态振型。
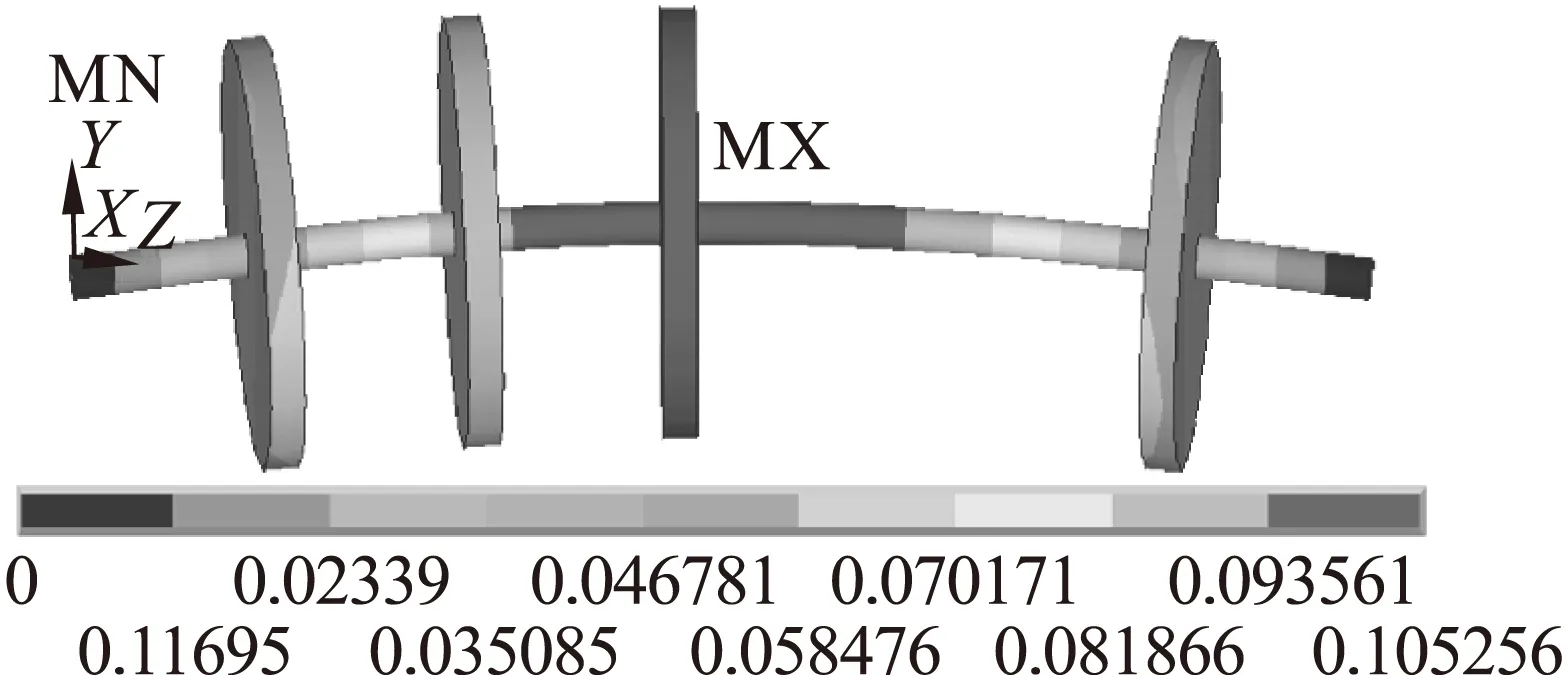
图2 第一阶模态振型

图3 第二阶模态振型

图4 第三阶模态振型
通过计算转子各转速下的模态,画出Campbell图,如图5所示。从图5中可以得到转子系统前三阶临界转速[11-12]分别为660.813r/min、2 917.702r/min和5 321.09r/min及对应频率11.014Hz、48.628Hz和88.685Hz。由于模型中转子转动时会产生陀螺效应,陀螺力矩使转子不易弯曲,所以前三阶临界转速对应的频率比前三阶固有频率高。
4 转子不平衡响应分析
4.1单盘激励下的不平衡响应
假设在盘上有一不平衡量U=me=10g·cm,等效成不平衡激振力F0=Uω2。由于ANSYS计算中每一步自动载入ω2,所以在1号盘心位置(4 744号节点)处施加旋转载荷0.000 1 ω2。应用谐响应分析法分析不平衡响应[13-15],设置谐响应分析频率范围0~100Hz,分析子步数为100,对转子系统0~100r/min转频范围内进行谐响应分析。图6(a)~图6(d)分别为各盘Y方向的幅频响应曲线(X方向与Y方向除相位外,其他响应情况一致),图6中显示各节点均在11Hz、49Hz和88Hz处出现峰值,这是由于在不平衡激振力下,转子系统在临界转速处发生共振,距离共振转速越远,响应幅值越小。

图5 坎贝尔图

图6 盘心幅频响应曲线
表1为4个盘的盘心节点在不同转速下的响应位移,转频为10Hz。比较各盘心节点处的响应,2号盘和3号盘响应明显比1号盘和4号盘的响应幅值大,这是因为这一转速靠近第一阶临界转速,振型接近一阶模态振型,2号盘和3号盘比1号盘和4号盘的盘心节点更靠近转子中心,所以响应幅值较大。另外,查看各节点在每步转速下的响应幅值时还发现在25Hz和65Hz这两个转频时响应幅值比其他转频下的幅值普遍小几个数量级。
对于相同的转子模型,已知1号盘上有10g·cm的不平衡量,转频为10Hz时1号盘的响应幅值为1.255 9μm,控制1号盘心节点的位移X=1.255 9μm,Y=-1.255 9μm。设置谐响应分析频率范围0~100Hz,分析子步数为100,对转子系统进行谐响应分析。分析限制1号盘响应幅值时其余盘的幅频响应曲线。以3号盘心节点为例画出Y方向的幅频响应曲线如图7。图中25Hz和65Hz为反共振频率,所以出现峰值。从图7(b)中可以看到转频为10Hz时3号盘心的振动幅值为2.57μm与不平衡力引起的响应幅值相等。

表1 各盘心节点在力激励下的响应

图7 3号盘心幅频响应曲线
计算各盘心节点在3个转频下的响应幅值,结果见表2。对比表2与表1可以看出,控制1号盘心位移,转频为10Hz时,转子其他各盘心响应幅值与不平衡激振力下的响应幅值相同。
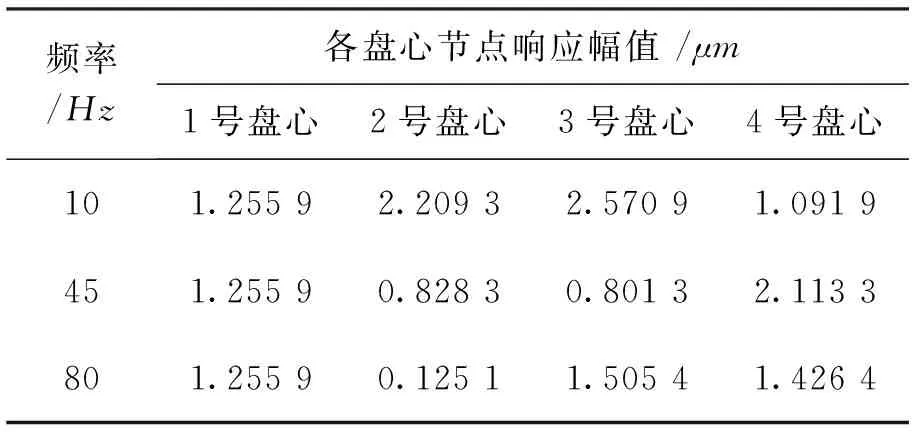
表2 限制1号盘心位移时各盘的响应
从表2中可看出,同频率时,单盘不平衡力激励下的响应与控制位移时其他各盘的响应一致。
4.2双盘不平衡激励下的响应
对该转子模型,若3号盘上不平衡量为5g·cm,4号盘上不平衡量为10g·cm,计算系统不平衡响应。4个盘的盘心节点处幅频响应曲线如图8(a)~图8(d)所示。
表3(a)和表3(b)分别给出了两盘偏心同向与偏心反向时的各盘心节点的响应幅值。
由表3可以看出,在转频为10Hz时,2号盘心节点和3号盘盘心节点位置的响应幅值较大,这是由于这一转速非常靠近第一阶临界转速,振型接近第一阶模态振型。通过计算各转速下转子的响应还发现转子各截面在54Hz转频下响应幅值比其他转频下要小几个数量级,这一转频为反共振频率。与同向不平衡力下的响应幅值相比,反向不平衡力下的不平衡响应在前两阶临界转速附近振动幅值都减小,第三阶临界转速附近振动峰值增大,这与高阶振型耦合有关。

图8 盘心幅频响应曲线
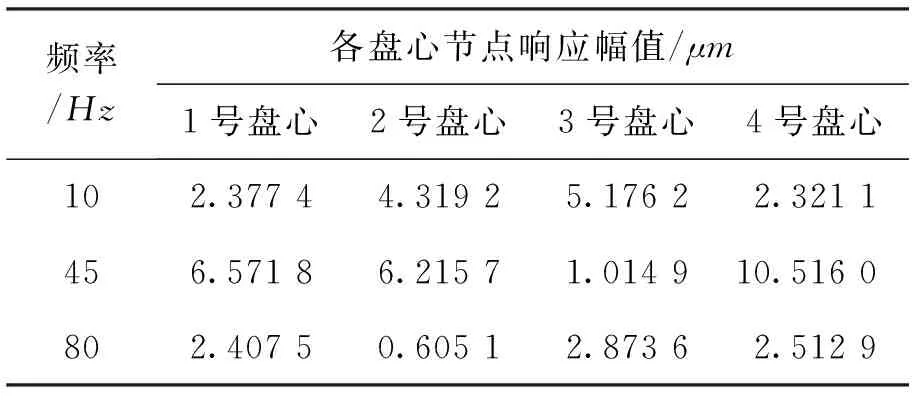
表3(a) 各盘心节点在偏心同向时的响应
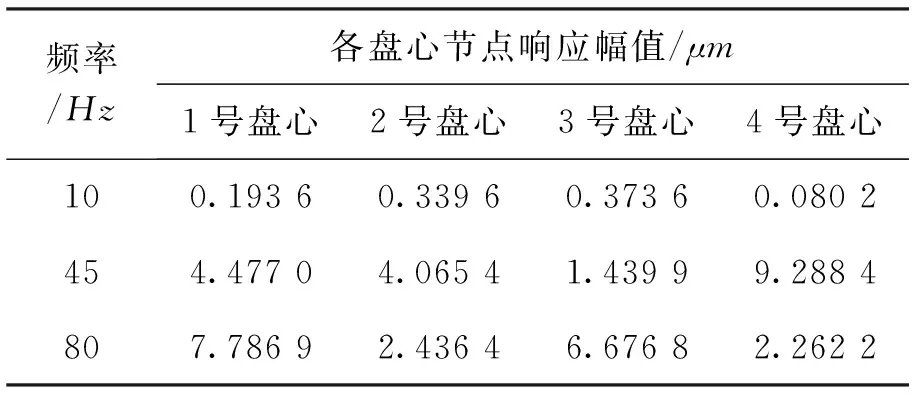
表3(b) 各盘心节点在偏心反向时的响应
3号盘与4号盘上不平衡量产生的激振力同向时,控制转子这两个盘的响应位移分别为10Hz转速下的响应幅值5.176 2μm和2.321 1μm,计算同时控制转子两个盘的响应幅值时各盘的不平衡响应,与控制一个盘的响应幅值时的不平衡响应分析方法相同。图9为控制转子3号盘和4号盘的位移时,1号盘心节点Y方向的幅频响应曲线。幅频响应曲线中会在反共振频率54Hz附近出现峰值。
表4给出了各盘盘心节点分别在三个转速下的响应幅值。表3与表4相对比可以看出,转子在转频为10Hz时各盘的响应与转子在两同向不平衡激振力下的响应幅值相同。这说明同频率下,控制位移时的响应与不平衡激振力下其他各盘的响应幅值一致。
4.3控制响应幅值求最大允许不平衡量
由4.1中已知1号盘上有幅值为0.000 1ω2的不平衡激振力,转频为10Hz时,Y方向上最大响应位移为1.255 9μm。计算此转速下控制1号盘的响应幅值不超过10μm,盘上允许的最大不平衡量U由
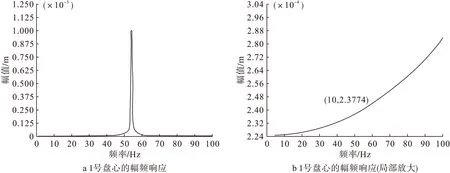
图9 1号盘心的幅频响应
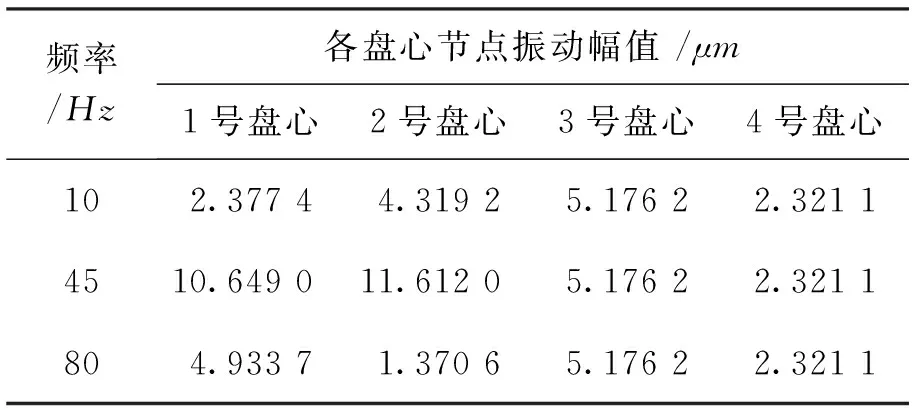
频率/Hz各盘心节点振动幅值/μm1号盘心2号盘心3号盘心4号盘心102.37744.31925.17622.32114510.649011.61205.17622.3211804.93371.37065.17622.3211
算得U=7.962 4×10-4kg·m。因此,若转频为10Hz要求盘的最大响应位移为10μm时,盘上允许的不平衡量不能超过79.624g·cm。
1号盘上有79.624g·cm的不平衡量时,利用ANSYS有限元软件计算该盘的最大响应位移。通过计算得到1号盘心节点Y方向的幅频响应曲线如图10所示:

图10 1号盘心的幅频响应
在转频为10Hz时,Y方向的响应幅值为9.999 99×10-6m,约10μm,与理论计算的结果一致。这说明仅第一级盘上有不平衡量时,若要限制第一级盘在Y方向上的最大响应位移不超过10μm,控制盘上所有不平衡量在此方向上的矢量和不超过79.624g·cm即可达到要求。
实际转子系统的每个盘上都有或多或少的不平衡量。这种情况下应先计算每个盘上的不平衡量对转子不平衡的影响,以转子工作转频为20Hz时为例,表5中给出了1kg·m的不平衡量分别分布在不同盘上时(同方向)各盘的响应位移。
各盘的响应是各盘不平衡影响的叠加,根据表5可以列出在不同的不平衡量分布情况下各盘的响应方程组,如式(4)所示
(4)
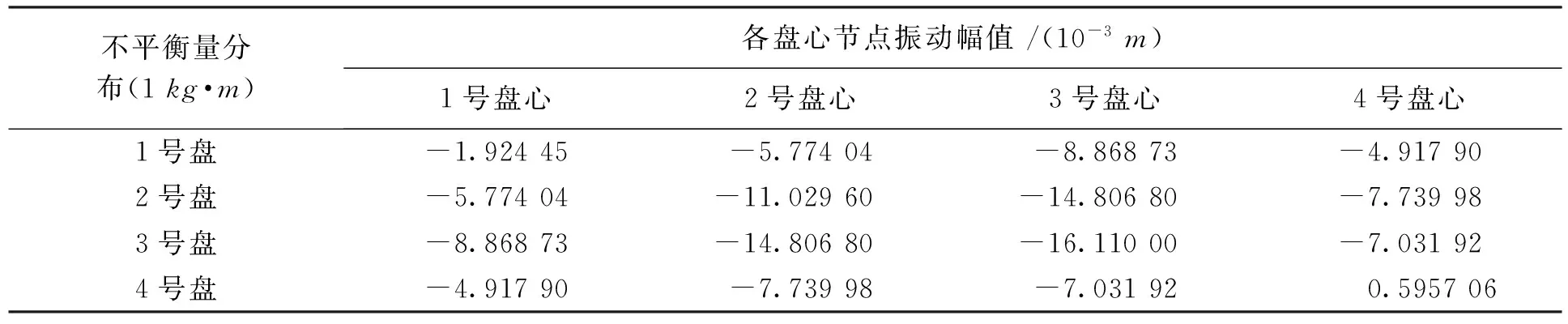
表5 不同的不平衡量分布下各盘响应位移
注:负号(-)表示节点的振动方向为不平衡合力矢量的反方向。
提取系数矩阵
D=-10-3×

定义列向量U
U=[U1U2U3U4]T
(5)
其中,U1、U2、U3和U4分别为4个盘上的不平衡量,此时4个盘的响应位移X1、X2、X3和X4通过公式(6)可以求出
X=[X1X2X3X4]T=DU
(6)

其中,D-1为D的逆矩阵。将计算求得的不平衡量分别添加在4个盘上,利用ANSYS软件分析不平衡响应,各盘在转频为20Hz时的响应幅值如表6所示。

表6 各盘响应幅值
由表6可看出,将求解的4个盘的不平衡量分别加在盘上,各盘的响应位移不超过规定的最大振动幅值,其响应幅值与限定的振动幅值基本一致,其中的微小误差来源于响应系数矩阵与不平衡量的取位精度。这说明控制各盘响应幅值计算得出的各盘上允许的最大不平衡量是正确的。
5 结论
文中利用控制位移求响应的方法(位移激励法),根据最大允许的响应位移反求出不平衡量的范围,这对实际转子的设计及制造有一定的参考价值。具体结论如下:
(1)对比分析同转频时不平衡力激励和位移激励的响应情况,结果表明各盘的响应幅值是一致的,验证了控制位移求响应这种方法是可行的;
(2)不平衡激励下各盘的幅频响应曲线在临界转速处出现峰值。位移激励下施加激励的盘的幅频响应为一条水平直线,其他各盘的响应曲线在临界转速不会出现峰值,而是在不平衡盘的反共振频率对应的转速处出现峰值;
(3)不平衡激励可以求出转子各盘的响应,而控制位移反求不平衡量的方法只能求出控制位移的盘上的不平衡量。这是由于此方法限定一个盘的响应位移时,计算过程中认为此位移是由该盘上不平衡量引起的,其他盘均不存在不平衡;
(4)多盘不平衡响应是每个不平衡盘分别引起的响应的叠加。若要控制转子n个盘的响应位移就可以列出相应的n元方程组,求出对应的n个盘上的不平衡量。
[1]陈予恕,张华彪.航空发动机整机动力学研究进展与展望[J].航空动力学报,2011,32(8):1371-1391.
[2]孟光.转子动力学研究的回顾与展望[J].振动工程学报,2002,15(1):1-9.
[3]HUANGXCH,LIUXT,HUAHX.Effectsofstiffnessandloadimperfectionontheisolationperformanceofahigh-static-low-dynamic-stiffnessnon-linearisolatorunderbasedisplacementexcitation[J].InternationalJournalofNon-LinearMechanics,2014(65):32-43.
[4]HANGANG,CHENYUSHU.Principalresonancebifurcationofbending-torsioncouplingofaero-enginecompressorbladewithassembledclearanceunderlateraldisplacementexcitationofrotorshaft[J].NonlinearDynamics,2014,78(3):2049-2058.
[5]李聪,常颖,张风波.基于ANSYS的转子系统不平衡响应分析[J].测控技术,2011,30(12):116-118.
[6]瓮雷,杨自春,曹跃云.转子系统临界转速计算及不平衡响应分析[J].四川兵工学报,2013,33(11):65-69.
[7]王军锋,孙康.基于有限元法的转子临界转速计算[J].机械设计,2012,29(012):10-13.
[8]赵文涛,陈果,李琼,等.航空发动机机匣支承动刚度有限元计算及验证[J].航空计算技术,2011,5:34-38.
[9]陈萌,马艳红,刘书国,等.航空发动机整机有限元模型转子动力学分析[J].北京航空航天大学学报,2007,33(9):1013-1016.
[10]杨康,韩涛.ANSYS在模态分析中的应用[J].佳木斯大学学报(自然科学版),2005,23(1):81-84.
[11]缪辉,王克明,艾书民,等.双转子系统临界转速的有限元分析[J].沈阳航空航天大学学报,2011,28(5):27-31.
[12]WANGJQ,WANGF,ZONGM.Criticalspeedcalculationofmagneticbearing-rotorsystemforahighspeedmachine[C].ProceedingsoftheChineseSocietyofElectricalEngineering,2007,27(27):94-98.
[13]姚学诗,周传荣.基于预应力法的转子不平衡响应研究[J].振动与冲击,2005,24(2):84-86.
[14]BONELLOP,HAIPM.Computationalstudiesoftheunbalanceresponseofawholeaero-enginemodelwithsqueeze-filmbearings[J].JournalofEngineeringforGasTurbinesandPower,2010,132(3):032504.
[15]孙红岩.利用有限元进行转子系统的动力学分析[D].西安:西安建筑科技大学,2008.
(责任编辑:宋丽萍英文审校:赵欢)
Reverseanalysisofrotorunbalanceresponse
LIUCui-hong,WANGKe-ming,XIAKun,SHIFeng
(FacultyofAerospaceEngineering,ShenyangAerospaceUniversity,Shenyang110136,China)
Vibrationfaultcausedbyunbalanceisthemostcommonfaultforaero-engine,andthecalculationandanalysisofunbalanceresponseissignificantforthepracticalengineeringapplication.Accordingtotheanalysismethodofrotorunbalanceresponseexcitedbyonediscandmorediscs,areversemethodofthecommonunbalanceresponseanalysis,i.e.displacementexcitationmethodwasproposed.Thismethodanalyzesrotorunbalancebycontrollingonediscormorediscsresponsedisplacement.Theresponsedisplacementsofthediscsexcitedbyunbalanceandtheresponseofthediscsexcitedbytheresponsedisplacementsofunbalancediscswerecomparedandanalyzed.Theresultsshowthattheresponsedisplacementofeachdiscisidenticalforthetwotypesofexcitationatthesamerotatingspeed.Inordertopreventtherubbingcausedbyoverlargedeflectionofrotor,themaximumallowableunbalanceisobtainedbythedisplacementrestrictionmethodaccordingtotheunbalanceresponsesofrotorandunbalancedistributionofthediscs.
rotordynamiccharacteristic;unbalanceresponse;displacementrestrictionmethod;anti-resonance;reverseanalysis
2015-11-18
刘翠红(1990-),女,山东荷泽人,硕士研究生,主要研究方向:航空发动机强度、振动及噪声,E-mail:565582372@qq.com;王克明(1954-),男,辽宁沈阳人,教授,主要研究方向:航空发动机强度、振动及噪声,E-mail:wmk308@126.com。
2095-1248(2016)04-0030-08
V231.92
A
10.3969/j.issn.2095-1248.2016.04.006
