民用飞机球面框的优化和方案设计
2016-10-12李旭,晨曦,孟超
李 旭,晨 曦,孟 超
(1.中航沈飞民用飞机有限责任公司 工程研发中心,沈阳 110179; 2.沈阳航空航天大学 理学院,沈阳 110136)
民用飞机球面框的优化和方案设计
李旭1,晨曦1,孟超2
(1.中航沈飞民用飞机有限责任公司 工程研发中心,沈阳 110179; 2.沈阳航空航天大学 理学院,沈阳 110136)
机身球面框是民用飞机机身增压舱的端框,是飞机的主要结构部件。球面框复杂的结构形式和装配要求,极大地增加了设计难度。在某型号飞机的概念设计阶段,基于先进的OptiStruct优化技术,对球面框初始构型进行了拓扑优化。参照优化后的密度云图,调整经向加筋的结构位置,给出3种满足强度要求和刚度要求的初始设计方案。使用MSC.Patran建立细节有限元模型模拟3种方案,计算每个球面框方案在增压载荷工况下的应力分布,为后续详细结构设计提供数据支持。
民用飞机;球面框;优化;有限元;应力
在民用飞机机体结构中,球面框位于前、后机身,是机身增压舱的端框,主要承受机身客舱内的增压载荷。大曲率的半球形壳体通过薄膜应力来承担压力载荷,比平面框结构效率高。但由于球面框位于前、后机身收缩段,复杂的机体结构外轮廓面使球面框为多曲率的曲面,同时球面框的设计还需要考虑装配、制造和维护要求,这些都增加了球面框的设计难度。目前国内外学者对球面结构的研究取得了巨大进展,获得了很多优秀成果[1-6]。
专业强度分析软件和优化软件的不断开发和使用,弥补了理论分析在工程项目中难以简单应用的不足。在现代飞机结构概念设计阶段,设计人员除了依靠工程经验确定结构部件的初始结构形式外,越来越趋向于将复杂的结构实现模型化[7-10],在初始细节模型基础上进行静强度分析和优化设计,对结构尺寸进行优化调整,使结构分布更加合理。Altair OptiStruct是以有限元法为基础的结构优化设计工具,提供拓扑优化、形貌优化、尺寸优化、形状优化以及自由尺寸和自由形状优化技术[11-12]。在概念设计阶段可以对产品总体构型进行优化;在详细设计阶段可以对产品尺寸和形状进行优化,帮助设计工程师找到更好的设计方案。本文应用OptiStruct优化技术对球面框进行拓扑优化分析,依靠工程经验和分析结果,调整结构布局,给出3种满足强度要求和刚度要求的球面框概念设计方案,支持后续的结构详细设计工作。详细设计阶段球面框的强度分析可参考文献[13]和[14]。
1 结构和载荷
球面框是机身增压舱的端框,将机身气密区与非气密区分开,承受客舱内的增压载荷并将其承受的载荷通过连接传递给机身。球面框由环框、球皮、经向加筋、顶盖以及破损安全环形带板等结构组成,如图1所示。

图1 球面框结构示意图
在结构概念设计阶段,外载荷输入数据不全,球面框的设计载荷为纯气密增压载荷。参考文献[15]给出局部球皮单元应力水平为:
(1)
式中σ1为经向膜应力;σ2为环向膜应力;q为气密增压载荷;R为球皮单元局部曲率半径;t为单元厚度。
2 结构设计
2.1优化方法
优化设计有三要素:设计变量、目标函数和约束条件。优化的过程就是寻求理想的设计变量值,在满足约束条件情况下,实现最优的设计目标。优化设计的数学模型可以用目标函数表示为
f(X)=f(x1,x2,…,xn)
(2)
优化设计的约束条件为
gj(X)≤0j=1,2,…,m
(3)
(4)

文献[5]、[6]给出球面结构优化分析方法,关于更多的OptiStruct优化理论和有限元分析方法参考文献[11]、[12]。
2.2优化分析
根据后机身曲面尺寸、装配、制造等要求,确定球面框的球面构型,多曲度球皮结构如图2所示。在球面构型基础上,使用OptiStruct拓扑优化分析,规划球面框经向加筋位置,其中球皮材料2024-T42,规范AMS-QQ-A-250/5。为了确保结构具有足够刚度,定义球皮单元初始厚度8 mm。
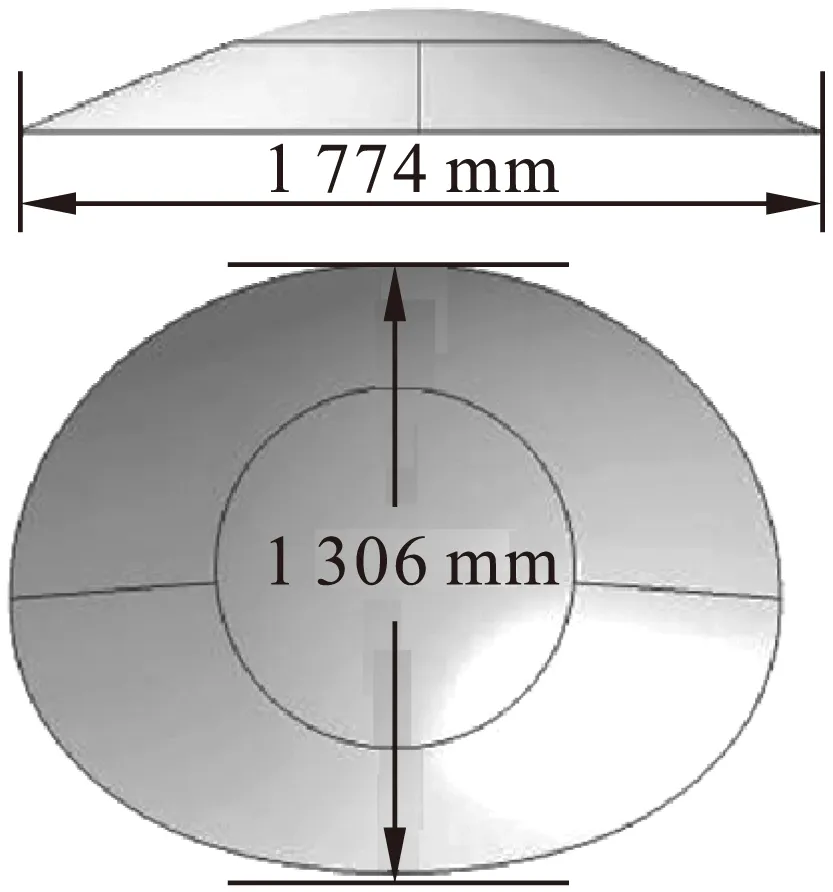
图2 球皮结构
基于优化设计的数学模型,定义优化目标是体积最小化,约束条件是球面框的最大位移不超过设计值,设计变量为单元密度。在球面框的概念设计优化分析中,考虑纯气密增压载荷0.082 8 MPa正压条件下,最大位移不超过6 mm的球面框的优化分析和后续的静强度分析。细节有限元模型的分析区域为球面框的内部结构区域,定义边界条件是限制球框边缘节点的6个方向自由度。
通过对比球面框上球皮多个位置的曲率半径,可知球皮左右两侧区域局部半径较大,球皮单元应力会大于其他位置。图3给出使用OptiStruct进行拓扑优化5次迭代后的密度云图,显示迭代计算后的密度调整情况,低密度区的结构厚度可以进一步减小。通过优化分析的密度云图,可以得到具体需要加强的位置和可减少厚度的位置,有利于结构设计和产品减重。
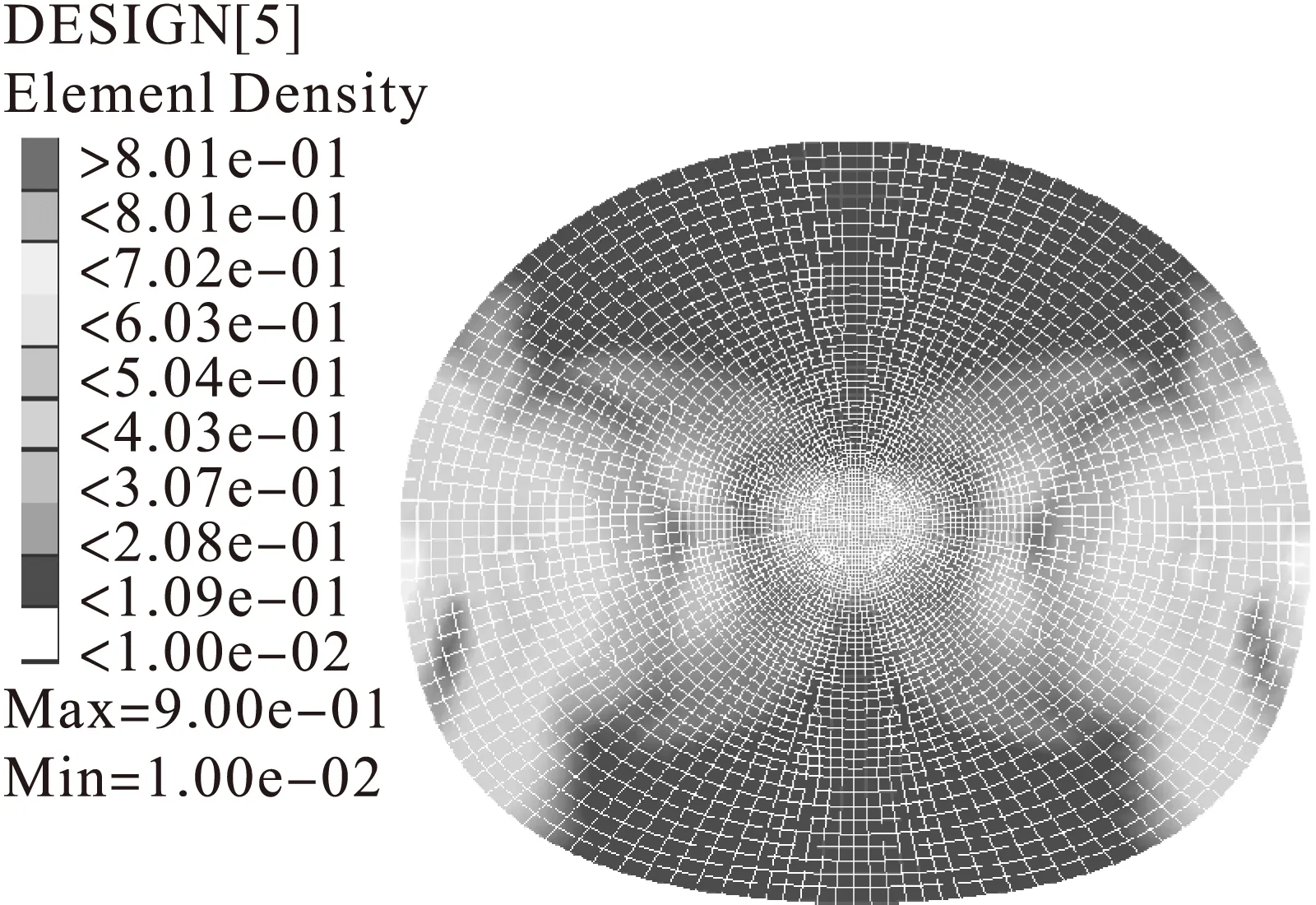
图3 密度云图
2.3方案设计与分析
经向加筋是球面框的主要结构单元,对球面框起到经向加强支持作用,提高球皮的稳定性和抑制球皮裂纹扩展。在概念设计阶段,结合工程经验和优化分析结果,给出3种经向加筋结构布置方案,对比3种方案的应力水平分布,为后续结构设计提供数据支持。
方案一,经向加筋的分布方式为12根加筋均匀分布,如图4所示。通过静强度分析得到球面框分析区域内的应力水平分布,如图5所示。最大应力位置在水平加筋下侧,应力值为129 MPa,满足静强度设计要求。
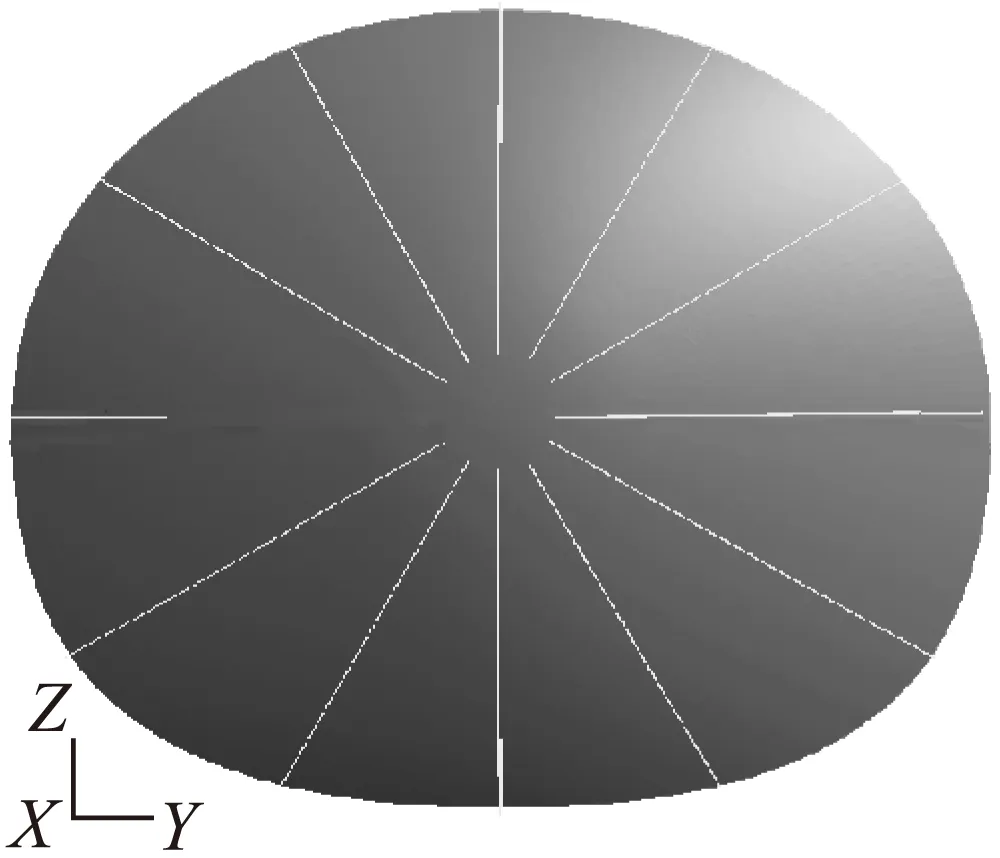
图4 典型加筋位置
方案二,结合优化分析的密度云图,在方案一的基础上,使球面框左右两侧水平加筋向下偏移5°,将水平加筋布置在高密度区域,提高筋条结构效率,结构形式如图6所示。通过静强度分析得到球面框分析区域内的应力水平分布,如图7所示。最大应力位置在水平加筋下侧,应力值为120 MPa,满足静强度设计要求。

图5 应力云图
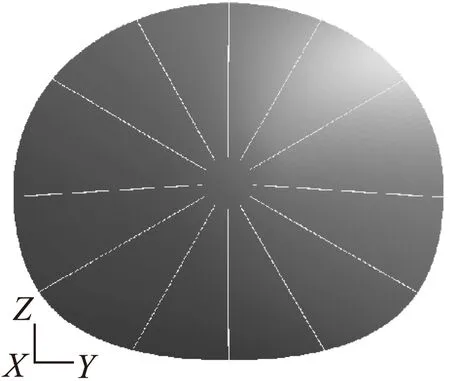
图6 方案二的加筋位置

图7 方案二的应力云图
方案三,根据优化分析的密度云图,整体调整经向加筋的位置,在高密度区域充分展现加筋的结构效率。首先将左右3号、4号加筋布置在图3的高密度区域,3号加筋由图4中的水平加筋位置向上旋转18°,4号加筋由水平加筋位置向下旋转16°,其他加筋均布在球皮结构上,如图8所示。通过静强度分析得到球面框分析区域内的应力水平分布,如图9所示。球面框最大应力位置发生在优化分析中的高密度区域,最大应力值为108 MPa,满足静强度设计要求。

图8 优化的加筋位置

图9 方案三的应力云图
3 结论
结合工程经验和优化分析结果,共给出了3种经向加筋结构布置方案。通过细节有限元模型模拟计算可知3种方案基本满足静强度设计要求。
从工程制造装配来看,方案一便于经向加筋在球皮上的定位和连接,很多机型的球面框都采用均匀对称布置经向加筋。在方案三中,每个加筋都具有一定角度,加筋的位置相对其他两个方案较难定位,增加了工装设计和装配难度,提高了制造成本。
从强度分析角度看,对比3个方案应力水平,方案三的应力水平分布更均匀,应力值更小。基于拓扑优化结果调整经向加筋布置,可以使球面框应力水平分布相对均匀,有效地增强了球面框的强度和稳定性,提高了筋条的结构效率。
球面框是机身气密舱的主要结构,球面框结构单元应力水平的分布除了与结构尺寸,如曲率半径、厚度有关,还与球皮上的系统开口、球面框与机身地板的连接等有关。在飞机项目概念设计阶段,基于总体理论构型,可以先根据工程经验和先进的强度分析软件,如MSC.Patran,Altair HyperWorks等给出一种或几种初始结构方案。随着项目研制工作的推进,再根据详细的系统安装、装配、制造等结构设计要求和强度设计要求,选取相对合适的结构方案。如果偏重考虑装配和工艺性,可选取方案一的垂直、水平加筋布置,这种布置易于工装定位;如果偏重考虑系统安装和强度设计要求,可选取方案三协调布置加筋位置,可以优化结构,减轻重量。
[1]BLACHUT J.Pressure vessel components:some recent developments in strength and buckling[J].Progress in Structural Engineering and Materials,1998,1(4):415-436.
[2]BLACHUT J.Buckling of multilayered metal domes[J].Thin-Walled Structures,2009,47:1429-1438.
[3]CAO Z G,FAN F,SHEN S J.Elasto-plastic stability of single-layer reticulated domes[J].China Civil Engineering Journal,2006,39(10):6-10.
[4]FAN F,YAN J C,CAO Z G.Elasto-plastic stability of single-layer reticulated domes with initial curvature of members[J].Thin-Walled Structures,2012,60:239-246.
[5]TENG T L,YU C M,WU Y Y.Optimal design of filament- wound composite pressure vessels[J].Mechanics of Composite Materials,2005,41(4):333-340.[6]SHALLAN O,ERAKY A.Optimum design of space tensegrity dome[J].International Journal of Engineering and Innovative Technology,2014,3(9):47-54.
[7]RIBERT J M.Structural engineering analysis by finite element[M].New Jersey:Prentice Hall,1990.
[8]EUGENIO O.Structural analysis with the finite element method[M].Springer,2013.
[9]SURANAK S,REDDY J N.The finite element method for boundary value problems:mathematics and computaion[M].CRC press,2016.
[10]朱菊芬.非线性有限元及其在飞机结构设计中的应用[M].上海:上海交通大学出版社,2011.
[11]张胜兰,郑冬黎,等.基于HyperWorks的结构优化设计技术[M].北京:机械工业出版社,2007.
[12]李楚琳,张胜兰,等.HyperWorks分析应用实例[M].北京:机械工业出版社,2008.
[13]赵俊辉,孙为民,童明波.气密载荷下机身球面框的强度分析[J].飞机设计,2009,29(2):21-24.
[14]刘昌沅,郭伟毅,等.气密座舱球面框的非线性有限元结构设计[J].航空精密制造技术,2004,40(5):22-25.
[15]牛春匀.实用飞机结构应力分析及尺寸设计[M].北京:航空工业出版社,2009.
(责任编辑:吴萍英文审校:赵欢)
Optimization and design of spherical frame at civil aircraft
LI Xu1,CHEN Xi1,MENG Chao2
(1.Research and Development Center,AVIC SAC Commercial Aircraft Company Ltd.,Shenyang 110179,China;2.College of Science,Shenyang Aerospace University,Shenyang 110136,China)
The spherical frame is the bulkhead of pressure cabin at civil aircraft,which is a major part of fuselage structure.The complicated configuration and assembly requirement of spherical frame remarkably increase the difficulty in design.The initial configuration of spherical frame was topologically optimized based on the advanced OptiStruct technique in the initial stage of structural concept design.According to the density plots,the structural locations of meridian stiffeners were adjusted,and three initial project designs were proposed to meet the requirements about strength and rigidity.Detailed finite element model was built to simulate the spherical frame of fuselage using MSC.Patran through the three designs,and the stress distribution under the pressurized load was respectively calculated for the designs,which provides the data support for detailed structure design in the future.
civil aircraft;spherical frame;optimization;finite element;stress
2015-12-15
李旭(1983-),女,辽宁锦州人,工程师,主要研究方向:飞机结构设计,E-mail:li.xu@sacc.com.cn。
民用航空与安全工程
2095-1248(2016)04-0085-04
V223
A
10.3969/j.issn.2095-1248.2016.04.015
