沙画图像特征的可计算美学分析*

吴　涛，杨俊杰，冉国洪

1.岭南师范学院 信息科学与技术学院，广东 湛江 524048 2.广东高校数字化学习工程技术开发中心，广东 湛江 524048 3.岭南师范学院 美术学系，广东 湛江 524048

沙画图像特征的可计算美学分析*

吴涛1+，杨俊杰2，冉国洪3

1.岭南师范学院 信息科学与技术学院，广东 湛江 524048 2.广东高校数字化学习工程技术开发中心，广东 湛江 524048 3.岭南师范学院 美术学系，广东 湛江 524048

WU Tao,YANG Junjie,RAN Guohong.Computational aesthetics analysis on sand painting style.Journal of Frontiers of Computer Science and Technology,2016,10(7)：1021-1034.

沙画是一种风靡全球的新视觉艺术形式，计算机沙画艺术方兴未艾。在可计算美学的研究框架下，引入了色彩模式、主题色、色相环、Benford度量、分形维、全局对比因子、Shannon熵、彩色度、数据场复杂度、Tamura纹理等量化特征维，对沙画艺术的创作风格进行了数值计算和统计，探索了静态沙画图像的可计算美学分析。实验结果表明，计算机辅助的客观美学评价能够一定程度上反映不同沙画作品创作风格上的异同点，基本符合人类主观审美认知，作为构建计算机沙画艺术与沙画表演作品之间的有益桥梁，可为沙画艺术创作风格的主观评价提供客观依据和量化补充，也为计算机沙画艺术自动创作提供参考和借鉴。

艺术风格；沙画艺术；可计算美学；图像统计；图像可视化

1　引言

沙画表演是近年来刚刚兴起并迅速风靡全球的一种新型视觉艺术表现形式，其特点是“以沙为墨，用指代笔”，这种风格源自于匈牙利的户外艺术家Ferenc Cako（http://ferenccako.com/）。艺术家在舞台灯箱照射的白色背景板上现场用手指控制细沙作画，根据一定的主题通过前期创作与构思，以类似连环画的形式传递信息或者讲述故事，并将沙子绘制和手指表演的全过程投影在屏幕上展示给观众。目前，沙画表演在各种公共活动的现场创意非常流行，充满个性的沙画表演也是婚礼、生日宴上众多时尚人士和爱好者的追求目标。其中利用照片素材现场创作合适的沙画图像并保证表演艺术的独创性是首要核心任务。该沙画表演依次包含前期静态图像创作结果和后期动态手势表演过程两个阶段。

在物质生活日益丰富，计算机技术迅猛发展的今天，利用计算机辅助沙画表演艺术的精神生活需求也越来越强烈，不妨简称为计算机沙画艺术，包括以定性和定量方法利用计算机辅助分析沙画表演艺术风格，构造具有创作灵感的智能环境，建立计算机辅助生成的计算模型和工具，开展交互或自动的沙画艺术创作，进而创造出若干独具一格的沙画表演作品。国内外研究者也敏锐地捕捉到计算机沙画的现实意义，已展开了若干阶段性的研究和开发[1-5]，并在不同层面上取得了一定的有益成果。

纵观与计算机沙画艺术有关的现有研究成果，主要体现了以下趋势。

（1）新：计算机沙画艺术研究新奇有趣，并逐步引起国内外相关领域研究者的重视，但值得注意的是，现有文献表明[1-5]，除Sand Draw汉化版之外，在国内（不含港澳台地区）鲜有其他有关的学术报道。

（2）少：沙画艺术兴起不久，计算机沙画研究的起步也相对较晚，相关学术成果并不多见，甚至很多只是类似于雾气屏幕的小软件开发，仅利用到计算机图形学领域很早期的成熟技术，尚未考虑更深层次的科学问题。

（3）偏：现有大多数研究更偏重于人机交互技术，以模拟介质为主，计算机主动参与的自动化程度不高。

抛开沙画的独特艺术形式，在可计算美学研究范畴，计算机辅助的艺术美学分析与创作已经取得了若干有意义的阶段性成果。在美学分析方面，Taylor等人利用分形法量化分析了Pollock的滴彩画作品[6]；Li等人提出了油画的若干美学客观评价依据[7]；Heijer探讨了艺术作品的视觉对称性和平衡性[8]；普园媛等人以信息论为理论基础，分析了中西方艺术家的绘画视觉艺术风格[9]。在美学创作方面，通过构建数学、物理模型并设计算法已能自动创作多种艺术风格，取得了若干重要成果，包括铅笔画、水彩画、油画、卡通画以及具有中国特色的水墨画、剪纸、烙画、乱针绣等[10-12]。

尽管如此，沙画作为一种独特的艺术形式，仍然具有其特殊性。静态沙画图像的创作是沙画表演艺术的重要前提，直接决定了后期动态手势的表演过程。不同的沙画师具有其独特的艺术创作风格，对这些沙画创作风格的统计与分析，有利于更客观地挖掘国内外沙画师的颜色使用、偏好习惯等，也有助于使计算机更好地模拟这些风格，并有望逐步实现自动创作。可计算美学是近年来计算机图形图像处理领域的新兴方向之一，通过若干评价指标定量分析和发现图像中所包含的定性美学价值[13-14]。有鉴于此，本文对国内外沙画艺术的创作风格进行量化统计，探索沙画图像的可计算美学分析。

2　沙画及其量化分析方案

2.1沙画概述

沙画作品按照形式可分为静态、动态、动画3种类型。其中，静态沙画是指不限制时间，精细绘制的单幅沙画作品。动态沙画是指在规定时间内完成一连串的主题画面表演。动画沙画是指所表演的视觉内容在预设的图形之间有关联性变化。沙画作品按照色彩可分为黑白、单色、彩色3种类型。其中黑白沙画的灯光背景为白色，标准黄沙在灯光照射下显示为黑色效果。单色沙画的灯光为单种颜色，任意颜色沙子在灯光下显示为单色效果。彩色沙画的灯光为变幻的彩色，任意颜色沙子在灯光下显示为彩色效果。

本文侧重于关注沙画师对作品最终呈现的创作风格，忽略表演过程，并不严格区分沙画的表现形式。因此，动态或动画沙画的呈现结果作为一幅完整的沙画图像，在本文的研究中与静态沙画并无本质区别。同时，分析沙画师的色彩喜好也是本文的重要研究内容之一。因此，本文在收集沙画样本时也不严格限定其色彩类型，黑白、单色、彩色沙画都是本文的研究范畴。

2.2静态沙画的量化分析方案

本文的量化分析方案依次包括4个步骤：

步骤1收集并整理沙画静态图像，包括互联网搜索辅以人工分拣，项目组购买或被赠予等方式，共667幅沙画图像。

步骤2分别提取这些图像在3种颜色模式下的特征向量，包括灰度模式、HSV模式、RGB模式，实施简单的统计。

步骤3依次提取Benford度量、分形维、全局对比因子、Shannon熵、彩色度、数据场复杂度、Tamura纹理等图像量化美学特征。

步骤4对不同图像的同类特征进行比较分析，挑选代表性图像实施主题色、色彩和谐模式分析等，总结并挖掘规律。

本文的量化分析方案如图1所示。

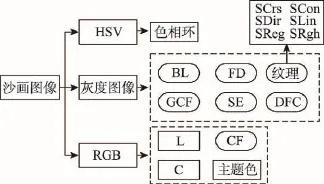
Fig.1　Schematic diagram of quantitative analysis图1　量化分析方案示意图

3　量化特征

可计算美学特征的评价指标众多[15]，本文计算了与图像直接相关的光强、光彩等若干基本统计特征，分析了代表性静态沙画图像的调色板风格，也统计了Benford度量、分形维、全局对比因子、Shannon熵、彩色度、Tamura纹理等5个美学度量，还包括本文提出的数据场复杂度度量。

3.1基本统计特征

沙画图像创作结果的最直观量化评价是均值、方差、最大值、最小值等若干基本统计特征，为充分量化沙画图像的特征，分别提取了RGB模式下的红(R)、绿(G)、蓝(B)3个颜色分量，HSV颜色模式下的色调(H)、饱和度(S)、亮度(V)3个颜色参量，还包括光强度(L)和光彩度(C)两个综合颜色度量指标[16]。其中光强度、光彩度的计算方法如式（1）、（2）所示。

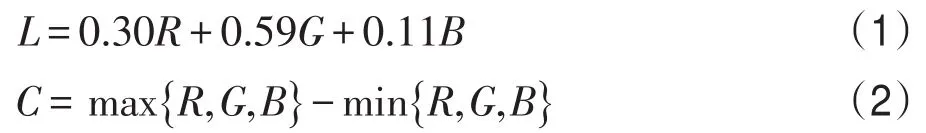
3.2美学度量

3.2.1Benford度量

Benford度量是图像颜色偏离Benford分布的统计度量[17]，量化指标记作BL。将灰度直方图按灰度级[0，255]等分成9个区间，统计每个区段实际直方图与Benford分布之间的差异diffi(i=1,2,…,9)：

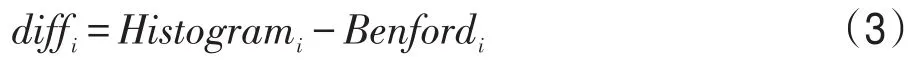
其中，Histogrami和Benfordi分别表示灰度直方图、Benford分布在对应区间上的频数。

Benford度量指标由式（4）确定：

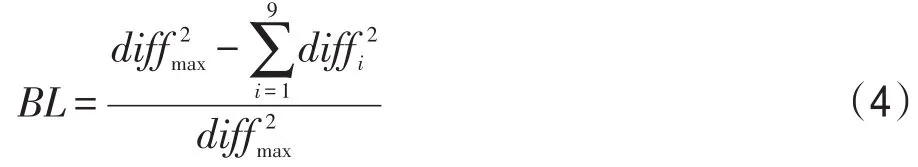
3.2.2分形维

分形维是图像上下文依赖不规则性的度量[18]，记作FD。Spehar等人的研究表明，图像分形维的最优峰值为1.35，过高分形维的图像略显复杂，过低分形维的图像呈现无趣[19]。本文首先采用盒维数（box counting）统计图像分形特征。设图像分形维数为dim，分形维量化指标的定义为：

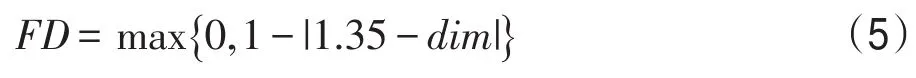
3.2.3全局对比因子

全局对比因子是图像在不同分辨率下的对比度，记作GCF。对比度低表明图像美学质量低。在不同分辨率下计算图像灰度强度对应的局部对比度Contrasti(i=1,2,…,9)，详细计算方法可以参考文献[20]。GCF的形式化定义为：

其中，wi(i=1,2,…,9)是对应局部对比度的权重因子，由i(-0.406 385i/9+0.334 573)/9+0.087 752 6所确定。

3.2.4Shannon熵

Shannon熵是图像不确定性的度量，熵越大，不确定性越大，信息量也越大[21-22]。将图像灰度直方图按照灰度级[0，255]等分成256个区间。图像美学Shannon熵记作SE，形式化的定义为：

其中，Histi是直方图上任意像素灰度落入第i个区间的概率。

3.2.5彩色度

彩色度是Hasler等人[23]提出的一个自然图像颜色评估指标，记作CF，计算公式如式（8）所示：

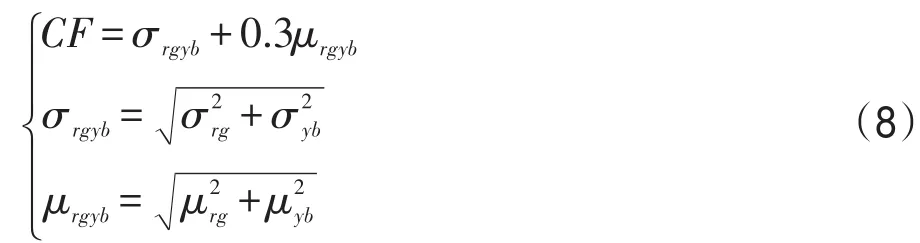
其中，μ和σ表示对应向量的均值和标准差；rg和yb表示以RGB颜色空间中的红R、绿G、蓝B分量为基础的过渡向量，具体计算如式（9）所示：

彩色度的定量指标按照7个等级分别对应了人眼的主观评价，彩色度量化结果与主观评价数据的互相关性约为95.3%[23]。

3.3调色板/主题色、色相环

主题色提取是一个相对成熟的课题，已有方法及其改进版众多，核心在于分析图像中主要的视觉色彩特征。Weeks等人提出的K-means方法因其简单快速而备受关注[24]，本文选用该方法形成部分代表性图像在RGB颜色空间的8种主题色。反之，在HSV颜色空间中，色调H是色彩的首要特征，是区分不同颜色的最准确标准，以0°～360°为取值范围，用角度度量色相所生成的图称为色相直方图、色相环或者色轮。Matusda等人研究了色彩和谐的色相分布模式[25-26]，并将其应用于与色彩设计相关的领域。本文以部分代表性静态沙画图像为例，统计色相环，并分析其分布的和谐模式匹配。

3.4数据场复杂度

前述美学指标对沙画图像复杂度的评价更侧重于宏观全局分析，对局部微观考虑得不多。数据场因其兼顾全局和局部数据空间认知而被广泛使用，本文建立图像数据场，提出了利用场的平均势值探索合适的美学分析指标[27]。将图像像素看成是数域空间的对象，利用数据场描述局部邻域像素之间的相互作用关系，充分发挥图像像素在灰度值空间上的全局认知能力，建立图像数据场，将图像灰度值空间映射到数据场的势值空间。具体方法为：对任意给定的灰度图像映射 g:[1 w]×[1 h]→{0,1,…,255}，h、w表示图像高度和宽度，g(x,y)表示位于(x,y)坐标处的像素灰度值，以k为模板半径（本文实验取2），计算中心像素和邻域的灰度差异，并视作图像数据场质点的质量m(i,j)=|g(i,j)-g(x,y)|，获得单个数据质点的势值。沙画图像的数据场复杂度用整个场中质点的平均势值进行量化，记为DFC，如式（10）所示：

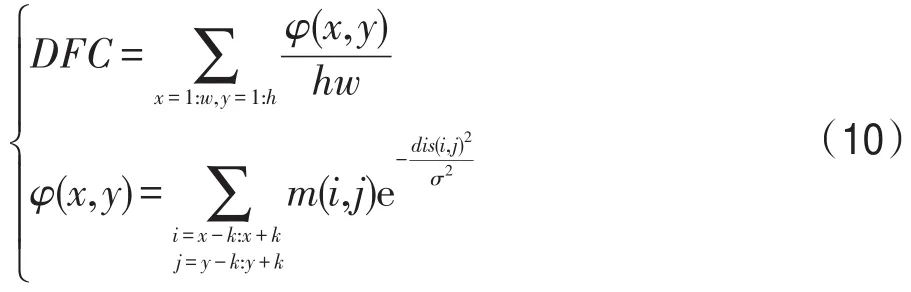
其中，dis(i,j)表示(x,y)中心和(i,j)邻域两者之间的距离；为数据场的影响因子。

4　沙画作品的量化分析

在Matlab2014b环境下，编程实现了相关功能，机器配置为i7 2.4 GHz CPU，8 GB内存。具体来源分布情况为：李韬沙画100幅，苏大宝沙画100幅，于云龙沙画100幅，尤佳沙画100幅，张铮铮沙画50幅，国内佚名沙画150幅，国外佚名沙画67幅，依次记为No1～No7。选择前7个沙画师作为代表的原因在于这些沙画师大多数享誉四方，自成一派。前3个是男沙画师。No1李韬是少数能登上人民大会堂的沙画艺术家之一，作品富于中国特色古风神韵的灵动（http://www.litaoshahua.com/index.html）。No2苏大宝被国内媒体誉为沙画第一人，曾获中国年度艺术人物等（http://www.sudabao.cn/index.html）。No3于云龙是国内第一个能使沙画在不同场景变换不同色彩的创作者，作品以中国文化为底蕴，中西绘画技法相结合（http://www.yunlongshahua.com/）。后两个是女沙画师。No4尤佳是中国最早从事沙画表演的女沙画艺术家之一，创立了喜沙沙沙画，作品细腻优雅而不失大气（http://www.xishasha.com/）。No5张铮铮师从中国动态沙画创始人高赞民，长于意境刻画与画面转承创意，扎根西部家乡并致力于沙画培训和推广（http://www.siyiwenhua.com/）。选择另外两类沙画旨在探索明星沙画师和佚名沙画师的创作差异，比较国内外大众沙画师的风格。

4.1量化指标统计与分析

4.1.1基本特征统计与分析

对于所有静态沙画图像，分别获取了其R、G、B值，并利用Matlab自带的rgb2hsv()函数提取了H、S、V分量值，也计算了各分量的最小值、最大值、均值、标准差等。为便于观察，将均值列在表1中。初步定量分析表明，No5张铮铮沙画中R、G、B最大值的均值最小，作品风格偏暗，H值的均值最小也支持了这一点。R、G、B标准差的均值最小，风格相对集中。

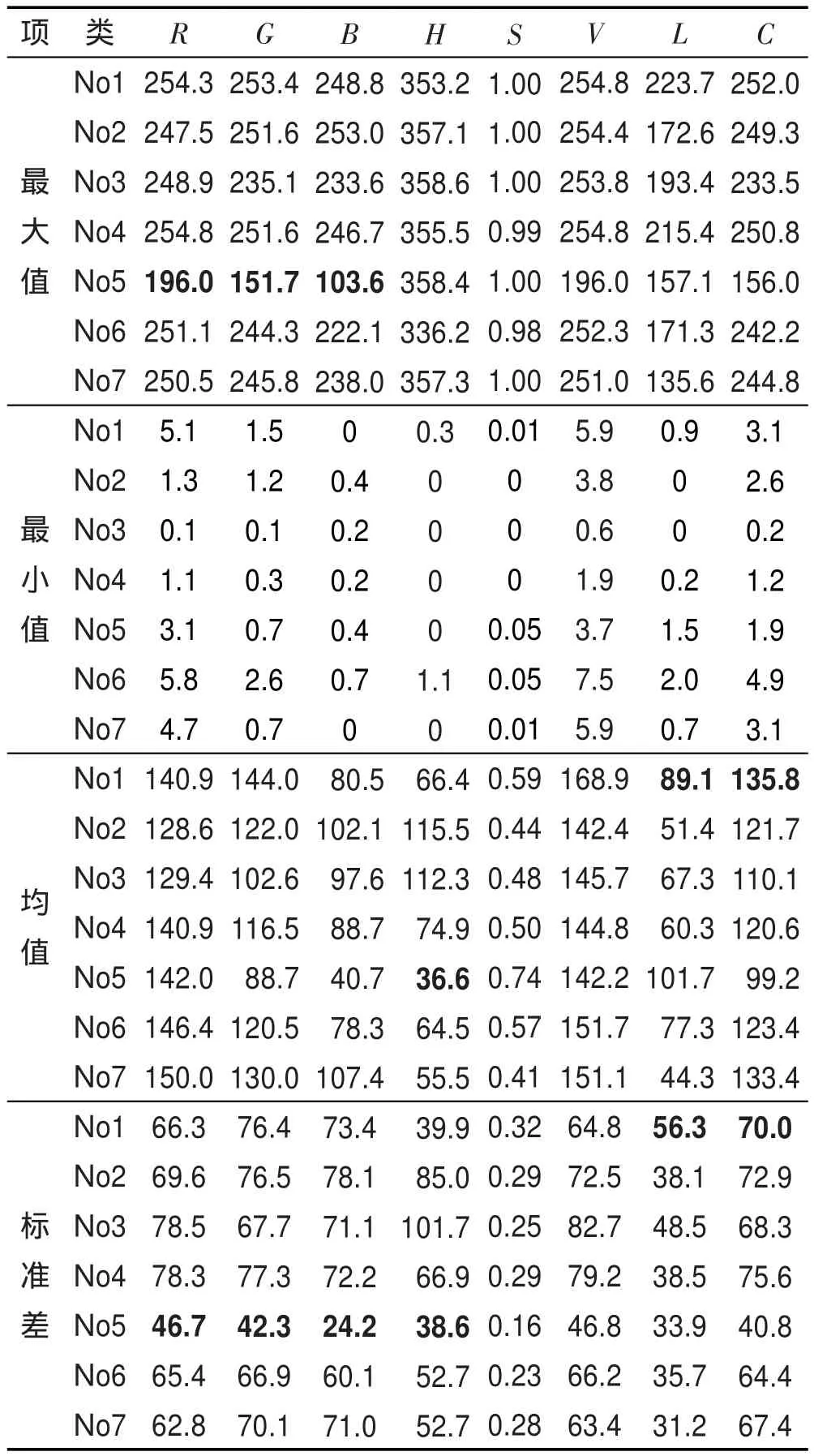
Table 1　Results of basic statistical characteristics表1　基本特征统计结果

进一步，对于每幅图像按照式（1）和（2）分别计算其光强度和光彩度，相关的统计结果也列在表1中。初步定量分析表明，No1中L和C均值的均值较大，标准差的均值也大，表明作品总体色彩丰富，但偏好不一。同时，将每幅图像L和C均值的联合分布绘制在图2中，并附上每类沙画风格的L、C极值对应图像。总体上，L反映了沙画的亮度情况，均值越大，图像整体光强越明亮；C反映了沙画的色彩差异，C均值越大，图像整体光彩差异越显著。

Fig.2　Joint distribution of luminance and chroma图2　光强度和光彩度联合分布图

从沙画风格看，大多数类别的沙画分散在整个分布图平面，仅有No5的作品聚集度较高，位于分布图的右下方。这表明虽然张铮铮算不上传统意义上的明星沙画师，但其沙画仍然具有独特鲜明的风格特点，画风大气明晰，色彩细腻流畅。此外，No1沙画散点分布偏右，L值大，作品明亮；No2、No4分布偏上，C值大，作品色彩差异强；反之，No3分布偏下，作品色彩流畅，过渡平稳。直观地对比图2附上的沙画图像也可以基本证实以上风格特点。No6、No7国内外佚名沙画作品分布极为离散，在光强度和光彩度上表现为风格迥异。

4.1.2Benford度量特征统计与分析

Benford度量反映了静态沙画图像各像素的灰度强度使用频率分布与Benford定律的吻合程度。BL量化的统计结果如图3所示，图中的柱形线表示平均指标值，垂直线刻画指标的波动范围，折线代表不同沙画师作品的指标变化趋势（下同）。No1的BL均值最大，波动较小，表明其沙画作品超出常规，人工精雕细琢。No5的BL均值最小，对应的沙画作品更符合Benford分布规律，中规中矩，不显山露水，也在一定程度上更验证了张铮铮沙画师一直所推崇的大众化路线。No3的BL值波动极小，均值较大，表明从Benford度量的角度，其沙画作品风格始终如一，且与李韬沙画一样长于意境雕琢。No6、No7的BL值波动范围极大，表明各个大众佚名沙画师在沙画灰度图像是否遵从Benford统计分布表现不一，在BL度量下也展示了这些沙画师创作上百花齐放的特点。

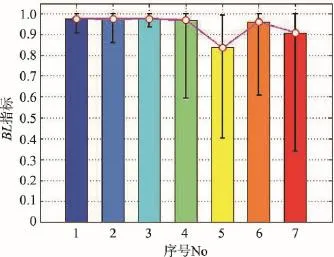
Fig.3　Results byBLindex图3　BL指标统计图

4.1.3分形维特征统计与分析

分形维度量反映了图像分形集的复杂程度。FD量化的统计结果如图4所示。No3的FD均值较小，表明其沙画作品超出常规，人工精雕细琢，事实上，评论也认为于云龙沙画作品雍容大器、气势磅礴。No5的FD值波动较小，表明其沙画作品的分形复杂性总体保持一致，与其他沙画师的大开大合风格明显不同。反之，No2、No4的FD值波动较大，表明苏大宝、尤佳这两个沙画师的作品分形复杂性不一致，风格多样化。

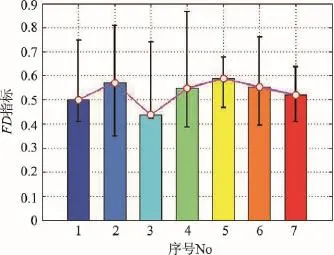
Fig.4　Results byFDindex图4　FD指标统计图

4.1.4全局对比因子特征统计与分析

全局对比因子反映了图像的综合差异变化情况。GCF量化的统计结果如图5所示。No4的GCF均值最大，波动也极大，表明尤佳单个沙画作品的画风变换丰富，但不同作品的风格不一。No5的GCF均值最小，表明张铮铮作品图像的平均变化度不高。总体上看，7类沙画图像的GCF值波动范围都比较大，表明沙画师都不拘泥于单一的差异变化度，喜好根据不同的主题和背景创作出或同、或异的沙画作品。

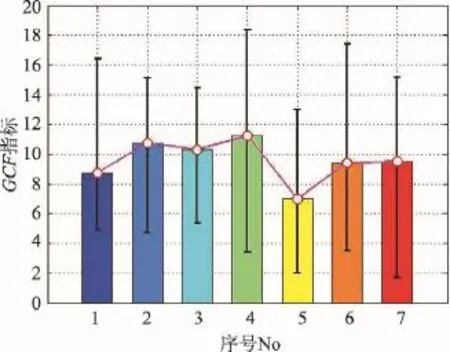
Fig.5　Results byGCFindex图5　GCF指标统计图

4.1.5Shannon熵特征统计与分析

Shannon熵反映了静态沙画图像的不确定性。SE量化的统计结果如图6所示。总体上看，No1～No4 共4类沙画图像的SE值波动范围相对较小，表明沙画师都保持较一致的沙子表现手法。No5的SE均值最小，表明张铮铮作品整体表现为沙子分布较离散，疏密相间，均匀不一。No4～No5女性沙画师作品SE均值更小，表明其表现手法细腻，更注重局部细节；反之，No1～No3这3位男性沙画师更注重大局，沙子分布更均匀，画风更大气。

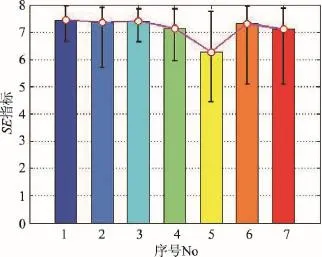
Fig.6　Results bySEindex图6　SE指标统计图

4.1.6彩色度特征统计与分析

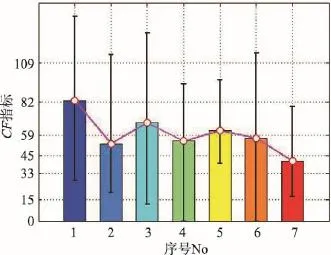
Fig.7　Results byCFindex图7　CF指标统计图

彩色度反映了沙画呈现的视觉色彩效果，主要由沙画的背景灯光和沙子的颜色所决定。CF量化的统计结果如图7所示。No1的CF均值约为82，色彩度高，但波动范围极大。No7的CF均值约为33，接近彩色度低的水平，表明这部分沙画样本更倾向于使用单一的背景灯光和沙子。其他类别CF均值都趋近于45～59，彩色度中等，也接近人类对客观世界的普适认知。总体上，7类沙画图像CF值波动范围都较大，表明即使是同一个沙画师的不同作品在背景灯光、沙子使用等方面仍然存在较大的差异。

4.2归一化统计与指标相关性分析

前述定量结果分析的是原始绝对数据，为了进一步深入剖析同一沙画师的不同沙画作品风格，不同沙画师的沙画作品创作在可计算美学框架下的指标度量，将前述所有数据按指标分别归一化到[0，1]区间，将绝对数据规范化为相对数据，具体归一化方法很多，本文使用Matlab自带的mapminmax()函数。归一化的统计结果如图8所示。对比图8和图3～图7可发现存在若干不同，原因在于未归一化的量化指标值波动范围大，波动幅度不一，归一化后更便于定量分析，具体表现为以下几点：

（1）从FD指标看，No2在分形维度量下趋于极端，大部分作品FD值在667幅沙画样本整体上为中等偏小，但非极小值，在表现风格上总体分形复杂性仍然较低。No4也是如此。

（2）从GCF指标看，No4在全局复杂因子量化下走向两个极端，且大部分作品GCF值中等偏小，但非极小值，总体全局差异性较低。

（3）从SE指标看，No4的大部分作品SE值中等偏小，但非极小值，总体趋于稳定，Shannon熵较低，用沙相对不均匀，更注重局部细节。同样，No5的作品整体SE值偏大，但也有较多极小值，在沙子的均匀性方面表现风格不稳定。

（4）从CF指标看，No2的CF均值最大，表明作品整体彩色度较高，但也有少量作品彩色度极低，导致在图8中展示了不高的CF均值。此外，No1在该项指标上的排名发生了较大的变化，主要是由于李韬沙画样本中包含两种不同背景灯光风格的作品，其中暖色背景导致CF值极大，冷色背景导致CF值极小。

（5）从No1～No5类沙画师的性别看，男沙画师的作品比女沙画师的作品获得了更高的平均量化指标值，特别在BL、GCF等指标上这种差异更加明显。表明男沙画师更擅长大手笔，女沙画师更专注局部细节。

（6）从No6、No7类国内外沙画作品看，与国外沙画师的作品相比，国内沙画师的作品在BL、GCF等指标上获得了更大的平均分值，反之，在FD、SE等指标上获得了更小的平均分值，在CF指标上获得了基本相近的平均分。表明国内佚名沙画师更擅长大手笔，但在彩色度上没有明显区别。事实上，国外沙画多注重情节，画面处理比较理性，有些作品画面极具连贯性，反之，国内沙画更注重意境，也很难被国外沙画师复制和理解。

（7）从图8指标排序的总体趋势上看，GCF、SE指标的统计值虽存在一定差异，但总体相关性更强。其次，BL值也更接近前述两个度量指标，这就反映了这些指标能够在某种意义上较全面地刻画静态沙画作品的若干共性，其排名的趋势差异也揭示了这些作品的不同特点。当然，FD、CF指标更是顺其自然地描述了这些作品的一些差异。

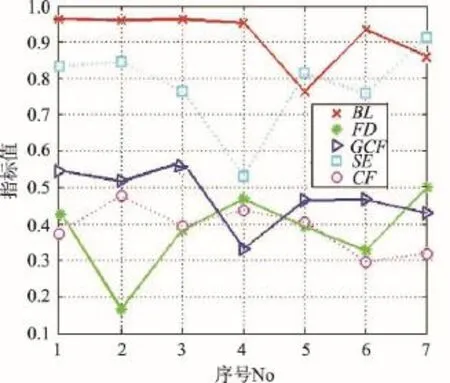
Fig.8　Results by normalized indexes图8　归一化的指标统计图

事实上，项目组经人工分类并总结分析后发现，沙画表演大致包含了洒、漏、擦、抹、划、勾等至少6种手势技法，所使用手的部位，包括手指的指尖、指甲、指腹等，手掌的掌心、掌根、掌被等，力度或轻或重，不同部位、不同力度产生不同尺度、不同类型的视觉复杂度。

为便于相关性分析，列出了统计指标排名，指标值越高，排名越靠后，分值越高，指标值最小，排名第一，记1分，依次类推。结果如表2所示，总分由高到低依次为No1、No2、No3、No7、No4、No5、No6。总体上看，排名越高意味着归一化指标的统计均值之和越大，越不符合Benford分布，分形复杂度越偏离最优值，沙画图像Shannon熵越大，全局差异对比性越强，主观彩色度越高。

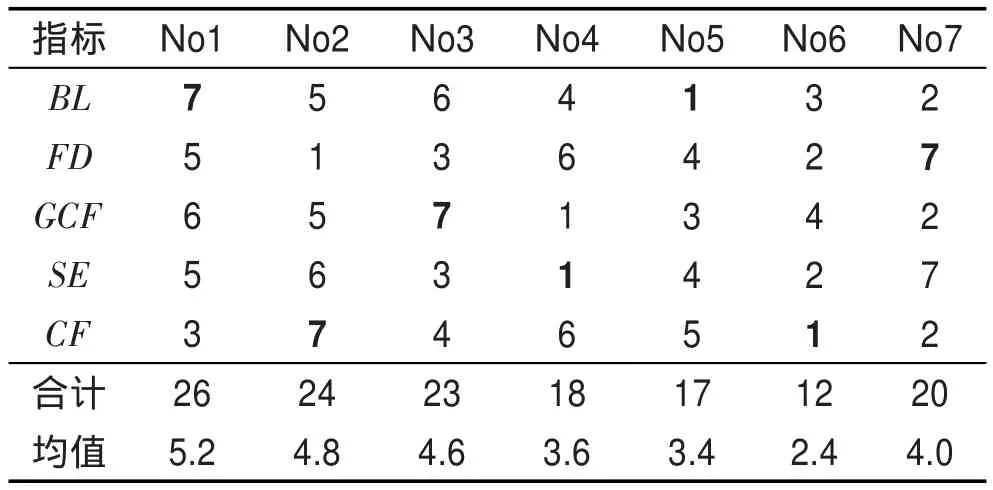
Table 2　Rank list by normalized indexes表2　归一化的统计指标排名

4.3数据场复杂度特征统计与分析

数据场复杂度反映了沙画视觉呈现的平均局部复杂性。归一化的DFC量化结果如图9所示，No1～No7 的DFC指标值排名由小到大分别为2，6，5，7，1，4，3，No5的DFC均值最小，作品的平均局部复杂度较低。总体上看，7类沙画图像的DFC值波动范围都比较大，表明沙画师都不拘泥于单一的局部复杂度，通常根据不同主题和背景创作出不同风格的作品。当然，更主要的原因还在于沙画表演过程中涉及众多手势技法，产生了不同的效果。总体上，实验验证了DFC指标具备一定可靠性，与图5中GCF指标排名趋势近似相同。

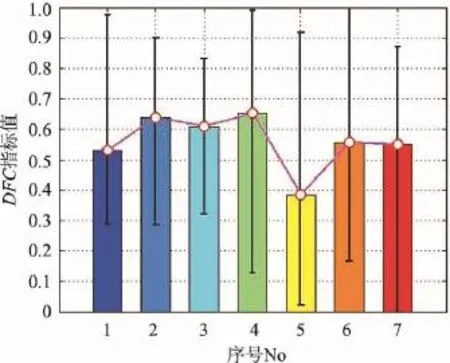
Fig.9　Results byDFCindex图9　DFC指标统计图

4.4纹理特征统计与分析

纹理表达指标有多种，与灰度共生矩阵等其他纹理统计方法相比较，Tamura方法对于纹理特征的表达在视觉上更有意义，广泛应用于图像检索、分析等领域，本文选用该方法进行纹理特征统计与分析实验。Tamura从心理学的角度研究表明[28]，人类视觉对于纹理的感知包含至少6个方面的分量，粗糙度（coarseness，SCrs）、对比度（contrast，SCon）、方向度（directionality，SDir）、线性度（linearity，SLin）、规整度（regularity，SReg）、粗略度（roughness，SRgh）等，其中前3个指标尤为重要，计算方法可参阅文献[28]，此处不再赘述。

本文计算了每幅沙画图像的纹理指标值，为便于分析，进行了归一化处理，并对每类沙画样本取均值，将各个纹理指标分组展示，实验结果如图10所示。纹理的粗糙度是反映纹理粒度的量，也是纹理度量最重要的指标之一。No1～No7的SCrs指标值排名由小到大分别为7，6，2，5，1，3，4，No5的SCrs均值最小，纹理重复次数较多；反之，No1的SCrs均值最大，反映其沙画纹理的基元尺寸较大。总体上，粗糙度SCrs越小，重复的纹理基元尺寸越小，次数越多，沙画作品的视觉效果越细腻。

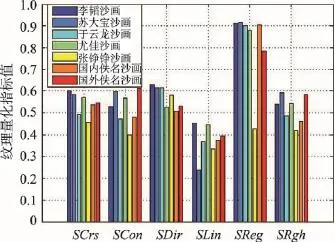
Fig.10　Results by texture index图10　纹理指标统计图

纹理的对比度由灰度级范围、直方图两极化程度、边缘锐度、重复模式周期等决定，No1～No7的SCon指标值排名由小到大分别为4，6，2，5，1，3，7。No7的对比度最高，表明国外沙画的灰度级范围广。

纹理的方向度描述了纹理区域的全局性度量，No1～No7的SDir指标值排名由小到大分别为7，6，5，2，4，1，3。总体上，方向度SDir由小到大依次对应了沙画纹理从没有方向到方向性较强，其中No1的方向度最高，条理性最强。

纹理的线性度是边缘方向角的平均共生程度，No1～No7的SLin指标值排名由小到大分别为7，1，3，6，2，4，5。总体上，沙画样本的线性度都比较低。

规整度SReg与局部窗口内粗糙度、对比度、方向度、线性度的标准差有关，No1～No7的SReg指标值排名由小到大分别为6，7，4，3，1，5，2。总体上，除张铮铮沙画外，其他样本的规整度都比较高。

粗略度SRgh是粗糙度和对比度的合成，No1～ No7的SRgh指标值排名由小到大分别为4，7，3，5，1，2，6，其中No2的SRgh均值最大，对应前述的粗糙度、对比度相对较高。

4.5主题色分析

为了充分反映沙画师的独特风格特点，在表2的基础上，选择了任意指标的归一化分值极值所对应的7幅沙画图像作为代表在后期进行主题色分析和色相分布和谐模式分析。在图11（a）所示沙画图像的基础上，从中分别提取了8个主题色，列在图11（b）中。No1的主题色以绿、黄色系为主，对应主观视觉发现，作品使用了绿色沙、暖光；No2的主题色以绿、白色系为主，作品使用了彩沙、冷光；No3的主题色以红色系为主，作品使用了普通沙、红光；No4～No7的主题色均以黄、黑色系为主，作品使用了普通沙、冷光。

从主题色的色系、色彩看，No1～No3前3类沙画的代表作品一般至少为3个色系，色彩也更丰富，导致图8中量化的CF均值较大也相对合理。反之，其余4类，特别是No5～No7，主题色明显更加单调，事实上，图8中这些沙画师对应的整体CF均值也比较小。

从这些代表沙画的主观视觉效果来看，No1李韬的代表沙画非常精致，除非人工精心搭配沙子，很难生成与之相同的艺术感染力，沙画图像与传统Benford分布偏差较大也在意料之中，无疑会导致BL指标值最大。反之，No5的代表沙画平淡、自然，于是该作品的BL值最小值。换句话就意味着，设定与BL值有关的适应度函数，通过计算机程序自动演化，也可能产生No5相似的视觉效果。No2的代表沙画包含了红、绿、蓝、黑、褐等多种颜色，画面色泽鲜艳，取得最大的CF值也比较合理。反之，No6的代表沙画基本上由厚厚的沙子堆积而成，更接近黑白沙画的视觉效果，在视觉上毫无色彩美感，因此其CF值最小。No3的代表沙画沙子疏密相间，粗中有细，变化自如，整体对比度极高，也就对应GCF值最大。No4的代表沙画沙子整体极其不均匀，但画风基本没有变化，局部相似性大，全局对比度低，因此该作品的SE值、GCF值均最小。No7的代表沙画画风自然理性，沙子的分布相对均匀，分形复杂度高，不规则性强，在所有沙画样本中FD值、SE值均最大。

事实上，项目组的总结分析表明，沙画背景灯光包括黑白、彩色、单色，其中单色又分为暖色（黄光为主）、冷色（白光为主），不同的背景灯光产生不同的视觉色彩冲击。同时，沙子质地包括普通沙、染色沙、烧结沙等，沙子的粗细有别，光学性质不同，沙子的颜色也有单色、彩色的差异，不同的沙子在相同的环境下也会照射出不同的艺术效果，反映到沙画图像上主题色的使用自然也不尽相同。例如，黄色系普通沙和红色系染色沙在黄色暖光背景下所产生的沙画效果具有鲜明的视觉差异。

总体来说，不同灯光背景、沙子质地，结合前述不同手势技法、手部使用等共同组合都会形成不同视觉艺术效果，也导致不同美学量化指标值。

4.6色相分布和谐模式与用色分析

在图11（a）所示沙画图像的基础上，分别提取了色彩和谐模式分布情况，如图11（c）所示。所谓色彩和谐就是自然连贯、完美无暇、赏心悦目的视觉感知，是一种主观感受的色彩平衡状态。在HSV颜色模式下，色彩和谐的第一要素通常是色相。因此，色相分布和谐模式是沙画图像的色彩搭配美学客观度量[25-26]。分布模式匹配的结果如表3所示，No5的代表沙画为i型，No3、No6为V型，No4、No7为L型，No1为Y型，No2为X型，和谐模式匹配程度越高，沙画色彩越和谐，反之，匹配程度相对更低者意味着色彩视觉冲击更强烈。

Fig.11　Typical sand image analysis图11　代表性静态沙画图像分析

Table 3　Harmonic template of typical images表3　代表性沙画图像的和谐模式类型

一般来说，互补色系能够构成较和谐的视觉效果，但单色系、临近色系及互补色系的组合也能获得较好的视觉美感。No5的代表沙画用色属于典型的单色系，作为舞台沙画表演，色彩组合略显单调。No3、No6的代表沙画属于临近色系，但用色相对较为平淡、均匀。No4、No7的代表沙画是组合L型，但均有少量颜色未被使用，匹配度不高，作品有待改善的空间较大。No1、No2的代表沙画均采用了互补色，但是No1的代表沙画在互补色系的两方呈现为不对称，No2的代表沙画在互补色系的两方相对更均匀。虽然二者的色相分布已经非常接近视觉设计领域惯用的互补型用色，但是互补的对称性均较弱，从色相和谐分布模式匹配的理论上说，也存在改进空间。

4.7讨论

总体上，本文方法对沙画作品的可计算美学分析是有效的。但是需要指出的是，可计算美学分析的性能显然和沙画作品库、美学指标数量等具有极其密切的关系。

一方面，以BL、FD、GCF、SE、CF、DFC为美学指标，考察指标个数依次为1～6个，随机选择1～6个指标，统计7类沙画的平均排名，并以表2的排名均值为期望，统计均方误差（mean squared error，MSE）。考虑到随机性，2～5个指标的实验共独立运行10次取平均值，实验结果如图12所示。随着指标数的增加，MSE逐渐减小，在指标数为5时出现拐点，原因在于统计的期望值以表2中5个指标的对应排名均值为准，事实上并非实际真实评价排名值（理想的真实值并不存在，毕竟主客观评价无法严格一一对应）。虽有一定影响，但图12仍能反应美学分析性能与指标数量的关系。理论上说，指标数越多，可计算美学分析的评价结果越准确，同时也会增加美学客观评价的时间耗费，一定程度上降低分析性能。

另一方面，考察了作品库数量与美学分析性能的关系。以667幅图像为原始作品库，依次取10%～ 90%共9个采样子库，从每类沙画中随机选择相应比例的沙画进行BL、FD、GCF、SE、CF、DFC等6个指标的量化分析，统计7类沙画在6个指标共同量化下的总排名，并以表2的排名合计为期望值，统计MSE。同样考虑到随机性，每次采样实验共独立运行10次取平均值，实验结果如图13所示，随着作品数的增加，MSE逐渐减小。换句话说，收集的每类沙画作品数量越多，美学量化评价结果越精确。但由于沙画作品的广泛收集尚存在困难，相对制约了所提出方法的分析性能。

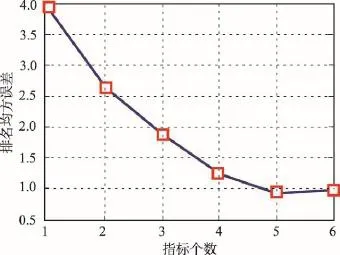
Fig.12　MSEof ranking at different number of indexes图12　排名均方误差随指标数的变化

Fig.13　MESof ranking sum at different sample ratio图13　排名和的均方误差随采样比的变化

5　结束语

本文在可计算美学的框架体系下，引入色彩模式、主题色、色相环、Benford度量、分形维、全局对比因子、Shannon熵、彩色度、数据场复杂度等量化的美学指标，选取李韬、苏大宝、于云龙、尤佳、张铮铮等5位中国代表性沙画师为研究对象，整理450幅静态沙画作品，辅以国内外佚名沙画师的217幅作品，对国内外沙画艺术的创作风格进行了量化统计与分析。结果表明，从前述美学指标的角度探索静态沙画图像的可计算美学分析是科学可行的，国内外沙画师在色彩运用、复杂度等方面存在较大差异，同类沙画师在表现手法和形式上既有区别也有联系，各个量化指标能较好地反映不同沙画作品中的美学特征，基本能与当前主流的主观评价相吻合。

当然，可计算美学分析和计算机沙画艺术尚属新兴课题，其研究任重而道远。下一步的工作主要可以从以下方面展开：一是扩大沙画作品库，引入更多更好的美学指标，继续探索静态沙画艺术创作的可计算美学分析，增强客观评价的鲁棒性和完备性，以期为沙画艺术创作风格的优劣评价、真伪鉴定等提供有意义的客观依据；二是开展沙画作品风格分类，以美学量化特征为基础，引入机器学习等方法建立合适的分类评价模型，探索计算机自学习、自演化机制，以期朝着使计算机具备拟人类（Baby-Like[29]）的视觉智能与审美感知方向努力；三是增加对沙画表演过程的关注，尝试构建计算机沙画艺术与沙画表演作品之间的量化桥梁，为计算机沙画艺术自动创作与表演提供有价值的参考和借鉴。

[1]Ura M,Yamada M,Endo M,et al.A paint tool for image generation of sand animation style[J].IEICE ITE Technical Report,2009,33(21):7-12.

[2]Kazi R H,Chua K C,Zhao Shengdong,et al.SandCanvas: a multi-touch art medium inspired by sand animation[C]// Proceedings of the 2011 SIGCHI Conference on Human Factors in Computing Systems,Vancouver,Canada,May 7-12,2011.New York,USA:ACM,2011:1283-1292.

[3]Lin C F,Fuh C S.Uncle sand:a sand drawing application in iPad[C]//Proceedings of the Computer Vision,Graphics, and Image Processing Conference,Nantou,China,Aug2012.

[4]Urbano P.The T.albipennis sand painting artists[C]//LNCS 6625:Proceedings of the 2011 International Conference on Applications of Evolutionary Computation,Torino,Italy, Apr 27-29,2011.Berlin,Heidelberg:Springer,2011:414-423.

[5]Song G,Yoon K H.Sand image replicating sand animation process[C]//Proceedings of the 19th Korea-Japan Joint Workshop on Frontiers of Computer Vision,Incheon,Korea, Jan 30-Feb 1,2013.Piscataway,USA:IEEE,2013:74-77.

[6]Taylor R P,Micolich A P,Jonas D.Fractal analysis of pollock’s drip paintings[J].Nature,1999,399:399-422.

[7]Li Congcong,Chen Tsuhan.Aesthetic visual quality assessment of paintings[J].IEEE Journal of Selected Topics in Signal Processing,2009,3(2):236-252.

[8]den Heijer E.Evolving symmetric and balanced art[C]// Studies in Computational Intelligence 577:Chapter of Computational Intelligence.Basel,Switzerland:Springer International Publishing,2015:33-47.

[9]Liu Xiaowei,Pu Yuanyuan,Huang Yaqun,et al.Quantitative statistics and analysis for painting visual art style[J]. Journal of Frontiers of Computer Science and Technology, 2013,7(10):942-952.

[10]Geng Weidong.The algorithms and principles of non-photorealistic graphics artistic rendering and cartoon animation[M]. Hangzhou:Zhejiang University Press&Springer,2009.

[11]Kyprianidis J E,Collomosse J,Wang Tinghuai,et al.State of the art:a taxonomy of artistic stylization techniques for images and video[J].IEEE Transactions on Visualization and Computer Graphics,2013,19(5):866-886.

[12]Qian Wenhua,Xu Dan,Yue Kun,et al.Rendering pyrography style painting based on deviation mapping[J].Journal of Image and Graphics,2013,18(7):836-843.

[13]Wang Weining,Yi Jingjian,He Qianhua.Review for computational image aesthetics[J].Journal of Image and Graphics, 2012,17(8):893-901.

[14]Wang Weining,Yi Jingjian,Xu Xiangmin,et al.Computational aesthetics of image classification and evaluation[J]. Journal of Computer-Aided Design and Computer Graphics, 2014,26(7):1075-1083.

[15]den Heijer E,Eiben A E.Evolving art using multiple aesthetic measures[C]//LNCS 6625:Proceedings of the 2011 International Conference on Applications of Evolutionary Computation,Torino,Italy,Apr 27-29,2011.Berlin,Heidelberg:Springer,2011:234-243.

[16]den Heijer E,Eiben A E.Investigating aesthetic measures for unsupervised evolutionary art[J].Swarm and Evolutionary Computation,2014,16:52-68.

[17]Jolion J M.Images and Benford’s law[J].Journal of Mathematical Imaging and Vision,2001,14(1):73-81.

[18]Wannarumon S,Bohez E L J,Annanon K.Aesthetic evolutionary algorithm for fractal-based user-centered jewelry design[J].Artificial Intelligence for Engineering Design,Analysis and Manufacturing,2008,22:19-39.

[19]Spehar B,Clifford C,Newell B,et al.Universal aesthetic of fractals[J].Computers and Graphics,2003,27(5):813-820.

[20]Matkovic K,Neumann L,Neumann A,et al.Global contrast factor—a new approach to image contrast[C]//Proceedings of the 1st Eurographics Conference on Computational Aesthetics in Graphics,Visualization and Imaging,Girona, Spain,May 18-20,2005.Aire-la-Ville,Switzerland:EurographicsAssociation,2005:159-168.

[21]Rigau J,Feixas M,Sbert M.Conceptualizing BirkhoffƳs aesthetic measure using Shannon entropy and Kolmogorov complexity[C]//Proceedings of the 3rd Eurographics Conference on Computational Aesthetics in Graphics,Visualization and Imaging,Banff,Canada,Jun 20-22,2007.Aire-la-Ville,Switzerland:EurographicsAssociation,2007:105-112. [22]Rigau J,Feixas M,Sbert M.Informational aesthetics measures[J].IEEE Computer Graphics and Applications,2008, 28(2):24-34.

[23]Hasler D,Süsstrunk S.Measuring colourfulness in natural images[J].Proceedings of the SPIE,2003,5007:87-95.

[24]Weeks A R,Hague G E.Color segmentation in the HSI color space using the K-means algorithm[J].Proceedings of the SPIE:Nonlinear Image Processing VIII,1997,3026:143-154.

[25]Tokumaru M,Muranaka N,Imanishi S.Color design support system considering color harmony[C]//Proceedings of the 2002 IEEE International Conference on Fuzzy Systems, Honolulu,USA,May 12-17,2002.Piscataway,USA:IEEE, 2002:378-383.

[26]Cohen-Or D,Sorkine O,Gal R,et al.Color harmonization[J]. ACM Transaction on Graphics,2006,25(3):624-630.

[27]Wu Tao,Qin Kun.Image data field for homogeneous region based segmentation[J].Computers and Electrical Engineering,2012,38(2):459-470.

[28]Hideyuki T,Shunji M,Takashi Y.Textural features corresponding to visual perception[J].IEEE Transactions on Systems,Man and Cybernetics,1978,8(6):460-473.

[29]Yan Shuicheng.Deep learning:AI to True-AI[EB/OL].Cnbeta[2015-10-09].http://cnbeta.com/view_433939.htm.

附中文参考文献：

[9]刘晓巍,普园媛,黄亚群,等.绘画视觉艺术风格的量化统计与分析[J].计算机科学与探索,2013,7(10):942-952.

[12]钱文华,徐丹,岳昆,等.偏离映射的烙画风格绘制[J].中国图象图形学报,2013,18(7):836-843.

[13]王伟凝,蚁静缄,贺前华.可计算图像美学研究进展[J].中国图象图形学报,2012,17(8):893-901.

[14]王伟凝,蚁静缄,徐向民,等.可计算的图像美学分类与评估[J].计算机辅助设计与图形学学报,2014,26(7):1075-1083.

[29]颜水成.深度学习:从AI到True-AI[EB/OL].Cnbeta[2015-10-09].http://cnbeta.com/view_433939.htm.

WU Tao was born in 1980.He received the Ph.D.degree in computer science and technology from Wuhan University in 2012.Now he is an associate professor at Lingnan Normal University,and the senior member of CCF.His research interests include digital sand painting,intelligent digital image processing and computer vision,etc.

吴涛（1980—），男，湖北汉川人，2012年于武汉大学获得工学博士学位，现为岭南师范学院副教授，CCF高级会员，主要研究领域为沙画数字化，智能图像处理，计算机视觉等。发表学术论文约50篇，主持国家自然科学基金项目、广东省高校优秀青年教师培养计划项目、教育部人文社会科学基金交叉项目、广东省自然科学基金项目等。

YANG Junjie was born in 1969.He received the Ph.D.degree in computer technology and applications from Huazhong University of Science and Technology in 2006.Now he is a professor at Lingnan Normal University.His research interests include digital art,E-learning and power dispatch automation,etc.

杨俊杰（1969—），男，湖北利川人，2006年于华中科技大学获得工学博士学位，现为岭南师范学院教授，主要研究领域为艺术数字化，数字化教育，电力调度自动化等。发表学术论文30余篇，主持国家自然科学基金重大项目、中国博士后科学基金项目等，2010年获教育部科技进步一等奖。

RAN Guohong was born in 1971.He received the M.S.degree in fine arts from Nanjing University of the Arts in 2010.Now he is an associate professor at Lingnan Normal University.His research interests include visual arts and oil painting,etc.

冉国洪（1971—），男，四川乐山人，2010年于南京艺术学院获得文学硕士学位，现为岭南师范学院副教授，清华大学高级访问学者，主要研究领域为视觉艺术，油画艺术等。发表学术论文10余篇。

ComputationalAestheticsAnalysis on Sand Painting Style*

WU Tao1+,YANG Junjie2,RAN Guohong3
1.School of Information Science and Technology,Lingnan Normal University,Zhanjiang,Guangdong 524048,China 2.Guangdong Engineering and Technological Development Center for E-learning,Zhanjiang,Guangdong 524048, China 3.Department of FineArts,Lingnan Normal University,Zhanjiang,Guangdong 524048,China +Corresponding author:E-mail:E-mail:taowu0706@gmail.com

Sand painting is a very new and popular performance art technique,and the researches on computer-aided sand painting are growing rapidly,but most of the current works seem to be biased.Various features,including color pattern,color theme,color wheel,Benford index,fractal dimension,global contrast factor,Shannon entropy,colorfulness,data field complexity and Tamura texture,are introduced into the framework of computational aesthetics, and several sand performers are involved into the numerical calculation and statistics of sand painting art style.Then the computational aesthetics analysis on sand images is achieved.The experimental results suggest that,the computeraided aesthetic evaluations can reflect the differences and similarities among the different types of sand images, which well correspond to human aesthetic perception,and as one of the useful bridge between sand painting art andcomputer-aided sand animation,the quantitative supplement is proposed for the subjective evaluation of sand painting art style,and then a reference is also provided for automatic creation of computer-aided sand animation.

art style;sand painting art;computational aesthetics;image statistics;image visualization

2015-10,Accepted 2016-02.

10.3778/j.issn.1673-9418.1510048

A

TP391

*The National Natural Science Foundation of China under Grant No.61402399(国家自然科学基金);the Foundation for Distinguished Young Teachers in Higher Education of Guangdong Province under Grant No.Yq2014117(广东省高等学校优秀青年教师培养计划项目).

CNKI网络优先出版:2016-03-07,http://www.cnki.net/kcms/detail/11.5602.tp.20160307.1710.002.html